Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T03:15:11.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Spanwise oscillatory wall motion in channel flow: drag-reduction mechanisms inferred from DNS-predicted phase-wise property variations at $\textit {Re}_{\boldsymbol {\boldsymbol{\tau}}} =1000$

Published online by Cambridge University Press:  10 March 2014

L. Agostini ,
E. Touber  and
M. A. Leschziner
L. Agostini*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
E. Touber
Affiliation:
Department of Mechanical Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
M. A. Leschziner
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A direct-numerical-simulation-based study is presented, which focuses on the response of near-wall turbulence and skin friction to the imposition of an oscillatory spanwise wall motion in channel flow. One point of contrast to earlier studies is the relatively high Reynolds number of the flow, namely 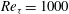$Re_\tau =1000$ in the unforced baseline flow. Another is the focus on transients in the drag that are in the form of moderate oscillatory variations in the skin friction and near-wall turbulence around the low-drag state at a sub-optimal actuation period. These conditions allow phase-averaged statistics to be extracted, during the periodic drag decrease and rise, that shed light on the interaction between turbulence and the unsteady Stokes strain. Results are presented for, among others, the phase-averaged second moments of stochastic fluctuations and their budgets, enstrophy components and joint probability density functions. The study identifies velocity skewness – the wall-normal derivative of the angle of the velocity vector – as playing a significant role in the streak-damping process during the drag-reduction phase. Furthermore, the phase-wise asymmetry in the skewness is identified as the source of a distinctive hysteresis in all properties, wherein the drag decrease progresses over a longer proportion of the actuation cycle than the drag increase. This feature, coupled with the fact that the streak-generation time scale limits the ability of the streaks to re-establish themselves during the low-skewness phase when the actuation period is sufficiently short, is proposed to drive the drag-reduction process. The observations in the study thus augment a previously identified mechanism proposed by two of the present authors, in which the drag-reduction process was linked to the rate of change in the Stokes strain in the upper region of the viscous sublayer where the streaks are strongest. Furthermore, an examination of the stochastic-stress budgets and the enstrophy lead to conclusions contrasting with those recently proposed by other authors, according to which the drag-reduction process is linked to increases in enstrophy and turbulence-energy dissipation. It is shown, both for the transient drag-reduction phase and the periodic drag fluctuations around the low-drag state, that the drag decrease/increase phases are correlated with decreases/increases in both enstrophy and dissipation.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulence control Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 606 - 635
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blesbois, O., Chernyshenko, S. I., Touber, E. & Leschziner, M. A. 2013 Pattern prediction by linear analysis of turbulent flow with drag reduction by wall oscillation. J. Fluid Mech. 724, 607–641.CrossRefGoogle Scholar
Choi, K. S. 2002 Near-wall structure of turbulent boundary layer with spanwise-wall oscillation. Phys. Fluids 14, 2530–2542.Google Scholar
Di Cicca, G. M., Iuso, G., Spazzini, P. G. & Onorato, M. 2002 Particle image velocimetry investigation of a turbulent boundary layer manipulated by spanwise wall oscillations. J. Fluid Mech. 467, 41–56.Google Scholar
Fishpool, G. M. & Leschziner, M. A. 2009 Stability bounds for explicit fractional-step schemes for the Navier–Stokes equations at high Reynolds number. Comput. Fluids 38, 1289–1298.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.Google Scholar
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., Yen, N.-C., Tung, C. C. & Liu, H. H. 1998 The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 454 (1971), 903–995.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Lardeau, S. & Leschziner, M. A. 2013 The streamwise drag-reduction response of a boundary layer subjected to a sudden imposition of transverse oscillatory wall motion. Phys. Fluids 25 (7), 075109.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $\mbox{Re}_\tau =590$ . Phys. Fluids 11 (4), 943–945.Google Scholar
Quadrio, M. & Ricco, P 2003 Initial response of a turbulent channel flow to spanwise oscillation of the walls. J. Turbul. 4 (7).Google Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.Google Scholar
Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.Google Scholar
Rhie, C. M. & Chow, W. L. 1983 Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 21 (11), 1525–1532.Google Scholar
Ricco, P. 2004 Modification of near-wall turbulence due to spanwise wall oscillations. J. Turbul. 5 (24).Google Scholar
Ricco, P., Ottonelli, C., Hasegawa, Y. & Quadrio, M. 2012 Changes in turbulent dissipation in a channel flow with oscillating walls. J. Fluid Mech. 700, 1–28.Google Scholar
Ricco, P. & Quadrio, M. 2008 Wall-oscillation conditions for drag reduction in turbulent channel flow. J. Heat Transfer Fluid Flow 29 (4), 891–902.Google Scholar
Skote, M. 2011 Turbulent boundary layer flow subject to streamwise oscillation of spanwise wall-velocity. Phys. Fluids 23, 081703.CrossRefGoogle Scholar
Skote, M. 2012 Temporal and spatial transients in turbulent boundary layer flow over an oscillating wall. J. Heat Transfer Fluid Flow 38, 1–12.Google Scholar
Skote, M. 2013 Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows. J. Fluid Mech. 730, 273–294.Google Scholar
Temmerman, L., Leschziner, M. A., Mellen, C. P. & Fröhlich, J. 2003 Investigation of wall-function approximations and subgrid-scale models in large eddy simulation of separated flow in a channel with streamwise periodic constrictions. Intl J. Heat Fluid Flow 24 (2), 157–180.Google Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.Google Scholar
Xu, C.-X. & Huang, W.-X. 2005 Transient response of Reynolds stress transport to spanwise wall oscillation in a turbulent channel flow. Phys. Fluids 17, 018101.Google Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 9 (12).Google Scholar