Published online by Cambridge University Press: 13 July 2021
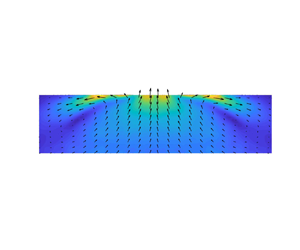
The aim of this paper is to experimentally and analytically study the solutocapillary flow induced in a waterbody due to the presence of a solute source on its surface and the mixing induced by this flow of the solutes and gases dissolved at and near the surface into the waterbody. According to the analytic solution, the induced flow is analogous to a doublet flow in the sense that the flow is directed towards (or away from) the source within a conical region with its vertex at the source, and outside the conical region, the flow is away from (or towards) the source. Our particle image velocimetry and planar laser-induced fluorescence data show that the actual flow is far more complex than the analytic solution because of the influence of other factors which are not accounted for in the analytic model. There is an approximate agreement, but only for the intermediate distances from the source needle. In experiments, the flow changes direction into the waterbody when the solute-induced surface tension gradient driving the flow becomes comparable to the surface tension gradients on the surface due to factors such as contamination and temperature gradients. This causes the mixing of gases dissolved near the surface into the waterbody. Also, as the solute gradient at the surface gives rise to the force that drives the flow, when the solute diffusion coefficient is smaller the flow persists longer because the gradient is maintained for a longer distance.