Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T13:50:47.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Sloshing in a Hele-Shaw cell: experiments and theory

Published online by Cambridge University Press:  13 October 2017

Francesco Viola ,
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]  and
Benjamin Dollet Open the ORCID record for Benjamin Dollet [Opens in a new window]
Francesco Viola
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
François Gallaire
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
Benjamin Dollet
Affiliation:
Institut de Physique de Rennes, UMR 6251 CNRS and Université Rennes 1, Campus Beaulieu, Bâtiment 11A, 35042 Rennes CEDEX, France
Get access Rights & Permissions [Opens in a new window]

Abstract

The response of the free liquid surface in a Hele-Shaw cell subjected to a horizontal oscillation is investigated. We study the low-oscillation-amplitude regime and we show, by varying the fluid viscosity, $\unicode[STIX]{x1D708}$, and the forcing frequency, 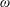$\unicode[STIX]{x1D714}$, that the ratio between the Stokes viscous length, 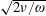$\sqrt{2\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$, and the cell thickness greatly affects the amplitude and phase lag of the gravity waves. In particular, the sloshing system undergoes an underdamped/overdamped transition for sufficiently large viscosities. A consistent theoretical model, based on a modification of Darcy’s law to include unsteadiness, is then introduced to rationalize the experimental observations. Contrary to traditional sloshing wave theory, the viscous flow dissipation comes at leading order in the analysis, rather than as a higher-order asymptotic correction to the inviscid sloshing dynamics. The analytical expression for the resonance curves agrees well with experimental results without tunable parameters.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bensimon, D., Kadanoff, L. P., Liang, S., Shraiman, B. I. & Tang, C. 1986 Viscous flows in two dimensions. Rev. Mod. Phys. 58 (4), 977–999.Google Scholar
Cantat, I. 2013 Liquid meniscus friction on a wet plate: bubbles, lamellae, and foams. Phys. Fluids 25 (3), 031303.Google Scholar
Cocciaro, B., Faetti, S. & Nobili, M. 1991 Capillarity effects on surface gravity waves in a cylindrical container: wetting boundary conditions. J. Fluid Mech. 231, 325–343.CrossRefGoogle Scholar
Davies, J. T. & Vose, R. W. 1965 On the damping of capillary waves by surface films. Proc. R. Soc. Lond. A 286 (1405), 218–234.Google Scholar
Dwyer, H. & Erickson, D. 1969 Hele-shaw and porous medium flow for space fuel systems. In 2nd Fluid and Plasma Dynamics Conference, AIAA Paper No. 69-678, http://dx.doi.org/10.2514/6.1969-678.Google Scholar
Faltinsen, O. M. & Timokha, A. N. 2009 Sloshing. Cambridge University Press.Google Scholar
Gondret, P. & Rabaud, M. 1997 Shear instability of two-fluid parallel flow in a Hele-Shaw cell. Phys. Fluids 9 (11), 3267–3274.Google Scholar
Ibrahim, R. A. 2005 Liquid Sloshing Dynamics: Theory and Applications. Cambridge University Press.Google Scholar
Ibrahim, R. A., Pilipchuk, V. N. & Ikeda, T. 2001 Recent advances in liquid sloshing dynamics. Appl. Mech. Rev. 54, 133–199.Google Scholar
Kalogirou, A., Moulopoulou, E. E. & Bokhove, O. 2016 Variational finite element methods for waves in a Hele-Shaw tank. Appl. Math. Model. 40 (17), 7493–7503.CrossRefGoogle Scholar
Keulegan, G. H. 1959 Energy dissipation in standing waves in rectangular basins. J. Fluid Mech. 6 (01), 33–50.Google Scholar
Mayer, H. C. & Krechetnikov, R. 2012 Walking with coffee: why does it spill? Phys. Rev. E 85, 046117.Google Scholar
Miles, J. M. 1967 Surface-wave damping in closed basins. Proc. R. Soc. Lond. A 297 (1451), 459–475.Google Scholar
Plouraboué, F. & Hinch, E. J. 2002 Kelvin–Helmholtz instability in a Hele-Shaw cell. Phys. Fluids 14 (3), 922–929.CrossRefGoogle Scholar
Royon-Lebeaud, A., Hopfinger, E. & Cartellier, A. 2007 Liquid sloshing and wave breaking in cylindrical and square-base containers. J. Fluid Mech. 577, 467–494.CrossRefGoogle Scholar
Ruyer-Quil, C. 2001 Inertial corrections to the Darcy law in a Hele-Shaw cell. C. R. Acad. Sci. Paris II 329 (5), 337–342.Google Scholar
Saffman, P. G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Sauret, A., Boulogne, F., Cappello, J. D., Dressaire, E. & Stone, H. A. 2015 Damping of liquid sloshing by foams. Phys. Fluids 27 (2), 022103.Google Scholar
Veldman, A. E. P., Gerrits, J., Luppes, R., Helder, J. A. & Vreeburg, J. P. B. 2007 The numerical simulation of liquid sloshing on board spacecraft. J. Comput. Phys. 224, 82–99.Google Scholar
Viola, F., Brun, P. T., Dollet, B. & Gallaire, F. 2016 Foam on troubled water: capillary induced finite-time arrest of sloshing waves. Phys. Fluids 28, 091701.Google Scholar
Womersley, J. R. 1955 Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 127 (3), 553.Google Scholar