Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T11:29:23.807Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple and practical model for combined wave–current canopy flows

Published online by Cambridge University Press:  24 February 2015

Robert B. Zeller ,
Francisco J. Zarama ,
Joel S. Weitzman  and
Jeffrey R. Koseff
Robert B. Zeller*
Affiliation:
Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Francisco J. Zarama
Affiliation:
Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Joel S. Weitzman
Affiliation:
Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
Jeffrey R. Koseff
Affiliation:
Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Laboratory experiments were used to evaluate and improve modelling of combined wave–current flow through submerged aquatic canopies. Horizontal in-canopy particle image velocimetry (PIV) and wavemaker-measurement synchronization allowed direct volume averaging and ensemble averaging by wave phase, which were used to fully resolve the volume-averaged unsteady momentum budget. Parameterizations for the drag, Reynolds stress, vertical advection, wake production and shear production were tested against the laboratory measurements. The drag was found to have small errors due to unsteadiness and the finite aspect ratio of the canopy elements. The Smagorinsky model for the Reynolds stress showed much better agreement with the measurements than the quadratic friction parameterization used in the literature. A proposed parameterization for the vertical advection based on linear wave theory was also found to be effective and is much more computationally efficient than solving the pressure Poisson equation. A simple 1D 0-equation Reynolds-averaged Navier–Stokes (RANS) model was developed to use these parameterizations. The basic framework of the model is an extrapolation from previous 2- and 3-box models to 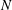$N$ boxes. While the resolution of the model is flexible, the filter length for the Smagorinsky parameterization has to be chosen appropriately. With the proper filter length, the 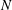$N$-box model demonstrated good agreement with the measurements at both low and high resolution. Scaling analysis was used to establish a region of parameter space where the 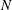$N$-box model is expected to be effective. The following conditions define this region: the wave-induced velocity is of similar or greater magnitude than the background current, the drag to shear length ratio is small enough to produce canopy behaviour, the wave orbital excursion is not much larger than the drag length, the Froude number is small and the canopy is under shallow submergence, yet far from emergent. Under these assumptions, the dominant balance is between pressure and unsteadiness, the drag is secondary, and the other terms are small. The simple Reynolds stress parameterization in the 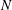$N$-box model is appropriate under these conditions because the Reynolds stress is unlikely to be the dominant source of error. This finding is important because the Reynolds stress is typically one of the dominant drivers of computational cost and model complexity. Based on these findings, the 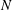$N$-box model is expected to be a practical tool for a wide range of combined wave–current canopy flows because of its simplicity and computational efficiency.

JFM classification

Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 842 - 880
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belcher, S. E., Harman, I. N. & Finnigan, J. J. 2012 The wind in the willows: flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 44, 479–504.CrossRefGoogle Scholar
Bradley, K. & Houser, C. 2009 Relative velocity of seagrass blades: implications for wave attenuation in low-energy environments. J. Geophys. Res. 114, F1.Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22 (1), 015110.CrossRefGoogle Scholar
Dalrymple, R. A. & Dean, R. G. 1991 Water Wave Mechanics for Engineers and Scientists. Prentice-Hall.Google Scholar
Falter, J. L., Atkinson, M. J. & Merrifield, M. A. 2004 Mass-transfer limitation of nutrient uptake by a wave-dominated reef flat community. Limnol. Oceanogr. 49 (5), 1820–1831.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Ghisalberti, M. 2009 Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61.Google Scholar
Ghisalberti, M. & Schlosser, T. 2013 Vortex generation in oscillatory canopy flow. J. Geophys. Res. 118 (3), 1534–1542.CrossRefGoogle Scholar
Grimmond, C. S. B. & Oke, T. R. 1999 Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 38 (9), 1262–1292.Google Scholar
Hansen, J. C. R. & Reidenbach, M. A. 2011 Wave and tidally driven flows in eelgrass beds and their effect on sediment suspension. Mar. Ecol. Prog. Ser. 448, 271–287.Google Scholar
Hu, Z., Suzuki, T., Zitman, T., Uittewaal, W. & Stive, M. 2014 Laboratory study on wave dissipation by vegetation in combined current–wave flow. Coast. Engng 88, 131–142.Google Scholar
King, A. T., Tinoco, R. O. & Cowen, E. A. 2012 A $k{-}{\it\varepsilon}$ turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 701, 1–39.CrossRefGoogle Scholar
Li, C. W. & Yan, K. 2007 Numerical investigation of wave–current–vegetation interaction. ASCE J. Hydraul. Engng 133 (7), 794–803.CrossRefGoogle Scholar
López, F. & García, M. 1998 Open-channel flow through simulated vegetation: suspended sediment transport modeling. Water Resour. Res. 34 (9), 2341–2352.Google Scholar
Lowe, R. J., Falter, J. L., Koseff, J. R., Monismith, S. G. & Atkinson, M. J. 2007 Spectral wave flow attenuation within submerged canopies: implications for wave energy dissipation. J. Geophys. Res. 112, C5.Google Scholar
Lowe, R. J., Koseff, J. R. & Monismith, S. G. 2005 Oscillatory flow through submerged canopies, part 1: velocity structure. J. Geophys. Res. 110, C10.Google Scholar
Lowe, R. J., Shavit, U., Falter, J. L., Koseff, J. R. & Monismith, S. G. 2008 Modeling flow in coral communities with and without waves: a synthesis of porous media and canopy flow approaches. Limnol. Oceanogr. 53 (6), 2668–2680.Google Scholar
Luhar, M., Coutu, S., Infantes, E., Fox, S. & Nepf, H. 2010 Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. 115, C12.Google Scholar
Luhar, M., Infantes, E., Orfila, A., Terrados, J. & Nepf, H. M. 2013 Field observations of wave-induced streaming through a submerged seagrass (Posidonia oceanica) meadow. J. Geophys. Res. 118 (4), 1955–1968.CrossRefGoogle Scholar
Marshall, P. A. 2000 Skeletal damage in reef corals: relating resistance to colony morphology. Mar. Ecol. Prog. Ser. 200, 177–189.Google Scholar
Maza, M., Lara, J. L. & Losada, I. J. 2013 A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast. Engng 80, 16–34.Google Scholar
Moltchanov, S., Bohbot-Raviv, Y. & Shavit, U. 2011 Dispersive stresses at the canopy upstream edge. Boundary–Layer Meteorol. 139 (2), 333–351.CrossRefGoogle Scholar
Monismith, S. G. 2007 Hydrodynamics of coral reefs. Annu. Rev. Fluid Mech. 39, 37–55.Google Scholar
Narasimhamurthy, V. D. & Andersson, H. I. 2009 Numerical simulation of the turbulent wake behind a normal flat plate. Intl J. Heat Fluid Flow 30 (6), 1037–1043.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Neumeier, U. & Ciavola, P. 2004 Flow resistance and associated sedimentary processes in a Spartina maritima salt-marsh. J. Coast. Res. 20 (2), 435–447.Google Scholar
Orth, R. J., Carruthers, T. J. B., Dennison, W. C., Duarte, C. M., Fourqurean, J. W., Heck, K. L., Hughes, A. R., Kendrick, G. A., Kenworthy, W. J., Olyarnik, S., Short, F. T., Waycott, M. & Williams, S. L. 2006 A global crisis for seagrass ecosystems. Bioscience 56 (12), 987–996.CrossRefGoogle Scholar
Philips, D. A., Rossi, R. & Iaccarino, G. 2013 Large-eddy simulation of passive scalar dispersion in an urban-like canopy. J. Fluid Mech. 723, 404–428.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pujol, D. & Nepf, H. 2012 Breaker-generated turbulence in and above a seagrass meadow. Cont. Shelf Res. 49, 1–9.Google Scholar
Pujol, D., Serra, T., Colomer, J. & Casamitjana, X. 2013 Flow structure in canopy models dominated by progressive waves. J. Hydrol. 486, 281–292.Google Scholar
Reidenbach, M. A., Koseff, J. R., Monismith, S. G., Steinbuck, J. V. & Genin, A. 2006 The effects of waves and morphology on mass transfer within branched reef corals. Limnol. Oceanogr. 51 (2), 1134–1141.Google Scholar
Ringuette, M. J.2004 Vortex formation and drag on low aspect ratio, normal flat plates. PhD thesis, California Institute of Technology.Google Scholar
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.Google Scholar
Stevens, A. W. & Lacy, J. R. 2012 The influence of wave energy and sediment transport on seagrass distribution. Estuar. Coast. 35 (1), 92–108.Google Scholar
Storlazzi, C. D., Brown, E. K., Field, M. E., Rodgers, K. & Jokiel, P. L. 2005 A model for wave control on coral breakage and species distribution in the Hawaiian Islands. Coral Reefs 24 (1), 43–55.CrossRefGoogle Scholar
Taebi, S., Lowe, R. J., Pattiaratchi, C. B., Ivey, G. N., Symonds, G. & Brinkman, R. 2011 Nearshore circulation in a tropical fringing reef system. J. Geophys. Res. 116, C2.Google Scholar
Tanino, Y. & Nepf, H. M. 2008 Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Engng 134 (1), 34–41.Google Scholar
Vreman, B., Geurts, B. & Kuerten, H. 1997 Large-eddy simulation of the turbulent mixing layer. J. Fluid Mech. 339, 357–390.Google Scholar
Ward, L. G., Kemp, W. M. & Boynton, W. R. 1984 The influence of waves and seagrass communities on suspended particulates in an estuarine embayment. Mar. Geol. 59 (1), 85–103.CrossRefGoogle Scholar
Waycott, M., Duarte, C. M., Carruthers, T. J. B., Orth, R. J., Dennison, W. C., Olyarnik, S., Calladine, A., Fourqurean, J. W., Heck, K. L., Hughes, A. R., Kendrick, G. A., Kenworthy, W. J., Short, F. T. & Williams, S. L. 2009 Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl Acad. Sci. USA 106 (30), 12377–12381.Google Scholar
Weitzman, J. S.2013 Current-and wave-driven flow and nutrient exchange in natural and model submerged vegetated canopies. PhD thesis, Stanford University.Google Scholar
Weitzman, J. S., Aveni-Deforge, K., Koseff, J. R. & Thomas, F. I. M. 2013 Uptake of dissolved inorganic nitrogen by shallow seagrass communities exposed to wave-driven unsteady flow. Mar. Ecol. Prog. Ser. 475, 65–83.Google Scholar
Weitzman, J. S., Zeller, R. B., Thomas, F. I. M. & Koseff, J. R. 2015 The attenuation of current- and wave-driven flow within submerged multispecific vegetative canopies. Limnol. Oceanogr. (submitted).CrossRefGoogle Scholar
Whittlesey, R. W., Liska, S. & Dabiri, J. O. 2010 Fish schooling as a basis for vertical axis wind turbine farm design. Bioinspir. Biomim. 5 (3), 035005.Google Scholar
Zeller, R. B., Weitzman, J. S., Abbett, M. E., Zarama, F. J., Fringer, O. B. & Koseff, J. R. 2014 Improved parameterization of seagrass blade dynamics and wave attenuation based on numerical and laboratory experiments. Limnol. Oceanogr. 59, 251–266.Google Scholar