Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhang, Wei
and
Wei, Mingjun
2017.
Model order reduction using DMD modes and adjoint DMD modes.
Bistrian, Diana Alina
and
Navon, Ionel Michael
2017.
Randomized dynamic mode decomposition for nonintrusive reduced order modelling.
International Journal for Numerical Methods in Engineering,
Vol. 112,
Issue. 1,
p.
3.
Stankiewicz, Witold
Morzyński, Marek
Kotecki, Krzysztof
and
Noack, Bernd R.
2017.
On the need of mode interpolation for data-driven Galerkin models of a transient flow around a sphere.
Theoretical and Computational Fluid Dynamics,
Vol. 31,
Issue. 2,
p.
111.
Taira, Kunihiko
Brunton, Steven L.
Dawson, Scott T. M.
Rowley, Clarence W.
Colonius, Tim
McKeon, Beverley J.
Schmidt, Oliver T.
Gordeyev, Stanislav
Theofilis, Vassilios
and
Ukeiley, Lawrence S.
2017.
Modal Analysis of Fluid Flows: An Overview.
AIAA Journal,
Vol. 55,
Issue. 12,
p.
4013.
Kou, Jiaqing
Zhang, Weiwei
Liu, Yilang
and
Li, Xintao
2017.
The lowest Reynolds number of vortex-induced vibrations.
Physics of Fluids,
Vol. 29,
Issue. 4,
Loiseau, Jean-Christophe
and
Brunton, Steven L.
2018.
Constrained sparse Galerkin regression.
Journal of Fluid Mechanics,
Vol. 838,
Issue. ,
p.
42.
Clainche, Soledad Le
Pérez, José M
and
Vega, José M
2018.
Spatio-temporal flow structures in the three-dimensional wake of a circular cylinder.
Fluid Dynamics Research,
Vol. 50,
Issue. 5,
p.
051406.
Kou, Jiaqing
Le Clainche, Soledad
and
Zhang, Weiwei
2018.
A reduced-order model for compressible flows with buffeting condition using higher order dynamic mode decomposition with a mode selection criterion.
Physics of Fluids,
Vol. 30,
Issue. 1,
Wang, Z.
Xiao, D.
Fang, F.
Govindan, R.
Pain, C. C.
and
Guo, Y.
2018.
Model identification of reduced order fluid dynamics systems using deep learning.
International Journal for Numerical Methods in Fluids,
Vol. 86,
Issue. 4,
p.
255.
Towne, Aaron
Schmidt, Oliver T.
and
Colonius, Tim
2018.
Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
821.
2018.
Data-Driven Sparse Sensor Placement for Reconstruction: Demonstrating the Benefits of Exploiting Known Patterns.
IEEE Control Systems,
Vol. 38,
Issue. 3,
p.
63.
Shaqarin, T
Noack, B R
and
Morzyński, M
2018.
The need for prediction in feedback control of a mixing layer.
Fluid Dynamics Research,
Vol. 50,
Issue. 6,
p.
065514.
Xie, Xuping
Bao, Feng
and
Webster, Clayton G.
2018.
Evolve Filter Stabilization Reduced-Order Model for Stochastic Burgers Equation.
Fluids,
Vol. 3,
Issue. 4,
p.
84.
Zhang, Meihua
and
Zheng, Zhongquan C.
2018.
Relations of POD modes and Lyapunov exponents to the nonlinear dynamic states in flow over oscillating tandem cylinders.
Physics of Fluids,
Vol. 30,
Issue. 12,
p.
123602.
Bistrian, D. A.
and
Navon, I. M.
2018.
Efficiency of randomised dynamic mode decomposition for reduced order modelling.
International Journal of Computational Fluid Dynamics,
Vol. 32,
Issue. 2-3,
p.
88.
Yu, Ming
Huang, Wei-Xi
and
Xu, Chun-Xiao
2019.
Data-driven construction of a reduced-order model for supersonic boundary layer transition.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
1096.
Zhao, Yijia
Zhao, Ming
Li, Xiaojian
Liu, Zhengxian
and
Du, Juan
2019.
A modified proper orthogonal decomposition method for flow dynamic analysis.
Computers & Fluids,
Vol. 182,
Issue. ,
p.
28.
Lu, Weiyu
Huang, Guoping
Wang, Jinchun
and
Hong, Shuli
2019.
Spatio–temporal dynamic mode decomposition in a shear layer flow.
Aerospace Science and Technology,
Vol. 91,
Issue. ,
p.
263.
Yu, Jian
Yan, Chao
and
Guo, Mengwu
2019.
Non-intrusive reduced-order modeling for fluid problems: A brief review.
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering,
Vol. 233,
Issue. 16,
p.
5896.
Mendez, M. A.
Balabane, M.
and
Buchlin, J.-M.
2019.
Multi-scale proper orthogonal decomposition of complex fluid flows.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
988.
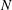 $N$th mode is defined recursively in an analogous manner based on the residual of an expansion using the first
$N$th mode is defined recursively in an analogous manner based on the residual of an expansion using the first 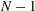 $N-1$ modes. The resulting recursive DMD (RDMD) modes are orthogonal by construction, retain pure frequency content and aim at low residual. Recursive DMD is applied to transient cylinder wake data and is benchmarked against POD and optimized DMD (Chen et al., J. Nonlinear Sci., vol. 22, 2012, pp. 887–915) for the same snapshot sequence. Unlike POD modes, RDMD structures are shown to have purer frequency content while retaining a residual of comparable order to POD. In contrast to DMD, with exponentially growing or decaying oscillatory amplitudes, RDMD clearly identifies initial, maximum and final fluctuation levels. Intriguingly, RDMD outperforms both POD and DMD in the limit-cycle resolution from the same snapshots. Robustness of these observations is demonstrated for other parameters of the cylinder wake and for a more complex wake behind three rotating cylinders. Recursive DMD is proposed as an attractive alternative to POD and DMD for empirical Galerkin models, in particular for nonlinear transient dynamics.
$N-1$ modes. The resulting recursive DMD (RDMD) modes are orthogonal by construction, retain pure frequency content and aim at low residual. Recursive DMD is applied to transient cylinder wake data and is benchmarked against POD and optimized DMD (Chen et al., J. Nonlinear Sci., vol. 22, 2012, pp. 887–915) for the same snapshot sequence. Unlike POD modes, RDMD structures are shown to have purer frequency content while retaining a residual of comparable order to POD. In contrast to DMD, with exponentially growing or decaying oscillatory amplitudes, RDMD clearly identifies initial, maximum and final fluctuation levels. Intriguingly, RDMD outperforms both POD and DMD in the limit-cycle resolution from the same snapshots. Robustness of these observations is demonstrated for other parameters of the cylinder wake and for a more complex wake behind three rotating cylinders. Recursive DMD is proposed as an attractive alternative to POD and DMD for empirical Galerkin models, in particular for nonlinear transient dynamics.