Published online by Cambridge University Press: 14 May 2019
We present a numerical study of quasistatic magnetoconvection in a cubic Rayleigh–Bénard (RB) convection cell subjected to a vertical external magnetic field. For moderate values of the Hartmann number  $Ha$ (characterising the strength of the stabilising Lorentz force), we find an enhancement of heat transport (as characterised by the Nusselt number
$Ha$ (characterising the strength of the stabilising Lorentz force), we find an enhancement of heat transport (as characterised by the Nusselt number 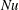 $Nu$). Furthermore, a maximum heat transport enhancement is observed at certain optimal
$Nu$). Furthermore, a maximum heat transport enhancement is observed at certain optimal 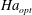 $Ha_{opt}$. The enhanced heat transport may be understood as a result of the increased coherence of the thermal plumes, which are elementary heat carriers of the system. To our knowledge this is the first time that a heat transfer enhancement by the stabilising Lorentz force in quasistatic magnetoconvection has been observed. We further found that the optimal enhancement may be understood in terms of the crossing of the thermal and the momentum boundary layers (BL) and the fact that temperature fluctuations are maximum near the position where the BLs cross. These findings demonstrate that the heat transport enhancement phenomenon in the quasistatic magnetoconvection system belongs to the same universality class of stabilising–destabilising (S–D) turbulent flows as the systems of confined Rayleigh–Bénard (CRB), rotating Rayleigh–Bénard (RRB) and double-diffusive convection (DDC). This is further supported by the findings that the heat transport, boundary layer ratio and temperature fluctuations in magnetoconvection at the boundary layer crossing point are similar to the other three cases. A second type of boundary layer crossing is also observed in this work. In the limit of
$Ha_{opt}$. The enhanced heat transport may be understood as a result of the increased coherence of the thermal plumes, which are elementary heat carriers of the system. To our knowledge this is the first time that a heat transfer enhancement by the stabilising Lorentz force in quasistatic magnetoconvection has been observed. We further found that the optimal enhancement may be understood in terms of the crossing of the thermal and the momentum boundary layers (BL) and the fact that temperature fluctuations are maximum near the position where the BLs cross. These findings demonstrate that the heat transport enhancement phenomenon in the quasistatic magnetoconvection system belongs to the same universality class of stabilising–destabilising (S–D) turbulent flows as the systems of confined Rayleigh–Bénard (CRB), rotating Rayleigh–Bénard (RRB) and double-diffusive convection (DDC). This is further supported by the findings that the heat transport, boundary layer ratio and temperature fluctuations in magnetoconvection at the boundary layer crossing point are similar to the other three cases. A second type of boundary layer crossing is also observed in this work. In the limit of 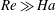 $Re\gg Ha$, the (traditionally defined) viscous boundary
$Re\gg Ha$, the (traditionally defined) viscous boundary 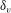 $\unicode[STIX]{x1D6FF}_{v}$ is found to follow a Prandtl–Blasius-type scaling with the Reynolds number
$\unicode[STIX]{x1D6FF}_{v}$ is found to follow a Prandtl–Blasius-type scaling with the Reynolds number 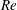 $Re$ and is independent of
$Re$ and is independent of 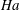 $Ha$. In the other limit of
$Ha$. In the other limit of 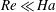 $Re\ll Ha$,
$Re\ll Ha$, 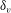 $\unicode[STIX]{x1D6FF}_{v}$ exhibits an approximate
$\unicode[STIX]{x1D6FF}_{v}$ exhibits an approximate 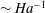 ${\sim}Ha^{-1}$ dependence, which has been predicted for a Hartmann boundary layer. Assuming the inertial term in the momentum equation is balanced by both the viscous and Lorentz terms, we derived an expression
${\sim}Ha^{-1}$ dependence, which has been predicted for a Hartmann boundary layer. Assuming the inertial term in the momentum equation is balanced by both the viscous and Lorentz terms, we derived an expression 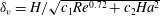 $\unicode[STIX]{x1D6FF}_{v}=H/\sqrt{c_{1}Re^{0.72}+c_{2}Ha^{2}}$ (where
$\unicode[STIX]{x1D6FF}_{v}=H/\sqrt{c_{1}Re^{0.72}+c_{2}Ha^{2}}$ (where 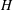 $H$ is the height of the cell) for all values of
$H$ is the height of the cell) for all values of 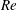 $Re$ and
$Re$ and 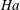 $Ha$, which fits the obtained viscous boundary layer well.
$Ha$, which fits the obtained viscous boundary layer well.