Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-10T05:42:30.824Z Has data issue: false hasContentIssue false
  • English
  • Français

A physical model of turbulence cascade via vortex reconnection sequence and avalanche

Published online by Cambridge University Press:  28 November 2019

Jie Yao Open the ORCID record for Jie Yao [Opens in a new window]  and
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]
Jie Yao
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Fazle Hussain*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

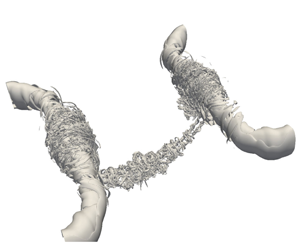
Viscous anti-parallel vortex reconnection is studied by means of direct numerical simulation for vortex Reynolds numbers $Re$ ($\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708}$, circulation/viscosity) up to 40 000. To suppress the inherent symmetry breaking due to the Kelvin–Helmholtz (planar jet) instability, as prevalent in prior studies, and to better explore the progression of the mechanism details, the simulation is performed by imposing symmetry and using double-precision arithmetic. We show, for the first time, the evidence of vortex reconnection cascade scenario initially proposed by Melander and Hussain (CTR Report, 1988), who suggested that the remnant threads, following the first reconnection, undergo successive reconnections in a cascade. Secondary reconnection (the details distinctly captured and visualized at a lower $Re=9000$) leads to the successive generation of numerous small-scale structures, including vortex rings, hairpin-like vortex packets and vortex tangles. As $Re$ increases, the third and higher generations of reconnection form a turbulent cloud avalanche consisting of a tangle of fine vortices. The energy is rapidly transferred to finer scales during reconnection, and a distinct - 5/3 inertial range is observed for the kinetic energy spectrum, associated with numerous resulting fine-scale bridgelets and thread filaments. In addition, we also discover an inverse cascade at large scales through the accumulation of bridgelets. The separation distance $\unicode[STIX]{x1D6FF}(t)$ before the first reconnection is found to scale as $t^{3/4}$, which is different from the typical 1/2 scaling for classical and quantum vortex filament reconnections. Both peak enstrophy and its production rate grow with $Re$ faster than the power law suggested by Hussain and Duraisamy (Phys. Fluids, vol. 23, 2011, 021701). Our simulations not only reveal the detailed mechanisms of high-$Re$ reconnection, but also shed light on the physics of turbulence cascade and present the reconnection avalanche as a realistic physical model for turbulence cascade.

JFM classification

Turbulent Flows: Turbulence theory Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A51
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archer, P. J., Thomas, T. G. & Coleman, G. N. 2008 Direct numerical simulation of vortex ring evolution from the laminar to the early turbulent regime. J. Fluid Mech. 598, 201–226.CrossRefGoogle Scholar
Ashurst, W. T. & Meiron, D. I. 1987 Numerical study of vortex reconnection. Phys. Rev. Lett. 58 (16), 1632–1635.CrossRefGoogle ScholarPubMed
Baggaley, A. W., Sherwin, L. K., Barenghi, C. F. & Sergeev, Y. A. 2012 Thermally and mechanically driven quantum turbulence in helium ii. Phys. Rev. B 86 (10), 104501.CrossRefGoogle Scholar
Bake, S., Meyer, D. G. W. & Rist, U. 2002 Turbulence mechanism in Klebanoff transition: a quantitative comparison of experiment and direct numerical simulation. J. Fluid Mech. 459, 217–243.CrossRefGoogle Scholar
Balakrishnan, S. K., Thomas, T. G. & Coleman, G. N. 2011 Oblique interaction of a laminar vortex ring with a non-deformable free surface: vortex reconnection and breakdown. J. Phys.: Conf. Ser. 318, 062002.Google Scholar
Beale, J. T., Kato, T. & Majda, A. 1984 Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Commun. Math. Phys. 94 (1), 61–66.CrossRefGoogle Scholar
Beardsell, G., Dufresne, L. & Dumas, G. 2016 Investigation of the viscous reconnection phenomenon of two vortex tubes through spectral simulations. Phys. Fluids 28 (9), 095103.CrossRefGoogle Scholar
Bermejo-Moreno, I., Pullin, D. I. & Horiuti, K. 2009 Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence. J. Fluid Mech. 620, 121–166.CrossRefGoogle Scholar
Bewley, G. P., Paoletti, M. S., Sreenivasan, K. R. & Lathrop, D. P. 2008 Characterization of reconnecting vortices in superfluid helium. Proc. Natl Acad. Sci. USA 105 (37), 13707–13710.CrossRefGoogle ScholarPubMed
Boratav, O. N., Pelz, R. B. & Zabusky, N. J. 1992 Reconnection in orthogonally interacting vortex tubes: Direct numerical simulations and quantifications. Phys. Fluids A 4 (3), 581–605.CrossRefGoogle Scholar
Brenner, M. P., Hormoz, S. & Pumir, A. 2016 Potential singularity mechanism for the Euler equations. Phys. Rev. Fluids 1 (8), 084503.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Lim, T. T. 2016 Evolution of an elliptic vortex ring in a viscous fluid. Phys. Fluids 28 (3), 037104.Google Scholar
Constantin, P., Fefferman, C. & Majda, A. J. 1996 Geometric constraints on potentially singular solutions for the 3-D Euler equations. Commun. Part. Diff. Equ. 21 (3–4), 559–571.Google Scholar
Davidson, P. A., Morishita, K. & Kaneda, Y. 2008 On the generation and flux of enstrophy in isotropic turbulence. J. Turbul. 9, N42.CrossRefGoogle Scholar
Doan, N. A. K., Swaminathan, N., Davidson, P. A. & Tanahashi, M. 2018 Scale locality of the energy cascade using real space quantities. Phys. Rev. Fluids 3 (8), 084601.CrossRefGoogle Scholar
Doering, C. R. 2009 The 3d Navier–Stokes problem. Annu. Rev. Fluid Mech. 41, 109–128.CrossRefGoogle Scholar
Domaradzki, J. A. & Carati, D. 2007 An analysis of the energy transfer and the locality of nonlinear interactions in turbulence. Phys. Fluids 19 (8), 085112.Google Scholar
Domaradzki, J. A. & Rogallo, R. S. 1990 Local energy transfer and nonlocal interactions in homogeneous, isotropic turbulence. Phys. Fluids A 2 (3), 413–426.CrossRefGoogle Scholar
Fonda, E., Sreenivasan, K. R. & Lathrop, D. P. 2019 Reconnection scaling in quantum fluids. Proc. Natl Acad. Sci. USA 116 (6), 1924–1928.CrossRefGoogle ScholarPubMed
Frisch, U. 1995 Turbulence: the Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.CrossRefGoogle Scholar
Goto, S., Saito, Y. & Kawahara, G. 2017 Hierarchy of antiparallel vortex tubes in spatially periodic turbulence at high Reynolds numbers. Phys. Rev. Fluids 2 (6), 064603.CrossRefGoogle Scholar
Horiuti, K. & Fujisawa, T. 2008 The multi-mode stretched spiral vortex in homogeneous isotropic turbulence. J. Fluid Mech. 595, 341–366.CrossRefGoogle Scholar
Horiuti, K. & Takagi, Y. 2005 Identification method for vortex sheet structures in turbulent flows. Phys. Fluids 17 (12), 121703.CrossRefGoogle Scholar
Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3-D incompressible Euler equations. J. Nonlinear Sci. 16 (6), 639–664.CrossRefGoogle Scholar
Howe, M. S. 2003 Theory of Vortex Sound, vol. 33. Cambridge University Press.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23 (2), 021701.CrossRefGoogle Scholar
Hussain, F. & Stout, E. 2013 Self-limiting and regenerative dynamics of perturbation growth on a vortex column. J. Fluid Mech. 718, 39–88.CrossRefGoogle Scholar
Jaque, R. S. & Fuentes, O. V. 2017 Reconnection of orthogonal cylindrical vortices. Eur. J. Mech. (B/Fluids) 62, 51–56.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kambe, T. & Minota, T. 1981 Sound radiation from vortex systems. J. Sound Vib. 74 (1), 61–72.CrossRefGoogle Scholar
Kerr, R. M. 1993 Evidence for a singularity of the three-dimensional, incompressible Euler equations. Phys. Fluids A 5 (7), 1725–1746.CrossRefGoogle Scholar
Kerr, R. M. 2013a Bounds for Euler from vorticity moments and line divergence. J. Fluid Mech. 729, R2.CrossRefGoogle Scholar
Kerr, R. M. 2013b Swirling, turbulent vortex rings formed from a chain reaction of reconnection events. Phys. Fluids 25 (6), 065101.CrossRefGoogle Scholar
Kerr, R. M. 2018 Enstrophy and circulation scaling for Navier–Stokes reconnection. J. Fluid Mech. 839, R2.CrossRefGoogle Scholar
Kerr, R. M. & Hussain, F. 1989 Simulation of vortex reconnection. Physica D 37 (1), 474–484.CrossRefGoogle Scholar
Kida, S. & Takaoka, M. 1994 Vortex reconnection. Annu. Rev. Fluid Mech. 26 (1), 169–177.CrossRefGoogle Scholar
Kida, S., Takaoka, M. & Hussain, F. 1991 Collision of two vortex rings. J. Fluid Mech. 230, 583–646.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2014 Reconnection of skewed vortices. J. Fluid Mech. 751, 329–345.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2018 A tent model of vortex reconnection under Biot–Savart evolution. J. Fluid Mech. 834, R1.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–306.Google Scholar
Koplik, J. & Levine, H. 1993 Vortex reconnection in superfluid helium. Phys. Rev. Lett. 71 (9), 1375.CrossRefGoogle ScholarPubMed
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.CrossRefGoogle Scholar
Li, N. & Laizet, S. 2010 2DECOMP & FFT – a highly scalable 2D decomposition library and FFT interface. In Cray User Group 2010 Conference, Edinburgh, Scotland, pp. 1–13.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25 (12), 2193–2203.CrossRefGoogle Scholar
Mao, X. & Hussain, F. 2017 Optimal transient growth on a vortex ring and its transition via cascade of ringlets. J. Fluid Mech. 832, 269–286.CrossRefGoogle Scholar
McGavin, P. & Pontin, D. I. 2018 Vortex line topology during vortex tube reconnection. Phys. Rev. Fluids 3 (5), 054701.CrossRefGoogle Scholar
McKeown, R., Ostilla-Mónico, R., Pumir, A., Brenner, M. P. & Rubinstein, S. M. 2018 Cascade leading to the emergence of small structures in vortex ring collisions. Phys. Rev. Fluids 3 (12), 124702.Google Scholar
Melander, M. V. & Hussain, F. 1988 Cut-and-connect of two antiparallel vortex tubes. In Studying Turbulence Using Numerical Simulation Databases, 2, pp. 257–286. Center for Turbulence Research.Google Scholar
Melander, M. V. & Hussain, F. 1993 Coupling between a coherent structure and fine-scale turbulence. Phys. Rev. E 48 (4), 2669.Google ScholarPubMed
Melander, M. V. & Hussain, F. 1994 Core dynamics on a vortex column. Fluid Dyn. Res. 13 (1), 1–37.CrossRefGoogle Scholar
Melander, M. V. & Zabusky, N. J. 1988 Interaction and apparent reconnection of 3d vortex tubes via direct numerical simulations. Fluid Dyn. Res. 3 (1–4), 247–250.Google Scholar
Moffatt, H. K. 2000 The interaction of skewed vortex pairs: a model for blow-up of the Navier–Stokes equations. J. Fluid Mech. 409, 51–68.CrossRefGoogle Scholar
Moffatt, H. K. & Kimura, Y. 2019a Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion. J. Fluid Mech. 870, R1.CrossRefGoogle Scholar
Moffatt, H. K. & Kimura, Y. 2019b Towards a finite-time singularity of the Navier–Stokes equations. Part 1. Derivation and analysis of dynamical system. J. Fluid Mech. 861, 930–967.CrossRefGoogle Scholar
Möhring, W. 1978 On vortex sound at low Mach number. J. Fluid Mech. 85 (4), 685–691.CrossRefGoogle Scholar
Ni, Q., Hussain, F., Wang, J. & Chen, S. 2012 Analysis of Reynolds number scaling for viscous vortex reconnection. Phys. Fluids 24 (10), 105102.CrossRefGoogle Scholar
Obukhov, A. M. 1941 On the distribution of energy in the spectrum of turbulent flow. Bull. Acad. Sci. USSR Geog. Geophys. 5, 453–466.Google Scholar
Orlandi, P., Pirozzoli, S. & Carnevale, G. F. 2012 Vortex events in Euler and Navier–Stokes simulations with smooth initial conditions. J. Fluid Mech. 690, 288–320.CrossRefGoogle Scholar
Pradeep, D. S. & Hussain, F. 2004 Effects of boundary condition in numerical simulations of vortex dynamics. J. Fluid Mech. 516, 115–124.CrossRefGoogle Scholar
Pradeep, D. S. & Hussain, F. 2010 Vortex dynamics of turbulence–coherent structure interaction. Theor. Comput. Fluid Dyn. 24 (1-4), 265–282.CrossRefGoogle Scholar
Pumir, A. & Kerr, R. M. 1987 Numerical simulation of interacting vortex tubes. Phys. Rev. Lett. 58 (16), 1636.CrossRefGoogle ScholarPubMed
van Rees, W. M., Hussain, F. & Koumoutsakos, P. 2012 Vortex tube reconnection at Re  = 104. Phys. Fluids 24 (7), 075105.CrossRefGoogle Scholar
Rorai, C., Skipper, J., Kerr, R. M. & Sreenivasan, K. R. 2016 Approach and separation of quantised vortices with balanced cores. J. Fluid Mech. 808, 641–667.CrossRefGoogle Scholar
Saffman, P. G. 1990 A model of vortex reconnection. J. Fluid Mech. 212, 395–402.CrossRefGoogle Scholar
Shelley, M. J., Meiron, D. I. & Orszag, S. A. 1993 Dynamical aspects of vortex reconnection of perturbed anti-parallel vortex tubes. J. Fluid Mech. 246, 613–652.CrossRefGoogle Scholar
Siggia, E. D. 1985 Collapse and amplification of a vortex filament. Phys. Fluids 28 (3), 794–805.CrossRefGoogle Scholar
Stanaway, S., Shariff, K. & Hussain, F. 1988 Head-on collision of viscous vortex rings. In Studying Turbulence Using Numerical Simulation Databases-I1, pp. 287–309. Center for Turbulence Research.Google Scholar
Taylor, G. I. & Green, A. E. 1937 Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. A 158 (895), 499–521.Google Scholar
Van Rees, W. M., Leonard, A., Pullin, D. I. & Koumoutsakos, P. 2011 A comparison of vortex and pseudo-spectral methods for the simulation of periodic vortical flows at high Reynolds numbers. J. Comput. Phys. 230 (8), 2794–2805.CrossRefGoogle Scholar
Villois, A., Proment, D. & Krstulovic, G. 2017 Universal and nonuniversal aspects of vortex reconnections in superfluids. Phys. Rev. Fluids 2 (4), 044701.CrossRefGoogle Scholar
Virk, D., Hussain, F. & Kerr, R. M. 1995 Compressible vortex reconnection. J. Fluid Mech. 304, 47–86.CrossRefGoogle Scholar
Wu, J.-Z. 2017 Vortex definition and vortex criteria. Sci. China Phys. Mech. Astron. 61 (2), 024731.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1980 Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 101 (03), 449–491.CrossRefGoogle Scholar
Zhao, Y., Yang, Y. & Chen, S. 2016 Vortex reconnection in the late transition in channel flow. J. Fluid Mech. 802, R4.CrossRefGoogle Scholar
Zuccher, S., Caliari, M., Baggaley, A. W. & Barenghi, C. F. 2012 Quantum vortex reconnections. Phys. Fluids 24 (12), 125108.CrossRefGoogle Scholar

Yao and Hussain supplementary movie 1

Time evolution of vorticity magnitude isosurfaces at 40% of maximum initial vorticity (shaded with contours of axial vorticity) for vortex reconnection at Re = 9000.

Download Yao and Hussain supplementary movie 1(Video)
Video 1.4 MB

Yao and Hussain supplementary movie 2

Time evolution of λ_2 isosurfaces of for vortex reconnection at Re = 9000.

Download Yao and Hussain supplementary movie 2(Video)
Video 1.3 MB

Yao and Hussain supplementary movie 3

Time evolution of λ_2 isosurfaces of for vortex reconnection at Re = 20 000.

Download Yao and Hussain supplementary movie 3(Video)
Video 3.6 MB

Yao and Hussain supplementary movie 4

Time evolution of λ_2 isosurfaces of for vortex reconnection at Re = 40 000.

Download Yao and Hussain supplementary movie 4(Video)
Video 1 MB