Published online by Cambridge University Press: 11 July 2017
An elegant model for passive scalar mixing and decay was given by Kraichnan (Phys. Fluids, vol. 11, 1968, pp. 945–953) assuming the velocity to be delta correlated in time. For realistic random flows this assumption becomes invalid. We generalize the Kraichnan model to include the effects of a finite correlation time,  $\unicode[STIX]{x1D70F}$, using renewing flows. The generalized evolution equation for the three-dimensional (3-D) passive scalar spectrum
$\unicode[STIX]{x1D70F}$, using renewing flows. The generalized evolution equation for the three-dimensional (3-D) passive scalar spectrum 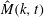 $\hat{M}(k,t)$ or its correlation function
$\hat{M}(k,t)$ or its correlation function 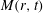 $M(r,t)$, gives the Kraichnan equation when
$M(r,t)$, gives the Kraichnan equation when 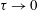 $\unicode[STIX]{x1D70F}\rightarrow 0$, and extends it to the next order in
$\unicode[STIX]{x1D70F}\rightarrow 0$, and extends it to the next order in  $\unicode[STIX]{x1D70F}$. It involves third- and fourth-order derivatives of
$\unicode[STIX]{x1D70F}$. It involves third- and fourth-order derivatives of 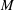 $M$ or
$M$ or 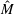 $\hat{M}$ (in the high
$\hat{M}$ (in the high 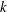 $k$ limit). For small-
$k$ limit). For small- $\unicode[STIX]{x1D70F}$ (or small Kubo number), it can be recast using the Landau–Lifshitz approach to one with at most second derivatives of
$\unicode[STIX]{x1D70F}$ (or small Kubo number), it can be recast using the Landau–Lifshitz approach to one with at most second derivatives of 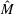 $\hat{M}$. We present both a scaling solution to this equation neglecting diffusion and a more exact solution including diffusive effects. To leading order in
$\hat{M}$. We present both a scaling solution to this equation neglecting diffusion and a more exact solution including diffusive effects. To leading order in  $\unicode[STIX]{x1D70F}$, we first show that the steady state 1-D passive scalar spectrum, preserves the Batchelor (J. Fluid Mech., vol. 5, 1959, pp. 113–133) form,
$\unicode[STIX]{x1D70F}$, we first show that the steady state 1-D passive scalar spectrum, preserves the Batchelor (J. Fluid Mech., vol. 5, 1959, pp. 113–133) form, 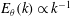 $E_{\unicode[STIX]{x1D703}}(k)\propto k^{-1}$, in the viscous–convective limit, independent of
$E_{\unicode[STIX]{x1D703}}(k)\propto k^{-1}$, in the viscous–convective limit, independent of  $\unicode[STIX]{x1D70F}$. This result can also be obtained in a general manner using Lagrangian methods. Interestingly, in the absence of sources, when passive scalar fluctuations decay, we show that the spectrum in the Batchelor regime at late times is of the form
$\unicode[STIX]{x1D70F}$. This result can also be obtained in a general manner using Lagrangian methods. Interestingly, in the absence of sources, when passive scalar fluctuations decay, we show that the spectrum in the Batchelor regime at late times is of the form 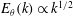 $E_{\unicode[STIX]{x1D703}}(k)\propto k^{1/2}$ and also independent of
$E_{\unicode[STIX]{x1D703}}(k)\propto k^{1/2}$ and also independent of  $\unicode[STIX]{x1D70F}$. More generally, finite
$\unicode[STIX]{x1D70F}$. More generally, finite  $\unicode[STIX]{x1D70F}$ does not qualitatively change the shape of the spectrum during decay. The decay rate is however reduced for finite
$\unicode[STIX]{x1D70F}$ does not qualitatively change the shape of the spectrum during decay. The decay rate is however reduced for finite  $\unicode[STIX]{x1D70F}$. We also present results from high resolution (
$\unicode[STIX]{x1D70F}$. We also present results from high resolution (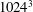 $1024^{3}$) direct numerical simulations of passive scalar mixing and decay. We find reasonable agreement with predictions of the Batchelor spectrum during steady state. The scalar spectrum during decay is however dependent on initial conditions. It agrees qualitatively with analytic predictions when power is dominantly in wavenumbers corresponding to the Batchelor regime, but is shallower when box-scale fluctuations dominate during decay.
$1024^{3}$) direct numerical simulations of passive scalar mixing and decay. We find reasonable agreement with predictions of the Batchelor spectrum during steady state. The scalar spectrum during decay is however dependent on initial conditions. It agrees qualitatively with analytic predictions when power is dominantly in wavenumbers corresponding to the Batchelor regime, but is shallower when box-scale fluctuations dominate during decay.