Published online by Cambridge University Press: 16 June 2016
The dynamics and pair trajectories of two self-propelled (active) colloids in a quiescent fluid for both axisymmetric and asymmetric cases are reported. The autonomous motions of the colloids are due to a catalytic chemical reaction taking place asymmetrically on their surfaces that generates a concentration gradient of interactive solutes around the particles and actuates particle propulsion. A combined analytical–numerical technique was developed to solve the coupled mass conservation equation for the solute and the hydrodynamics between the colloids in the Stokes flow regime. For axisymmetric motions, the translational swimming velocities of the particles in the near field can be enhanced or weakened (compared to their motions when they are far apart) depending on the relative orientations of their active sections. Moreover, it can be shown that different surface activities of two symmetric particles, e.g. an inert versus a catalytic particle or two catalytic particles, can also lead to a propulsion where the far-field swimming velocity for the inert and the catalytic particle attenuate as 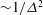 ${\sim}1/{\it\Delta}^{2}$ and
${\sim}1/{\it\Delta}^{2}$ and 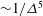 ${\sim}1/{\it\Delta}^{5}$ respectively,
${\sim}1/{\it\Delta}^{5}$ respectively, 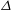 ${\it\Delta}$ is the non-dimensional centre-to-centre distance. For asymmetric motions, our analysis indicates two possible scenarios for pair trajectories of catalytically active particles: either the particles approach, come into contact and assemble or they interact and move away from each other (escape). It is found that the direction of particle rotations is the key factor in determining the escape or assembly scenario due to an interplay between both hydrodynamic and phoretic effects. Based on the analysis, a phase diagram is sketched for the pair trajectory of the catalytically active particles as a function of reacting surface coverages and their initial relative orientations with respect to each other. We believe this study has important implications in elucidation of collective behaviours of autophoretically self-propelled colloids and would be certainly a guide for experimentalists to design and control active systems.
${\it\Delta}$ is the non-dimensional centre-to-centre distance. For asymmetric motions, our analysis indicates two possible scenarios for pair trajectories of catalytically active particles: either the particles approach, come into contact and assemble or they interact and move away from each other (escape). It is found that the direction of particle rotations is the key factor in determining the escape or assembly scenario due to an interplay between both hydrodynamic and phoretic effects. Based on the analysis, a phase diagram is sketched for the pair trajectory of the catalytically active particles as a function of reacting surface coverages and their initial relative orientations with respect to each other. We believe this study has important implications in elucidation of collective behaviours of autophoretically self-propelled colloids and would be certainly a guide for experimentalists to design and control active systems.