Published online by Cambridge University Press: 27 November 2014
The lowest drag shape of fixed volume in Stokes flow has been known for some 40 years. It is front–back symmetric and similar to an American football with ends tangent to a cone of 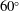 $60^{\circ }$. The analogous convex axisymmetric shape of fixed surface area, which may be of interest for particle design in chemistry and colloidal science, is characterised in this paper. This ‘other’ optimal shape has a surface vorticity proportional to the mean surface curvature, which is used with a local analysis of the flow near the tip to show that the front and rear ends are tangent to a cone of angle
$60^{\circ }$. The analogous convex axisymmetric shape of fixed surface area, which may be of interest for particle design in chemistry and colloidal science, is characterised in this paper. This ‘other’ optimal shape has a surface vorticity proportional to the mean surface curvature, which is used with a local analysis of the flow near the tip to show that the front and rear ends are tangent to a cone of angle 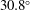 $30.8^{\circ }$. Using the boundary element method, we numerically represent the shape by expanding its tangent angle in terms decaying odd Legendre modes, and show that it has 11.3 % lower drag than a sphere of equal surface area, significantly more pronounced than for the fixed-volume optimal.
$30.8^{\circ }$. Using the boundary element method, we numerically represent the shape by expanding its tangent angle in terms decaying odd Legendre modes, and show that it has 11.3 % lower drag than a sphere of equal surface area, significantly more pronounced than for the fixed-volume optimal.