Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T11:23:12.207Z Has data issue: false hasContentIssue false
  • English
  • Français

The onset of turbulent rotating dynamos at the low magnetic Prandtl number limit

Published online by Cambridge University Press:  02 June 2017

Kannabiran Seshasayanan Open the ORCID record for Kannabiran Seshasayanan [Opens in a new window] ,
Vassilios Dallas Open the ORCID record for Vassilios Dallas [Opens in a new window]  and
Alexandros Alexakis Open the ORCID record for Alexandros Alexakis [Opens in a new window]
Kannabiran Seshasayanan
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, CNRS, Université Pierre et Marie Curie, Université Paris Diderot, Paris 75005, France
Vassilios Dallas
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, CNRS, Université Pierre et Marie Curie, Université Paris Diderot, Paris 75005, France Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
Alexandros Alexakis*
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, CNRS, Université Pierre et Marie Curie, Université Paris Diderot, Paris 75005, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We demonstrate that the critical magnetic Reynolds number 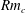$Rm_{c}$ for a turbulent non-helical dynamo in the limit of low magnetic Prandtl number 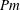$Pm$ (i.e. 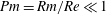$Pm=Rm/Re\ll 1$ ) can be significantly reduced if the flow is subjected to global rotation. Even for moderate rotation rates the required energy injection rate can be reduced by a factor of more than 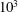$10^{3}$ . This strong decrease in the onset is attributed to the transfer of energy to the large scales, forming a large-scale condensate, and the reduction in the turbulent fluctuations that cause the flow to have a much larger cutoff length scale than in a non-rotating flow of the same Reynolds number. The dynamo thus behaves as if it is driven just by the large scales that act as a laminar flow (i.e. it behaves as a high 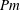$Pm$ dynamo) even though the actual Reynolds number is much higher than the magnetic Reynolds number (i.e. low 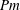$Pm$ ). Our finding thus points to a new paradigm for the design of new experiments on liquid metal dynamos.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Geodynamo Turbulent Flows: Rotating turbulence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , R3
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2015 Rotating Taylor–Green flow. J. Fluid Mech. 769, 46–78.Google Scholar
Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.Google Scholar
Cameron, A. & Alexakis, A. 2016 Fate of alpha dynamos at large Rm . Phys. Rev. Lett. 117, 205101.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2014 Direct and inverse energy cascades in a forced rotating turbulence experiment. Phys. Fluids 26 (12), 125112.CrossRefGoogle Scholar
Campagne, A., Machicoane, N., Gallet, B., Cortet, P. & Moisy, F. 2016 Turbulent drag in a rotating frame. J. Fluid Mech. 794, R5.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166 (1), 97–114.Google Scholar
Dallas, V. & Tobias, S. M. 2016 Forcing-dependent dynamics and emergence of helicity in rotating turbulence. J. Fluid Mech. 798, 682–695.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Gailitis, A., Lielausis, O., Platacis, E., Dement’ev, S., Cifersons, A., Gerbeth, G., Gundrum, T., Stefani, F., Christen, M. & Will, G. 2001 Magnetic field saturation in the Riga dynamo experiment. Phys. Rev. Lett. 86, 3024–3027.CrossRefGoogle ScholarPubMed
Gallet, B. 2015 Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows. J. Fluid Mech. 783, 412–447.CrossRefGoogle Scholar
Giesecke, A., Stefani, F., Gundrum, T., Gerbeth, G., Nore, C. & Lorat, J. 2012 Experimental realization of dynamo action: present status and prospects. In Solar and Astrophysical Dynamos and Magnetic Activity, Proc. IAU, vol. 8, pp. 411–416. Cambridge University Press.Google Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2014 Large-scale vortices in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 758, 407–435.Google Scholar
Iskakov, A. B., Schekochihin, A. A., Cowley, S. C., McWilliams, J. C. & Proctor, M. R. E. 2007 Numerical demonstration of fluctuation dynamo at low magnetic Prandtl numbers. Phys. Rev. Lett. 98, 208501.CrossRefGoogle ScholarPubMed
Kunnen, R. P. J., Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R. & Lohse, D. 2016 Transition to geostrophic convection: the role of the boundary conditions. J. Fluid Mech. 799, 413–432.Google Scholar
Mininni, P. D. & Montgomery, D. C. 2005 Low magnetic Prandtl number dynamos with helical forcing. Phys. Rev. E 72, 056320.Google Scholar
Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI–OpenMp scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37 (6), 316–326.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Monchaux, R., Berhanu, M., Bourgoin, M., Moulin, M., Odier, P., Pinton, J.-F., Volk, R., Fauve, S., Mordant, N., Pétrélis, F. et al. 2007 Generation of a magnetic field by dynamo action in a turbulent flow of liquid sodium. Phys. Rev. Lett. 98, 044502.Google Scholar
Morin, J., Donati, J.-F., Petit, P., Delfosse, X., Forveille, T. & Jardine, M. M. 2010 Large-scale magnetic topologies of late M dwarfs. Mon. Not. R. Astron. Soc. 407, 2269–2286.Google Scholar
Nornberg, M. D., Spence, E. J., Kendrick, R. D., Jacobson, C. M. & Forest, C. B. 2006 Intermittent magnetic field excitation by a turbulent flow of liquid sodium. Phys. Rev. Lett. 97, 044503.CrossRefGoogle ScholarPubMed
Pétrélis, F., Mordant, N. & Fauve, S. 2007 On the magnetic fields generated by experimental dynamos. Geophys. Astrophys. Fluid Dyn. 101 (3–4), 289–323.Google Scholar
Plumley, M., Julien, K., Marti, P. & Stellmach, S. 2016 The effects of Ekman pumping on quasi-geostrophic Rayleigh–Bénard convection. J. Fluid Mech. 803, 51–71.Google Scholar
Ponty, Y., Mininni, P. D., Montgomery, D. C., Pinton, J.-F., Politano, H. & Pouquet, A. 2005 Numerical study of dynamo action at low magnetic Prandtl numbers. Phys. Rev. Lett. 94, 164502.Google Scholar
Ponty, Y. & Plunian, F. 2011 Transition from large-scale to small-scale dynamo. Phys. Rev. Lett. 106, 154502.CrossRefGoogle ScholarPubMed
Proctor, M. R. E. & Gilbert, A. D. 1994 Lectures on Solar and Planetary Dynamos. Cambridge University Press.CrossRefGoogle Scholar
Reiners, A., Basri, G. & Browning, M. 2009 Evidence for magnetic flux saturation in rapidly rotating M stars. Astrophys. J. 692 (1), 538–545.Google Scholar
Sadek, M., Alexakis, A. & Fauve, S. 2016 Optimal length scale for a turbulent dynamo. Phys. Rev. Lett. 116, 074501.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016a Kazantsev model in non-helical 2.5-dimensional flows. J. Fluid Mech. 806, 627–648.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016b Turbulent 2.5-dimensional dynamos. J. Fluid Mech. 799, 246–264.CrossRefGoogle Scholar
Shew, W. L. & Lathrop, D. P. 2005 Liquid sodium model of geophysical core convection. Phys. Earth Planet. Inter. 153, 136–149.Google Scholar
Smith, S. G. L. & Tobias, S. M. 2004 Vortex dynamos. J. Fluid Mech. 498, 1–21.Google Scholar
Stieglitz, R. & Mueller, U. 2001 Experimental demonstration of a homogeneous two-scale dynamo. Phys. Fluids 13 (3), 561–564.Google Scholar
Tobias, S. M. & Cattaneo, F. 2008a Dynamo action in complex flows: the quick and the fast. J. Fluid Mech. 601, 101–122.CrossRefGoogle Scholar
Tobias, S. M. & Cattaneo, F. 2008b Limited role of spectra in dynamo theory: coherent versus random dynamos. Phys. Rev. Lett. 101 (12), 125003.Google Scholar
Tobias, S. M., Cattaneo, F. & Boldyrev, S. 2011 MHD dynamos and turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), pp. 351–397. Cambridge University Press.Google Scholar
Yarom, E., Vardi, Y. & Sharon, E. 2013 Experimental quantification of inverse energy cascade in deep rotating turbulence. Phys. Fluids 25 (8), 085105.Google Scholar