Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T09:16:59.215Z Has data issue: false hasContentIssue false
  • English
  • Français

On the couple dynamics of wall-mounted flexible plates in tandem

Published online by Cambridge University Press:  03 August 2018

Y. Jin ,
J.-T. Kim ,
Z. Mao  and
L. P. Chamorro Open the ORCID record for L. P. Chamorro [Opens in a new window]
Y. Jin
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
J.-T. Kim
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Z. Mao
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA State Key Laboratory of Hydroscience and Engineering and Department of Energy and Power Engineering, Tsinghua University, Beijing, 100084, China
L. P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering, University of Illinois, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

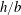The dynamics of two rectangular, flexible plates of low aspect ratio $h/b$ (height/width = 4) was experimentally investigated in tandem arrangements under uniform flows at various Cauchy numbers 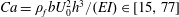$Ca=\unicode[STIX]{x1D70C}_{f}bU_{0}^{2}h^{3}/(EI)\in [15,77]$ (where 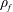$\unicode[STIX]{x1D70C}_{f}$ is the fluid density, 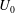$U_{0}$ is the incoming flow velocity, 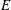$E$ is the Young’s modulus and 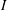$I$ is the second moment of the area) and spacings 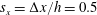$s_{x}=\unicode[STIX]{x0394}x/h=0.5$, 1 and 2. Planar particle image velocimetry (PIV) and particle tracking velocimetry (PTV) were used to characterize the surrounding flow field and oscillations of the wall-mounted structures. Results show that the oscillations of the upstream plate were dominated by its natural frequency. However, the motions of the downstream plate were significantly modulated by the induced flow and coherent motions shed from the upstream structure. Such modulation led to highly correlated motions between the plates with similar amplitude in the case 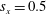$s_{x}=0.5$, to comparatively larger oscillation amplitude of the downstream plate in the intermediate separation 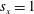$s_{x}=1$, and roughly decoupled interaction for 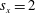$s_{x}=2$. Despite that the intensity of the oscillations of the upstream plate increased monotonically with 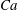$Ca$, this was not the case for the downstream plate at 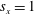$s_{x}=1$ and 2 due to flow fluctuations, vortex shedding and large structure deformation; as a result, it exhibited a local minimum. Supported with measurements, a mathematical model was derived to quantitatively explain this behaviour.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , R2
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420 (6915), 479–481.Google Scholar
Alben, S., Shelley, M. & Zhang, J. 2004 How flexibility induces streamlining in a two-dimensional flow. Phys. Fluids 16 (5), 1694–1713.Google Scholar
Bai, K. & Katz, J. 2014 On the refractive index of sodium iodide solutions for index matching in PIV. Exp. Fluids 55, 1–6.Google Scholar
Barsu, S., Doppler, D., Jerome, J. J. S., Rivière, N. & Lance, M. 2016 Drag measurements in laterally confined 2D canopies: reconfiguration and sheltering effect. Phys. Fluids 28 (10), 107101.Google Scholar
Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity–wake interference region. J. Fluid Mech. 621, 321–364.Google Scholar
Brunet, Y., Finnigan, J. J. & Raupach, M. R. 1994 A wind tunnel study of air flow in waving wheat: single-point velocity statistics. Boundary-Layer Meteorol. 70 (1–2), 95–132.Google Scholar
Chen, L. 2010 An integral approach for large deflection cantilever beams. Intl J. Non-Linear Mech. 45 (3), 301–305.Google Scholar
Gopalkrishnan, R.1993 Vortex-induced forces on oscillating bluff cylinders (No. WHOI-92-38). Woods Hole Oveanographic Institution MA.Google Scholar
Gosselin, F., De Langre, E. & Machado-Almeida, B. A. 2010 Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 650, 319–341.Google Scholar
Huang, H., Wei, H. & Lu, X.-Y. 2018 Coupling performance of tandem flexible inverted flags in a uniform flow. J. Fluid Mech. 837, 461–476.Google Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2011 Vortex and wake-induced vibrations of a tandem arrangement of two flexible circular cylinders with near wake interference. J. Fluids Struct. 27 (2), 193–211.Google Scholar
Huera-Huarte, F. J. & Gharib, M. 2011 Vortex-and wake-induced vibrations of a tandem arrangement of two flexible circular cylinders with far wake interference. J. Fluids Struct. 27 (5–6), 824–828.Google Scholar
Jin, Y. & Chamorro, L. P. 2017 On the dynamics of three-dimensional slung prisms under very low and high turbulence flows. J. Fluid Mech. 816, 468–480.Google Scholar
Jin, Y., Ji, S. & Chamorro, L. P. 2016 Spectral energy cascade of body rotations and oscillations under turbulence. Phys. Rev. E 94 (6), 063105.Google Scholar
Jin, Y., Kim, J.-T. & Chamorro, L. P. 2018 Instability-driven frequency decoupling between structure dynamics and wake fluctuations. Phys. Rev. Fluids 3 (4), 044701.Google Scholar
Khabbouchi, I., Fellouah, H., Ferchichi, M. & Guellouz, M. S. 2014 Effects of free-stream turbulence and Reynolds number on the separated shear layer from a circular cylinder. J. Wind Engng Ind. Aerodyn. 135, 46–56.Google Scholar
Kim, J.-T., Kim, D., Liberzon, A. & Chamorro, L. P. 2016 Three-dimensional particle tracking velocimetry for turbulence applications: case of a jet flow. J. Vis. Exp. 108, e53745.Google Scholar
Kim, S., Huang, W.-X. & Sung, H. J. 2010 Constructive and destructive interaction modes between two tandem flexible flags in viscous flow. J. Fluid Mech. 661, 511–521.Google Scholar
Knisely, C. W. 1990 Strouhal numbers of rectangular cylinders at incidence: a review and new data. J. Fluids Struct. 4 (4), 371–393.Google Scholar
Leclercq, T. & de Langre, E. 2018 Reconfiguration of elastic blades in oscillatory flow. J. Fluid Mech. 838, 606–630.Google Scholar
Leclercq, T., Peake, N. & de Langre, E. 2018 Does flutter prevent drag reduction by reconfiguration? Proc. R. Soc. Lond. A 474 (2209), 20170678.Google Scholar
Lin, C. & Glendening, W. 2002 Large eddy simulation of an inhomogeneous atmospheric boundary layer under neutral conditions. J. Atmos. Sci. 59, 2479–2497.Google Scholar
Lin, J.-C., Yang, Y. & Rockwell, D. 2002 Flow past two cylinders in tandem: instantaneous and averaged flow structure. J. Fluids Struct. 16 (8), 1059–1071.Google Scholar
Liu, B., Hamed, A. M. & Chamorro, L. P. 2018 On the Kelvin–Helmholtz and von Kármán vortices in the near-wake of semicircular cylinders with flaps. J. Turbul. 19 (1), 61–71.Google Scholar
Luhar, M. & Nepf, H. M. 2011 Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 56 (6), 2003–2017.Google Scholar
Luhar, M. & Nepf, H. M. 2016 Wave-induced dynamics of flexible blades. J. Fluids Struct. 61, 20–41.Google Scholar
Mullarney, J. C. & Henderson, S. M. 2010 Wave-forced motion of submerged single-stem vegetation. J. Geophys. Res.-Oceans 115, C12061.Google Scholar
Norberg, C. 1993 Flow around rectangular cylinders: pressure forces and wake frequencies. J. Wind Engng Ind. Aerodyn. 49 (1), 187–196.Google Scholar
Novak, M. D., Warland, J. S., Orchansky, A. L., Ketler, R. & Green, S. 2000 Wind tunnel and field measurements of turbulent flow in forests. Part I: uniformly thinned stands. Boundary-Layer Meteorol. 95 (3), 457–495.Google Scholar
Ristroph, L. & Zhang, J. 2008 Anomalous hydrodynamic drafting of interacting flapping flags. Phys. Rev. Lett. 101 (19), 194502.Google Scholar
Thom, A. S. 1971 Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 97 (414), 414–428.Google Scholar
Wang, E., Xiao, Q., Zhu, Q. & Incecik, A. 2017 The effect of spacing on the vortex-induced vibrations of two tandem flexible cylinders. Phys. Fluids 29 (7), 077103.Google Scholar
Younis, M. Y., Alam, M. M. & Zhou, Y. 2016 Flow around two non-parallel tandem cylinders. Phys. Fluids 28 (12), 125106.Google Scholar
Zhao, M. 2015 Flow-induced vibrations of square and rectangular cylinders at low Reynolds number. Fluid Dyn. Res. 47 (2), 025502.Google Scholar