Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-09T09:04:14.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear reflection of a two-dimensional finite-width internal gravity wave on a slope

Published online by Cambridge University Press:  30 January 2020

Matthieu Leclair Open the ORCID record for Matthieu Leclair [Opens in a new window] ,
Keshav Raja Open the ORCID record for Keshav Raja [Opens in a new window]  and
Chantal Staquet Open the ORCID record for Chantal Staquet [Opens in a new window]
Matthieu Leclair*
Affiliation:
Univ. Grenoble Alpes, CNRS, Grenoble INP, LEGI, 38000Grenoble, France
Keshav Raja*
Affiliation:
Univ. Grenoble Alpes, CNRS, Grenoble INP, LEGI, 38000Grenoble, France
Chantal Staquet*
Affiliation:
Univ. Grenoble Alpes, CNRS, Grenoble INP, LEGI, 38000Grenoble, France
*
‡Present address: ETH Zürich, Universitätstrasse 16, 8092 Zürich, Switzerland
§Present address: The University of Southern Mississippi, Marine Science, 1020 Balch Blvd Stennis Space Center, MS 39529, USA
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

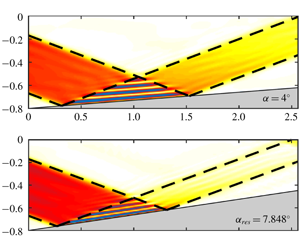
The nonlinear reflection of a finite-width plane internal gravity wave incident onto a uniform slope is addressed, relying on the inviscid theory of Thorpe (J. Fluid Mech., vol. 178, 1987, pp. 279–302) for pure plane waves. The aim of this theory is to determine the conditions under which the incident and the reflected waves form a resonant triad with the second-harmonic wave resulting from their interaction. Thorpe’s theory leads to an indeterminacy of the second-harmonic wave amplitude at resonance. In waiving this indeterminacy, we show that the latter amplitude has a finite behaviour at resonance, increasing linearly from the slope. We investigate the influence of background rotation and find similar results with a weaker growth rate. We then adapt the theory to the case of an incident plane wave of finite width. In this case, nonlinear interactions are confined to the area where the incident and reflected finite-width waves superpose, implying that the amplitude of the second-harmonic wave is bounded at resonance. We find good agreement with the results of numerical simulations in a vertical plane as long as the dissipated power of the incident and reflected waves remain smaller than the power transferred to the second-harmonic wave. This is the case for small slope angles. As the slope angle increases, the focusing of the reflected wave enhances viscous effects and dissipation eventually dominates over nonlinear transfer. We finally discuss the relevance of laboratory experiments to assess the validity of the theoretical results.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 887 , 25 March 2020 , A31
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aiki, H. & Yamagata, T. 2004 A numerical study on the successive formation of Meddy like lenses. J. Geophys. Res. 109, C06020.CrossRefGoogle Scholar
Bordes, G., Venaille, A., Joubaud, S. & Odier, P. 2012 Experimental observation of a strong mean flow induced by internal gravity waves. Phys. Fluids 24, 086602.CrossRefGoogle Scholar
Chalamalla, V. K., Vamsi, K., Gayen, B., Scotti, A. & Sarkar, S. 2013 Turbulence during the reflection of internal gravity waves at critical and near-critical slopes. J. Fluid Mech. 729, 47–68.CrossRefGoogle Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Academic.Google Scholar
Gostiaux, L., Dauxois, T., Didelle, H., Sommeria, J. & Viboux, S. 2006 Quantitative laboratory observations of internal wave reflection on ascending slopes. Phys. Fluids 18, 056602.CrossRefGoogle Scholar
Gostiaux, L., Didelle, H., Mercier, S. & Dauxois, T. 2007 A novel internal waves generator. Exp. Fluids 42, 123–130.CrossRefGoogle Scholar
Grisouard, N., Leclair, M., Gostiaux, L. & Staquet, C. 2013 Large scale energy transfer from an internal gravity wave reflecting on a simple slope. Proc. IUTAM 8, 119–128.CrossRefGoogle Scholar
Hosegood, P. & van Haren, H. 2004 Near-bed solibores over the continental slope in the Faroe-Shetland channel. Deep-Sea Res. II 51, 2943–2971.CrossRefGoogle Scholar
Kataoka, T. & Akylas, T. 2015 On three-dimensional internal gravity wave beams and induced large-scale mean flows. J. Fluid Mech. 769, 621–634.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1969 On the transport of mass by time-varying ocean currents. Deep Sea Res. 16 (5), 431–447.Google Scholar
McPhee-Shaw, E. E. & Kunze, E. 2002 Boundary layer intrusions from a sloping bottom: a mechanism for generating intermediate nepheloid layers. J. Geophys. Res. 107 (C6), 3050.CrossRefGoogle Scholar
Pairaud, I., Staquet, C., Sommeria, J. & Mahdizadeh, M. M. 2010 Generation of harmonics and sub-harmonics from an internal tide in a uniformly stratified fluid: numerical and laboratory experiments. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans: IUTAM Bookseries, vol. 28, pp. 52–63. Springer.CrossRefGoogle Scholar
Phillips, O. M. 1966 Dynamics of The Upper Ocean. Cambridge University Press.Google Scholar
Rodenborn, B., Kiefer, D., Zhang, H. P. & Swinney, H. L. 2011 Harmonic generation by reflecting internal waves. Phys. Fluids 23, 026601.CrossRefGoogle Scholar
Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.CrossRefGoogle Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. G. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.CrossRefGoogle Scholar
Thorpe, S. A. 1968 On the shape of progressive internal waves. Phil. Trans. R. Soc. Lond. A 263 (1145), 563–614.Google Scholar
Thorpe, S. A. 1987 On the reflection of a train of finite-amplitude internal waves from a uniform slope. J. Fluid Mech. 178, 279–302.CrossRefGoogle Scholar
Thorpe, S. A. 1997 On the interactions of internal waves reflecting from slopes. J. Phys. Oceanogr. 27, 2072–2078.2.0.CO;2>CrossRefGoogle Scholar
Thorpe, S. A. 2001 On the reflection of internal wave groups from sloping topography. J. Phys. Oceanogr. 31, 3121–3126.2.0.CO;2>CrossRefGoogle Scholar
Wunsch, C. 1971 Note on some Reynolds stress effects of internal waves on slopes. Deep-Sea Res. 18 (6), 583–591.Google Scholar