Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T12:20:46.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear optimal control of transition due to a pair of vortical perturbations using a receding horizon approach

Published online by Cambridge University Press:  27 December 2018

Dandan Xiao  and
George Papadakis Open the ORCID record for George Papadakis [Opens in a new window]
Dandan Xiao
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
George Papadakis*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers the nonlinear optimal control of transition in a boundary layer flow subjected to a pair of free stream vortical perturbations using a receding horizon approach. The optimal control problem is solved using the Lagrange variational technique that results in a set of linearized adjoint equations, which are used to obtain the optimal wall actuation (blowing and suction from a control slot located in the transition region). The receding horizon approach enables the application of control action over a longer time period, and this allows the extraction of time-averaged statistics as well as investigation of the control effect downstream of the control slot. The results show that the controlled flow energy is initially reduced in the streamwise direction and then increased because transition still occurs. The distribution of the optimal control velocity responds to the flow activity above and upstream of the control slot. The control effect propagates downstream of the slot and the flow energy is reduced up to the exit of the computational domain. The mean drag reduction is 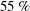$55\,\%$ and 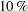$10\,\%$ in the control region and downstream of the slot, respectively. The control mechanism is investigated by examining the second-order statistics and the two-point correlations. It is found that in the upstream (left) side of the slot, the controller counteracts the near-wall high-speed streaks and reduces the turbulent shear stress; this is akin to opposition control in channel flow, and because the time-average control velocity is positive, it is more similar to blowing-only opposition control. In the downstream (right) side of the slot, the controller reacts to the impingement of turbulent spots that have been produced upstream and inside the boundary layer (top–bottom mechanism). The control velocity is positive and increases in the streamwise direction, and the flow behaviour is similar to that of uniform blowing.

JFM classification

Boundary Layers: Boundary layer control Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 524 - 555
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbassi, M. R., Baars, W. J., Hutchins, N. & Marusic, I. 2017 Skin-friction drag reduction in a high-Reynolds-number turbulent boundary layer via real-time control of large-scale structures. Intl J. Heat Fluid Flow 67, 30–41.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009 Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Bewley, T. R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithms. J. Fluid Mech. 447, 179–225.Google Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.Google Scholar
Chang, Y., Collis, S. S. & Ramakrishnan, S. 2002 Viscous effects in control of near-wall turbulence. Phys. Fluids 14 (11), 4069–4080.Google Scholar
Cherubini, S., Robinet, J.-C. & De Palma, P. 2013 Nonlinear control of unsteady finite-amplitude perturbations in the Blasius boundary-layer flow. J. Fluid Mech. 737, 440–465.Google Scholar
Chevalier, M., Hœpffner, J., Åkervik, E. & Henningson, D. S. 2007 Linear feedback control and estimation applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 588, 163–187.Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Chung, Y. M. & Talha, T. 2011 Effectiveness of active flow control for turbulent skin friction drag reduction. Phys. Fluids 23 (2), 025102.Google Scholar
Flinois, T. L. B. & Colonius, T. 2015 Optimal control of circular cylinder wakes using long control horizons. Phys. Fluids 27 (8), 087105.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Hack, M. J. P. & Zaki, T. A. 2014 The influence of harmonic wall motion on transitional boundary layers. J. Fluid Mech. 760, 63–94.Google Scholar
Hodson, H. P. & Howell, R. J. 2005 Bladerow interactions, transition, and high-lift aerofoils in low-pressure turbines. Annu. Rev. Fluid Mech. 37, 71–98.Google Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.Google Scholar
Kametani, Y. & Fukagata, K. 2011 Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction. J. Fluid Mech. 681, 154–172.Google Scholar
Kametani, Y., Fukagata, K., Örlü, R. & Schlatter, P. 2015 Effect of uniform blowing/suction in a turbulent boundary layer at moderate Reynolds number. Intl J. Heat Fluid Flow 55, 132–142.Google Scholar
Kim, K. & Sung, H. J. 2006 Effects of unsteady blowing through a spanwise slot on a turbulent boundary layer. J. Fluid Mech. 557, 423–450.Google Scholar
Lardeau, S. & Leschziner, M. A. 2013 The streamwise drag-reduction response of a boundary layer subjected to a sudden imposition of transverse oscillatory wall motion. Phys. Fluids 25 (7), 075109.Google Scholar
Lee, C., Kim, J., Babcock, D. & Goodman, R. 1997 Application of neural networks to turbulence control for drag reduction. Phys. Fluids 9 (6), 1740–1747.Google Scholar
Mao, X., Blackburn, H. M. & Sherwin, S. J. 2015 Nonlinear optimal suppression of vortex shedding from a circular cylinder. J. Fluid Mech. 775, 241–265.Google Scholar
Monokrousos, A., Brandt, L., Schlatter, P. & Henningson, D. S. 2008 DNS and LES of estimation and control of transition in boundary layers subject to free-stream turbulence. Intl J. Heat Fluid Flow 29 (3), 841–855.Google Scholar
Naguib, A. M., Morrison, J. F. & Zaki, T. A. 2010 On the relationship between the wall-shear-stress and transient-growth disturbances in a laminar boundary layer. Phys. Fluids 22 (5), 054103.Google Scholar
Nakanishi, R., Mamori, H. & Fukagata, K. 2012 Relaminarization of turbulent channel flow using traveling wave-like wall deformation. Intl J. Heat Fluid Flow 35, 152–159.Google Scholar
Nolan, K. P. & Zaki, T. A. 2013 Conditional sampling of transitional boundary layers in pressure gradients. J. Fluid Mech. 728, 306–339.Google Scholar
Pamiès, M., Garnier, E., Merlen, A. & Sagaut, P. 2007 Response of a spatially developing turbulent boundary layer to active control strategies in the framework of opposition control. Phys. Fluids 19 (10), 108102.Google Scholar
Papadakis, G., Lu, L. & Ricco, P. 2016 Closed-loop control of boundary layer streaks induced by free-stream turbulence. Phys. Rev. Fluids 1 (4), 043501.Google Scholar
Park, J. & Choi, H. 1999 Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow. Phys. Fluids 11 (10), 3095–3105.Google Scholar
Passaggia, P. & Ehrenstein, U. 2013 Adjoint based optimization and control of a separated boundary-layer flow. Eur. J. Mech. (B/Fluids) 41, 169–177.Google Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.Google Scholar
Schlatter, P. & Orlu, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Stroh, A., Frohnapfel, B., Schlatter, P. & Hasegawa, Y. 2015 A comparison of opposition control in turbulent boundary layer and turbulent channel flow. Phys. Fluids 27 (7), 075101.Google Scholar
Stroh, A., Hasegawa, Y., Schlatter, P. & Frohnapfel, B. 2016 Global effect of local skin friction drag reduction in spatially developing turbulent boundary layer. J. Fluid Mech. 805, 303–321.Google Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33 (7), 1220–1228.Google Scholar
Tomiyama, N. & Fukagata, K. 2013 Direct numerical simulation of drag reduction in a turbulent channel flow using spanwise traveling wave-like wall deformation. Phys. Fluids 25 (10), 105115.Google Scholar
Vaughan, N. J. & Zaki, T. A. 2011 Stability of zero-pressure-gradient boundary layer distorted by unsteady Klebanoff streaks. J. Fluid Mech. 681, 116–153.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.Google Scholar
Wang, Q. 2013 Forward and adjoint sensitivity computation of chaotic dynamical systems. J. Comput. Phys. 235, 1–13.Google Scholar
Wissink, J. G., Zaki, T. A., Rodi, W. & Durbin, P. A. 2014 The effect of wake turbulence intensity on transition in a compressor cascade. Flow Turbul. Combust. 93 (4), 555–576.Google Scholar
Xiao, D. & Papadakis, G 2017 Nonlinear optimal control of bypass transition in a boundary layer flow. Phys. Fluids 29 (5), 054103.Google Scholar
Yudhistira, I. & Skote, M. 2011 Direct numerical simulation of a turbulent boundary layer over an oscillating wall. J. Turbul. 12, N9.Google Scholar
Zaki, T. A. & Durbin, P. A. 2005 Mode interaction and the bypass route to transition. J. Fluid Mech. 531, 85–111.Google Scholar
Zaki, T. A., Wissink, J. G., Rodi, W. & Durbin, P. A. 2010 Direct numerical simulations of transition in a compressor cascade: the influence of free-stream turbulence. J. Fluid Mech. 665, 57–98.Google Scholar