Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T14:40:46.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-canonical Hamiltonian structure and Poisson bracket for two-dimensional hydrodynamics with free surface

Published online by Cambridge University Press:  30 April 2019

A. I. Dyachenko Open the ORCID record for A. I. Dyachenko [Opens in a new window] ,
P. M. Lushnikov Open the ORCID record for P. M. Lushnikov [Opens in a new window]  and
V. E. Zakharov
A. I. Dyachenko
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Moscow, Russia
P. M. Lushnikov*
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Moscow, Russia Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, USA
V. E. Zakharov
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Moscow, Russia Department of Mathematics, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Euler equations for the potential flow of an ideal incompressible fluid of infinite depth with a free surface in two-dimensional geometry. Both gravity and surface tension forces are taken into account. A time-dependent conformal mapping is used which maps the lower complex half-plane of the auxiliary complex variable 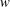$w$ into the fluid’s area, with the real line of 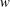$w$ mapped into the free fluid’s surface. We reformulate the exact Eulerian dynamics through a non-canonical non-local Hamiltonian structure for a pair of the Hamiltonian variables. These two variables are the imaginary part of the conformal map and the fluid’s velocity potential, both evaluated at the fluid’s free surface. The corresponding Poisson bracket is non-degenerate, i.e. it does not have any Casimir invariant. Any two functionals of the conformal mapping commute with respect to the Poisson bracket. The new Hamiltonian structure is a generalization of the canonical Hamiltonian structure of Zakharov (J. Appl. Mech. Tech. Phys., vol. 9(2), 1968, pp. 190–194) which is valid only for solutions for which the natural surface parametrization is single-valued, i.e. each value of the horizontal coordinate corresponds only to a single point on the free surface. In contrast, the new non-canonical Hamiltonian equations are valid for arbitrary nonlinear solutions (including multiple-valued natural surface parametrization) and are equivalent to the Euler equations. We also consider a generalized hydrodynamics with the additional physical terms in the Hamiltonian beyond the Euler equations. In that case we identify powerful reductions that allow one to find general classes of particular solutions.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Hamiltonian theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 526 - 552
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I. 1989 Mathematical Methods of Classical Mechanics. Springer.Google Scholar
Bensimon, D., Kadanoff, L. P., Liang, S., Shraiman, B. I. & Tang, C. 1986 Viscous flows in two dimensions. Rev. Mod. Phys. 58, 977–999.Google Scholar
Chalikov, D. & Sheinin, D. 1998 Direct modeling of one-dimensional nonlinear potential waves. Adv. Fluid Mech. 17, 207–258.Google Scholar
Chalikov, D. & Sheinin, D. 2005 Modeling of extreme waves based on equation of potential flow with a free surface. J. Comput. Phys. 210, 247–273.Google Scholar
Chalikov, D. V. 2016 Numerical Modeling of Sea Waves. Springer.Google Scholar
Cole, M. W. & Cohen, M. H. 1969 Image-potential-induced surface bands in insulators. Phys. Rev. Lett. 23, 1238.Google Scholar
Craig, W. & Sulem, C. 1993 Numerical simulation of gravity waves. J. Comput. Phys. 108, 73–83.Google Scholar
Crapper, G. D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2, 532–540.Google Scholar
Crowdy, D. G. 1999 Circulation-induced shape deformations of drops and bubbles: exact two-dimensional models. Phys. Fluids 11, 2836–2845.10.1063/1.870142Google Scholar
Crowdy, D. G. 2000a A new approach to free surface Euler flows with capillarity. Stud. Appl. Maths 105, 35–58.Google Scholar
Crowdy, D. G. 2000b Hele-Shaw flows and water waves. J. Fluid Mech. 409, 223–242.Google Scholar
Dyachenko, A. I. 2001 On the dynamics of an ideal fluid with a free surface. Dokl. Math. 63 (1), 115–117.Google Scholar
Dyachenko, A. I., Kachulin, D. I. & Zakharov, V. E. 2013 On the nonintegrability of the free surface hydrodynamics. JETP Lett. 98, 43–47.Google Scholar
Dyachenko, A. I., Kuznetsov, E. A., Spector, M. & Zakharov, V. E. 1996 Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 221, 73–79.Google Scholar
Dyachenko, A. I. & Zakharov, V. E. 1994 Is free surface hydrodynamics an integrable system? Phys. Lett. A 190 (2), 144–148.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2016 Branch cuts of Stokes wave on deep water. Part I. Numerical solution and Padé approximation. Stud. Appl. Maths 137, 419–472.Google Scholar
Edelman, V. S. 1980 Levitated electrons. Sov. Phys. Usp. 23, 227–244.Google Scholar
Fefferman, C. 1971 Characterizations of bounded mean oscillation. Bull. Am. Math. Soc. 77, 587–588.Google Scholar
Fefferman, C. & Stein, E. M. 1972 H p spaces of several variables. Acta Math. 71, 137–193.Google Scholar
Flierl, G. R., Morrison, P. J. & Swaminathan, R. V.2018 Jovian vortices and jets.arXiv:1809.08671.Google Scholar
Gakhov, F. D. 1966 Boundary Value Problems. Pergamon.Google Scholar
Galin, L. A. 1945 Unsteady filtration with free surface. Dokl. Akad. Nauk SSSR 47, 246–249.Google Scholar
Gardner, C. S., Greene, J. M., Kruskal, M. D. & Miura, R. M. 1967 Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 19, 1095.Google Scholar
Grant, M. A. 1973 Standing Stokes waves of maximum height. J. Fluid Mech. 60 (3), 593–604.Google Scholar
Hilbert, D. 1905 Üeber eine Anwendung der Integralgleichungen auf ein Problem der Funktionentheorie. In Verhandlungen des dritten internationalen Mathematiker Kongresses in Heidelberg 1904 (ed. Krazer, A.), pp. 233–240. Teubner.Google Scholar
Howison, S. D. 1986 Cusp development in Hele-Shaw flow with a free surface. SIAM J. Appl. Maths 46, 20–26.10.1137/0146003Google Scholar
Kharif, C. & Pelinovsky, E. 2003 Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. (B/Fluids) 22, 603–634.10.1016/j.euromechflu.2003.09.002Google Scholar
Kuznetsov, E. A. & Lushnikov, P. M. 1995 Nonlinear theory of the excitation of waves by a wind due to the Kelvin–Helmholtz instability. J. Expl Theor. Phys. 81, 332–340.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1989 Fluid Mechanics, 3rd edn., vol. 6. Pergamon.Google Scholar
Lushnikov, P. M. & Zubarev, N. M. 2018 Exact solutions for nonlinear development of a Kelvin–Helmholtz instability for the counterflow of superfluid and normal components of helium II. Phys. Rev. Lett. 120, 204504.10.1103/PhysRevLett.120.204504Google Scholar
Lushnikov, P. M. 2016 Structure and location of branch point singularities for Stokes waves on deep water. J. Fluid Mech. 800, 557–594.Google Scholar
Lushnikov, P. M. & Zakharov, V. E. 2005 On optimal canonical variables in the theory of ideal fluid with free surface. Physica D 203, 9–29.Google Scholar
Meison, D., Orzag, S. & Izraely, M. 1981 Applications of numerical conformal mapping. J. Comput. Phys. 40, 345–360.Google Scholar
Mineev-Weinstein, M., Wiegmann, P. B. & Zabrodin, A. 2000 Integrable structure of interface dynamics. Phys. Rev. Lett. 84 (22), 5106–5109.Google Scholar
Mineev-Weinstein, M. B. & Dawson, S. P. 1994 Class of nonsingular exact solutions for Laplacian pattern formation. Phys. Rev. E 50, R24–R27.Google Scholar
Morrison, P. J. 1998 Hamiltonian description of the ideal fluid. Rev. Mod. Phys. 70, 467–521.Google Scholar
Morrison, P. J. 2005 Hamiltonian and action principle formulations of plasma physics. Phys. Plasmas 12, 058102.Google Scholar
Novikov, S., Manakov, S. V., Pitaevskii, L. P. & Zakharov, V. E. 1984 Theory of Solitons: The Inverse Scattering Method. Springer.Google Scholar
Ovsyannikov, L. V. 1973 Dynamics of a fluid. M.A. Lavrent’ev Institute of Hydrodynamics Sib. Branch USSR Ac. Sci. 15, 104–125.Google Scholar
Pandey, J. N. 1996 The Hilbert Transform of Schwartz Distributions and Applications. Wiley.Google Scholar
Penney, W. G. & Price, A. T. 1952 Part II. Finite periodic stationary gravity waves in a perfect liquid. Phil. Trans. R. Soc. Lond. A 244, 254–284.Google Scholar
Polubarinova-Kochina, P. Y. 1945 On motion of the contour of an oil layer. Dokl. Akad. Nauk SSSR 47, 254–257.Google Scholar
Polyanin, A. D. & Manzhirov, A. V. 2008 Handbook of Integral Equations, 2nd edn. Chapman and Hall/CRC.Google Scholar
Ruban, V. P. 2005 Quasiplanar steep water waves. Phys. Rev. E 71, 055303R.Google Scholar
Rudin, W. 1986 Real and Complex Analysis, 3rd edn. McGraw-Hill.Google Scholar
Shikin, V. B. 1970 Motion of helium ions near a vapor–liquid surface. Sov. Phys. JETP 31, 936.Google Scholar
Shraiman, B. I. & Bensimon, D. 1984 Singularities in nonlocal interface dynamics. Phys. Rev. A 30, 2840–2844.Google Scholar
Stoker, J. J. 1957 Water Waves. Interscience.Google Scholar
Stokes, G. G. 1880 On the theory of oscillatory waves. Math. Phys. Papers 1, 197–229.Google Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instability. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
Tanveer, S. 1993 Singularities in the classical Rayleigh–Taylor flow: formation and subsequent motion. Proc. R. Soc. Lond. A 441, 501–525.Google Scholar
Tanveer, S. 1996 Some analytical properties of solutions to a two-dimensional steadily translating inviscid bubble. Proc. R. Soc. Lond. A 452, 1397–1410.Google Scholar
Titchmarsh, E. C. 1948 Introduction to the Theory of Fourier Integrals, 2nd edn. Clarendon.Google Scholar
Weinstein, A. 1983 The local structure of Poisson manifolds. J. Differ. Geom. 18, 523–557.Google Scholar
Wilkening, J. 2011 Breakdown of self-similarity at the crests of large-amplitude standing water waves. Phys. Rev. Lett. 107, 184501.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on a surface. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.Google Scholar
Zakharov, V. E. & Dyachenko, A. I.2012 Free-surface hydrodynamics in the conformal variables. arXiv:1206.2046.Google Scholar
Zakharov, V. E., Dyachenko, A. I. & Prokofiev, A. O. 2006 Freak waves as nonlinear stage of Stokes wave modulation instability. Eur. J. Mech. (B/Fluids) 25, 677–692.Google Scholar
Zakharov, V. E., Dyachenko, A. I. & Vasiliev, O. A. 2002 New method for numerical simulation of nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. (B/Fluids) 21, 283–291.Google Scholar
Zakharov, V. E. & Faddeev, L. D. 1971 Korteweg–de Vries equation: a completely integrable Hamiltonian system. Funct. Anal. Applics. 5, 280–287.Google Scholar
Zakharov, V. E. & Kuznetsov, E. A. 1997 Hamiltonian formalism for nonlinear waves. Usp. Fiz. Nauk 167, 1137–1167.Google Scholar
Zakharov, V. E., Lvov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I. Springer.Google Scholar
Zakharov, V. E. & Shabat, A. B. 1972 Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62.Google Scholar
Zubarev, N. M. 2000 Charged-surface instability development in liquid helium: an exact solution. JETP Lett. 71, 367–369.Google Scholar
Zubarev, N. M. 2002 Exact solutions of the equations of motion of liquid helium with a charged free surface. J. Expl Theor. Phys. 94, 534–544.Google Scholar
Zubarev, N. M. 2008 Formation of singularities on the charged surface of a liquid-helium layer with a finite depth. J. Expl Theor. Phys. 107, 668–678.Google Scholar
Zubarev, N. M. & Kochurin, E. A. 2014 Interaction of strongly nonlinear waves on the free surface of a dielectric liquid in a horizontal electric field. JETP Lett. 99, 627–631.Google Scholar
Zubarev, N. M. & Zubareva, O. V. 2006 Nondispersive propagation of waves with finite amplitudes on the surface of a dielectric liquid in a tangential electric field. Tech. Phys. Lett. 32, 886–888.Google Scholar
Zubarev, N. M. & Zubareva, O. V. 2008 Stability of nonlinear waves on the ideal liquid surface in a tangential electric field. Tech. Phys. Lett. 34, 535–537.Google Scholar