 ${\it\alpha}$ fluctuations with non-zero correlation times
${\it\alpha}$ fluctuations with non-zero correlation timesPublished online by Cambridge University Press: 09 June 2016
We present a theory of large-scale dynamo action in a turbulent flow that has stochastic, zero-mean fluctuations of the  ${\it\alpha}$ parameter. Particularly interesting is the possibility of the growth of the mean magnetic field due to Moffatt drift, which is expected to be finite in a statistically anisotropic turbulence. We extend the Kraichnan–Moffatt model to explore effects of finite memory of
${\it\alpha}$ parameter. Particularly interesting is the possibility of the growth of the mean magnetic field due to Moffatt drift, which is expected to be finite in a statistically anisotropic turbulence. We extend the Kraichnan–Moffatt model to explore effects of finite memory of  ${\it\alpha}$ fluctuations, in a spirit similar to that of Sridhar & Singh (Mon. Not. R. Astron. Soc., vol. 445, 2014, pp. 3770–3787). Using the first-order smoothing approximation, we derive a linear integro-differential equation governing the dynamics of the large-scale magnetic field, which is non-perturbative in the
${\it\alpha}$ fluctuations, in a spirit similar to that of Sridhar & Singh (Mon. Not. R. Astron. Soc., vol. 445, 2014, pp. 3770–3787). Using the first-order smoothing approximation, we derive a linear integro-differential equation governing the dynamics of the large-scale magnetic field, which is non-perturbative in the  ${\it\alpha}$-correlation time
${\it\alpha}$-correlation time 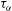 ${\it\tau}_{{\it\alpha}}$. We recover earlier results in the exactly solvable white-noise limit where the Moffatt drift does not contribute to the dynamo growth/decay. To study finite-memory effects, we reduce the integro-differential equation to a partial differential equation by assuming that
${\it\tau}_{{\it\alpha}}$. We recover earlier results in the exactly solvable white-noise limit where the Moffatt drift does not contribute to the dynamo growth/decay. To study finite-memory effects, we reduce the integro-differential equation to a partial differential equation by assuming that 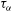 ${\it\tau}_{{\it\alpha}}$ be small but non-zero and the large-scale magnetic field is slowly varying. We derive the dispersion relation and provide an explicit expression for the growth rate as a function of four independent parameters. When
${\it\tau}_{{\it\alpha}}$ be small but non-zero and the large-scale magnetic field is slowly varying. We derive the dispersion relation and provide an explicit expression for the growth rate as a function of four independent parameters. When 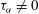 ${\it\tau}_{{\it\alpha}}\neq 0$, we find that: (i) in the absence of the Moffatt drift, but with finite Kraichnan diffusivity, only strong
${\it\tau}_{{\it\alpha}}\neq 0$, we find that: (i) in the absence of the Moffatt drift, but with finite Kraichnan diffusivity, only strong  ${\it\alpha}$ fluctuations can enable a mean-field dynamo (this is qualitatively similar to the white-noise case); (ii) in the general case when also the Moffatt drift is non-zero, both weak and strong
${\it\alpha}$ fluctuations can enable a mean-field dynamo (this is qualitatively similar to the white-noise case); (ii) in the general case when also the Moffatt drift is non-zero, both weak and strong  ${\it\alpha}$ fluctuations can lead to a large-scale dynamo; and (iii) there always exists a wavenumber (
${\it\alpha}$ fluctuations can lead to a large-scale dynamo; and (iii) there always exists a wavenumber (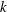 $k$) cutoff at some large
$k$) cutoff at some large 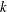 $k$ beyond which the growth rate turns negative, irrespective of weak or strong
$k$ beyond which the growth rate turns negative, irrespective of weak or strong  ${\it\alpha}$ fluctuations. Thus we show that a finite Moffatt drift can always facilitate large-scale dynamo action if sufficiently strong, even in the case of weak
${\it\alpha}$ fluctuations. Thus we show that a finite Moffatt drift can always facilitate large-scale dynamo action if sufficiently strong, even in the case of weak  ${\it\alpha}$ fluctuations, and the maximum growth occurs at intermediate wavenumbers.
${\it\alpha}$ fluctuations, and the maximum growth occurs at intermediate wavenumbers.