Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gajjar, P.
and
Gray, J. M. N. T.
2014.
Asymmetric flux models for particle-size segregation in granular avalanches.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
297.
Christov, Ivan C.
and
Stone, Howard A.
2014.
Shear dispersion in dense granular flows.
Granular Matter,
Vol. 16,
Issue. 4,
p.
509.
Hu, Kaiwei
Xie, Zi-Ang
Wu, Ping
Sun, Jing
Li, Li
Jia, Chao
Zhang, Shiping
Liu, Chuanping
and
Wang, Li
2014.
Convecting particle diffusion in a binary particle system under vertical vibration.
Soft Matter,
Vol. 10,
Issue. 24,
p.
4348.
Gray, John Mark Nicholas Timm
Gajjar, Parmesh
and
Kokelaar, Peter
2015.
Particle-size segregation in dense granular avalanches
.
Comptes Rendus. Physique,
Vol. 16,
Issue. 1,
p.
73.
Schlick, Conor P.
Fan, Yi
Umbanhowar, Paul B.
Ottino, Julio M.
and
Lueptow, Richard M.
2015.
Granular segregation in circular tumblers: theoretical model and scaling laws.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
632.
Ayeni, O.O.
Wu, C.L.
Joshi, J.B.
and
Nandakumar, K.
2015.
A discrete element method study of granular segregation in non-circular rotating drums.
Powder Technology,
Vol. 283,
Issue. ,
p.
549.
Fan, Yi
and
Hill, K. M.
2015.
Shear-induced segregation of particles by material density.
Physical Review E,
Vol. 92,
Issue. 2,
Marks, Benjy
and
Einav, Itai
2015.
A mixture of crushing and segregation: The complexity of grainsize in natural granular flows.
Geophysical Research Letters,
Vol. 42,
Issue. 2,
p.
274.
van der Vaart, K.
Gajjar, P.
Epely-Chauvin, G.
Andreini, N.
Gray, J. M. N. T.
and
Ancey, C.
2015.
Underlying Asymmetry within Particle Size Segregation.
Physical Review Letters,
Vol. 114,
Issue. 23,
Fan, Yi
Umbanhowar, Paul B.
Ottino, Julio M.
and
Lueptow, Richard M.
2015.
Shear-Rate-Independent Diffusion in Granular Flows.
Physical Review Letters,
Vol. 115,
Issue. 8,
Schlick, Conor P.
Fan, Yi
Isner, Austin B.
Umbanhowar, Paul B.
Ottino, Julio M.
and
Lueptow, Richard M.
2015.
Modeling segregation of bidisperse granular materials using physical control parameters in the quasi‐2D bounded heap.
AIChE Journal,
Vol. 61,
Issue. 5,
p.
1524.
Schlick, Conor P.
Isner, Austin B.
Umbanhowar, Paul B.
Lueptow, Richard M.
and
Ottino, Julio M.
2015.
On Mixing and Segregation: From Fluids and Maps to Granular Solids and Advection–Diffusion Systems.
Industrial & Engineering Chemistry Research,
Vol. 54,
Issue. 42,
p.
10465.
Larcher, Michele
and
Jenkins, James T.
2015.
The evolution of segregation in dense inclined flows of binary mixtures of spheres.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
405.
Schlick, Conor P.
Isner, Austin B.
Freireich, Ben J.
Fan, Yi
Umbanhowar, Paul B.
Ottino, Julio M.
and
Lueptow, Richard M.
2016.
A continuum approach for predicting segregation in flowing polydisperse granular materials.
Journal of Fluid Mechanics,
Vol. 797,
Issue. ,
p.
95.
Ren, Xinxin
Zhou, Guangzheng
Xu, Ji
Cui, Lijie
and
Ge, Wei
2016.
Numerical analysis of enhanced mixing in a Gallay tote blender.
Particuology,
Vol. 29,
Issue. ,
p.
95.
Sun, Jing
Liu, Chuanping
Wu, Ping
Xie, Zi-Ang
Hu, Kaiwei
and
Wang, Li
2016.
Granular core phenomenon induced by convection in a vertically vibrated cylindrical container.
Physical Review E,
Vol. 94,
Issue. 3,
Wiącek, J.
2016.
Geometrical parameters of binary granular mixtures with size ratio and volume fraction: experiments and DEM simulations.
Granular Matter,
Vol. 18,
Issue. 3,
Hill, Kimberly M.
and
Fan, Yi
2016.
Granular Temperature and Segregation in Dense Sheared Particulate Mixtures.
KONA Powder and Particle Journal,
Vol. 33,
Issue. 0,
p.
150.
Bertuola, Davide
Volpato, Silvia
Canu, Paolo
and
Santomaso, Andrea C.
2016.
Prediction of segregation in funnel and mass flow discharge.
Chemical Engineering Science,
Vol. 150,
Issue. ,
p.
16.
Khola, N.
and
Wassgren, C.
2016.
Correlations for shear-induced percolation segregation in granular shear flows.
Powder Technology,
Vol. 288,
Issue. ,
p.
441.
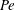 $\mathit{Pe}$, captures the interplay of advection and diffusion, and the second dimensionless parameter,
$\mathit{Pe}$, captures the interplay of advection and diffusion, and the second dimensionless parameter, 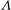 $\Lambda $, describes the interplay between segregation and advection. A parametric study of
$\Lambda $, describes the interplay between segregation and advection. A parametric study of 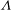 $\Lambda $ and
$\Lambda $ and 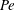 $\mathit{Pe}$ demonstrates how the particle segregation configuration depends on the interplay of advection, segregation and diffusion. The model can be readily adapted to other flow geometries.
$\mathit{Pe}$ demonstrates how the particle segregation configuration depends on the interplay of advection, segregation and diffusion. The model can be readily adapted to other flow geometries.