Published online by Cambridge University Press: 17 November 2016
The influence of near-wall density and viscosity gradients on near-wall turbulence in a channel is studied by means of direct numerical simulation of the low-Mach-number approximation of the Navier–Stokes equations. Different constitutive relations for density 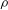 $\unicode[STIX]{x1D70C}$ and viscosity
$\unicode[STIX]{x1D70C}$ and viscosity  $\unicode[STIX]{x1D707}$ as a function of temperature are used in order to mimic a wide range of fluid behaviours and to develop a generalised framework for studying turbulence modulations in variable-property flows. Instead of scaling the velocity solely based on local density, as done for the van Driest transformation, we derive an extension of the scaling that is based on gradients of the semilocal Reynolds number, defined as
$\unicode[STIX]{x1D707}$ as a function of temperature are used in order to mimic a wide range of fluid behaviours and to develop a generalised framework for studying turbulence modulations in variable-property flows. Instead of scaling the velocity solely based on local density, as done for the van Driest transformation, we derive an extension of the scaling that is based on gradients of the semilocal Reynolds number, defined as 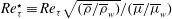 $Re_{\unicode[STIX]{x1D70F}}^{\star }\equiv Re_{\unicode[STIX]{x1D70F}}\sqrt{(\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w})}/(\overline{\unicode[STIX]{x1D707}}/\overline{\unicode[STIX]{x1D707}}_{w})$ (the bar and subscript
$Re_{\unicode[STIX]{x1D70F}}^{\star }\equiv Re_{\unicode[STIX]{x1D70F}}\sqrt{(\overline{\unicode[STIX]{x1D70C}}/\overline{\unicode[STIX]{x1D70C}}_{w})}/(\overline{\unicode[STIX]{x1D707}}/\overline{\unicode[STIX]{x1D707}}_{w})$ (the bar and subscript 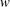 $w$ denote Reynolds averaging and wall value respectively, while
$w$ denote Reynolds averaging and wall value respectively, while 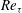 $Re_{\unicode[STIX]{x1D70F}}$ is the friction Reynolds number based on wall values). This extension of the van Driest transformation is able to collapse velocity profiles for flows with near-wall property gradients as a function of the semilocal wall coordinate. However, flow quantities like mixing length, turbulence anisotropy and turbulent vorticity fluctuations do not show a universal scaling very close to the wall. This is attributed to turbulence modulations, which play a crucial role in the evolution of turbulent structures and turbulence energy transfer. We therefore investigate the characteristics of streamwise velocity streaks and quasistreamwise vortices and find that, similarly to turbulence statistics, the turbulent structures are also strongly governed by
$Re_{\unicode[STIX]{x1D70F}}$ is the friction Reynolds number based on wall values). This extension of the van Driest transformation is able to collapse velocity profiles for flows with near-wall property gradients as a function of the semilocal wall coordinate. However, flow quantities like mixing length, turbulence anisotropy and turbulent vorticity fluctuations do not show a universal scaling very close to the wall. This is attributed to turbulence modulations, which play a crucial role in the evolution of turbulent structures and turbulence energy transfer. We therefore investigate the characteristics of streamwise velocity streaks and quasistreamwise vortices and find that, similarly to turbulence statistics, the turbulent structures are also strongly governed by  $Re_{\unicode[STIX]{x1D70F}}^{\star }$ profiles and that their dependence on individual density and viscosity profiles is minor. Flows with near-wall gradients in
$Re_{\unicode[STIX]{x1D70F}}^{\star }$ profiles and that their dependence on individual density and viscosity profiles is minor. Flows with near-wall gradients in 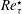 $Re_{\unicode[STIX]{x1D70F}}^{\star }$ (
$Re_{\unicode[STIX]{x1D70F}}^{\star }$ (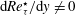 $\text{d}Re_{\unicode[STIX]{x1D70F}}^{\star }/\text{d}y\neq 0$) show significant changes in inclination and tilting angles of quasistreamwise vortices. These structural changes are responsible for the observed modulation of the Reynolds stress generation mechanism and the inter-component energy transfer in flows with strong near-wall
$\text{d}Re_{\unicode[STIX]{x1D70F}}^{\star }/\text{d}y\neq 0$) show significant changes in inclination and tilting angles of quasistreamwise vortices. These structural changes are responsible for the observed modulation of the Reynolds stress generation mechanism and the inter-component energy transfer in flows with strong near-wall 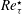 $Re_{\unicode[STIX]{x1D70F}}^{\star }$ gradients.
$Re_{\unicode[STIX]{x1D70F}}^{\star }$ gradients.