Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-10T05:32:25.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of large-scale motions on the frictional drag in a turbulent boundary layer

Published online by Cambridge University Press:  26 September 2017

Jinyul Hwang  and
Hyung Jin Sung Open the ORCID record for Hyung Jin Sung [Opens in a new window]
Jinyul Hwang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation data of a turbulent boundary layer (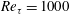$Re_{\unicode[STIX]{x1D70F}}=1000$) were used to investigate the large-scale influences on the vortical structures that contribute to the local skin friction. The amplitudes of the streamwise and wall-normal swirling strengths (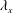$\unicode[STIX]{x1D706}_{x}$ and 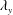$\unicode[STIX]{x1D706}_{y}$) were conditionally sampled by measuring the large-scale streamwise velocity fluctuations (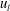$u_{l}$). In the near-wall region, the amplitudes of $\unicode[STIX]{x1D706}_{x}$ and 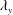$\unicode[STIX]{x1D706}_{y}$ decreased under negative $u_{l}$ rather than under positive 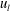$u_{l}$. This behaviour arose from the spanwise motions within the footprints of the large-scale low-speed (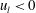$u_{l}<0$) and high-speed structures (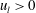$u_{l}>0$). The intense spanwise motions under the footprint of positive 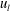$u_{l}$ noticeably strengthened the small-scale spanwise velocity fluctuations (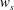$w_{s}$) below the centre of the near-wall vortical structures as compared to 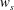$w_{s}$ within the footprint of negative 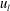$u_{l}$. The streamwise and wall-normal components were attenuated or amplified around the modulated vortical motions, which in turn led to the dependence of the swirling strength on the 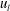$u_{l}$ event. We quantified the contribution of the modulated vortical motions 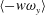$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$, which were related to a change-of-scale effect due to the vortex-stretching force, to the local skin friction. In the near-wall region, intense values of 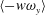$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ were observed for positive 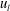$u_{l}$. By contrast, these values were low for negative 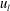$u_{l}$, in connection with the amplification of 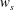$w_{s}$ and 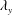$\unicode[STIX]{x1D706}_{y}$ by the strong spanwise motions of the positive 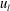$u_{l}$. The resultant skin friction induced by the amplified vortical motions within 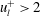$u_{l}^{+}>2$ was responsible for 15 % of the total skin friction generated by the change-of-scale effect. Finally, we applied this analysis to a drag-reduced flow and found that the amplified vortical motions within the footprint of positive 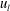$u_{l}$ were markedly diminished, which ultimately contributed to the total drag reduction.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 751 - 779
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Adrian, R. J., Christensen, K. T. & Liu, Z. C. 2000 Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29, 275–290.CrossRefGoogle Scholar
Agostini, L. & Leschziner, M. A. 2014 On the influence of outer large-scale structures on near-wall turbulence in channel flow. Phys. Fluids 26 (7), 075107.Google Scholar
Ahn, J., Lee, J. H., Jang, S. J. & Sung, H. J. 2013 Direct numerical simulations of fully developed turbulent pipe flows for Re 𝜏 = 180, 544 and 934. Intl J. Heat Fluid Flow 44, 222–228.CrossRefGoogle Scholar
Ahn, J., Lee, J. H., Lee, J., Kang, J.-H & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27 (6), 065110.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.CrossRefGoogle Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23 (6), 061701.CrossRefGoogle Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Chernyshenko, S. I., Marusic, I. & Mathis, R.2012 Quasi-steady description of modulation effects in wall turbulence. arXiv:1203.3714.Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.CrossRefGoogle Scholar
Chung, D., Monty, J. P. & Ooi, A. 2014 An idealised assessment of Townsend’s outer-layer similarly hypothesis for wall turbulence. J. Fluid Mech. 742, R3.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Fiscaletti, D., Ganapathisubramani, B. & Elsinga, G. E. 2015 Amplitude and frequency modulation of the small scales in a jet. J. Fluid Mech. 772, 756–783.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), 13–17.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high Reynolds number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Hwang, J., Lee, J. & Sung, H. J. 2016a Influence of large-scale accelerating motions on turbulent pipe and channel flows. J. Fluid Mech. 804, 420–441.CrossRefGoogle Scholar
Hwang, J., Lee, J., Sung, H. J. & Zaki, T. A. 2016b Inner-outer interactions of large-scale structures in turbulent channel flow. J. Fluid Mech. 790, 128–157.CrossRefGoogle Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.CrossRefGoogle Scholar
Liu, Z., Adrian, R. J. & Hanratty, T. J. 2001 Large-scale modes of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Chernyshenko, S. L. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 23, 021704.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010a Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010b Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.CrossRefGoogle Scholar
Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to Re 𝜃 = 2500 studied through simulation and experiment. Phys. Fluids 21 (5), 51702.CrossRefGoogle Scholar
Smits, A. J., Matheson, N. & Joubert, P. N. 1983 Low-Reynolds-number turbulent boundary layers in zero and favorable pressure gradients. J. Ship Res. 27, 147–157.CrossRefGoogle Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at R + = 685: large- and very large-scale motions. J. Fluid Mech. 698, 235–281.CrossRefGoogle Scholar
Yoon, M., Ahn, J., Hwang, J. & Sung, H. J. 2016a Contribution of velocity–vorticity correlations to the frictional drag in wall-bounded turbulent flows. Phys. Fluids 28 (8), 081702.CrossRefGoogle Scholar
Yoon, M., Hwang, J., Lee, J., Sung, H. J. & Kim, J. 2016b Large-scale motions in a turbulent channel flow with the slip boundary condition. Intl J. Heat Fluid Flow 61, 96–107.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar