Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T05:19:58.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Hollow vortex in a corner

Published online by Cambridge University Press:  07 December 2020

T. W. Christopher Open the ORCID record for T. W. Christopher [Opens in a new window]  and
Stefan G. Llewellyn Smith Open the ORCID record for Stefan G. Llewellyn Smith [Opens in a new window]
T. W. Christopher*
Affiliation:
Department of Mechanical and Aerospace Engineering, Jacobs School of Engineering, UCSD, 9500 Gilman Drive, La Jolla, CA92093-0411, USA
Stefan G. Llewellyn Smith
Affiliation:
Department of Mechanical and Aerospace Engineering, Jacobs School of Engineering, UCSD, 9500 Gilman Drive, La Jolla, CA92093-0411, USA Scripps Institution of Oceanography, UCSD, 9500 Gilman Drive, La Jolla, CA92093-0230, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

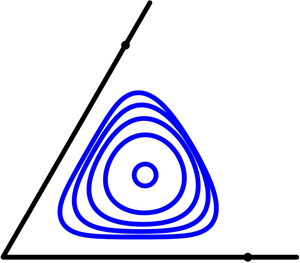
Equilibrium solutions for hollow vortices in straining flow in a corner are obtained by solving a free-boundary problem. Conformal maps from a canonical doubly connected annular domain to the physical plane combining the Schottky–Klein prime function with an appropriate algebraic map lead to a problem similar to Pocklington's propagating hollow dipole. The result is a two-parameter family of solutions depending on the corner angle and on the non-dimensional ratio of strain to circulation.

JFM classification

Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , R2
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baker, G. R. & Xie, C. 2011 Singularities in the complex physical plane for deep water waves. J. Fluid Mech. 685, 83–116.CrossRefGoogle Scholar
Crowdy, D. G. 2020 Solving Problems in Multiply Connected Domains. SIAM.CrossRefGoogle Scholar
Crowdy, D. G., Llewellyn Smith, S. G. & Freilich, D. V. 2013 Translating hollow vortex pairs. Eur. J. Mech. B/Fluids 37, 180–186.CrossRefGoogle Scholar
Deem, G. S. & Zabusky, N. J. 1978 Vortex waves: stationary “V states”, interactions, recurrence and breaking. Phys. Rev. Lett. 40, 859–862.CrossRefGoogle Scholar
Llewellyn Smith, S. G. 2014 Desingularized propagating vortex equilibria. Fluid Dyn. Res. 46, 061419.Google Scholar
Llewellyn Smith, S. G. & Crowdy, D. G. 2012 Structure and stability of hollow vortex equilibria. J. Fluid Mech. 691, 178–200.CrossRefGoogle Scholar
Michell, J. H. 1890 On the theory of free stream lines. Phil. Trans. R. Soc. Lond. A 181, 389–431.Google Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.Google Scholar
Pocklington, H. C. 1895 The configuration of a pair of equal and opposite hollow straight vortices of finite cross-section, moving steadily through the fluid. Proc. Camb. Phil. Soc. 8, 178–187.Google Scholar
Sadovskii, V. S. 1971 Vortex regions in a potential stream with a jump of Bernoulli's constant at the boundary. Z. Angew. Math. Mech. 35, 729–735.CrossRefGoogle Scholar
Saffman, P. G. & Tanveer, S. 1982 The touching pair of equal and opposite uniform vortices. Phys. Fluids 25, 1929–1930.CrossRefGoogle Scholar
Suh, Y. K. 1993 Periodic motion of a point vortex in a corner subject to a potential flow. J. Phys. Soc. Japan 62, 3441–3445.CrossRefGoogle Scholar
Tanveer, S. 1986 A steadily translating pair of equal and opposite vortices with vortex sheets on their boundaries. Stud. Appl. Maths 74, 139–154.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar