Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T00:17:14.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid–structure interaction of a square cylinder at different angles of attack

Published online by Cambridge University Press:  23 April 2014

Jisheng Zhao ,
Justin S. Leontini ,
David Lo Jacono  and
John Sheridan
Jisheng Zhao*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Vic 3800, Australia
Justin S. Leontini
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Vic 3800, Australia Department of Mechanical Engineering and Product Design Engineering, Swinburne University of Technology, John St Hawthorn, 3162, Australia
David Lo Jacono
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Vic 3800, Australia Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS, UPS, Université de Toulouse, Allée Camille Soula, F-31400 Toulouse, France
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Vic 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study investigates the free transverse flow-induced vibration (FIV) of an elastically mounted low-mass-ratio square cylinder in a free stream, at three different incidence angles: 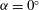${{\alpha }}=0^\circ $, 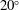$20^\circ $ and 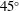$45^\circ $. This geometric setup presents a body with an angle of attack, sharp corners and some afterbody, and therefore is a generic body that can be used to investigate a wide range of FIV phenomena. A recent study by Nemes et al. (J. Fluid Mech., vol. 710, 2012, pp. 102–130) provided a broad overview of the flow regimes present as a function of both the angle of attack ${{\alpha }}$ and reduced flow velocity 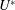${U^{*}}$. Here, the focus is on the three aforementioned representative angles of attack: 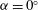${{\alpha }}=0^\circ $, where the FIV is dominated by transverse galloping; 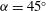${{\alpha }}=45^\circ $, where the FIV is dominated by vortex-induced vibration (VIV); and an intermediate value of 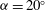${{\alpha }}=20^\circ $, where the underlying FIV phenomenon has previously been difficult to determine. For the 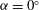${{\alpha }}=0^\circ $ case, the amplitude of oscillation increases linearly with the flow speed except for a series of regimes that occur when the vortex shedding frequency is in the vicinity of an odd-integer multiple of the galloping oscillation frequency, and the vortex shedding synchronizes to this multiple of the oscillation frequency. It is shown that only odd-integer multiple synchronizations should occur. These synchronizations explain the ‘kinks’ in the galloping amplitude response for light bodies first observed by Bearman et al. (J. Fluids Struct., vol. 1, 1987, pp. 19–34). For the 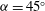${{\alpha }}=45^\circ $ case, the VIV response consists of a number of subtle, but distinctly different regimes, with five regimes of high-amplitude oscillations, compared to two found in the classic VIV studies of a circular cylinder. For the intermediate 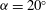${{\alpha }}=20^\circ $ case, a typical VIV ‘upper branch’ occurs followed by a ‘higher branch’ of very large-amplitude response. The higher branch is caused by a subharmonic synchronization between the vortex shedding and the body oscillation frequency, where two cycles of vortex shedding occur over one cycle of oscillation. It appears that this subharmonic synchronization is a direct result of the asymmetric body. Overall, the FIV of the square cylinder is shown to be very rich, with a number of distinct regimes, controlled by both ${{\alpha }}$ and 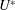${U^{*}}$. Importantly, ${{\alpha }}$ controls the underlying FIV phenomenon, as well as controlling the types of possible synchronization between the oscillation and vortex shedding.

JFM classification

Aerodynamics: Flow-structure interactions Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 688 - 721
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bearman, P. W., Gartshore, I. S., Maull, D. & Parkinson, G. V. 1987 Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1 (1), 19–34.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. 2nd edn Krieger.Google Scholar
Bokaian, A. R. & Geoola, F. 1984 Hydroelastic instabilities of square cylinders. J. Sound Vib. 92, 117–141.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2001 Force and wake modes of an oscillating cylinder. J. Fluids Struct. 15, 523–532.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.Google Scholar
Corless, R. & Parkinson, G. V. 1988 A model of the combined effects of vortex-induced oscillation and galloping. J. Fluids Struct. 2 (3), 203–220.Google Scholar
Corless, R. M. & Parkinson, G. V. 1993 Mathematical modelling of the combined effects of vortex-induced vibration and galloping. Part II. J. Fluids Struct. 7, 825–848.Google Scholar
Cvitanović, P., Shraiman, B. & Söderberg, B. 1985 Scaling laws for mode lockings in circle maps. Phys. Scr. 32 (4), 263–270.Google Scholar
Den Hartog, J. P. 1932 Transmission line vibration due to sleet. Trans. Am. Inst. Electr. Engrs 51 (4), 1074–1076.CrossRefGoogle Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Hahn, S. L. 1996 Hilbert Transforms in Signal Processing. Artech House.Google Scholar
Hover, F. S., Techet, A. H. & Triantafyllou, M. S. 1998 Forces on oscillating uniform and tapered cylinders in crossflow. J. Fluid Mech. 363, 97–114.CrossRefGoogle Scholar
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., Yen, N.-C., Tung, C. C. & Liu, H. H. 1998 The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 454 (1971), 903–995.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1996 Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 10 (5), 455–472.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1997 Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 11 (8), 973–982.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2011 A numerical study of an inline oscillating cylinder in a free stream. J. Fluid Mech. 688, 551–568.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2013 Wake states and frequency selection of a streamwise oscillating cylinder. J. Fluid Mech. 730, 162–192.Google Scholar
Leontini, J. S. & Thompson, M. C. 2013 Vortex-induced vibrations of a diamond cross-section: sensitivity to corner sharpness. J. Fluids Struct. 39, 371–390.CrossRefGoogle Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.Google Scholar
Morse, T. L. & Williamson, C. H. K. 2009 Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.Google Scholar
Naudascher, E. & Rockwell, D. 2005 Flow-Induced Vibrations: An Engineering Guide. Dover.Google Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Norberg, C. 2001 Flow around a circular cylinder: aspects of flucuating lift. J. Fluids Struct. 15, 459–469.CrossRefGoogle Scholar
Païdoussis, M. P., Price, S. & De Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Parkinson, G. V. & Smith, J. D. 1964 The square prism as an aeroelastic nonlinear oscillator. Q. J. Mech. Appl. Maths 17 (2), 225–239.CrossRefGoogle Scholar
Pomeau, Y. & Manneville, P. 1980 Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 74 (2), 189–197.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Sherry, M., Lo Jacono, D. & Sheridan, J. 2010 An experimental investigation of the recirculation zone formed downstream of a forward facing step. J. Wind Engng Ind. Aerodyn. 98 (12), 888–894.Google Scholar
Tudball-Smith, D., Leontini, J. S., Sheridan, J. & Lo Jacono, D. 2012 Streamwise forced oscillations of circular and square cylinders. Phys. Fluids 24, 111703.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibration. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2013 Numerical simulation of vortex-induced vibration of a square cylinder at low Reynolds number. Phys. Fluids 25, 023603.Google Scholar