Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T13:36:41.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluid injection into a confined porous layer

Published online by Cambridge University Press:  24 March 2014

Samuel S. Pegler ,
Herbert E. Huppert  and
Jerome A. Neufeld
Samuel S. Pegler*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Herbert E. Huppert
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Faculty of Science, University of Bristol, Bristol BS8 1UH, UK School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute and Department of Earth Sciences, Bullard Laboratories, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a theoretical and experimental study of viscous flows injected into a porous medium that is confined vertically by horizontal impermeable boundaries and filled with an ambient fluid of different density and viscosity. General three-dimensional equations describing such flows are developed, showing that the dynamics can be affected by two separate contributions: spreading due to gradients in hydrostatic pressure, and that due to the pressure drop introduced by the injection. In the illustrative case of a two-dimensional injection of fluid at a constant volumetric rate, the injected fluid initially forms a viscous gravity current insensitive both to the depth of the medium and to the viscosity of the ambient fluid. Beyond a characteristic time scale, the dynamics transition to being dominated by the injection pressure, and the injected fluid eventually intersects the second boundary to form a second moving contact line. Three different late-time asymptotic regimes can emerge, depending on whether the viscosity of the injected fluid is less than, equal to or greater than that of the ambient fluid. With a less viscous injection, the flow undergoes a slow decay towards a similarity solution in which the two contact lines extend linearly in time with differing prefactors. Perturbations from this long-term state are shown to decay algebraically with time. Equal viscosities result in both contact lines approaching the same leading-order asymptotic position but with a first-order correction to the distance between them that expands as 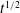$t^{1/2}$ due to gravitational spreading. For a more viscous injection, the distance between the contact lines approaches a constant value, with perturbations decaying exponentially. Data from a new series of laboratory experiments confirm these theoretical predictions.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 592 - 620
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover.Google Scholar
Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.CrossRefGoogle Scholar
Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics. Cambridge University Press.CrossRefGoogle Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bickle, M. J., Chadwick, R. A., Huppert, H. E., Hallworth, M. A. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.CrossRefGoogle Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected $\mathrm{CO}_{2}$ at the Sleipner field, North Sea. J. Geophys. Res. 117, B03309.Google Scholar
Chadwick, R. A., Zweigel, P., Gregersen, U., Kirby, G. A., Holloway, S. & Johannessen, P. N. 2004 Geological reservoir characterization of a $\mathrm{CO}_{2}$ storage site: the Utsira Sand, Sleipner, northern North Sea. Energy 29, 1371–1381.CrossRefGoogle Scholar
Dake, L. P. 2010 Fundamentals of Reservoir Engineering. (Developments in Petroleum Science), vol. 8. Elsevier.Google Scholar
Golding, M. J. & Huppert, H. E. 2010 The effect of confining impermeable boundaries on gravity currents in a porous medium. J. Fluid Mech. 649, 1–17.CrossRefGoogle Scholar
Grundy, R. E. & McLaughlin, R. 1982 Eigenvalues of the Barenblatt–Pattle similarity solution in nonlinear diffusion. Proc. R. Soc. Lond. A 649, 89–100.Google Scholar
Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.Google Scholar
Gunn, I. & Woods, A. W. 2012 On the flow of buoyant fluid injected into an aquifer with a background flow. J. Fluid Mech. 706, 274–294.Google Scholar
Hesse, M. A., Orr, F. M. Jr & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.CrossRefGoogle Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. Jr. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.CrossRefGoogle Scholar
Huppert, H. E. 1986 The intrusion of fluid mechanics into geology. J. Fluid Mech. 173, 557–594.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
MacMinn, C. W. & Juanes, R. 2009 Post-injection spreading and trapping of $\mathrm{CO}_{2}$ in saline aquifers: impact of the plume shape at the end of injection. Comput. Geosci. 13, 480–491.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2010 $\mathrm{CO}_{2}$ migration in saline aquifers. Part 1: Capillary trapping under slope and groundwater flow. J. Fluid Mech. 662, 329–351.CrossRefGoogle Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2011 $\mathrm{CO}_{2}$ migration in saline aquifers. Part 2: Combined capillary and solubility trapping. J. Fluid Mech. 688, 321–351.Google Scholar
Mathunjwa, J. S. & Hogg, A. J. 2006 Self-similar gravity currents in porous media: linear stability of the Barenblatt–Pattle solution revisited. Eur. J. Mech. (B/Fluids) 25, 360–378.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
Orr, F. M. Jr. 2009 Onshore geological storage of $\mathrm{CO}_{2}$. Science 325, 1656–1658.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2013a Topographic controls on gravity currents in porous media. J. Fluid Mech. 734, 317–337.Google Scholar
Pegler, S. S., Kowal, K. N., Hasenclever, L. Q. & Worster, M. G. 2013b Lateral controls on grounding-line dynamics. J. Fluid Mech. 722, R1.Google Scholar
Pegler, S. S., Lister, J. R. & Worster, M. G. 2012 Release of a viscous power-law fluid over an inviscid ocean. J. Fluid Mech. 700, 261–281.Google Scholar
Saffman, P. G. & Taylor, G. I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–329.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Vasco, D. W., Rucci, A., Ferretti, A., Novali, F., Bissell, R. C., Ringrose, P. S., Mathieson, A. S. & Wright, I. W. 2010 Satellite-based measurements of surface deformation reveal fluid flow associated with the geological storage of carbon dioxide. Geophys. Res. Lett. 37, L03303.Google Scholar
Vella, D. & Huppert, H. E. 2006 Gravity currents in a porous medium at an inclined plane. J. Fluid Mech. 555, 353–362.CrossRefGoogle Scholar
Woods, A. W. & Mason, R. 2000 The dynamics of two-layer gravity-driven flows in permeable rock. J. Fluid Mech. 421, 83–114.CrossRefGoogle Scholar