Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T05:07:10.371Z Has data issue: false hasContentIssue false
  • English
  • Français

Fingering instability in adhesion fronts

Published online by Cambridge University Press:  06 October 2022

M. L'Estimé ,
L. Duchemin Open the ORCID record for L. Duchemin [Opens in a new window] ,
É. Reyssat Open the ORCID record for É. Reyssat [Opens in a new window]  and
J. Bico Open the ORCID record for J. Bico [Opens in a new window]
M. L'Estimé
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH), CNRS, ESPCI Paris, Université PSL, Sorbonne Université, Université de Paris, Paris, France
L. Duchemin
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH), CNRS, ESPCI Paris, Université PSL, Sorbonne Université, Université de Paris, Paris, France
É. Reyssat
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH), CNRS, ESPCI Paris, Université PSL, Sorbonne Université, Université de Paris, Paris, France
J. Bico*
Affiliation:
Laboratoire de Physique et Mécanique des Milieux Hétérogènes (PMMH), CNRS, ESPCI Paris, Université PSL, Sorbonne Université, Université de Paris, Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

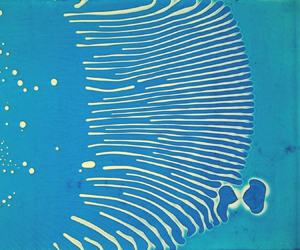
The adhesion of two surfaces relies on the propagation of an adhesion front. What is the dynamics of the front when both surfaces are coated with a thin layer of viscous liquid? Standard criteria from fingering instabilities would predict a stable front since viscous fluid pushes away air of low viscosity. Surprisingly, the front propagation may be unstable and generally leads to growing fingers. We demonstrate with model experiments where the two adhering surfaces are slightly tilted by an angle $\alpha$ that the origin of this interfacial instability relies on feeding the front from the surrounding thin film. We show experimentally that the typical wavelength of the instability is mainly dictated by the thickness of the oil layers $h$. In this wedge geometry, the propagation dynamics is found to follow a $t^{1/2}$ dependence and to saturate for an extension length of the order of $h/\alpha$.

JFM classification

Interfacial Flows (free surface): Fingering instability Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A46
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adda-Bedia, M. & Mahadevan, L. 2006 Crack-front instability in a confined elastic film. Proc. R. Soc. Lond. A 462 (2075), 3233–3251.Google Scholar
Al-Housseiny, T.T., Tsai, P.A. & Stone, H.A. 2012 Control of interfacial instabilities using flow geometry. Nat. Phys. 8 (10), 747–750.CrossRefGoogle Scholar
Ben-Jacob, E., Godbey, R., Goldenfeld, N.D., Koplik, J., Levine, H., Mueller, T. & Sander, L.M. 1985 Experimental demonstration of the role of anisotropy in interfacial pattern formation. Phys. Rev. Lett. 55 (12), 1315–1318.CrossRefGoogle ScholarPubMed
Biggins, J.S., Saintyves, B., Wei, Z., Bouchaud, E. & Mahadevan, L. 2013 Digital instability of a confined elastic meniscus. Proc. Natl Acad. Sci. USA 110 (31), 12545–12548.CrossRefGoogle ScholarPubMed
Bonn, D. & Meunier, J. 1997 Viscoelastic free-boundary problems: non-Newtonian viscosity vs normal stress effects. Phys. Rev. Lett. 79 (14), 2662–2665.CrossRefGoogle Scholar
Chiche, A., Dollhofer, J. & Creton, C. 2005 Cavity growth in soft adhesives. Eur. Phys. J. E 17 (4), 389–401.CrossRefGoogle ScholarPubMed
Courrech du Pont, S. & Eggers, J. 2020 Fluid interfaces with very sharp tips in viscous flow. Proc. Natl Acad. Sci. USA 117 (51), 32238–32243.CrossRefGoogle ScholarPubMed
Creton, C. & Ciccotti, M. 2016 Fracture and adhesion of soft materials: a review. Rep. Prog. Phys. 79 (4), 046601.CrossRefGoogle ScholarPubMed
Davis-Purcell, B., Soulard, P., Salez, T., Raphaël, E. & Dalnoki-Veress, K. 2018 Adhesion-induced fingering instability in thin elastic films under strain. Eur. Phys. J. E 41 (3), 1–7.CrossRefGoogle ScholarPubMed
Divoux, T., Shukla, A., Marsit, B., Kaloga, Y. & Bischofberger, I. 2020 Criterion for fingering instabilities in colloidal gels. Phys. Rev. Lett. 124 (24), 248006.CrossRefGoogle ScholarPubMed
Fermigier, M., Limat, L., Wesfreid, J.E., Boudinet, P. & Quilliet, C. 1992 Two-dimensional patterns in Rayleigh–Taylor instability of a thin layer. J. Fluid Mech. 236, 349–383.CrossRefGoogle Scholar
Ghatak, A. & Chaudhury, M.K. 2003 Adhesion-induced instability patterns in thin confined elastic film. Langmuir 19 (7), 2621–2631.CrossRefGoogle Scholar
Ghatak, A., Chaudhury, M.K., Shenoy, V. & Sharma, A. 2000 Meniscus instability in a thin elastic film. Phys. Rev. Lett. 85 (20), 4329–4332.CrossRefGoogle Scholar
Guillot, P., Ajdari, A., Goyon, J., Joanicot, M. & Colin, A. 2009 Droplets and jets in microfluidic devices. C. R. Chim. 12 (1), 247–257.CrossRefGoogle Scholar
Hashimoto, M., Garstecki, P., Stone, H.A. & Whitesides, G.M. 2008 Interfacial instabilities in a microfluidic hele-shaw cell. Soft Matt. 4, 1403–1413.CrossRefGoogle Scholar
Joseph, D.D., Nelson, J., Renardy, M. & Renardy, Y. 1991 Two-dimensional cusped interfaces. J. Fluid Mech. 223, 383–409.CrossRefGoogle Scholar
Keiser, L., Herbaut, R., Bico, J. & Reyssat, E. 2016 Washing wedges: capillary instability in a gradient of confinement. J. Fluid Mech. 790, 619–633.CrossRefGoogle Scholar
Lindner, A., Coussot, P. & Bonn, D. 2000 Viscous fingering in a yield stress fluid. Phys. Rev. Lett. 85 (2), 314–317.CrossRefGoogle Scholar
Lorenceau, E., Restagno, F. & Quéré, D. 2003 Fracture of a viscous liquid. Phys. Rev. Lett. 90 (18), 184501.CrossRefGoogle ScholarPubMed
McCloud, K.V. & Maher, J.V. 1995 Experimental perturbations to Saffman–Taylor flow. Phys. Rep. 260 (3), 139–185.CrossRefGoogle Scholar
Mönch, W. & Herminghaus, S. 2001 Elastic instability of rubber films between solid bodies. Europhys. Lett. 53 (4), 525–531.CrossRefGoogle Scholar
Nase, J., Lindner, A. & Creton, C. 2008 Pattern formation during deformation of a confined viscoelastic layer: from a viscous liquid to a soft elastic solid. Phys. Rev. Lett. 101 (7), 074503.CrossRefGoogle ScholarPubMed
Pearson, J.R.A. 1960 The instability of uniform viscous flow under rollers and spreaders. J. Fluid Mech. 7 (4), 481–500.CrossRefGoogle Scholar
Pelcé, P. 2012 Théorie des formes de croissance. EDP Sciences.Google Scholar
Pitts, E. & Greiller, J. 1961 The flow of thin liquid films between rollers. J. Fluid Mech. 11 (1), 33–50.CrossRefGoogle Scholar
Rabaud, M. 1994 Dynamiques interfaciales dans l'instabilité de l'imprimeur. Ann. Phys. France 19, 659–690.CrossRefGoogle Scholar
Rabaud, M., Couder, Y. & Michalland, S. 1991 Wavelength selection and transients in the one-dimensional array of cells of the printer's instability. Eur. J. Mech. B 10, 253–260.Google Scholar
Rauseo, S.N., Barnes, P.D. Jr. & Maher, J.V. 1987 Development of radial fingering patterns. Phys. Rev. A 35 (3), 1245–1251.CrossRefGoogle ScholarPubMed
Reyssat, E. 2014 Drops and bubbles in wedges. J. Fluid Mech. 748, 641–662.CrossRefGoogle Scholar
Roy, S. & Tarafdar, S. 1996 Patterns in the variable hele-shaw cell for different viscosity ratios: similarity to river network geometry. Phys. Rev. E 54 (6), 6495–6499.CrossRefGoogle ScholarPubMed
Saffman, P.G. & Taylor, G.I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245 (1242), 312–329.Google Scholar
Zeng, H., Tian, Y., Zhao, B., Tirrell, M. & Israelachvili, J. 2007 a Transient interfacial patterns and instabilities associated with liquid film adhesion and spreading. Langmuir 23 (11), 6126–6135.CrossRefGoogle ScholarPubMed
Zeng, H., Tian, Y., Zhao, B., Tirrell, M. & Israelachvili, J. 2007 b Transient surface patterns and instabilities at adhesive junctions of viscoelastic films. Macromolecules 40 (23), 8409–8422.CrossRefGoogle Scholar
Zeng, H., Zhao, B., Tian, Y., Tirrell, M., Leal, L.G. & Israelachvili, J.N. 2006 Transient surface patterns during adhesion and coalescence of thin liquid films. Soft Matt. 3 (1), 88–93.CrossRefGoogle ScholarPubMed
Zik, O. & Moses, E. 1999 Fingering instability in combustion: an extended view. Phys. Rev. E 60 (1), 518–531.CrossRefGoogle Scholar
Zik, O., Olami, Z. & Moses, E. 1998 Fingering instability in combustion. Phys. Rev. Lett. 81 (18), 3868–3871.CrossRefGoogle Scholar

L'Estimé et al. Supplementary Movie 1

See "L'Estimé et al. Supplementary Movie Captions"

Download L'Estimé et al. Supplementary Movie 1(Video)
Video 3.7 MB

L'Estimé et al. Supplementary Movie 2

See "L'Estimé et al. Supplementary Movie Captions"

Download L'Estimé et al. Supplementary Movie 2(Video)
Video 4.6 MB
Supplementary material: PDF

L'Estimé et al. Supplementary Movie Captions

L'Estimé et al. Supplementary Movie Captions

Download L'Estimé et al. Supplementary Movie Captions(PDF)
PDF 93.1 KB