Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T15:32:52.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Film thickness distribution in gravity-driven pancake-shaped droplets rising in a Hele-Shaw cell

Published online by Cambridge University Press:  15 July 2019

Isha Shukla Open the ORCID record for Isha Shukla [Opens in a new window] ,
Nicolas Kofman ,
Gioele Balestra Open the ORCID record for Gioele Balestra [Opens in a new window] ,
Lailai Zhu Open the ORCID record for Lailai Zhu [Opens in a new window]  and
François Gallaire Open the ORCID record for François Gallaire [Opens in a new window]
Isha Shukla
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
Nicolas Kofman
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
Gioele Balestra
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
Lailai Zhu
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
François Gallaire*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study here experimentally, numerically and using a lubrication approach, the shape, velocity and lubrication film thickness distribution of a droplet rising in a vertical Hele-Shaw cell. The droplet is surrounded by a stationary immiscible fluid and moves purely due to buoyancy. A low density difference between the two media helps to operate in a regime with capillary number 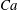$Ca$ lying between 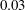$0.03$ and 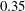$0.35$, where 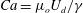$Ca=\unicode[STIX]{x1D707}_{o}U_{d}/\unicode[STIX]{x1D6FE}$ is built with the surrounding oil viscosity 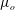$\unicode[STIX]{x1D707}_{o}$, the droplet velocity 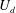$U_{d}$ and surface tension 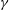$\unicode[STIX]{x1D6FE}$. The experimental data show that in this regime the droplet velocity is not influenced by the thickness of the thin lubricating film and the dynamic meniscus. For iso-viscous cases, experimental and three-dimensional numerical results of the film thickness distribution agree well with each other. The mean film thickness is well captured by the Aussillous & Quéré (Phys. Fluids, vol. 12 (10), 2000, pp. 2367–2371) model with fitting parameters. The droplet also exhibits the ‘catamaran’ shape that has been identified experimentally for a pressure-driven counterpart (Huerre et al., Phys. Rev. Lett., vol. 115 (6), 2015, 064501). This pattern has been rationalized using a two-dimensional lubrication equation. In particular, we show that this peculiar film thickness distribution is intrinsically related to the anisotropy of the fluxes induced by the droplet’s motion.

JFM classification

Drops and Bubbles: Drops Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 1021 - 1040
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atasi, O., Haut, B., Dehaeck, S., Dewandre, A., Legendre, D. & Scheid, B. 2018 How to measure the thickness of a lubrication film in a pancake bubble with a single snapshot? Appl. Phys. Lett. 113 (17), 173701.Google Scholar
Aussillous, P. & Quéré, D. 2000 Quick deposition of a fluid on the wall of a tube. Phys. Fluids 12 (10), 2367–2371.Google Scholar
Balestra, G.2018 Pattern formation in thin liquid films: from coating-flow instabilities to microfluidic droplets. PhD thesis, EPFL, Lausanne.Google Scholar
Balestra, G., Zhu, L. & Gallaire, F. 2018 Viscous Taylor droplets in axisymmetric and planar tubes: from Bretherton’s theory to empirical models. Microfluid. Nanofluid. 22 (6), 67.Google Scholar
Baroud, C. N., Gallaire, F. & Dangla, R. 2010 Dynamics of microfluidic droplets. Lab on a Chip 10 (16), 2032–2045.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.Google Scholar
Burgess, D. & Foster, M. R. 1990 Analysis of the boundary conditions for a Hele-Shaw bubble. Phys. Fluids A 2 (7), 1105–1117.Google Scholar
Bush, J. W. M. 1997 The anomalous wake accompanying bubbles rising in a thin gap: a mechanically forced Marangoni flow. J. Fluid Mech. 352, 283–303.Google Scholar
Daniel, D., Timonen, J. V. I., Li, R., Velling, S. J. & Aizenberg, J. 2017 Oleoplaning droplets on lubricated surfaces. Nat. Phys. 13 (10), 1020–1025.Google Scholar
Derjaguin, B. V. C. R. 1943 Thickness of liquid layer adhering to walls of vessels on their emptying and the theory of photo- and motion-picture film coating. C. R. (Dokl.) Acad. Sci. URSS 39, 13–16.Google Scholar
Eri, A. & Okumura, K. 2011 Viscous drag friction acting on a fluid drop confined in between two plates. Soft Matt. 7 (12), 5648–5653.Google Scholar
Farajzadeh, R., Andrianov, A. & Zitha, P. L. J. 2009 Investigation of immiscible and miscible foam for enhancing oil recovery. Ind. Engng Chem. Res. 49 (4), 1910–1919.Google Scholar
Gallaire, F., Meliga, P., Laure, P. & Baroud, C. N. 2014 Marangoni induced force on a drop in a Hele-Shaw cell. Phys. Fluids 26 (6), 062105.Google Scholar
Halpern, D. & Secomb, T. W. 1992 The squeezing of red blood cells through parallel-sided channels with near-minimal widths. J. Fluid Mech. 244, 307–322.Google Scholar
He, M., Edgar, J. S., Jeffries, G. D. M., Lorenz, R. M., Shelby, J. P. & Chiu, D. T. 2005 Selective encapsulation of single cells and subcellular organelles into picoliter- and femtoliter-volume droplets. Anal. Chem. 77 (6), 1539–1544.Google Scholar
Hodges, S. R., Jensen, O. E. & Rallison, J. M. 2004 Sliding, slipping and rolling: the sedimentation of a viscous drop down a gently inclined plane. J. Fluid Mech. 512, 95–131.Google Scholar
Huerre, A., Theodoly, O., Leshansky, A. M., Valignat, M.-P., Cantat, I. & Jullien, M.-C. 2015 Droplets in microchannels: dynamical properties of the lubrication film. Phys. Rev. Lett. 115 (6), 064501.Google Scholar
Kandlikar, S. G. 2012 History, advances, and challenges in liquid flow and flow boiling heat transfer in microchannels: a critical review. J. Heat Transfer 134 (3), 034001.Google Scholar
Keiser, L., Jaafar, K., Bico, J. & Reyssat, É. 2018 Dynamics of non-wetting drops confined in a Hele-Shaw cell. J. Fluid Mech. 845, 245–262.Google Scholar
Klaseboer, E., Gupta, R. & Manica, R. 2014 An extended Bretherton model for long Taylor bubbles at moderate capillary numbers. Phys. Fluids 26 (3), 032107.Google Scholar
Lamb, H. 1993 Hydrodynamics. Cambridge University Press.Google Scholar
Lamstaes, C. & Eggers, J. 2017 Arrested bubble rise in a narrow tube. J. Stat. Phys. 167 (3–4), 656–682.Google Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. URSS 17 (42), 42–54.Google Scholar
Lhuissier, H., Tagawa, Y., Tran, T. & Sun, C. 2013 Levitation of a drop over a moving surface. J. Fluid Mech. 733, R4.Google Scholar
Ling, Y., Fullana, J.-M., Popinet, S. & Josserand, C. 2016 Droplet migration in a Hele-Shaw cell: effect of the lubrication film on the droplet dynamics. Phys. Fluids 28 (6), 062001.Google Scholar
Magnini, M., Pulvirenti, B. & Thome, J. R. 2013 Numerical investigation of hydrodynamics and heat transfer of elongated bubbles during flow boiling in a microchannel. Intl J. Heat Mass Transfer 59, 451–471.Google Scholar
Martinez, M. J. & Udell, K. S. 1990 Axisymmetric creeping motion of drops through circular tubes. J. Fluid Mech. 210, 565–591.Google Scholar
Maxworthy, T. 1986 Bubble formation, motion and interaction in a Hele-Shaw cell. J. Fluid Mech. 173, 95–114.Google Scholar
Meiburg, E. 1989 Bubbles in a Hele-Shaw cell: numerical simulation of three-dimensional effects. Phys. Fluids A 1 (6), 938–946.Google Scholar
Nagel, M.2014 Modeling droplets flowing in microchannels. PhD thesis, EPFL, Lausanne.Google Scholar
Okumura, K. 2018 Viscous dynamics of drops and bubbles in Hele-Shaw cells: drainage, drag friction, coalescence, and bursting. Adv. Colloid Interface Sci. 255, 64–75.Google Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931.Google Scholar
Park, C. W. & Homsy, G. M. 1984 Two-phase displacement in Hele-Shaw cells: theory. J. Fluid Mech. 139, 291–308.Google Scholar
Reichert, B., Huerre, A., Theodoly, O., Valignat, M.-P., Cantat, I. & Jullien, M.-C. 2018 Topography of the lubrication film under a pancake droplet travelling in a Hele-Shaw cell. J. Fluid Mech. 850, 708–732.Google Scholar
Reyssat, E. 2014 Drops and bubbles in wedges. J. Fluid Mech. 748, 641–662.Google Scholar
Song, H., Chen, D. L. & Ismagilov, R. F. 2006 Reactions in droplets in microfluidic channels. Angew. Chem. Intl Ed. Engl. 45 (44), 7336–7356.Google Scholar
Stokes, G. G. 1898 Mathematical proof of the identity of the stream lines obtained by means of a viscous film with those of a perfect fluid moving in two dimensions. In Report of the Sixty-Eighth Meeting of the British Association for the Advancement of Science, pp. 143–144.Google Scholar
Tanveer, S. 1986 The effect of surface tension on the shape of a Hele-Shaw cell bubble. Phys. Fluids 29 (11), 3537–3548.Google Scholar
Taylor, G. I. & Saffman, P. G. 1959 A note on the motion of bubbles in a Hele-Shaw cell and porous medium. J. Mech. Appl. Maths 12 (3), 265–279.Google Scholar
Taylor, G. I. 1961 Deposition of a viscous fluid on the wall of a tube. J. Fluid Mech. 10 (2), 161–165.Google Scholar
Yahashi, M., Kimoto, N. & Okumura, K. 2016 Scaling crossover in thin-film drag dynamics of fluid drops in the Hele-Shaw cell. Sci. Rep. 6, 31395.Google Scholar
Yu, Y. E., Zhu, L., Shim, S., Eggers, J. & Stone, H. A. 2018 Time-dependent motion of a confined bubble in a tube: transition between two steady states. J. Fluid Mech. 857, R4.Google Scholar
Zhu, L. & Gallaire, F. 2016 A pancake droplet translating in a Hele-Shaw cell: lubrication film and flow field. J. Fluid Mech. 798, 955–969.Google Scholar