Hostname: page-component-7bb8b95d7b-cx56b Total loading time: 0 Render date: 2024-09-19T18:49:08.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of three-dimensional Rayleigh–Taylor instability of a gaseous interface

Published online by Cambridge University Press:  18 September 2024

Yu Liang Open the ORCID record for Yu Liang [Opens in a new window] ,
Ahmed Alkindi ,
Khalid Alzeyoudi ,
Lili Liu ,
Mohamed Ali Open the ORCID record for Mohamed Ali [Opens in a new window]  and
Nader Masmoudi
Yu Liang*
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE
Ahmed Alkindi
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE
Khalid Alzeyoudi
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE
Lili Liu
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE
Mohamed Ali
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE
Nader Masmoudi
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi 129188, UAE Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

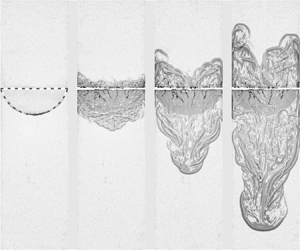
Validating the theoretical work on Rayleigh–Taylor instability (RTI) through experiments with an exceptionally clean and well-characterized initial condition has been a long-standing challenge. Experiments were conducted to study the three-dimensional RTI of an SF$_6$–air interface at moderate Atwood numbers. A novel soap film technique was developed to create a discontinuous gaseous interface with controllable initial conditions. Spectrum analysis revealed that the initial perturbation of the soap film interface is half the size of an entire single-mode perturbation. The correlation between the initial interface perturbation and Atwood numbers was determined. Due to the steep and highly curved feature of the initial soap film interface, the early-time evolution of RTI exhibits significant nonlinearity. In the quasi-steady regime, various potential flow models accurately predict the late-time bubble velocities by considering the channel width as the perturbation wavelength. Differently, the late-time spike velocities are described by these potential flow models using the wavelength of the entire single-mode perturbation. These findings indicate that the bubble evolution is influenced primarily by the spatial constraint imposed by walls, while the spike evolution is influenced mainly by the initial curvature of the spike tip. Consequently, a recent potential flow model was adopted to describe the time-varying amplitude growth induced by RTI. Furthermore, the self-similar growth factors for bubbles and spikes were determined from experiments and compared with existing studies, revealing that a large amplitude in the initial soap film interface promotes the spike development.

JFM classification

Convection: Buoyancy-driven instability Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 994 , 10 September 2024 , A7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abarzhi, S.I., Nishihara, K. & Glimm, J. 2003 Rayleigh–Taylor and Richtmyer–Meshkov instabilities for fluids with a finite density ratio. Phys. Lett. A 317 (5–6), 470–476.CrossRefGoogle Scholar
Akula, B. & Ranjan, D. 2016 Dynamics of buoyancy-driven flows at moderately high Atwood numbers. J. Fluid Mech. 795, 313–355.CrossRefGoogle Scholar
Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420 (6915), 479–481.CrossRefGoogle ScholarPubMed
Arnett, D. 2000 The role of mixing in astrophysics. Astrophys. J. Suppl. Ser. 127 (2), 213.CrossRefGoogle Scholar
Banerjee, A. 2020 Rayleigh–Taylor instability: a status review of experimental designs and measurement diagnostics. Trans. ASME J. Fluids Engng 142 (12), 120801.CrossRefGoogle Scholar
Banerjee, A., Kraft, W.N. & Andrews, M.J. 2010 Detailed measurements of a statistically steady Rayleigh–Taylor mixing layer from small to high Atwood numbers. J. Fluid Mech. 659, 127–190.CrossRefGoogle Scholar
Betti, R. & Hurricane, O.A. 2016 Inertial-confinement fusion with lasers. Nat. Phys. 12 (5), 435–448.CrossRefGoogle Scholar
Bian, X., Aluie, H., Zhao, D., Zhang, H. & Livescu, D. 2020 Revisiting the late-time growth of single-mode Rayleigh–Taylor instability and the role of vorticity. Physica D 403, 132250.CrossRefGoogle Scholar
Boffetta, G. & Mazzino, A. 2017 Incompressible Rayleigh–Taylor turbulence. Annu. Rev. Fluid Mech. 49, 119–143.CrossRefGoogle Scholar
Cabot, W. & Zhou, Y. 2013 Statistical measurements of scaling and anisotropy of turbulent flows induced by Rayleigh–Taylor instability. Phys. Fluids 25 (1), 015107.CrossRefGoogle Scholar
Cabot, W.H. & Cook, A.W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type Ia supernovae. Nat. Phys. 2 (8), 562–568.CrossRefGoogle Scholar
Cook, A.W. & Dimotakis, P.E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.CrossRefGoogle Scholar
Couder, Y., Chomaz, J.M. & Rabaud, M. 1989 On the hydrodynamics of soap films. Physica D 37 (1–3), 384–405.CrossRefGoogle Scholar
Dalziel, S.B., Linden, P.F. & Youngs, D.L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.CrossRefGoogle Scholar
Dimonte, G. 2000 Spanwise homogeneous buoyancy-drag model for Rayleigh–Taylor mixing and experimental evaluation. Phys. Plasmas 7, 2255–2269.CrossRefGoogle Scholar
Dimonte, G. 2004 Dependence of turbulent Rayleigh–Taylor instability on initial perturbations. Phys. Rev. E 69 (5), 056305.CrossRefGoogle ScholarPubMed
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.CrossRefGoogle Scholar
Duff, R.E., Harlow, F.H. & Hirt, C.W. 1962 Effects of diffusion on interface instability between gases. Phys. Fluids 5 (4), 417–425.CrossRefGoogle Scholar
Goncharov, V.N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.CrossRefGoogle ScholarPubMed
Guo, W. & Zhang, Q. 2020 Universality and scaling laws among fingers at Rayleigh–Taylor and Richtmyer–Meshkov unstable interfaces in different dimensions. Physica D 403, 132304.CrossRefGoogle Scholar
Huang, Z., De Luca, A., Atherton, T.J., Bird, M., Rosenblatt, C. & Carles, P. 2007 Rayleigh–Taylor instability experiments with precise and arbitrary control of the initial interface shape. Phys. Rev. Lett. 99 (20), 204502.CrossRefGoogle ScholarPubMed
Jacobs, J.W. & Catton, I. 1988 Three-dimensional Rayleigh–Taylor instability. Part 2. Experiment. J. Fluid Mech. 187, 353–371.CrossRefGoogle Scholar
Kucherenko, Y.A., Shibarshov, L.I., Chitaikin, V.I., Balabin, S.I. & Pylaev, A.P. 1991 Experimental study of the gravitational turbulent mixing self-similar mode. In 3rd International Workshop on the Physics of Compressible Turbulent Mixing, pp. 427–454. Cambridge University Press.Google Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1–12.CrossRefGoogle Scholar
Lewis, D.J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A 202 (1068), 81–96.Google Scholar
Liang, Y., Liu, L., Zhai, Z., Ding, J., Si, T. & Luo, X. 2021 Richtmyer–Meshkov instability on two-dimensional multi-mode interfaces. J. Fluid Mech. 928, A37.CrossRefGoogle Scholar
Liang, Y., Zhai, Z., Ding, J. & Luo, X. 2019 Richtmyer–Meshkov instability on a quasi-single-mode interface. J. Fluid Mech. 872, 729–751.CrossRefGoogle Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & NIC Team 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21 (2), 020501.CrossRefGoogle Scholar
Liu, C., Zhang, Y. & Xiao, Z. 2023 A unified theoretical model for spatiotemporal development of Rayleigh–Taylor and Richtmyer–Meshkov fingers. J. Fluid Mech. 954, A13.CrossRefGoogle Scholar
Liu, L., Liang, Y., Ding, J., Liu, N. & Luo, X. 2018 An elaborate experiment on the single-mode Richtmyer–Meshkov instability. J. Fluid Mech. 853, R2.CrossRefGoogle Scholar
Livescu, D. 2013 Numerical simulations of two-fluid turbulent mixing at large density ratios and applications to the Rayleigh–Taylor instability. Phil. Trans. R. Soc. A 371 (2003), 20120185.CrossRefGoogle Scholar
Livescu, D. 2020 Turbulence with large thermal and compositional density variations. Annu. Rev. Fluid Mech. 52, 309–341.CrossRefGoogle Scholar
Livescu, D., Ristorcelli, J.R., Petersen, M.R. & Gore, R.A. 2010 New phenomena in variable-density Rayleigh–Taylor turbulence. Phys. Scr. 2010 (T142), 014015.CrossRefGoogle Scholar
Morgan, R.V., Likhachev, O.A. & Jacobs, J.W. 2016 Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory. J. Fluid Mech. 791, 34–60.CrossRefGoogle Scholar
Müller, B. 2020 Hydrodynamics of core-collapse supernovae and their progenitors. Living Rev. Comput. Astrophys. 6 (1), 3.CrossRefGoogle Scholar
Oron, D., Arazi, L., Kartoon, D., Rikanati, A., Alon, U. & Shvarts, D. 2001 Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 8, 2883–2889.CrossRefGoogle Scholar
Ramaprabhu, P. & Dimonte, G. 2005 Single-mode dynamics of the Rayleigh–Taylor instability at any density ratio. Phys. Rev. E 71 (3), 036314.CrossRefGoogle ScholarPubMed
Ramaprabhu, P., Dimonte, G., Woodward, P., Fryer, C., Rockefeller, G., Muthuraman, K., Lin, P.H. & Jayaraj, J. 2012 The late-time dynamics of the single-mode Rayleigh–Taylor instability. Phys. Fluids 24 (7), 074107.CrossRefGoogle Scholar
Ramaprabhu, P., Dimonte, G., Young, Y.-N., Calder, A.C. & Fryxell, B. 2006 Limits of the potential flow approach to the single-mode Rayleigh–Taylor problem. Phys. Rev. E 74 (6), 066308.CrossRefGoogle Scholar
Ranjan, D., Anderson, M., Oakley, J. & Bonazza, R. 2005 Experimental investigation of a strongly shocked gas bubble. Phys. Rev. Lett. 94, 184507.CrossRefGoogle ScholarPubMed
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock–bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Read, K.I. 1984 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12 (1–3), 45–58.CrossRefGoogle Scholar
Roberts, M.S. & Jacobs, J.W. 2016 The effects of forced small-wavelength, finite-bandwidth initial perturbations and miscibility on the turbulent Rayleigh–Taylor instability. J. Fluid Mech. 787, 50–83.CrossRefGoogle Scholar
Sane, A., Mandre, S. & Kim, I. 2018 Surface tension of flowing soap films. J. Fluid Mech. 841, R2.CrossRefGoogle Scholar
Seiwert, J., Dollet, B. & Cantat, I. 2014 Theoretical study of the generation of soap films: role of interfacial visco-elasticity. J. Fluid Mech. 739, 124–142.CrossRefGoogle Scholar
Sharp, D.H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12 (1), 3–18.CrossRefGoogle Scholar
Snider, D.M. & Andrews, M.J. 1994 Rayleigh–Taylor and shear driven mixing with an unstable thermal stratification. Phys. Fluids 6 (10), 3324–3334.CrossRefGoogle Scholar
Sohn, S.I. 2003 Simple potential-flow model of Rayleigh–Taylor and Richtmyer–Meshkov instabilities for all density ratios. Phys. Rev. E 67, 026301.CrossRefGoogle ScholarPubMed
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Waddell, J.T., Niederhaus, C.E. & Jacobs, J.W. 2001 Experimental study of Rayleigh–Taylor instability: low Atwood number liquid systems with single-mode initial perturbations. Phys. Fluids 13 (5), 1263–1273.CrossRefGoogle Scholar
Wei, T. & Livescu, D. 2012 Late-time quadratic growth in single-mode Rayleigh–Taylor instability. Phys. Rev. E 86 (4), 046405.CrossRefGoogle ScholarPubMed
White, J., Oakley, J., Anderson, M. & Bonazza, R. 2010 Experimental measurements of the nonlinear Rayleigh–Taylor instability using a magnetorheological fluid. Phys. Rev. E 81 (2), 026303.CrossRefGoogle ScholarPubMed
Wilkinson, J.P. & Jacobs, J.W. 2007 Experimental study of the single-mode three-dimensional Rayleigh–Taylor instability. Phys. Fluids 19, 124102.CrossRefGoogle Scholar
Youngs, D.L. 1989 Modelling turbulent mixing by Rayleigh–Taylor instability. Physica D 37 (1–3), 270–287.CrossRefGoogle Scholar
Youngs, D.L. 2013 The density ratio dependence of self-similar Rayleigh–Taylor mixing. Phil. Trans. R. Soc. A 371 (2003), 20120173.CrossRefGoogle ScholarPubMed
Youngs, D.L. & Read, K.I. 1983 Experimental investigation of turbulent mixing by Rayleigh–Taylor instability. Tech. Rep. O11/83. Atomic Weapons Research Establishment Report.Google Scholar
Zhang, J., Childress, S., Libchaber, A. & Shelley, M. 2000 Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind. Nature 408 (6814), 835–839.CrossRefGoogle Scholar
Zhang, Q. 1998 Analytical solutions of Layzer-type approach to unstable interfacial fluid mixing. Phys. Rev. Lett. 81 (16), 3391.CrossRefGoogle Scholar
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.CrossRefGoogle Scholar
Zhou, Y. 2017 a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zhou, Y. 2017 b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723–725, 1–160.Google Scholar
Zhou, Y., Clark, T.T., Clark, D.S., Glendinning, S.S., Skinner, A.A., Huntington, C., Hurricane, O.A., Dimits, A.M. & Remington, B.A. 2019 Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 26 (8), 080901.CrossRefGoogle Scholar