Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T23:57:34.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of solute blobs in heterogeneous porous media

Published online by Cambridge University Press:  29 August 2018

M. Dentz Open the ORCID record for M. Dentz [Opens in a new window] ,
F. P. J. de Barros ,
T. Le Borgne  and
D. R. Lester Open the ORCID record for D. R. Lester [Opens in a new window]
M. Dentz*
Affiliation:
Spanish National Research Council, IDAEA-CSIC, c/Jordi Girona 18, 08034 Barcelona, Spain
F. P. J. de Barros
Affiliation:
Sonny Astani Department of Civil and Environmental Engineering, University of Southern California, Los Angeles, CA 90089, USA
T. Le Borgne
Affiliation:
Geosciences Rennes, UMR 6118, Université de Rennes 1, CNRS, 35042 Rennes, France
D. R. Lester
Affiliation:
School of Civil, Environmental and Chemical Engineering, RMIT University, Melbourne, Victoria 3001, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the mixing dynamics of solute blobs in the flow through saturated heterogeneous porous media. As the solute plume is advected through a heterogeneous porous medium it suffers a series of deformations that determine its mixing with the ambient fluid through diffusion. Key questions are the relation between the spatial disorder and the mixing dynamics and the effect of the initial solute distribution. To address these questions, we formulate the advection–diffusion problem in a coordinate system that moves and rotates along streamlines of the steady flow field. The impact of the medium heterogeneity is quantified systematically within a stochastic modelling approach. 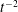For a simple shear flow, the maximum concentration of a blob decays asymptotically as $t^{-2}$. For heterogeneous porous media, the mixing of the solute blob is determined by the random sampling of flow and deformation heterogeneity along trajectories, a mechanism different from persistent shear. We derive explicit perturbation theory expressions for stretching-enhanced solute mixing that relate the medium structure and mixing behaviour. The solution is valid for moderate heterogeneity. The random sampling of shear along trajectories leads to a 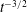$t^{-3/2}$ decay of the maximum concentration as opposed to an equivalent homogeneous medium, for which it decays as 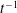$t^{-1}$.

JFM classification

Low-Reynolds-number flows: Porous media Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 621 - 646
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

de Anna, P., Dentz, M., Tartakovsky, A. & Le Borgne, T. 2014 The filamentary structure of mixing fronts and its control on reaction kinetics in porous media flows. Geophys. Res. Lett. 41, 4586–4593.Google Scholar
Aquino, T. & Bolster, D. 2017 Localized point mixing rate potential in heterogeneous velocity fields. Trans. Porous Med. 119 (2), 391–402.Google Scholar
Arnol’d, V. I. 1966 On the topology of three-dimensional steady flows of an ideal fluid. Z. Angew. Math. Mech. J. Appl. Math. Mech. 30, 223–226.Google Scholar
de Barros, F. P. J., Dentz, M., Koch, J. & Nowak, W. 2012 Flow topology and scalar mixing in spatially heterogeneous flow fields. Geophys. Res. Lett. 39 (8), L08404.Google Scholar
de Barros, F. P. J., Fernàndez-Garcia, D., Bolster, D. & Sanchez-Vila, X. 2013 A risk-based probabilistic framework to estimate the endpoint of remediation: concentration rebound by rate-limited mass transfer. Water Resour. Res. 49 (4), 1929–1942.Google Scholar
de Barros, F. P. J., Fiori, A., Boso, F. & Bellin, A. 2015 A theoretical framework for modeling dilution enhancement of non-reactive solutes in heterogeneous porous media. J. Contam. Hydrol. 175, 72–83.Google Scholar
de Barros, F. P. J. & Rubin, Y. 2008 A risk-driven approach for subsurface site characterization. Water Resour. Res. 44 (1), W01414.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5 (1), 113–133.Google Scholar
Battiato, I., Tartakovsky, D. M., Tartakovsky, A. M. & Scheibe, T. 2009 On breakdown of macroscopic models of mixing-controlled heterogeneous reactions in poroous media. Adv. Water Resour. 32, 1664–1673.Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. American Elsevier Publishing Company, Inc.Google Scholar
Bolster, D., Dentz, M. & Le Borgne, T. 2011a Hypermixing in linear shear flow. Water Resour. Res. 47 (9), W09602.Google Scholar
Bolster, D., Valdés-Parada, F. J., LeBorgne, T., Dentz, M. & Carrera, J. 2011b Mixing in confined stratified aquifers. J. Contam. Hydrol. 120, 198–212.Google Scholar
Cushman, J. H., Hu, X. & Ginn, T. R. 1994 Nonequilibrium statistical mechanics of preasymptotic dispersion. J. Stat. Phys. 75 (5–6), 859–878.Google Scholar
Dagan, G. 1987 Theory of solute transport by groundwater. Annu. Rev. Fluid Mech. 19 (1), 183–213.Google Scholar
Dagan, G. 1990 Transport in heterogenous porous formations: spatial moments, ergodicity, and effective dispersion. Water Resour. Res. 26, 1287–1290.Google Scholar
De Simoni, M., Carrera, J., Sánchez-Vila, X. & Guadagnini, A. 2005 A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 41, W11410.Google Scholar
Dentz, M., Kang, P., Comolli, A., Le Borgne, T. & Lester, D. R. 2016a Continuous time random walks for the evolution of Lagrangian velocities. Phys. Rev. Fluids 074004.Google Scholar
Dentz, M., Kinzelbach, H., Attinger, S. & Kinzelbach, W. 2000 Temporal behavior of a solute cloud in a heterogeneous porous medium, 1, point-like injection. Water Resour. Res. 36 (12), 3591–3604.Google Scholar
Dentz, M., Le Borgne, T., Englert, A. & Bijeljic, B. 2011 Mixing, spreading and reaction in heterogeneous media: a brief review. J. Contam. Hydrol. 120, 1–17.Google Scholar
Dentz, M., Lester, D. R., Borgne, T. L. & de Barros, F. P. J. 2016b Coupled continuous time random walks for fluid stretching in two-dimensional heterogeneous media. Phys. Rev. E 061102(R).Google Scholar
Dentz, M., Tartakovsky, D. M., Abarca, E., Guadagnini, A. & Carrera, X. S.-V. J. 2006 Variable-density flow in porous media. J. Fluid Mech. 561, 209–235.Google Scholar
Duplat, J. & Villermaux, E. 2008 Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86.Google Scholar
Engdahl, N. B., Benson, D. A. & Bolster, D. 2014 Predicting the enhancement of mixing-driven reactions in nonuniform flows using measures of flow topology. Phys. Rev. E 90 (5), 051001.Google Scholar
Fiori, A. & Dagan, G. 2000 Concentration fluctuations in aquifer transport: a rigorous first-order solution and applications. J. Contam. Hydrol. 45 (1), 139–163.Google Scholar
Gelhar, L. W. & Axness, C. L. 1983 Three-dimensional stochastic analysis of macrodispersion in aquifers. Water Resour. Res. 19 (1), 161–180.Google Scholar
Henri, C. V., Fernàndez-Garcia, D. & Barros, F. P. J. 2015 Probabilistic human health risk assessment of degradation-related chemical mixtures in heterogeneous aquifers: risk statistics, hot spots, and preferential channels. Water Resour. Res. 51 (6), 4086–4108.Google Scholar
Kapoor, V. & Kitanidis, P. 1998 Concentration fluctuations and dilution in aquifers. Water Resour. Res. 34 (5), 1181–1193.Google Scholar
Kitanidis, P. 1994 The concept of the dilution index. Water Resour. Res. 30 (7), 2011–2026.Google Scholar
Koch, D. L. & Brady, J. F. 1987 A non-local description of advection–diffusion with application to dispersion in porous media. J. Fluid Mech. 180, 387–403.Google Scholar
Lapeyre, G., Klein, P. & Hua, B. L. 1999 Does the tracer gradient vector align with the strain eigenvectors in 2d turbulence? Phys. Fluids 11 (12), 3729–3737.Google Scholar
Le Borgne, T., Dentz, M., Bolster, D., Carrera, J., de Dreuzy, J.-R. & Davy, P. 2010 Non-Fickian mixing: temporal evolution of the scalar dissipation rate in heterogeneous porous media. Adv. Water Resour. 33 (12), 1468–1475.Google Scholar
Le Borgne, T., Dentz, M., Davy, P., Bolster, D., Carrera, J., De Dreuzy, J.-R. & Bour, O. 2011 Persistence of incomplete mixing: a key to anomalous transport. Phys. Rev. E 84 (1), 015301.Google Scholar
Le Borgne, T., Dentz, M. & Villermaux, E. 2013 Stretching, coalescence, and mixing in porous media. Phys. Rev. Lett. 110 (20), 204501.Google Scholar
Le Borgne, T., Dentz, M. & Villermaux, E. 2015 The lamellar description of mixing in porous media. J. Fluid Mech. 770, 458–498.Google Scholar
Le Borgne, T., Ginn, T. R. & Dentz, M. 2014 Impact of fluid deformation on mixing-induced chemical reactions in heterogeneous flows. Geophys. Res. Lett. 41 (22), 7898–7906.Google Scholar
Lester, D., Dentz, M., Le Borgne, T. & de Barros, F. P. J. 2018 Fluid deformation in random steady three dimensional flow. J. Fluid Mech. (in press).Google Scholar
Lester, D. R., Metcalfe, G. & Trefry, M. G. 2013 Is chaotic advection inherent to porous media flow? Phys. Rev. Lett. 111, 174101.Google Scholar
Lester, D. R., Rudman, M., Metcalfe, G., Trefry, M. G., Ord, A. & Hobbs, B. 2010 Scalar dispersion in a periodically reoriented potential flow: acceleration via Lagrangian chaos. Phys. Rev. E 81, 046319.Google Scholar
Matheron, G. 1968 Composition des perméabilités en milieu poreux. Revue de l’Institut Français du Petrole 23 (2), 201–218.Google Scholar
Matheron, M. & de Marsily, G. 1980 Is transport in porous media always diffusive? Water Resour. Res. 16, 901–917.Google Scholar
Meunier, P. & Villermaux, E. 2003 How vortices mix. J. Fluid Mech. 476, 213–222.Google Scholar
Meunier, P. & Villermaux, E. 2010 The diffusive strip method for scalar mixing in two dimensions. J. Fluid Mech. 662, 134–172.Google Scholar
Neuman, S. P. 1993 Eulerian–Lagangian theory of transport in space-time nonstationary velocity fields: exact nonlocal formalism by conditional moments and weak approximation. Water Resour. Res. 29 (3), 633–645.Google Scholar
Okubo, A. 1968 Some remarks on the importance of the shear effect on horizontal diffusion. J. Oceanogr. Soc. Japan 24, 60–69.Google Scholar
Okubo, A. 1970 Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep-Sea Res. 17, 445–454.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport, vol. 3. Cambridge University Press.Google Scholar
Pollock, D. W. 1988 Semianalytical computation of path lines for finite difference models. Ground Water 26 (6), 743–750.Google Scholar
Ranz, W. E. 1979 Application of a stretch model to mixing, diffusion and reaction in laminar and turbulent flows. AIChE J. 25 (1), 41–47.Google Scholar
Risken, H. 1996 The Fokker–Planck Equation. Springer.Google Scholar
Rubin, Y. 2003 Applied Stochastic Hydrology. Oxford University Press.Google Scholar
Steefel, C. I., DePaolo, D. J. & Lichtner, P. C. 2005 Reactive transport modeling: an essential tool and a new research approach for the earth sciences. Earth Planet. Sci. Lett. 240, 539–558.Google Scholar
Tartakovsky, A. M., Tartakovsky, D. M. & Meakin, P. 2008 Stochastic Langevin model for flow and transport in porous media. Phys. Rev. Lett. 101, 044502.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Villermaux, E. 2012 Mixing by porous media. C. R. Méc. 340 (11), 933–943.Google Scholar
Weeks, S. & Sposito, G. 1998 Mixing and stretching efficiency in steady and unsteady groundwater flows. Water Resour. Res. 34 (12), 3315–3322.Google Scholar
Weiss, J. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48 (2), 273–294.Google Scholar
Ye, Y., Chiogna, G., Cirpka, O. A., Grathwohl, P. & Rolle, M. 2015 Experimental evidence of helical flow in porous media. Phys. Rev. Lett. 115, 194502.Google Scholar