Published online by Cambridge University Press: 01 May 2012
We present results from an experimental study of the speed and shape of the ejecta formed when a solid sphere impacts onto a granular bed. We use high-speed imaging at frame rates up to 100 000 f.p.s. to provide direct measurement of individual grain velocities and ejecta angles as well as the overall evolution of the granular ejecta. For larger grain sizes, the emergence velocities of the grains during the ‘early stage flow’, i.e. before the main ejecta ‘curtain’ forms, increase with the kinetic energy of the impacting sphere but are inversely proportional to the time from impact. We also observe that the fastest grains, which can obtain velocities up to five times that of the impacting sphere (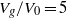 ), generally emerge at the earliest times and with the lowest ejection angles. As the grain size is decreased, a more ‘fluid-like’ behaviour is observed whereby the ejected material first emerges as a thin sheet of grains between the sphere and the bed surface, which is also seen when a sphere impacts a liquid pool. In this case, the sheet velocity is approximately double that of the impacting sphere (
), generally emerge at the earliest times and with the lowest ejection angles. As the grain size is decreased, a more ‘fluid-like’ behaviour is observed whereby the ejected material first emerges as a thin sheet of grains between the sphere and the bed surface, which is also seen when a sphere impacts a liquid pool. In this case, the sheet velocity is approximately double that of the impacting sphere (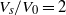 ) and independent of the bulk packing fraction. For the finest grains we provide evidence of the existence of a vortex ring inside the ejecta curtain where grains following the air flow are entrained through the curtain. In contrast to predictions from previous studies, we find that the temporal evolution of the ejecta neck radius is not initially quadratic but rather approaches a square-root dependence on time, for the finest grains with the highest impact kinetic energy. The evolution therefore approaches that seen for the crown evolution in liquid drop impacts. By using both spherical glass beads and coarse sands, we show that the size and shape distribution are critical in determining the post-impact dynamics whereby the sands exhibit a qualitatively different response to impact, with grains ejected at lower speeds and at later times than for the glass beads.
) and independent of the bulk packing fraction. For the finest grains we provide evidence of the existence of a vortex ring inside the ejecta curtain where grains following the air flow are entrained through the curtain. In contrast to predictions from previous studies, we find that the temporal evolution of the ejecta neck radius is not initially quadratic but rather approaches a square-root dependence on time, for the finest grains with the highest impact kinetic energy. The evolution therefore approaches that seen for the crown evolution in liquid drop impacts. By using both spherical glass beads and coarse sands, we show that the size and shape distribution are critical in determining the post-impact dynamics whereby the sands exhibit a qualitatively different response to impact, with grains ejected at lower speeds and at later times than for the glass beads.
Movie 1. Sequences from video clips taken at 12,000 fps. Four different media are shown in this clip. The first 3 are glass beads with diameters 520, 178 and 31 μm and the final panel is water. In each sequence, the impacting sphere has a diameter of 25 mm and velocity of 9.8m/s prior to impact.
Movie 2. Video clip taken at 100,000 fps showing the emergence of a fluid-like granular sheet for fine grains. The sphere diameter is 50 mm, the impact velocity is 2.6 m/s and the grains are 31 μm.
Movie 3. Video clip taken at 1000,000 fps showing the high-speed ejecta generated during the impact of a 50 mm sphere onto a pool of water. The impact velocity was 9.45 m/s.