Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T05:49:47.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Euler and Navier–Stokes equations in a new time-dependent helically symmetric system: derivation of the fundamental system and new conservation laws

Published online by Cambridge University Press:  31 March 2017

Dominik Dierkes Open the ORCID record for Dominik Dierkes [Opens in a new window]  and
Martin Oberlack
Dominik Dierkes*
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Str. 2, 64287 Darmstadt, Germany Graduate School of Excellence Computational Engineering, TU Darmstadt, Dolivostr. 15, 64293 Darmstadt, Germany
Martin Oberlack
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Str. 2, 64287 Darmstadt, Germany Graduate School of Excellence Computational Engineering, TU Darmstadt, Dolivostr. 15, 64293 Darmstadt, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present contribution is a significant extension of the work by Kelbin et al. (J. Fluid Mech., vol. 721, 2013, pp. 340–366) as a new time-dependent helical coordinate system has been introduced. For this, Lie symmetry methods have been employed such that the spatial dependence of the originally three independent variables is reduced by one and the remaining variables are: the cylindrical radius $r$ and the time-dependent helical variable 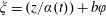$\unicode[STIX]{x1D709}=(z/\unicode[STIX]{x1D6FC}(t))+b\unicode[STIX]{x1D711}$, 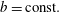$b=\text{const.}$ and time $t$. The variables $z$ and 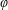$\unicode[STIX]{x1D711}$ are the usual cylindrical coordinates and 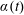$\unicode[STIX]{x1D6FC}(t)$ is an arbitrary function of time $t$. Assuming 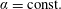$\unicode[STIX]{x1D6FC}=\text{const.}$, we retain the classical helically symmetric case. Using this, and imposing helical invariance onto the equation of motion, leads to a helically symmetric system of Euler and Navier–Stokes equations with a time-dependent pitch 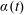$\unicode[STIX]{x1D6FC}(t)$, which may be varied arbitrarily and which is explicitly contained in all of the latter equations. This has been conducted both for primitive variables as well as for the vorticity formulation. Hence a significantly extended set of helically invariant flows may be considered, which may be altered by an external time-dependent strain along the axis of the helix. Finally, we sought new conservation laws which can be found from the helically invariant Euler and Navier–Stokes equations derived herein. Most of these new conservation laws are considerable extensions of existing conservation laws for helical flows at a constant pitch. Interestingly enough, certain classical conservation laws do not admit extensions in the new time-dependent coordinate system.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 344 - 365
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anco, S. C. & Bluman, G. W. 2002a Direct construction method for conservation laws of partial differential equations part ii: General treatment. Eur. J. Appl. Maths 13 (05), 567–585.CrossRefGoogle Scholar
Anco, S. C. & Bluman, G. W. 2002b Symmetry and Integration Methods for Differential Equations. Springer.Google Scholar
Bluman, G. W., Cheviakov, A. F. & Anco, S. C. 2010 Applications of Symmetry Methods to Partial Differential Equations. Springer.CrossRefGoogle Scholar
Bogoyavlenskij, O. I. 2000 Helically symmetric astrophysical jets. Phys. Rev. E 62, 8616–8627.Google ScholarPubMed
Cheviakov, A. F. 2007 Gem software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 176 (1), 48–61.CrossRefGoogle Scholar
Cheviakov, A. F. & Oberlack, M. 2014 Generalized Ertel’s theorem and infinite hierarchies of conserved quantities for three-dimensional time-dependent Euler and Navier–Stokes equations. J. Fluid Mech. 760, 368–386.CrossRefGoogle Scholar
Delbende, I., Rossi, M. & Daube, O. 2012 DNS of flows with helical symmetry. Theor. Comput. Fluid Dyn. 26 (1–4), 141–160.CrossRefGoogle Scholar
Dritschel, D. G. 1991 Generalized helical Beltrami flows in hydrodynamics and magnetohydrodynamics. J. Fluid Mech. 222, 525–541.CrossRefGoogle Scholar
Jamil, M. & Fetecau, C. 2010 Helical flows of Maxwell fluid between coaxial cylinders with given shear stresses on the boundary. Nonlinear Anal. Real World Appl. 11 (5), 4302–4311.CrossRefGoogle Scholar
Johnson, J. L., Oberman, C. R., Kulsrud, R. M. & Frieman, E. A.1958 Some stable hydromagnetic equilibria. 1 (4), 281–296.Google Scholar
Kelbin, O., Cheviakov, A. F. & Oberlack, M. 2013 New conservation laws of helically symmetric, plane and rotationally symmetric viscous and inviscid flows. J. Fluid Mech. 721, 340–366.CrossRefGoogle Scholar
Mitchell, A., Morton, S. & Forsythe, J.1997 Wind turbine wake aerodynamics Rep. ADA425027. Air Force Academy Colorado Springs, Department of Aeronautics.Google Scholar
Oberlack, M. 2000 Symmetrie, Invarianz und Selbstähnlichkeit in der Turbulenz. Shaker Aachen.Google Scholar
Rosenhaus, V. & Shankar, R.2015 Sub-symmetries and infinite conservation laws for the Euler equations. arXiv:1509.05101.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (03), 545–559.CrossRefGoogle Scholar
Schnack, D. D., Caramana, E. J. & Nebel, R. A. 1985 Three-dimensional magnetohydrodynamic studies of the reversed-field pinch. Phys. Fluids 28 (1), 321–333.CrossRefGoogle Scholar
Vermeer, L. J., Sorensen, J. N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39 (6–7), 467–510.CrossRefGoogle Scholar
Zienkiewicz, O. C., Taylor, R. L., Sherwin, S. J. & Peiro, J. 2003 On discontinuous Galerkin methods. Int. J. Numer. Meth. Engng 58 (8), 1119–1148.CrossRefGoogle Scholar