Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-10T05:59:17.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Energetic scales in a bluff body shear layer

Published online by Cambridge University Press:  22 July 2019

D. M. Moore ,
C. W. Letchford  and
M. Amitay Open the ORCID record for M. Amitay [Opens in a new window]
D. M. Moore
Affiliation:
Center for Flow Physics and Control, Department of Mechanical Aeronautical and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
C. W. Letchford
Affiliation:
Department of Civil and Environmental Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
M. Amitay*
Affiliation:
Center for Flow Physics and Control, Department of Mechanical Aeronautical and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

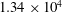A detailed experimental campaign into separated shear layers stemming from rectangular sections (having aspect ratios of 5 : 1, 3 : 1 and 1 : 1) was carried out at Reynolds numbers range between $1.34\times 10^{4}$ and 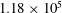$1.18\times 10^{5}$ based on the body thickness. Particle image velocimetry was used to locate the highest concentration of fluctuations in the velocity field and subsequent hot-wire measurements at those locations provided adequate spectral resolution to follow the evolution of various instabilities that are active within the separated shear layer. Similar to recent findings by this same group, the shear layer behaviour is observed to contain a combination of Reynolds invariant characteristics, including its time-averaged position, while other properties demonstrate clear Reynolds number dependency, including the spatial amplification of turbulent kinetic energy. Additional results here show that the ratio of side lengths of the body is a key parameter in revealing these effects. One reason for this is the level of coupling between modes of instability, which is evaluated using two-point correlation methods. These findings indicate that the separated shear layer on a bluff body is highly nonlinear. A specific set of scales responsible for these unique behaviours is identified and discussed, along with their relationship to other scales in the flow.

JFM classification

Wakes/Jets: Shear layers Instability: Transition to turbulence Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 875 , 25 September 2019 , pp. 543 - 575
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1971 Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 46 (2), 321–335.10.1017/S0022112071000569Google Scholar
Akon, A. F. & Kopp, G. A. 2018 Turbulence structure and similarity in the separated flow above a low building in the atmospheric boundary layer. J. Wind Engng Ind. Aerodyn. 182 (April), 87–100.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.10.1063/1.864901Google Scholar
Bartoli, G., Bruno, L., Buresti, G., Ricciardelli, F., Salvetti, M. V. & Zasso, A.2008 BARC overview document. Available at: http://www.aniv-iawe.org/barc.Google Scholar
Bearman, P. W. & Morel, T. 1983 Effect of free stream turbulence on the flow around bluff bodies. Prog. Aerosp. Sci. 20 (2–3), 97–123.10.1016/0376-0421(83)90002-7Google Scholar
Bloor, S. M. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19 (02), 290–304.Google Scholar
Brown, G. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Bruno, L., Fransos, D., Coste, N. & Bosco, A. 2010 3D flow around a rectangular cylinder: a computational study. J. Wind Engng Ind. Aerodyn. 98, 263–276.10.1016/j.jweia.2009.10.005Google Scholar
Bruno, L., Salvetti, M. V. & Ricciardelli, F. 2014 Benchmark on the aerodynamics of a rectangular 5 : 1 cylinder: an overview after the first four years of activity. J. Wind Engng Ind. Aerodyn. 126, 87–106.10.1016/j.jweia.2014.01.005Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.10.1017/S0022112083002189Google Scholar
Carter, D. W. & Coletti, F. 2018 Small-scale structure and energy transfer in homogeneous turbulence. J. Fluid Mech. 854, 505–543.10.1017/jfm.2018.616Google Scholar
Castro, I. P. & Haque, A. 1987 The structure of a turbulent shear layer bounding a separation region. J. Fluid Mech. 179, 439–468.10.1017/S0022112087001605Google Scholar
Christensen, K. T. & Scarano, F. 2015 Uncertainty quantification in particle image velocimetry. Meas. Sci. Technol. 26 (7), 6–8.10.1088/0957-0233/26/7/070201Google Scholar
Fiedler, E. 1991 The spatially accelerated mixing layer in a tailored pressure gradient. Eur. J. Mech. (B/Fluids) 10 (4), 349–376.Google Scholar
Ho, C. M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–424.10.1146/annurev.fl.16.010184.002053Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.10.1146/annurev.fl.22.010190.002353Google Scholar
Hultgren, L. S. & Aggarwal, A. K. 1987 Absolute instability of the Gaussian wake profile. Phys. Fluids 30 (11), 3383–3388.10.1063/1.866470Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Lander, D. C.2017 Influence of freestream and forced disturbances on the shear layers of a square prism. PhD thesis, Rensselaer Polytechnic Institute.Google Scholar
Lander, D. C., Moore, D. M., Letchford, C. W. & Amitay, M. 2018 Scaling of square-prism shear layers. J. Fluid Mech. 849, 1096–1119.10.1017/jfm.2018.443Google Scholar
Mannini, C., Šoda, A. & Schewe, G. 2010 Computers & fluids unsteady RANS modelling of flow past a rectangular cylinder: investigation of Reynolds number effects. Comput. Fluids 39 (9), 1609–1624.10.1016/j.compfluid.2010.05.014Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946Google Scholar
Matsumoto, M. 1999 Vortex shedding of bluff bodies: a review. J. Fluids Struct. 13 (7-8), 791–811.10.1006/jfls.1999.0249Google Scholar
Melbourne, W. H. 1979 Turbulence effects on maximum surface pressures – a mechanism and possibility of reduction. In Fifth International Conference on Wind Engineering, pp. 541–551. Pergamon Press.Google Scholar
Michalke, A. 1965 On spatially growing disturbance in an inviscid shear layer. J. Fluid Mech. 23, 521–544.10.1017/S0022112065001520Google Scholar
Monkewitz, P. A. 1982 Influence of the velocity ratio on the spatial instability of mixing layers. Phys. Fluids 25 (7), 1137–1143.Google Scholar
Morrison, M. J. & Kopp, G. A. 2018 Effects of turbulence intensity and scale on surface pressure fluctuations on the roof of a low-rise building in the atmospheric boundary layer. J. Wind Engng Ind. Aerodyn. 183 (June), 140–151.Google Scholar
Morton, B. R. 1984 The generation and decay of vorticity. Geophys. Astrophys. Fluid Dyn. 28 (3–4), 277–308.10.1080/03091928408230368Google Scholar
Neal, D. R., Sciacchitano, A., Smith, B. L. & Scarano, F. 2015 Collaborative framework for PIV uncertainty quantification: the experimental database. Meas. Sci. Technol. 26 (7), 1–17.10.1088/0957-0233/26/7/074003Google Scholar
Norberg, C. 1993 Flow around rectangular cylinders: pressure forces and wake frequencies. J. Wind Engng Ind. Aerodyn. 49, 187–196.10.1016/0167-6105(93)90014-FGoogle Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.Google Scholar
Prosser, D. T. & Smith, M. J. 2016 Numerical characterization of three-dimensional bluff body shear layer behaviour. J. Fluid Mech. 799, 1–26.10.1017/jfm.2016.344Google Scholar
Roshko, A.1954 On the drag and shedding frequency of two-dimensional bluff bodies. Tech. Rep. National Advisory Committee for Aeronautics, Washington.Google Scholar
Sato, H. 1956 Experimental investigation on the transition of laminar separated layer. J. Phys. Soc. Japan 11 (6), 702–709.10.1143/JPSJ.11.702Google Scholar
Schewe, G. 2013 Reynolds-number-effects in flow around a rectangular cylinder with aspect ratio 1 : 5. J. Fluids Struct. 39, 15–26.10.1016/j.jfluidstructs.2013.02.013Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.10.1007/978-1-4613-0185-1Google Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 1–16.10.1088/0957-0233/27/8/084006Google Scholar
Shimada, K. & Ishihara, T. 2002 Application of a modified k–e model to the prediction of aerodynamic characteristics of rectangular cross-section cylinders. J. Fluids Struct. 16 (15), 399–413.10.1006/jfls.2001.0433Google Scholar
Sigurdson, L. W.1986 The structure and control of a turbulent reattaching flow. PhD thesis, California Institute of Technology.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Tieleman, H. W. 2003 Wind tunnel simulation of wind loading on low-rise structures: a review. J. Wind Engng Ind. Aerodyn. 91 (12–15), 1627–1649.10.1016/j.jweia.2003.09.021Google Scholar
Trias, F. X., Gorobets, A. & Oliva, A. 2015 Turbulent flow around a square cylinder at Reynolds number 22 000: a DNS study. Comput. Fluids 123 (22), 87–98.10.1016/j.compfluid.2015.09.013Google Scholar
Unal, M. F. & Rockwell, D. 1988 On vortex formation from a cylinder. Part 1. The initial instability. J. Fluid Mech. 190, 491–512.10.1017/S0022112088001429Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (02), 237–255.10.1017/S0022112074001121Google Scholar