Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-10T05:03:07.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of drop impact onto a solid sphere: spreading and retraction

Published online by Cambridge University Press:  10 July 2017

Yang Zhu ,
Hao-Ran Liu ,
Kai Mu ,
Peng Gao ,
Hang Ding Open the ORCID record for Hang Ding [Opens in a new window]  and
Xi-Yun Lu Open the ORCID record for Xi-Yun Lu [Opens in a new window]
Yang Zhu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Hao-Ran Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Kai Mu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Peng Gao
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Hang Ding*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Xi-Yun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

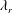In this paper, drop impact onto a sphere is numerically investigated at moderate Reynolds and Weber numbers. It is naturally expected that the aspect ratio of the sphere to the drop, $\unicode[STIX]{x1D706}_{r}$, would make a big difference to drop spreading and retraction on the sphere, compared with drop impact onto a flat substrate. To quantitatively assess the effect of 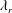$\unicode[STIX]{x1D706}_{r}$, a diffuse-interface immersed-boundary method is adopted after being validated against experiments. With the help of numerical simulations, we identify the key regimes in the spreading and retraction, analyse the results by scaling laws, and quantitatively evaluate the effect of 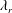$\unicode[STIX]{x1D706}_{r}$ on the impact dynamics. We find that the thickness of the liquid film spreading on the sphere can be well approximated by 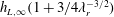$h_{L,\infty }(1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})$, where 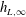$h_{L,\infty }$ represents the film thickness of drop impact on a flat substrate. At the early stage of spreading, the temporal variation of the wetted area is independent of 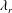$\unicode[STIX]{x1D706}_{r}$ when the time is rescaled by the thickness of the liquid film. Drops are observed to retract on the sphere at a roughly constant speed, and the predictions of theoretical analysis are in good agreement with numerical results.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops Interfacial Flows (free surface): Thin films
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , R3
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bakshi, S., Roisman, I. V. & Tropea, C. 2007 Investigations on the impact of a drop onto a small spherical target. Phys. Fluids 19, 032102.Google Scholar
Bartolo, D., Josserand, C. & Bonn, D. 2005 Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J. Fluid Mech. 545, 329–338.Google Scholar
Biance, A. L., Clanet, C. & Quere, D. 2004 First steps in the spreading of a liquid droplet. Phys. Rev. E 69, 016301.Google Scholar
Clanet, C., BÉGuin, C. & Richard, D. 2004 Maximal deformation of an impacting drop. J. Fluid Mech. 517, 199–208.CrossRefGoogle Scholar
Derby, B. 2010 Inkjet printing of functional and structural materials: fluid property requirements, feature stability, and resolution. Annu. Rev. Mater. Res. 40, 395–414.Google Scholar
Ding, H., Chen, B. Q., Liu, H. R., Zhang, C. Y., Gao, P. & Lu, X. Y. 2015 On the contact-line pinning in cavity formation during solid–liquid impact. J. Fluid Mech. 783, 504–525.Google Scholar
Dressaire, E., Sauret, A. & Boulogne, F. 2016 Drop impact on a flexible fiber. Soft Matt. 12, 200–208.CrossRefGoogle ScholarPubMed
Fedorchenko, A. I. & Wang, A. B. 2004 The formation and dynamics of a blob on free and wall sheets induced by a drop impact on surfaces. Phys. Fluids 16, 3911–3920.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Kim, H. Y., Feng, Z. C. & Chun, J. H. 2000 Instability of a liquid jet emerging from a droplet upon collision with a solid surface. Phys. Fluids 12, 531–541.Google Scholar
Lee, H. G. & Kim, J. 2011 Accurate contact angle boundary conditions for the Cahn–Hilliard equations. Comput. Fluids 44, 178–186.Google Scholar
Liu, H. R. & Ding, H. 2015 A diffuse-interface immersed-boundary method for two-dimensional simulation of flows with moving contact lines on curved substrates. J. Comput. Phys. 294, 484–502.Google Scholar
Liu, Y. H., Andrew, M., Li, J., Yeomans, J. M. & Wang, Z. K. 2015 Symmetry breaking in drop bouncing on curved surfaces. Nat. Commun. 6, 10034.Google Scholar
Liu, Y. H., Moevius, L., Xu, X. P., Qian, T., Yeomans, J. M. & Wang, Z. K. 2014 Pancake bouncing on superhydrophobic surfaces. Nat. Phys. 10, 515–519.Google Scholar
Mitra, S., Nguyen, T. B. T., Doroodchi, E., Pareek, V., Joshi, J. B. & Evans, G. M. 2016 On wetting characteristics of droplet on a spherical particle in film boiling regime. Chem. Engng Sci. 149, 181–203.Google Scholar
Mitra, S., Sathe, M. J. & Doroodchi, E. 2013 Droplet impact dynamics on a spherical particle. Chem. Engng Sci. 100, 105–119.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Rozhkov, A., Prunet-Foch, B. & Vignes-Adler, M. 2002 Impact of water drops on small targets. Phys. Fluids 14, 3485–3501.Google Scholar
Rukosuyev, M. V., Barannyk, O. & Oshkai, P. 2016 Design and application of nanoparticle coating system with decoupled spray generation and deposition control. J. Coat Technol. Res. 13, 769–779.Google Scholar
Stevens, C. S. 2014 Scaling of the splash threshold for low-viscosity fluids. Eur. Phys. Lett. 106, 24001.Google Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing…. Annu. Rev. Fluid Mech. 38, 159–192.CrossRefGoogle Scholar
Zhou, Z. F., Chen, B. & Wang, R. 2017 Comparative investigation on the spray characteristics and heat transfer dynamics of pulsed spray cooling with volatile cryogens. Exp. Therm. Fluid Sci. 82, 189–197.Google Scholar