Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T10:39:54.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical variability of axisymmetric buoyant plumes

Published online by Cambridge University Press:  26 January 2015

A. Ezzamel ,
P. Salizzoni  and
G. R. Hunt
A. Ezzamel
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, Imperial College Road, London SW7 2AZ, UK Laboratoire de Mécanique des Fluides et d’Acoustique, University of Lyon, CNRS UMR 5509 Ecole Centrale de Lyon, INSA Lyon, Université Claude Bernard, 36, avenue Guy de Collongue, 69134 Ecully, France
P. Salizzoni*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, University of Lyon, CNRS UMR 5509 Ecole Centrale de Lyon, INSA Lyon, Université Claude Bernard, 36, avenue Guy de Collongue, 69134 Ecully, France
G. R. Hunt
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental measurements conducted on freely propagating, turbulent, steady thermal air plumes. Three plumes are studied with differing source conditions, ranging from jet-like, momentum flux dominated releases, to pure plume releases, characterised by a balance between the momentum, volume and buoyancy fluxes at the source. Velocity measurements from near the source to a height of tens of source diameters were made using particle image velocimetry (PIV), providing a high spatial resolution. Temperatures were measured with thermocouples. From these measurements, we investigate the vertical development of the plume fluxes and radial profiles of the mean velocity and temperature. 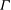These allow us to analyse the local self-preserving characteristics of the mean flow and to estimate the dependence with height of the plume Richardson number ${\it\Gamma}$. In addition, we analyse the similarity of one-point and two-point second-order velocity statistics, and we discuss the role of 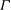${\it\Gamma}$ on the vertical development of the bulk dynamical parameters of the plume, namely, the turbulent viscosity, the turbulent Prandtl number and the entrainment coefficient 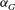${\it\alpha}_{G}$. Comparison with previous experimental results and with estimates of the entrainment coefficient based on the mean kinetic energy budget allow us to conclude on the influence of 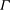${\it\Gamma}$ on the entrainment process and to explain possible physical reasons for the high scatter in estimates of 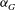${\it\alpha}_{G}$ in the literature.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 576 - 611
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D., Turner, J. S. & Campbell, I. H. 1990 Turbulent fountains in an open chamber. J. Fluid Mech. 212, 557–592.Google Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80, 339–358.CrossRefGoogle Scholar
Burridge, H. C. & Hunt, G. R. 2012 The rise heights of low-and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.Google Scholar
Campbell, A. N. & Cardoso, S. S. S. 2010 Turbulent plumes with internal generation of buoyancy by chemical reaction. J. Fluid Mech. 655, 122–151.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2008 On the dynamics of volcanic columns: a comparison of field data with a new model of negatively buoyant jets. J. Volcanol. Geotherm. Res. 178, 94–103.Google Scholar
Carlotti, P. & Hunt, G. R. 2005 Analytical solutions for turbulent non-Boussinesq plumes. J. Fluid Mech. 538, 343–359.Google Scholar
Caulfield, C. P. & Woods, A. W. 1998 Turbulent gravitational convection from a point source in a non-uniformly stratified environment. J. Fluid Mech. 360, 229–248.Google Scholar
Craske, J. & van Reeuwijk, M.2014 Energy dispersion in turbulent jets. Part 1: direct simulation of steady and unsteady jets. J. Fluid Mech. accepted for publication.Google Scholar
Devenish, B. J., Rooney, G. G. & Thomson, D. J. 2010 Large-eddy simulation of a buoyant plume in uniform and stably stratified environments. J. Fluid Mech. 652, 75–103.Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial condition and coherent structures. In Recent Advances in Turbulence (ed. Arndt, R. E. A. & George, W. K.). Springer.Google Scholar
George, W. K., Alpert, R. & Tamanini, F. 1977 Turbulence measurements in an axisymmetric buoyant plume. Intl J. Heat Mass Transfer 20 (11), 1145–1154.Google Scholar
Hunt, G. R. & Kaye, N. B. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Hunt, G. R. & van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Maths 76 (3), 424–448.Google Scholar
Hussein, J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258 (1), 31–75.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: a review of recent work. Atmos.-Ocean 46 (4), 433–441.CrossRefGoogle Scholar
Kaye, N. B. & Scase, M. M. 2011 Straight-sided solutions to classical and modified plume equations. J. Fluid Mech. 680, 564–573.Google Scholar
Linden, P. F. 2000 Convection in the environment. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G.), pp. 289–345. Cambridge University Press.Google Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14, 189–212.Google Scholar
Mehaddi, R., Vauquelin, O. & Candelier, F. 2012 Analytical solutions for turbulent Boussinesq fountains in a linearly stratified environment. J. Fluid Mech. 691, 487–497.Google Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5, 151–163.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nakagome, H. & Hirata, M.1977 The structure of turbulent diffusion in an axisymmetric turbulent plume. In Proceedings 1976 ICHMT Seminar on Turbulent Buoyant Convection, pp. 361–372. Hemisphere.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 2. Helium jet. J. Fluid Mech. 246 (-1), 225–247.Google Scholar
Papanicolaou, P. N. & List, E. J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195, 341–391.CrossRefGoogle Scholar
Pham, M. V., Plourde, F. & Kim, S. D. 2005 Three-dimensional characterization of a pure thermal plume. Trans. ASME J. Heat Transfer 127, 624–636.Google Scholar
Priestley, C. H. B. & Ball, F. K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81 (348), 144–157.CrossRefGoogle Scholar
Ricou, F. P. & Spalding, D. B. 1961 Measurements of entrainment by axisymmetrical turbulent jets. J. Fluid Mech. 11, 21–32.Google Scholar
Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratfied environment. J. Fluid Mech. 318, 237–250.Google Scholar
Scase, M. M., Caulfield, C. P., Dalziel, S. B. & Hunt, J. C. R. 2006 Time dependent plumes and jets with decreasing source strength. J. Fluid Mech. 563, 443–461.Google Scholar
Shabbir, A. & George, W. K. 1994 Experiments in a round turbulent buoyant plume. J. Fluid Mech. 275, 1–32.CrossRefGoogle Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Ülpre, H., Eames, I. & Greig, A. 2013 Turbulent acidic jets and plumes injected into an alkaline environment. J. Fluid Mech. 743, 253–274.Google Scholar
van den Bremer, T. S. & Hunt, G. R. 2010 Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 644, 165–192.Google Scholar
Wang, H. & Law, A. W.-K. 2002 Second-order integral model for round turbulent jet. J. Fluid Mech. 459, 397–428.Google Scholar
Woods, A. W. 1997 A note on non-Boussinesq plumes in an incompressible stratified environment. J. Fluid Mech. 345, 347–356.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42 (1), 391–412.Google Scholar
Wygnanski, I. & Fiedler, H. E. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38, 577–612.Google Scholar
Zel’dovich, Y. B. 1937 The asymptotic laws of freely-ascending convective flows. Zh. Eksp. Teor. Fiz. 7, 1463–1465.Google Scholar
Zhou, X. 2001 Large-eddy simulation of a turbulent forced plume. Eur. J. Mech. (B/Fluids) 20 (2), 233–254.Google Scholar
Zhou, X. 2002 Vortex dynamics in spatio-temporal development of reacting plumes. Combust. Flame 129 (1–2), 11–29.Google Scholar