Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T19:38:16.507Z Has data issue: false hasContentIssue false
  • English
  • Français

The double backward-facing step: interaction of multiple separated flow regions

Published online by Cambridge University Press:  15 February 2022

Thomas McQueen Open the ORCID record for Thomas McQueen [Opens in a new window] ,
David Burton Open the ORCID record for David Burton [Opens in a new window] ,
John Sheridan Open the ORCID record for John Sheridan [Opens in a new window]  and
Mark C. Thompson Open the ORCID record for Mark C. Thompson [Opens in a new window]
Thomas McQueen*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
David Burton
Affiliation:
Monash Wind Tunnel Research Platform (MWTRP), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

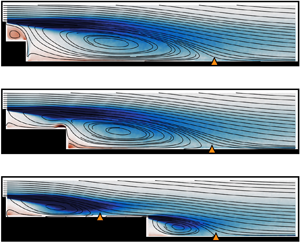
The backward-facing step is perhaps the quintessential geometry used to study separated flow. Extensive previous research has quantified its detailed flow characteristics. However, often regions of separated flow do not exist in isolation; rather, interaction occurs between multiple regions. This motivated an experimental investigation into the time-averaged and dynamic flow features of a double backward-facing step, covering separations of zero to eight step heights between equal-height steps. Three flow regimes are identified. A single reattachment regime occurs for separations of less than four step heights, perhaps remarkable for the lack of variation in key flow characteristics from a single backward-facing step response. Next, an intermediate regime is identified for a separation of four step heights. In this case, the flow does not yet reattach on the first step, although significant differences in reattachment length, surface pressure on the vertical step faces and turbulence statistics occur. Finally, for greater step separations, a double reattachment regime, with reattachment on both steps, is identified. Downwash, induced by the first recirculation zone, reduces the reattachment length and turbulent fluctuations of the second recirculation zone. The surface pressure on the first-step vertical face is reduced, seemingly a result of an upstream influence due to the low pressure in the second-step recirculation zone. Detailed characterisation of the regimes offers insight into the fundamental interaction of regions of separated flow, revealing aspects of complex dynamics relevant to a broad range of practical scenarios.

JFM classification

Wakes/Jets: Separated flows Wakes/Jets: Shear layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 936 , 10 April 2022 , A29
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, E.W. & Johnston, J.P. 1988 a Effects of the separating shear layer on the reattachment flow structure. Part 1. Pressure and turbulence quantities. Exp. Fluids 6 (6), 400–408.CrossRefGoogle Scholar
Adams, E.W. & Johnston, J.P. 1988 b Effects of the separating shear layer on the reattachment flow structure. Part 2. Reattachment length and wall shear stress. Exp. Fluids 6 (7), 493–499.CrossRefGoogle Scholar
Al-Garni, A.M. & Bernal, L.P. 2010 Experimental study of a pickup truck near wake. J. Wind Engng Ind. Aerodyn. 98 (2), 100–112.CrossRefGoogle Scholar
Baker, S. 1977 Regions of recirculating flow associated with two-dimensional steps. Doctoral thesis, University of Surrey.Google Scholar
Bergh, H. & Tijdeman, H. 1965 Theoretical and experimental results for the dynamic response of pressure measuring systems. Nationaal lucht- en ruimtevaartlaboratorium.Google Scholar
Bradshaw, P. & Wong, F.Y.F. 1972 The reattachment and relaxation of a turbulent shear layer. J. Fluid Mech. 52 (1), 113–135.CrossRefGoogle Scholar
Castro, I.P. & Robins, A.G. 1977 The flow around a surface-mounted cube in uniform and turbulent streams. J. Fluid Mech. 79 (2), 307–335.CrossRefGoogle Scholar
Chandrsuda, C. & Bradshaw, P. 1981 Turbulence structure of a reattaching mixing layer. J. Fluid Mech. 110, 171–194.CrossRefGoogle Scholar
Chapman, D.R. 1958 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition. NACA Tech. Rep. NACA-TR-1356.Google Scholar
De Brederode, V. 1975 Three-dimensional effects in nominally two-dimensional flows. PhD thesis, Imperial College London.Google Scholar
Deng, F., Han, G., Liu, M., Ding, J., Weng, P. & Jiang, Z. 2019 Numerical simulation of the interaction of two shear layers in double backward-facing steps. Phys. Fluids 31 (5), 056106.Google Scholar
Driver, D.M. & Seegmiller, H.L. 1985 Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 23 (2), 163–171.CrossRefGoogle Scholar
Fouras, A., Lo Jacono, D. & Hourigan, K. 2008 Target-free stereo PIV: a novel technique with inherent error estimation and improved accuracy. Exp. Fluids 44 (2), 317–329.CrossRefGoogle Scholar
Hart, D.P. 2000 Piv error correction. Exp. Fluids 29 (1), 13–22.CrossRefGoogle Scholar
Hasan, M.A.Z. 1992 The flow over a backward-facing step under controlled perturbation: laminar separation. J. Fluid Mech. 238, 73–96.CrossRefGoogle Scholar
Herry, B.B., Keirsbulck, L., Labraga, L. & Paquet, J.B. 2011 Flow bistability downstream of three-dimensional double backward facing steps at zero-degree sideslip. J. Fluids Engng 133 (5), 054501.CrossRefGoogle Scholar
Kim, J., Kline, S.J. & Johnston, J.P. 1980 Investigation of a reattaching turbulent shear layer: flow over a backward-facing step. J. Fluids Engng 102 (3), 302–308.CrossRefGoogle Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.CrossRefGoogle Scholar
Ma, X. & Schröder, A. 2017 Analysis of flapping motion of reattaching shear layer behind a two-dimensional backward-facing step. Phys. Fluids 29 (11), 115104.CrossRefGoogle Scholar
McQueen, T., Burton, D., Sheridan, J. & Thompson, M.C. 2022 Active control of flow over a backward-facing step at high Reynolds numbers. Intl J. Heat Fluid Flow 93, 108891.CrossRefGoogle Scholar
Miau, J.J., Lee, K.C., Chen, M.H. & Chou, J.H. 1991 Control of separated flow by a two-dimensional oscillating fence. AIAA J. 29 (7), 1140–1148.CrossRefGoogle Scholar
Nadge, P.M. & Govardhan, R.N. 2014 High Reynolds number flow over a backward-facing step: structure of the mean separation bubble. Exp. Fluids 55 (1), 1657.CrossRefGoogle Scholar
Nash, J.F. 1963 An analysis of two-dimensional turbulent base flow, including the effect of the approaching boundary layer. Tech. Rep. ARC R&M 3344. Aeronautical Research Council (Great Britain).Google Scholar
Pawar, S.A., Seshadri, A., Unni, V.R. & Sujith, R.I. 2017 Thermoacoustic instability as mutual synchronization between the acoustic field of the confinement and turbulent reactive flow. J. Fluid Mech. 827, 664–693.CrossRefGoogle Scholar
Rao, A.N., Zhang, J.., Minelli, G., Basara, B. & Krajnović, S. 2019 Qualitative assessment of the bi-stable states in the wake of a finite-width double backward facing step. J. Wind Engng Ind. Aerodyn. 186, 241–249.CrossRefGoogle Scholar
Roshko, A. & Lau, J. 1965 Some observations on transition and reattachment of a free shear layer in incompressible flow. In Proc. Heat Transfer and Fluid Mechanics Institute (Charwat, A. F. ed.), pp. 157–167.Google Scholar
Sciacchitano, A & Wieneke, B 2016 Piv uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.CrossRefGoogle Scholar
Smith, S.M., Venning, J.A., Pearce, B.W., Young, Y.L. & Brandner, P.A. 2020 The influence of fluid–structure interaction on cloud cavitation about a stiff hydrofoil. Part 1. J. Fluid Mech. 896, A1.CrossRefGoogle Scholar
Syms, G.F. 2008 Simulation of simplified-frigate airwakes using a Lattice-Boltzmann method. J. Wind Engng Ind. Aerodyn. 96 (6), 1197–1206.CrossRefGoogle Scholar
Tinney, C.E. & Ukeiley, L.S. 2009 A study of a 3-D double backward-facing step. Exp. Fluids 47 (3), 427–438.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Wang, S., Burton, D., Sheridan, J. & Thompson, M.C. 2014 Characteristics of flow over a double backward-facing step. In Proceedings of the 19th Australasian Fluid Mechanics Conference, AFMC 2014.Google Scholar
Wee, D., Yi, T., Annaswamy, A. & Ghoniem, A.F. 2004 Self-sustained oscillations and vortex shedding in backward-facing step flows: simulation and linear instability analysis. Phys. Fluids 16 (9), 3361–3373.CrossRefGoogle Scholar
Welch, P. 1967 The use of fast fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.CrossRefGoogle Scholar
Wu, Y., Ren, H. & Tang, H. 2013 Turbulent flow over a rough backward-facing step. Intl J. Heat Fluid Flow 44, 155–169.CrossRefGoogle Scholar
Zhang, J., Minelli, G., Basara, B., Bensow, R.. & Krajnović, S. 2021 Yaw effect on bi-stable air-wakes of a generic ship using large eddy simulation. Ocean Engng 219, 108164.CrossRefGoogle Scholar