Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-10T05:02:58.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of turbulent slope flows up to Grashof number $Gr=2.1\times 10^{11}$

Published online by Cambridge University Press:  22 September 2017

M. G. Giometto Open the ORCID record for M. G. Giometto [Opens in a new window] ,
G. G. Katul ,
J. Fang  and
M. B. Parlange
M. G. Giometto*
Affiliation:
Department of Civil Engineering, University of British Columbia, Vancouver, BC V6T 1Z4, Canada
G. G. Katul
Affiliation:
Nicholas School of the Environment, Duke University, Durham, NC 27708, USA
J. Fang
Affiliation:
School of Architecture, Civil and Environmental Engineering, École Polytechnique Fédérale de Lausanne, Lausanne, VD 1015, Switzerland
M. B. Parlange
Affiliation:
Department of Civil Engineering, University of British Columbia, Vancouver, BC V6T 1Z4, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Stably stratified turbulent flows over an unbounded, smooth, planar sloping surface at high Grashof numbers are examined using direct numerical simulations (DNS). Four sloping angles (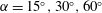$\unicode[STIX]{x1D6FC}=15^{\circ },30^{\circ },60^{\circ }$ and 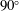$90^{\circ }$) and three Grashof numbers (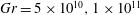$\mathit{Gr}=5\times 10^{10},1\times 10^{11}$ and 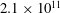$2.1\times 10^{11}$) are considered. Variations in mean flow, second-order statistics and budgets of mean- (MKE) and turbulent-kinetic energy (TKE) are evaluated as a function of $\unicode[STIX]{x1D6FC}$ and 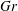$Gr$ at fixed molecular Prandtl number 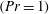$(Pr=1)$. Dynamic and energy identities are highlighted, which diagnose the convergence of the averaging operation applied to the DNS results. Turbulent anabatic (upward moving warm fluid along the slope) and katabatic (downward moving cold fluid along the slope) regimes are identical for the vertical wall set-up (up to the sign of the along-slope velocity), but undergo a different transition in the mechanisms sustaining turbulence as the sloping angle decreases, resulting in stark differences at low $\unicode[STIX]{x1D6FC}$. In addition, budget equations show how MKE is fed into the system through the imposed surface buoyancy, and turbulent fluctuations redistribute it from the low-level jet (LLJ) nose towards the boundary and outer flow regions. Analysis of the TKE budget equation suggests a subdivision of the boundary layer of anabatic and katabatic flows into four distinct thermodynamical regions: (i) an outer layer, corresponding approximately to the return flow region, where turbulent transport is the main source of TKE and balances dissipation; (ii) an intermediate layer, bounded below by the LLJ and capped above by the outer layer, where the sum of shear and buoyant production overcomes dissipation, and where turbulent and pressure transport terms are a sink of TKE; (iii) a buffer layer, located at 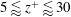$5\lessapprox z^{+}\lessapprox 30$, where TKE is provided by turbulent and pressure transport terms, to balance viscous diffusion and dissipation; and (iv) a laminar sublayer, corresponding to 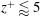$z^{+}\lessapprox 5$, where the influence of viscosity is significant. $(\cdot )^{+}$ denotes a quantity rescaled in inner units. Interestingly, a zone of global backscatter (energy transfer from the turbulent eddies to the mean flow) is consistently found in a thin layer below the LLJ in both anabatic and katabatic regimes.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Boundary Layers: Boundary layer structure Geophysical and Geological Flows: Meteorology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 589 - 620
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Department of Civil and Environmental Engineering, Monash University, Clayton, VIC 3800, Australia.

References

Abkar, M., Bae, H. J. & Moin, P. 2016 Minimum-dissipation scalar transport model for large-eddy simulation of turbulent flows. Phys. Rev. Fluids 1 (4), 041701.CrossRefGoogle Scholar
Albertson, J. D. & Parlange, M. B. 1999a Natural integration of scalar fluxes from complex terrain. Adv. Water Resour. 23 (3), 239–252.CrossRefGoogle Scholar
Albertson, J. D. & Parlange, M. B. 1999b Surface length scales and shear stress: implications for land-atmosphere interaction over complex terrain. Water Resour. Res. 35 (7), 2121–2132.Google Scholar
Arduini, G., Staquet, C. & Chemel, C. 2016 Interactions between the nighttime valley-wind system and a developing cold-air pool. Boundary-Layer Meteorol 161 (1), 49–72.CrossRefGoogle Scholar
Axelsen, S. & Dop, H. 2009a Large-eddy simulation of katabatic winds. Part 1: comparison with observations. Acta Geophys. 57 (4), 803–836.Google Scholar
Axelsen, S. L. & Dop, H. 2009b Large-eddy simulation of katabatic winds. Part 2: sensitivity study and comparison with analytical models. Acta Geophys. 57 (4), 837–856.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.Google Scholar
Bou-Zeid, E., Overney, J., Rogers, B. D. & Parlange, M. B. 2009 The effects of building representation and clustering in large-eddy simulations of flows in urban canopies. Boundary-Layer Meteorol. 132 (3), 415–436.Google Scholar
Burkholder, B., Fedorovich, E. & Shapiro, A. 2011 Evaluating subgrid-scale models for large-eddy simulation of turbulent katabatic flow. In Qual Reliab Large-eddy Simulations II, pp. 149–160. Springer.Google Scholar
Burkholder, B., Shapiro, A. & Fedorovich, E. 2009 Katabatic flow induced by a cross-slope band of surface cooling. Acta Geophys. 57 (4), 923–949.Google Scholar
Burns, P. & Chemel, C. 2014 Evolution of cold-air-pooling processes in complex terrain. Boundary-Layer Meteorol. 150 (3), 423–447.Google Scholar
Burns, P. & Chemel, C. 2015 Interactions between downslope flows and a developing cold-air pool. Boundary-Layer Meteorol. 154 (1), 57–80.Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22 (1), 015110.Google Scholar
Calaf, M., Parlange, M. B. & Meneveau, C. 2011 Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 23 (12), 126603.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2006 Spectral Methods. Springer.Google Scholar
Chamecki, M., Meneveau, C. & Parlange, M. B. 2009 Large eddy simulation of pollen transport in the atmospheric boundary layer. J. Aero. Sci. 40, 241–255.Google Scholar
Chemel, C., Staquet, C. & Largeron, Y. 2009 Generation of internal gravity waves by a katabatic wind in an idealized alpine valley. Meteorol. Atmos. Phys. 103 (1–4), 187–194.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22 (104), 745–762.Google Scholar
Chow, F. K., Weigel, A. P., Street, R. L., Rotach, M. W. & Xue, M. 2006 High-resolution large-eddy simulations of flow in a steep Alpine valley. Part I: Methodology, verification, and sensitivity experiments. J. Appl. Meteorol. Climatol. 45 (1), 63–86.Google Scholar
Chu, P. C. 1987 An instability theory of ice-air interaction for the formation of ice edge bands. J. Geophys. Res. 92 (C7), 6966–6970.CrossRefGoogle Scholar
Defant, F. 1949 Zur theorie der hangwinde, nebst bemerkungen zur theorie der berg- und talwinde. Arch. Meteorol. Geophys. Bioklimatol. Ser A 1, 421–450.Google Scholar
Denby, B. 1999 Second-order modelling of turbulence in katabatic flows. Boundary-Layer Meteorol. 92 (1), 65–98.Google Scholar
Doran, J. C. & Horst, T. W. 1981 Velocity and temperature oscillations in drainage winds. J. Appl. Meteorol. 20 (4), 361–364.Google Scholar
Egger, J. 1985 Slope winds and the axisymmetric circulation over Antarctica. J. Atmos. Sci. 42 (17), 1859–1867.Google Scholar
Fedorovich, E. & Shapiro, A. 2009 Structure of numerically simulated katabatic and anabatic flows along steep slopes. Acta Geophys. 57 (4), 981–1010.CrossRefGoogle Scholar
Fedorovich, E. & Shapiro, A. 2017 Oscillations in Prandtl slope flow started from rest. Q. J. R. Meteorol. Soc. 143 (703), 670–677.Google Scholar
Fernando, H. J. S. 2010 Fluid dynamics of urban atmospheres in complex terrain. Annu. Rev. Fluid Mech. 42 (1), 365–389.Google Scholar
Fernando, H. J. S., Pardyjak, E. R, Di Sabatino, S., Chow, F. K., De Wekker, S. F., Hoch, S. W., Hacker, J., Pace, J. C., Pratt, T., Pu, Z. et al. 2015 The MATERHORN: Unraveling the intricacies of mountain weather. Bull. Am. Meteorol. Soc. 96 (11), 1945–1967.Google Scholar
Giometto, M. G., Christen, A., Meneveau, C., Fang, J., Krafczyk, M. & Parlange, M. B. 2016 Spatial characteristics of roughness sublayer mean flow and turbulence over a realistic urban surface. Boundary-Layer Meteorol. 160 (3), 425–452.Google Scholar
Giometto, M. G., Grandi, R., Fang, J., Monkewitz, P. A. & Parlange, M. B. 2017 Katabatic flow: a closed-form solution with spatially-varying eddy diffusivities. Boundary-Layer Meteorol 162 (2), 307–317.CrossRefGoogle Scholar
Grachev, A. A., Leo, L. S., Sabatino, S. D., Fernando, H. J. S., Pardyjak, E. R. & Fairall, C. W. 2016 Structure of turbulence in katabatic flows below and above the wind-speed maximum. Boundary-Layer Meteorol. 159 (3), 469–494.Google Scholar
Greuell, J. W., Broeke Van den, M. R., Knap, W., Reijmer, C., Smeets, P. & Struijk, I.1994 PASTEX: a glacio-meteorological experiment on the Pasterze (Austria). Tech. Rep., Institute for Marine and Atmospheric Research, University, Utrecht.Google Scholar
Grisogono, B. & Axelsen, S. L. 2012 A note on the pure katabatic wind maximum over gentle slopes. Boundary-Layer Meteorol. 145 (3), 527–538.Google Scholar
Grisogono, B., Jurlina, T., Večenaj, Ž. & Güttler, I. 2014 Weakly nonlinear Prandtl model for simple slope flows. Q. J. R. Meteorol. Soc. 141, 883–892.Google Scholar
Grisogono, B., Kraljevic, L. & Jericevic, A. 2007 The low-level katabatic jet height versus Monin Obukhov height. Q. J. R. Meteorol. Soc. 133, 2133–2136.Google Scholar
Grisogono, B. & Oerlemans, J. 2001a A theory for the estimation of surface fluxes in simple katabatic flows. Q. J. R. Meteorol. Soc. 127, 2725–2739.Google Scholar
Grisogono, B & Oerlemans, J 2001b Katabatic flow: analytic solution for gradually varying eddy diffusivities. J. Atmos. Sci. 58 (21), 3349–3354.Google Scholar
Grisogono, B. & Oerlemans, J. 2002 Justifying the WKB approximation in pure katabatic flows. Tellus 54 (5), 453–462.Google Scholar
Gutman, L. N. 1983 On the theory of the katabatic slope wind. Tellus 35A, 213–218.CrossRefGoogle Scholar
Güttler, I., Marinović, I., Večenaj, Ž & Grisogono, B. 2016 Energetics of slope flows: linear and weakly nonlinear solutions of the extended Prandtl model. Front. Earth Sci. 4 (July), 1–13.Google Scholar
Haiden, T. & Whiteman, C. D. 2005 Katabatic flow mechanisms on a low-angle slope. J. Appl. Meteorol. 44 (1), 113–126.Google Scholar
Hang, C., Nadeau, D. F., Gultepe, I., Hoch, S. W., Román-Cascón, C., Pryor, K., Fernando, H. J. S., Creegan, E. D., Leo, L. S. & Silver, Z. 2016 A case study of the mechanisms modulating the evolution of valley fog. Pure Appl. Geophys. 173 (9), 1–20.Google Scholar
Higgins, C. W., Parlange, M. B. & Meneveau, C. 2003 Alignment trends of velocity gradients and subgrid-scale fluxes in the turbulent atmospheric boundary layer. Boundary-Layer Meteorol. 109 (1), 59–83.Google Scholar
Hultmark, M., Calaf, M. & Parlange, M. B. 2013 A new wall shear stress model for atmospheric boundary layer simulations. J. Atmos. Sci. 70 (11), 3460–3470.Google Scholar
Iida, O., Kasagi, N. & Nagano, Y. 2002 Direct numerical simulation of turbulent channel flow under stable density stratification. Intl J. Heat Mass Transfer 45, 1693–1703.Google Scholar
Israeli, M. & Orszag, S. A. 1981 Approximation of radiation boundary conditions. J. Comput. Phys. 41 (1), 115–135.Google Scholar
Jensen, D. D., Nadeau, D. F., Hoch, S. W. & Pardyjak, E. R. 2016 Observations of near-surface heat-flux and temperature profiles through the early evening transition over contrasting surfaces. Boundary-Layer Meteorol. 159 (3), 567–587.Google Scholar
Kavavcic, I. & Grisogono, B. 2007 Katabatic flow with Coriolis effect and gradually varying eddy diffusivity. Boundary-Layer Meteorol. 125 (2), 377–387.Google Scholar
Kravchenko, A. G. G. & Moin, P. 1997 On the effect of numerical errors in large eddy simulations of turbulent flows. J. Comput. Phys. 131 (2), 310–322.CrossRefGoogle Scholar
Kumar, V., Kleissl, J., Meneveau, C. & Parlange, M. B. 2006 Large-eddy simulation of a diurnal cycle of theatmospheric boundary layer: atmospheric stabilityand scaling issues. Water Resour. Res. 42, W06D09.Google Scholar
Lehner, M., Whiteman, C. D., Hoch, S. W., Jensen, D., Pardyjak, E. R., Leo, L. S., Di Sabatino, S. & Fernando, H. J. S. 2015 A case study of the nocturnal boundary layer evolution on a slope at the foot of a desert mountain. J. Appl. Meteorol. Climatol. 54 (4), 732–751.Google Scholar
Lu, H. & Porté-Agel, F. 2010 A modulated gradient model for large-eddy simulation: application to a neutral atmospheric boundary layer. Phys. Fluids 22 (1), 015109.Google Scholar
Mahrt, L. 1982 Momentum balance of gravity flows. J. Atmos. Sci. 39 (12), 2701–2711.Google Scholar
Mahrt, L. 1998 Stratified atmospheric boundary layers and breakdown of models. Theor. Comput. Fluid Dyn. 11, 263–279.Google Scholar
Mahrt, L. 2013 Stably stratified atmospheric boundary layers. Annu. Rev. Fluid Mech. 46 (July), 23–45.Google Scholar
McNider, R. T. 1982 A note on velocity fluctuations in drainage flows. J. Atmos. Sci. 39 (7), 1658–1660.Google Scholar
Menold, E. R. & Yang, K. 1962 Asymptotic solutions for unsteady laminar free convection on a vertical plate. J. Appl. Mech. 29 (1), 124–126.Google Scholar
Monti, P., Fernando, H. J. S. & Princevac, M. 2014 Waves and turbulence in katabatic winds. Environ. Fluid Mech. 14 (2), 431–450.Google Scholar
Monti, P., Fernando, H. J. S., Princevac, M., Chan, W. C., Kowalewski, T. A. & Pardyjak, E. R. 2002 Observations of flow and turbulence in the nocturnal boundary layer over a slope. J. Atmos. Sci. 59 (17), 2513–2534.Google Scholar
Moser, R. D., Kim, J. & Moin, P. 1999 Direct numerical simulation of turbulent channel flow up to Re = 590. Phys. Fluids 11 (4), 11–13.Google Scholar
Nadeau, D. F., Pardyjak, E. R., Higgins, C. W., Huwald, H. & Parlange, M. B. 2013a Flow during the evening transition over steep Alpine slopes. Q. J. R. Meteorol. Soc. 139 (672), 607–624.Google Scholar
Nadeau, D. F., Pardyjak, E. R., Higgins, C. W. & Parlange, M. B. 2013b Similarity scaling over a steep alpine slope. Boundary-Layer Meteorol. 147 (3), 401–419.Google Scholar
Oerlemans, J. 1998 The atmospheric boundary layer over melting glaciers. In Clear Cloudy Bound Layers, pp. 129–153. Royal Netherlands Academy of Arts and Sciences.Google Scholar
Oerlemans, J., Björnsson, H., Kuhn, M., Obleitner, F., Palsson, F., Smeets, C. J. P. P., Vugts, H. F. & Wolde, J. D. 1999 Glacio-meteorological investigation on Vatnajokull, Iceland, summer 1996: an overview. Boundary-Layer Meteorol. 92 (1), 3–24.Google Scholar
Oldroyd, H. J., Katul, G. G., Pardyjak, E. R. & Parlange, M. B. 2014 Momentum balance of katabatic flow on steep slopes covered with short vegetation. Geophys. Res. Lett. 41 (13), 4761–4768.Google Scholar
Oldroyd, H. J., Pardyjak, E. R., Higgins, C. W. & Parlange, M. B. 2016a Buoyant turbulent kinetic energy production in steep-slope katabatic flow. Boundary-Layer Meteorol. 161 (3), 405–416.Google Scholar
Oldroyd, H. J., Pardyjak, E. R., Huwald, H. & Parlange, M. B. 2016b Adapting tilt corrections and the governing flow equations for steep, fully three-dimensional, mountainous terrain. Boundary-Layer Meteorol. 159 (3), 539–565.Google Scholar
Orszag, S. A. 1969 Numerical methods for the simulation of turbulence. Phys. Fluids 12 (12), II–250.CrossRefGoogle Scholar
Orszag, S. A. 1970 Transform method for the calculation of vector-coupled sums: application to the spectral form of the vorticity equation. J. Atmos. Sci. 27 (6), 890–895.Google Scholar
Orszag, S. A. & Pao, Y. H. 1975 Numerical computation of turbulent shear flows. In Advances in Geophysics, vol. 18, pp. 225–236. Elsevier.Google Scholar
Parish, T. R. 1992 On the role of Antarctic katabatic winds in forcing large-scale tropospheric motions. J. Atmos. Sci. 49 (15), 1374–1385.Google Scholar
Parish, T. R. & Bromwich, D. H. 1998 A case study of Antarctic katabatic wind interaction with large-scale forcing. Mon. Weath. Rev. 126 (1), 199–209.Google Scholar
Parmhed, O., Oerlemans, J. & Grisogono, B. 2004 Describing surface fluxes in katabatic flow on Breidamerkurjo kull, Iceland. Q. J. R. Meteorol. Soc. 130, 1137–1151.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Porté-Agel, F., Meneveau, C. & Parlange, M. B. 2000 A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J. Fluid Mech. 415, 261–284.Google Scholar
Prandtl, L. 1942 Führer durch die Strömungslehre. Vieweg & Sohn.Google Scholar
Princevac, M., Hunt, J. C. R. & Fernando, H. J. S. 2008 Quasi-steady katabatic winds on slopes in wide valleys: hydraulic theory and observations. J. Atmos. Sci. 65 (2), 627–643.Google Scholar
Rampanelli, G., Zardi, D. & Rotunno, R. 2004 Mechanisms of up-valley winds. J. Atmos. Sci. 61 (24), 3097–3111.Google Scholar
Renfrew, I. A. 2004 The dynamics of idealized katabatic flow over a moderate slope and ice shelf. Q. J. R. Meteorol. Soc. 130 (598), 1023–1045.Google Scholar
Renfrew, I. A. & Anderson, P. S. 2006 Profiles of katabatic flow in summer and winter over Coats Land, Antarctica. Q. J. R. Meteorol. Soc. 132 (616), 779–802.Google Scholar
Rotach, M. W. & Zardi, D. 2007 On the boundary-layer structure over highly complex terrain: Key findings from MAP. Q. J. R. Meteorol. Soc. 133 (625), 937–948.Google Scholar
Schumann, U. 1990 Large-eddy simulation of the up-slope boundary layer. Q. J. R. Meteorol. Soc. 116 (493), 637–670.Google Scholar
Shah, S. K. & Bou-Zeid, E. 2014 Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics. J. Fluid Mech. 760, 494–539.Google Scholar
Shapiro, A. & Fedorovich, E. 2004 Prandtl number dependence of unsteady natural convection along a vertical plate in a stably stratified fluid. Intl J. Heat Mass Transfer 47 (22), 4911–4927.Google Scholar
Shapiro, A. & Fedorovich, E. 2005 Natural convection in a stably stratified fluid along vertical plates and cylinders with temporally periodic surface temperature variations. J. Fluid Mech. 546, 295–311.Google Scholar
Shapiro, A. & Fedorovich, E. 2007 Katabatic flow along a differentially cooled sloping surface. J. Fluid Mech. 571, 149–175.Google Scholar
Shapiro, A. & Fedorovich, E. 2008 Coriolis effects in homogeneous and inhomogeneous katabatic flows. Q. J. R. Meteorol. Soc. 134 (631), 353–370.Google Scholar
Shapiro, A. & Fedorovich, E. 2014 A boundary-layer scaling for turbulent katabatic flow. Boundary-Layer Meteorol. 153 (1), 1–17.Google Scholar
Sharma, V., Calaf, M., Lehning, M. & Parlange, M. B. 2016 Time-adaptive wind turbine model for an LES framework. Wind Energy 19 (5), 939–952.Google Scholar
Sharma, V., Parlange, M. B. & Calaf, M. 2017 Perturbations to the spatial and temporal characteristics of the diurnally-varying atmospheric boundary layer due to an extensive wind farm. Boundary-Layer Meteorol. 162 (2), 255–282.Google Scholar
Skyllingstad, E. D. 2003 Large-eddy simulation of katabatic flows. Boundary-Layer Meteorol. 106 (2), 217–243.Google Scholar
Smeets, C. J. P. P., Duynkerke, P. G. & Vugts, H. F. 1997 Turbulence characteristics of the stable boundary layer over a mid-latitude glacier. Part 1: a combination of katabatic and large-scale forcing. Boundary-Layer Meteorol. 87, 117–145.Google Scholar
Smeets, C. J. P. P., Duynkerke, P. G. & Vugts, H. F. 2000 Turbulence characteristics of the stable boundary layer over a mid-latitude glacier. Part 2: pure katabatic forcing conditions. Boundary-Layer Meteorol. 97, 73–107.Google Scholar
Smith, C. M. & Skyllingstad, E. D. 2005 Numerical simulation of katabatic flow with changing slope angle. Mon. Weath. Rev. 133 (11), 3065–3080.Google Scholar
Temam, R. 1968 Une methode d’approximation de la solution des equations de Navier–Stokes. Bull. Soc. Maths France 96, 115–152.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Weigel, A. P., Chow, F. K., Rotach, M. W., Street, R. L. & Xue, M. 2006 High-resolution large-eddy simulations of flow in a steep alpine valley. Part II: flow structure and heat budgets. J. Appl. Meteorol. Climatol. 45 (1), 87–107.Google Scholar
Whiteman, C. D. 1990 Observations of thermally developed wind systems in mountainous terrain. Atmos Process over complex terrain, Meteor. Monogr. 23 (45), 5–42.Google Scholar
Zardi, D. & Serafin, S. 2015 An analytic solution for time-periodic thermally driven slope flows. Q. J. R. Meteorol. Soc. 141, 1968–1974.Google Scholar
Zardi, D. & Whiteman, C. D. 2013 Diurnal mountain wind systems. In Mt Weather Res Forecast, pp. 35–119. Springer.Google Scholar