Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T12:02:05.511Z Has data issue: false hasContentIssue false
  • English
  • Français

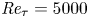Direct numerical simulation of thermal channel flow for ${\textit {Re}}_\tau =5000$ and 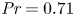${\textit {Pr}} = 0.71$

Published online by Cambridge University Press:  12 April 2021

Francisco Alcántara-Ávila Open the ORCID record for Francisco Alcántara-Ávila [Opens in a new window] ,
Sergio Hoyas Open the ORCID record for Sergio Hoyas [Opens in a new window]  and
María Jezabel Pérez-Quiles
Francisco Alcántara-Ávila
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada, Universitat Politècnica de València, Valencia46022, Spain
Sergio Hoyas*
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada, Universitat Politècnica de València, Valencia46022, Spain
María Jezabel Pérez-Quiles
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada, Universitat Politècnica de València, Valencia46022, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A direct numerical simulation of turbulent heat transfer in a channel flow has been conducted for a Reynolds number of $5000$ and the Prandtl number of air, $0.71$. The mixed boundary condition has been used as the boundary condition of the thermal field. The computational domain has been set to $3.2 {\rm \pi}h$, $2h$ and $1.6 {\rm \pi}h$ in the $x$, $y$ and $z$ directions, respectively. This domain is large enough to accurately compute the statistics of the flow. Mean values and intensities of the temperature have been obtained. Derived parameters from the average thermal field, such as the von Kármán constant and the Nusselt number have been calculated. An asymptotic behaviour of the von Kármán constant is observed when ${\textit {Re}}_\tau$ is increased. A correlation for the Nusselt number is proposed. Also, the turbulent Prandtl number has been calculated and it does not present significant changes when ${\textit {Re}}_\tau$ is increased. Finally, the turbulent budgets are presented. A relation between the increment of the inner peak of the temperature intensities and the scaling failure of the dissipation and viscous diffusion terms is provided. The statistics of all simulations can be downloaded from the web page of our group: http://personales.upv.es/serhocal/.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , A29
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, H. & Antonia, R.A. 2009 Turbulent Prandtl number in a channel flow for $Pr = 0.025$ and $0.71$. In Proceedings of the 6th International Symposium on Turbulence and Shear Flow Phenomena (ed. R. Friedrcih & A.V. Johansson), vol. 1, pp. 67–72. Seoul National University.Google Scholar
Abe, H. & Antonia, R.A. 2017 Relationship between the heat transfer law and the scalar dissipation function in a turbulent channel flow. J. Fluid Mech. 830, 300–325.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2004 Surface heat-flux fluctuations in a turbulent channel flow up to $Re_{\tau }=1020$ with $Pr=0.025$ and $0.71$. Intl J. Heat Fluid Flow 25 (3), 404–419.CrossRefGoogle Scholar
Alcántara-Ávila, F., Barberá, G. & Hoyas, S. 2019 Evidences of persisting thermal structures in couette flows. Intl J. Heat Fluid Flow 76, 287–295.CrossRefGoogle Scholar
Alcántara-Ávila, F. & Hoyas, S. 2020 Direct numerical simulation of thermal channel flow for medium–high Prandtl numbers up to $Re_\tau = 2000$. Intl J. Heat Mass Transfer (submitted).Google Scholar
Alcántara-Ávila, F., Hoyas, S. & Pérez-Quiles, M.J. 2018 DNS of thermal channel flow up to $Re_\tau =2000$ for medium to low Prandtl numbers. Intl J. Heat Mass Transfer 127, 349–361.CrossRefGoogle Scholar
Araya, G. & Castillo, L. 2012 DNS of turbulent thermal boundary layers up to $Re_\theta =2300$. Intl J. Heat Mass Transfer 55, 4003–4019.CrossRefGoogle Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & García-Galache, J.P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $Re_\tau =4000$. J. Fluid Mech. 758, 327–343.Google Scholar
Del Alamo, J.C., Jiménez, J., Zandonade, P. & Moser, R.D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Dittus, F.W. & Boelter, L.M.K. 1930 Heat Transfer in Automobile Radiators of the Tubular Type. Publications in Engineering, vol. 2, no. 13, pp. 443–461. University of California Press.Google Scholar
Gandía-Barberá, S., Hoyas, S., Oberlack, M. & Kraheberger, S. 2018 The link between the Reynolds shear stress and the large structures of turbulent Couette-Poiseuille flow. Phys. Fluids 30 (4), 041702.CrossRefGoogle Scholar
Gnielinski, V. 1976 New equations for heat and mass transfer in turbulent pipe and channel flow. Intl Chem. Engng 16, 359–367.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{\tau }=2003$. Phys. Fluids 18 (1), 011702.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.CrossRefGoogle Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Jiménez, J. & Moser, R.D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. Lond. A 365, 715–732.Google ScholarPubMed
Kasagi, N. & Ohtsubo, Y. 1993 Direct numerical simulation of low Prandtl number thermal field in a turbulent channel flow. In Turbulent Shear Flows (ed. F. Durst, R. Friedrich, B.E. Launder, F.W. Schmidt, U. Schumann & J.H. Whitelaw), vol. 8, pp. 97–119. Springer.CrossRefGoogle Scholar
Kasagi, N., Tomita, Y. & Kuroda, A. 1992 Direct numerical simulation of passive scalar field in a turbulent channel flow. Trans. ASME J. Heat Transfer 114 (3), 598–606.CrossRefGoogle Scholar
Kawamura, H., Abe, H. & Matsuo, Y. 1999 DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effects. Intl J. Heat Fluid Flow 20, 196–207.CrossRefGoogle Scholar
Kawamura, H., Ohsaka, K., Abe, H. & Yamamoto, K. 1998 DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluid. Intl J. Heat Fluid Flow 19 (5), 482–491.CrossRefGoogle Scholar
Kays, W.M., Crawford, M.E. & Weigand, B. 1980 Convective Heat and Mass Transfer. McGraw-Hill.Google Scholar
Kim, J. & Moin, P. 1987 Transport of passive scalars in a turbulent channel flow. NASA 1 (TM-89463), 1–14.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channels flows at low Reynolds numbers. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kozuka, M., Seki, Y. & Kawamura, H. 2009 DNS of turbulent heat transfer in a channel flow with a high spatial resolution. Intl J. Heat Fluid Flow 30 (3), 514–524.CrossRefGoogle Scholar
Lee, M. & Moser, R. 2015 Direct numerical simulation of turbulent channel flow up to $Re_\tau \approx 5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Lluesma-Rodríguez, F., Hoyas, S. & Peréz-Quiles, M.J. 2018 Influence of the computational domain on DNS of turbulent heat transfer up to $Re_\tau =2000$ for $Pr=0.71$. Intl J. Heat Mass Transfer 122, 983–992.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $Re_\tau = 4200$. Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Lyons, S.L., Hanratty, T.J. & McLaughlin, J.B. 1991 Direct numerical simulation of passive heat transfer in a turbulent channel flow. Intl J. Heat Mass Transfer 34 (4–5), 1149–1161.CrossRefGoogle Scholar
Moser, R.D., Kim, J. & Mansour, N.N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_\tau =590$. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Orszag, S.A. 1971 On the elimination of aliasing in finite difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28, 1074.2.0.CO;2>CrossRefGoogle Scholar
Piller, M., Nobile, E. & Hanratty, T.J. 2002 DNS study of turbulent transport at low Prandtl numbers in a channel flow. J. Fluid Mech. 458, 419–441.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.CrossRefGoogle Scholar
Sleicher, C.A. & Rouse, M.W. 1975 A convenient correlation for heat transfer to constant and variable property fluids in turbulent pipe flow. Intl J. Heat Mass Transfer 18, 677–683.CrossRefGoogle Scholar
Spalart, P.R., Moser, R.D. & Rogers, M.M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flows, 2nd ed. Cambridge University Press.Google Scholar
Yamamoto, Y. & Tsuji, Y. 2018 Numerical evidence of logarithmic regions in channel flow at $Re_\tau =8000$. Phys. Rev. Fluids 3, 012602(R).CrossRefGoogle Scholar
Yano, T. & Kasagi, N 1999 Direct numerical simulation of turbulent heat transport at high Prandtl numbers. JSME Intl J. B 42 (2), 284–292.CrossRefGoogle Scholar