Published online by Cambridge University Press: 26 November 2019
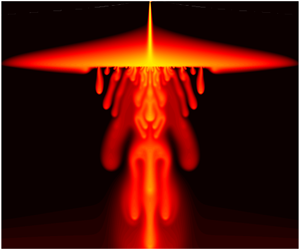
Thin, roughly horizontal low-permeability layers are a common form of large-scale heterogeneity in geological porous formations. In this paper, the dynamics of a buoyancy-driven plume in a two-dimensional layered porous medium is studied theoretically, with the aid of high-resolution numerical simulations. The medium is uniform apart from a thin, horizontal layer of a much lower permeability, located a dimensionless distance  $L\gg 1$ below the dense plume source. If the dimensionless thickness
$L\gg 1$ below the dense plume source. If the dimensionless thickness  $2\unicode[STIX]{x1D700}L$ and permeability
$2\unicode[STIX]{x1D700}L$ and permeability  $\unicode[STIX]{x1D6F1}$ of the low-permeability layer are small, the effect of the layer is found to be well parameterized by its impedance
$\unicode[STIX]{x1D6F1}$ of the low-permeability layer are small, the effect of the layer is found to be well parameterized by its impedance  $\unicode[STIX]{x1D6FA}=2\unicode[STIX]{x1D700}L/\unicode[STIX]{x1D6F1}$. Five different regimes of flow are identified and characterized. For
$\unicode[STIX]{x1D6FA}=2\unicode[STIX]{x1D700}L/\unicode[STIX]{x1D6F1}$. Five different regimes of flow are identified and characterized. For  $\unicode[STIX]{x1D6FA}\ll L^{1/3}$, the layer has no effect on the plume, but as
$\unicode[STIX]{x1D6FA}\ll L^{1/3}$, the layer has no effect on the plume, but as  $\unicode[STIX]{x1D6FA}$ is increased the plume widens and spreads over the layer as a gravity current. For still larger
$\unicode[STIX]{x1D6FA}$ is increased the plume widens and spreads over the layer as a gravity current. For still larger  $\unicode[STIX]{x1D6FA}$, the flow becomes destabilized by convective instabilities both below and above the layer, until, for
$\unicode[STIX]{x1D6FA}$, the flow becomes destabilized by convective instabilities both below and above the layer, until, for  $\unicode[STIX]{x1D6FA}\gg L$, the spread of the plume is dominated by convective mixing and buoyancy is transported across the layer by diffusion alone. Analytical models for the spread of the plume over the layer in the various different regimes are presented.
$\unicode[STIX]{x1D6FA}\gg L$, the spread of the plume is dominated by convective mixing and buoyancy is transported across the layer by diffusion alone. Analytical models for the spread of the plume over the layer in the various different regimes are presented.