Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T13:38:52.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy-driven flow in a confined aquifer with a vertical gradient of permeability

Published online by Cambridge University Press:  05 June 2018

Edward M. Hinton Open the ORCID record for Edward M. Hinton [Opens in a new window]  and
Andrew W. Woods Open the ORCID record for Andrew W. Woods [Opens in a new window]
Edward M. Hinton*
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the injection of fluid of one viscosity and density into a horizontal permeable aquifer initially saturated with a second fluid of different viscosity and density. The novel feature of the analysis is that we allow the permeability to vary vertically across the aquifer. This leads to recognition that the interface may evolve as either a rarefaction wave that spreads at a rate proportional to $t$, a shock-like front of fixed length or a mixture of shock-like regions and rarefaction-wave-type regions. The classical solutions in which there is no viscosity ratio between the fluids and in which the formation has constant permeability lead to an interface that spreads laterally at a rate proportional to 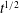$t^{1/2}$. However, these solutions are unstable to cross-layer variations in the permeability owing to the vertical shear which develops in the flow, causing the structure of the interface to evolve to the rarefaction wave or shock-like structure. In the case that the viscosities of the two fluids are different, it is possible that the solution involves a mixture of shock-like and rarefaction-type structures as a function of the distance above the lower boundary. Using the theory of characteristics, we develop a regime diagram to delineate the different situations. We consider the implications of such heterogeneity for the prediction of front locations during 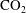$\text{CO}_{2}$ sequestration. If we neglect the permeability fluctuations, the model always predicts rarefaction-type solutions, while even modest changes in the permeability across a layer can introduce shocks. This difference may be very significant since it leads to the $\text{CO}_{2}$ plume occupying a greater fraction of the pore space between the injector and the leading edge of the 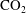$\text{CO}_{2}$ front in a layer of the same mean permeability. This has important implications for estimates of the fraction of the pore space that the 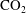$\text{CO}_{2}$ may access.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 411 - 429
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bachu, S. 2015 Review of CO2 storage efficiency in deep saline aquifers. Intl J. Greenh. Gas Control 40, 188–202.Google Scholar
Barenblatt, G. I. 1952 On some unsteady motions of fluids and gases in a porous medium. Prikl. Mat. Mekh. 16, 67–78.Google Scholar
Bear, J. 1971 Dynamics of Flow in Porous Media. Elsevier.Google Scholar
Bjorlykke, K. 1993 Fluid flow in sedimentary basins. Sedim. Geol. 86 (1–2), 137–158.Google Scholar
Carman, P. C. 1939 Permeability of saturated sands, soils and clays. J. Agric. Sci. 29, 262–273.Google Scholar
Celia, M. A., Bachu, S., Nordbotten, J. M. & Bandilla, K. W. 2015 Status of CO2 storage in deep saline aquifers with emphasis on modeling approaches and practical simulations. Water Resour. Res. 51 (9), 6846–6892.Google Scholar
Farcas, A. & Woods, A. W. 2016 Buoyancy-driven dispersion in a layered porous rock. J. Fluid Mech. 767, 226–239.CrossRefGoogle Scholar
Fayers, F. J., Blunt, M. J. & Christie, M. A. 1992 Comparisons of empirical viscous-fingering models and their calibration for heterogeneous problems. Soc. Petrol. Eng. 7, SPE-22184-PA.Google Scholar
Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.Google Scholar
Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.CrossRefGoogle Scholar
Guo, B., Bandilla, K. W., Nordbottten, J. M., Keilegavlen, E. & Doster, F. 2016a A multiscale multilayer vertically integrated model with vertical dynamic for CO2 sequestration in layered geological formations. Water Resour. Res. 52, 6490–6505.Google Scholar
Guo, B., Zheng, Z., Bandilla, K. W., Celia, M. A. & Stone, H. A. 2016b Flow regime analysis for geologic CO2 sequestration and other subsurface fluid injections. Intl J. Greenh. Gas Control 53, 284–291.CrossRefGoogle Scholar
Hesse, M. A., Tchelepi, H. A., Cantwel, B. J. & Orr, F. M. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363.CrossRefGoogle Scholar
Hesse, M., Tchelepi, H. A. & Orr, F. M.2006 Scaling analysis of the migration of $\text{CO}_{2}$ in saline aquifers. SPE Annual Technical Conference and Exhibition, 24-27 September, San Antonio, Texas, USA. Society of Petroleum Engineers. SPE-102796-MS.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
Hesse, M. A. & Woods, A. W. 2010 Buoyant dispersal of CO2 during geological storage. Geophys. Res. Lett. 37, L01403.CrossRefGoogle Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46 (1), 255–272.CrossRefGoogle Scholar
Huppert, H. E., Neufeld, J. A. & Strandkvist, C. 2013 The competition between gravity and flow focusing in two-layered porous media. J. Fluid Mech. 720, 5–14.Google Scholar
Juanes, R., MacMinn, C. W. & Szulczewski, M. L. 2010 The footprint of the CO2 plume during carbon dioxide storage in saline aquifers: storage efficiency for capillary trapping at the basin scale. Trans. Porous Med. 82 (1), 19–30.CrossRefGoogle Scholar
Kurganov, A. & Tadmor, E. 2000 New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations. J. Comput. Phys. 160 (1), 241–282.Google Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N., Salin, D. & Yortsos, Y. C. 1999 Miscible displacement in a Hele-Shaw cell at high rates. J. Fluid Mech. 398, 299–319.CrossRefGoogle Scholar
Lake, L. W. 1989 Enhanced Oil Recovery. Prentice Hall.Google Scholar
Lyu, X. & Woods, A. W. 2016 Experimental insights on the development of buoyant plumes injected into a porous media. Geophys. Res. Lett. 43 (2), 709–718.Google Scholar
MacMinn, C. W. & Juanes, R. 2009 Post-injection spreading and trapping of CO2 in saline aquifers: impact of the plume shape at the end of injection. Comput. Geosci. 13 (4), 483–491.Google Scholar
MacMinn, C. W., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2012 Spreading and convective dissolution of carbon dioxide in vertically confined, horizontal aquifers. Water Resour. Res. 48 (11), 1–11.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014 Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620.CrossRefGoogle Scholar
Pritchard, D., Woods, A. W. & Hogg, A. J. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444, 23–47.Google Scholar
Pruess, K., García, J., Kovscek, T., Oldenburg, C., Rutqvist, J., Steefel, C. & Xu, T. 2004 Code intercomparison builds confidence in numerical simulation models for geologic disposal of CO2 . Energy 29 (9–10), 1431–1444.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Taghavi, S. M., Seon, T., Martinez, D. M. & Frigaard, I. a. 2009 Buoyancy-dominated displacement flows in near-horizontal channels: the viscous limit. J. Fluid Mech. 639, 1–35.Google Scholar
Woods, A. W. 2014 Flow in Porous Rocks: Energy and Environmental Applications. Cambridge University Press.Google Scholar
Woods, A. W. & Farcas, A. 2009 Capillary entry pressure and the leakage of gravity currents through a sloping layered permeable rock. J. Fluid Mech. 618, 361.CrossRefGoogle Scholar
Zheng, Z., Guo, B., Christov, I. C., Celia, M. A. & Stone, H. A. 2015 Flow regimes for fluid injection into a confined porous medium. J. Fluid Mech. 767, 881–909.CrossRefGoogle Scholar