Published online by Cambridge University Press: 02 January 2013
In the ocean, sloping bottom topography is important for the generation and dissipation of internal waves. Here, the transition of such waves to turbulence is demonstrated using an accurate bottom-pressure sensor that was moored with an acoustic Doppler current profiler and high-resolution thermistor string on the sloping side of the ocean guyot ‘Great Meteor Seamount’ (water depth 549 m). The site is dominated by the passage of strong frontal bores, moving upslope once or twice every tidal period, with a trail of high-frequency internal waves. The bore amplitude and precise timing of bore passage vary every tide. A bore induces mainly non-hydrostatic pressure, while the trailing waves induce mainly internal hydrostatic pressure. These separate (internal wave) pressure terms are independently estimated using current and temperature data, respectively. In the bottom-pressure time series, the passage of a bore is barely visible, but the trailing high-frequency internal waves are. A bore is obscured by higher-frequency pressure variations up to 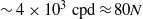 ${\sim} 4{\times} 1{0}^{3} ~\mathrm{cpd} \approx 80N$ (cpd, cycles per day;
${\sim} 4{\times} 1{0}^{3} ~\mathrm{cpd} \approx 80N$ (cpd, cycles per day; 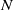 $N$, the large-scale buoyancy frequency). These motions dominate the turbulent state of internal tides above a sloping bottom. In contrast with previous bottom-pressure observations in other areas, infra-gravity surface waves contribute little to these pressure variations in the same frequency range. Here, such waves do not incur observed pressure. This is verified in a consistency test for large-Reynolds-number turbulence using high-resolution temperature data. The high-frequency quasi-turbulent internal motions are visible in detailed temperature and acoustic echo images, revealing a nearly permanently wave-turbulent tide going up and down the bottom slope. Over the entire observational period, the spectral slope and variance of bottom pressure are equivalent to internal hydrostatic pressure due to internal waves in the lower 100 m above the bottom, by non-hydrostatic pressure due to high-frequency internal waves and large-scale overturning. The observations suggest a transition between large-scale internal waves, small-scale internal tidal waves residing on thin (
$N$, the large-scale buoyancy frequency). These motions dominate the turbulent state of internal tides above a sloping bottom. In contrast with previous bottom-pressure observations in other areas, infra-gravity surface waves contribute little to these pressure variations in the same frequency range. Here, such waves do not incur observed pressure. This is verified in a consistency test for large-Reynolds-number turbulence using high-resolution temperature data. The high-frequency quasi-turbulent internal motions are visible in detailed temperature and acoustic echo images, revealing a nearly permanently wave-turbulent tide going up and down the bottom slope. Over the entire observational period, the spectral slope and variance of bottom pressure are equivalent to internal hydrostatic pressure due to internal waves in the lower 100 m above the bottom, by non-hydrostatic pressure due to high-frequency internal waves and large-scale overturning. The observations suggest a transition between large-scale internal waves, small-scale internal tidal waves residing on thin (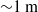 ${{\sim} }1~\mathrm{m} $) stratified layers and turbulence.
${{\sim} }1~\mathrm{m} $) stratified layers and turbulence.