Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-20T00:12:41.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Acoustic microstreaming produced by two interacting gas bubbles undergoing axisymmetric shape oscillations

Published online by Cambridge University Press:  26 November 2021

Alexander A. Doinikov ,
Gabriel Regnault ,
Cyril Mauger ,
Philippe Blanc-Benon  and
Claude Inserra Open the ORCID record for Claude Inserra [Opens in a new window]
Alexander A. Doinikov
Affiliation:
Univ Lyon, Collegium de Lyon, Ecole Centrale de Lyon, INSA Lyon, CNRS, LMFA UMR 5509, F-69002Lyon, France
Gabriel Regnault
Affiliation:
Univ Lyon, École Centrale de Lyon, INSA Lyon, CNRS, LMFA UMR 5509, F-69134Écully, France
Cyril Mauger
Affiliation:
Univ Lyon, École Centrale de Lyon, INSA Lyon, CNRS, LMFA UMR 5509, F-69134Écully, France
Philippe Blanc-Benon
Affiliation:
Univ Lyon, École Centrale de Lyon, INSA Lyon, CNRS, LMFA UMR 5509, F-69134Écully, France
Claude Inserra*
Affiliation:
Univ Lyon, Université Claude Bernard Lyon 1, Centre Léon Bérard, INSERM, UMR 1032, LabTAU, F-69003Lyon, France
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

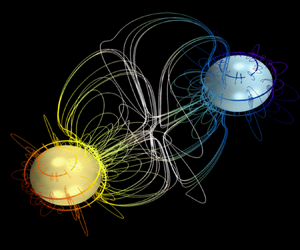
An analytical theory is developed that describes acoustic microstreaming produced by two interacting bubbles. The bubbles are assumed to undergo axisymmetric oscillation modes, which can include radial oscillations, translation and shape modes. Analytical solutions are derived in terms of complex amplitudes of oscillation modes, which means that the modal amplitudes are assumed to be known and serve as input data when the velocity field of acoustic microstreaming is calculated. No restrictions are imposed on the ratio of the bubble radii to the viscous penetration depth and the distance between the bubbles. The interaction between the bubbles is considered both when the linear velocity field is calculated and when the second-order velocity field of acoustic microstreaming is calculated. Capabilities of the analytical theory are illustrated by computational examples.

JFM classification

Drops and Bubbles: Bubble dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 931 , 25 January 2022 , A19
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I.A. 1972 Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. US Department of Commerce.Google Scholar
Bertin, N., Spelman, T.A., Combriat, T., Hue, H., Stéphan, O., Lauga, E. & Marmottant, P. 2017 Bubble-based acoustic micropropulsors: active surface and mixers. Lab on a Chip 17, 1515–1528.CrossRefGoogle Scholar
Bolanos-Jimenez, R., Rossi, M., Fernandez Rivas, D., Kähler, C.J. & Marin, A. 2017 Bubble-based acoustic micropropulsors: active surface and mixers. J. Fluid Mech. 820, 529–548.Google Scholar
Boyce, W.E. & DiPrima, R.C. 2001 Elementary Differential Equations and Boundary Value Problems. Wiley.Google Scholar
Doinikov, A.A. & Bouakaz, A. 2015 Theoretical model for coupled radial and translational motion of two bubbles at arbitrary separation distances. Phys. Rev. E 92, 043001.CrossRefGoogle ScholarPubMed
Doinikov, A.A. & Bouakaz, A. 2016 Microstreaming generated by two acoustically induced gas bubbles. J. Fluid Mech. 796, 318–339.CrossRefGoogle Scholar
Doinikov, A.A., Cleve, S., Regnault, G., Mauger, C. & Inserra, C. 2019 a Acoustic microstreaming produced by nonspherical oscillations of a gas bubble. I. Case of modes 0 and m. Phys. Rev. E 100, 033104.CrossRefGoogle Scholar
Doinikov, A.A., Cleve, S., Regnault, G., Mauger, C. & Inserra, C. 2019 b Acoustic microstreaming produced by nonspherical oscillations of a gas bubble. II. Case of modes 1 and m. Phys. Rev. E 100, 033105.CrossRefGoogle ScholarPubMed
Francescutto, A. & Nabergoj, R. 1978 Pulsation amplitude threshold for surface waves on oscillating bubbles. Acustica 41, 215–220.Google Scholar
Garbin, V., Cojoc, D., Ferrari, E., Di Fabrizio, D., Overvelde, M.L.J., van der Meer, S.M., de Jong, N., Lohse, D. & Versluis, M. 2007 Changes in microbubble dynamics near a boundary revealed by combined optical micromanipulation and high-speed imaging. Appl. Phys. Lett. 90, 114103.CrossRefGoogle Scholar
Guédra, M. & Inserra, C. 2018 Bubble shape oscillations of finite amplitude. J. Fluid Mech. 857, 681–703.CrossRefGoogle Scholar
Hall, P. & Seminara, G. 1980 Nonlinear oscillations of non-spherical cavitation bubbles in acoustic fields. J. Fluid Mech. 101, 423–444.CrossRefGoogle Scholar
Inserra, C., Regnault, G., Cleve, S., Mauger, C. & Doinikov, A.A. 2020 a Acoustic microstreaming produced by nonspherical oscillations of a gas bubble. III. Case of self-interacting modes n-n. Phys. Rev. E 101, 013111.CrossRefGoogle ScholarPubMed
Inserra, C., Regnault, G., Cleve, S., Mauger, C. & Doinikov, A.A. 2020 b Acoustic microstreaming produced by nonspherical oscillations of a gas bubble. IV. Case of modes n and m. Phys. Rev. E 102, 043103.CrossRefGoogle ScholarPubMed
Longuet-Higgins, M.S. 1998 Viscous streaming from an oscillating spherical bubble. Proc. R. Soc. Lond. Ser. A 454, 725–742.CrossRefGoogle Scholar
Mekki-Berrada, F., Combriat, T., Thibault, P. & Marmottant, P. 2016 Interactions enhance the acoustic streaming around flattened microfluidic bubbles. J. Fluid Mech. 797, 851–873.CrossRefGoogle Scholar
Mobadersany, N. & Sarkar, K. 2019 Acoustic microstreaming near a plane wall due to a pulsating free or coated bubble: velocity, vorticity and closed streamlines. J. Fluid Mech. 875, 781–806.CrossRefGoogle Scholar
Plesset, M.S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.CrossRefGoogle Scholar
Regnault, G., Mauger, C., Blanc-Benon, P. & Inserra, C. 2020 Secondary radiation force between two closely spaced acoustic bubbles. Phys. Rev. E 102, 031101.CrossRefGoogle ScholarPubMed
Shaw, S.J. 2006 Translation and oscillation of a bubble under axisymmetric deformation. Phys. Fluids 18, 072104.CrossRefGoogle Scholar
Tho, P., Manasseh, R. & Ooi, A. 2007 Cavitation microstreaming patterns in single and multiple bubble systems. J. Fluid Mech. 576, 191–233.CrossRefGoogle Scholar
Varshalovich, D.A., Moskalev, A.N. & Khersonskii, V.K. 1988 Quantum Theory of Angular Momentum. World Scientific.CrossRefGoogle Scholar
Wang, C. & Cheng, J. 2013 Cavitation microstreaming generated by a bubble pair in an ultrasound field. J. Acoust. Soc. Am. 134, 1675–1682.CrossRefGoogle Scholar
Westervelt, P.J. 1953 The theory of steady rotational flow generated by a sound field. J. Acoust. Soc. Am. 25, 60–67.CrossRefGoogle Scholar
Zwillinger, D. 2003 Standard Mathematical Tables and Formulae. CRC Press.Google Scholar