Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T19:37:27.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal control of a dam using Pλ,τM policies and penalty cost when the input process is a compound Poisson process with positive drift

Part of: Markov processes Special processes

Published online by Cambridge University Press:  14 July 2016

Mohamed Abdel-Hameed
Mohamed Abdel-Hameed*
Affiliation:
United Arab Emirates University
*
∗Postal address: Department of Statistics, College of Business and Economics, United Arab Emirates University, PO Box 17555 Al-Ain, United Arab Emirates. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

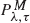In this paper we consider the optimal control of an infinite dam using policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.

Keywords

P^M_λ,τ policiespotentialinfinitesimal generatorcompound Poisson process with positive drifttotal discounted costlong-run average coststationary distribution

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces
Secondary: 60K25: Queueing theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 37 , Issue 2 , June 2000 , pp. 408 - 416
Copyright
Copyright © by the Applied Probability Trust 2000 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-Hameed, M. S. (1984). Life distribution properties of devices subject to a Lévy wear process. Math. Operat. Res. 9, 606–614.CrossRefGoogle Scholar
Abdel-Hameed, M. S. (1987). Inspection and maintenance of devices subject to deterioration. Adv. Appl. Prob. 19, 917–931.CrossRefGoogle Scholar
Abdel-Hameed, M. S., and Nakhi, Y. (1990). Optimal control of a finite dam using P_Λ,τM policies and penalty cost: total discounted and long run average cases. J. Appl. Prob. 27, 888–898.Google Scholar
Abdel-Hameed, M. S., and Nakhi, Y. (1991). Optimal replacement and maintenance of systems subject to semi-Markov damage. Stoch. Proc. Appl. 37, 141–160.CrossRefGoogle Scholar
Blumenthal, R. M., and Getoor, R. K. (1968). Markov Processes and Potential Theory. Academic Press, New York.Google Scholar
Karlin, S., and Taylor, H. W. (1981). A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
Lam, Y., and Lou, J. H. (1987). Optimal control of a finite dam. J. Appl. Prob. 24, 196–199.Google Scholar
Lamperti, J. (1977). Stochastic Processes: A Survey of the Mathematical Theory. Springer, New York.CrossRefGoogle Scholar
Lee, E. Y., and Ahn, S. K. (1998). P_τM-Policy for a dam with input formed by a compound Poisson process. J. Appl. Prob. 35, 482–488.Google Scholar
Zuckerman, D. (1977). Two-stage output procedure of a finite dam. J. Appl. Prob. 14, 421–425.CrossRefGoogle Scholar