Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Sepanski, Steven J.
1994.
Probabilistic characterizations of the Generalized Domain of Attraction of the multivariate normal law.
Journal of Theoretical Probability,
Vol. 7,
Issue. 4,
p.
857.
Gine, Evarist
1997.
Lectures on Probability Theory and Statistics.
Vol. 1665,
Issue. ,
p.
37.
Liu, Quansheng
and
Rouault, Alain
1997.
Classical and Modern Branching Processes.
Vol. 84,
Issue. ,
p.
187.
Chauvin, B.
and
Rouault, A.
1997.
Classical and Modern Branching Processes.
Vol. 84,
Issue. ,
p.
41.
Giné, Evarist
Götze, Friedrich
and
Mason, David M.
1997.
When is the Student $t$-statistic asymptotically standard normal?.
The Annals of Probability,
Vol. 25,
Issue. 3,
Račkauskas, Alfredas
and
Suquet, Charles
2001.
Invariance principles for adaptive self-normalized partial sums processes.
Stochastic Processes and their Applications,
Vol. 95,
Issue. 1,
p.
63.
Mason, David M.
and
Shao, Qi-Man.
2001.
Bootstrapping the Student t-Statistic.
The Annals of Probability,
Vol. 29,
Issue. 4,
CsõRGõ, MiklÓS
2002.
A glimpse of the impact of pál erd#ous on probability and statistics.
Canadian Journal of Statistics,
Vol. 30,
Issue. 4,
p.
493.
Kruglov, V. M.
and
Petrovskaya, G. N.
2002.
Weak Convergence of a Certain Functional.
Theory of Probability & Its Applications,
Vol. 46,
Issue. 4,
p.
721.
Csörgő, Miklós
Szyszkowicz, Barbara
and
Wu, Qiying
2003.
Donsker's theorem for self-normalized partial sums processes.
The Annals of Probability,
Vol. 31,
Issue. 3,
Račkauskas, Alfredas
and
Suquet, Charles
2004.
Hölder norm test statistics for epidemic change.
Journal of Statistical Planning and Inference,
Vol. 126,
Issue. 2,
p.
495.
Neves, Cláudia
Picek, Jan
and
Fraga Alves, M.I.
2006.
The contribution of the maximum to the sum of excesses for testing max-domains of attraction.
Journal of Statistical Planning and Inference,
Vol. 136,
Issue. 4,
p.
1281.
Ladoucette, Sophie A.
and
Teugels, Jef L.
2007.
Asymptotics for Ratios with Applications to Reinsurance.
Methodology and Computing in Applied Probability,
Vol. 9,
Issue. 2,
p.
225.
Downey, Peter J.
and
Wright, Paul E.
2007.
The ratio of the extreme to the sum in a random sequence.
Extremes,
Vol. 10,
Issue. 4,
p.
249.
Martsynyuk, Yu. V.
2009.
Functional asymptotic confidence intervals for the slope in linear error-in-variables models.
Acta Mathematica Hungarica,
Vol. 123,
Issue. 1-2,
p.
133.
Jones, Owen
and
Rolls, David
2011.
A characterisation of, and hypothesis test for, continuous local martingales.
Electronic Communications in Probability,
Vol. 16,
Issue. none,
2011.
Extreme Value Methods with Applications to Finance.
Vol. 20114852,
Issue. ,
p.
351.
Choi, Jinho
2012.
Rate Allocation for Multipath Routing in Wireless Multihop Networks with Security Constraints Based on Erasure Channel Modeling.
IEEE Transactions on Communications,
Vol. 60,
Issue. 9,
p.
2689.
Decrouez, Geoffrey
and
Jones, Owen Dafydd
2012.
A class of multifractal processes constructed using an embedded branching process.
The Annals of Applied Probability,
Vol. 22,
Issue. 6,
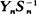 converges to zero in probability if and only if
converges to zero in probability if and only if 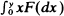 is slowly varying. This result implies that in a supercritical Galton-Watson process which does not become extinct, there cannot be a sequence {τ n} of particles, each descended from the preceding one, such that the fraction of all particles which are descendants of τ n does not converge to zero as n →∞. Weakly m-adic trees, which behave to some extent like sample Galton-Watson trees, can have such sequences of particles.
is slowly varying. This result implies that in a supercritical Galton-Watson process which does not become extinct, there cannot be a sequence {τ n} of particles, each descended from the preceding one, such that the fraction of all particles which are descendants of τ n does not converge to zero as n →∞. Weakly m-adic trees, which behave to some extent like sample Galton-Watson trees, can have such sequences of particles.