Let N(t) be a birth-death process on 𝒩= {0, 1, 2, ·· ·} governed by the transition rates λn > 0 (n ≧ 0) and μn > 0 (n ≧ 1) where λn → λ > 0 and μn → μ > 0 as n → ∞ and ρ = λ/μ. Let Tmn be the first-passage time of N(t) from m to n and define 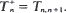It is shown that, when 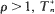converges in distribution to TBP(μ,λ) as n → ∞ where TΒΡ (μ,λ) is the server busy period of an M/M/1 queueing system with arrival rate μ and service rate λ. Correspondingly T0n/E[T0n] converges to 1 with probability 1 as n →∞. Of related interest is the conditional first-passage time mTrn of N(t) from r to n given no visit to m where m < r < n. As we shall see, the conditional first-passage time of N(t) can be viewed as an ordinary first-passage time of a modified birth-death process M(t) governed by 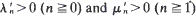where 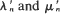are generated from λn and μn. Furthermore it is shown that for 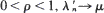and 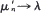while for 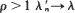and 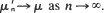This enables one to establish the relation between the limiting behavior of the ordinary first-passage times and that of the conditional first-passage times.