Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T22:16:14.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Cluster shock models

Published online by Cambridge University Press:  14 July 2016

Peter F. Thall
Peter F. Thall*
Affiliation:
George Washington University
*
∗Postal address: Department of Statistics, Bldg. C, Room 304, George Washington University, Washington, D.C. 20052, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

The survival distribution of a device subject to a sequence of shocks occurring randomly over time is studied by Esary, Marshall and Proschan (1973) and by A-Hameed and Proschan (1973), (1975). The present note treats the case in which shocks occur according to a homogeneous Poisson cluster process. It is shown that if 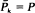[the device survives k shocks] = zk, 0 < z < 1, then the device exhibits a decreasing failure rate. A DFR preservation theorem is proved for completely monotonic 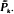. A counterexample to the IFR preservation theorem is given in which 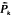is strictly IFR while the failure rate is initially decreasing and then increasing.

Keywords

RELIABILITYFAILURE RATEPRESERVATION THEOREMPOINT PROCESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 18 , Issue 1 , March 1981 , pp. 104 - 111
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A-Hameed, M. S. and Proschan, F. (1973) Nonstationary shock models. Stoch. Proc. Appl. 1, 383–404.CrossRefGoogle Scholar
A-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth process. J. Appl. Prob. 12, 18–28.CrossRefGoogle Scholar
Ammann, L. P. and Thall, P. F. (1977) On the structure of regular infinitely divisible point processes. Stoch. Proc. Appl. 6, 87–94.CrossRefGoogle Scholar
Ammann, L. P. and Thall, P. F. (1979) Count distributions, orderliness and invariance of Poisson cluster processes. J. Appl. Prob. 16, 261–273.Google Scholar
Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Reliability and Life Testing. Probability Models. Holt, Rinehart and Winston, New York.Google Scholar
Esary, J. D., Marshall, A. W. and Proschan, F. (1973) Shock models and wear processes. Ann. Prob. 1, 627–649.CrossRefGoogle Scholar
Gaver, D. P. Jr. (1963) Random hazard in reliability problems. Technometrics 5, 211–226.CrossRefGoogle Scholar
Jagers, P. (1973) On Palm probabilities. Z. Wahrscheinlichkeitsth. 26, 17–32.CrossRefGoogle Scholar
Karlin, S. (1968) Total Positivity, Vol. I. Stanford University Press, Stanford.Google Scholar
Karlin, S. and Proschan, F. (1960) Pólya type distributions of convolutions. Ann. Math. Statist. 31, 721–736.CrossRefGoogle Scholar
Matthes, K., Kerstan, J. and Mecke, J. (1978) Infinitely Divisible Point Processes. Wiley, New York.Google Scholar
Milne, R. K. and Westcott, M. (1972) Further results for the Gauss–Poisson process. Adv. Appl. Prob. 4, 151–176.CrossRefGoogle Scholar
Newman, D. S. (1970) A new family of point processes which are characterized by their second moment properties. J. Appl. Prob. 7, 338–358.CrossRefGoogle Scholar
Oakes, D. (1975) Synchronous and asynchronous distributions for Poisson cluster processes. J. R. Statist. Soc. B 37, 238–247.Google Scholar
Shohat, J. A. and Tamarkin, J. D. (1943) The Problem of Moments. American Mathematical Society, New York.CrossRefGoogle Scholar