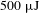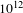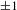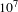1 Introduction
Peta watt (PW) level laser systems, with focused laser peak intensity of about
![]() $10^{22}~\text{W}/\text{cm}^{2}$
or even higher, have been reported repeatedly[Reference Aoyama, Yamakawa, Akahane, Ma, Inoue, Ueda and Kiriyama1–Reference Yu, Liang, Xu, Li, Peng, Hu, Wang, Lu, Chu, Gan, Liu, Liu, Wang, Lu, Yin, Leng, Li and Xu6]. These extremely high intensity conditions have aroused new interest in exploring laser–matter interactions, such as particle acceleration, bright X-ray source generation, and inertial confinement fusion[Reference Kiriyama, Mori, Pirozhkov, Ogura, Sagisaka, Kon, Esirkepov, Hayashi, Kotaki, Kanasaki, Sakaki, Fukuda, Koga, Nishiuchi, Kando, Bulanov, Kondo, Bolton, Slezak, Vojna, Sawicka-Chyla, Jambunathan, Lucianetti and Mocek7, Reference Salamin, Hu, Hatsagortsyan and Keitel8]. Temporal contrast is one of the crucial parameters of PW laser pulses. Prepulses with laser peak intensity higher than
$10^{22}~\text{W}/\text{cm}^{2}$
or even higher, have been reported repeatedly[Reference Aoyama, Yamakawa, Akahane, Ma, Inoue, Ueda and Kiriyama1–Reference Yu, Liang, Xu, Li, Peng, Hu, Wang, Lu, Chu, Gan, Liu, Liu, Wang, Lu, Yin, Leng, Li and Xu6]. These extremely high intensity conditions have aroused new interest in exploring laser–matter interactions, such as particle acceleration, bright X-ray source generation, and inertial confinement fusion[Reference Kiriyama, Mori, Pirozhkov, Ogura, Sagisaka, Kon, Esirkepov, Hayashi, Kotaki, Kanasaki, Sakaki, Fukuda, Koga, Nishiuchi, Kando, Bulanov, Kondo, Bolton, Slezak, Vojna, Sawicka-Chyla, Jambunathan, Lucianetti and Mocek7, Reference Salamin, Hu, Hatsagortsyan and Keitel8]. Temporal contrast is one of the crucial parameters of PW laser pulses. Prepulses with laser peak intensity higher than
![]() $10^{10}~\text{W}/\text{cm}^{2}$
[Reference Corkum, Brunel, Sherman and Srinivasanrao9, Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry10] in advance of the main pulse should be avoided as they can pre-ionize the target and generate a low density preplasma before the main pulse reaches the target.
$10^{10}~\text{W}/\text{cm}^{2}$
[Reference Corkum, Brunel, Sherman and Srinivasanrao9, Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry10] in advance of the main pulse should be avoided as they can pre-ionize the target and generate a low density preplasma before the main pulse reaches the target.
To build high temporal contrast laser systems, optical parametric chirped-pulse amplification (OPCPA)[Reference Kiriyama, Mori, Nakai, Yamamoto, Tanoue, Akutsu, Shimomura, Kondo, Kanazawa, Daido, Kimura and Miyanaga11, Reference Kiriyama, Mori, Nakai, Shimomura, Tanoue, Akutsu, Kondo, Kanazawa, Okada, Motomura, Daido, Kimura and Tajima12] and double chirped-pulse amplification (double CPA)[Reference Wang, Liu, Shen, Zhang, Teng and Wei3, Reference Kalashnikov, Risse, Schonnagel and Sandner13, Reference Xie, Zhou, Huang, Wang, Sun, Guo and Li14] combined with pulse cleaning techniques have been proposed in the past decades. These pulse cleaning techniques include saturable absorbers[Reference Kiriyama, Mori, Nakai, Shimomura, Sasao, Tanoue, Kanazawa, Wakai, Sasao, Okada, Daito, Suzuki, Kondo, Kondo, Sugiyama, Bolton, Yokoyama, Daido, Kawanishi, Kimura and Tajima15], optical parametric amplification[Reference Wang, Liu, Shen, Zhang, Teng and Wei3, Reference Huang, Zhang, Xu, Li, Leng, Li and Xu16], polarization rotation[Reference Kalashnikov, Risse, Schonnagel and Sandner13, Reference Homoelle, Gaeta, Yanovsky and Mourou17], and cross-polarized wave (XPW) generation[Reference Yanovsky, Chvykov, Kalinchenko, Rousseau, Planchon, Matsuoka, Maksimchuk, Nees, Cheriaux, Mourou and Krushelnick18–Reference Jullien, Albert, Burgy, Hamoniaux, Rousseau, Chambaret, Auge-Rochereau, Cheriaux, Etchepare, Minkovski and Saltiel20]. Pulse cleaning by using a self-diffraction (SD) process in a bulk Kerr medium was proposed recently[Reference Li, Shen, Wang, Li, Liu, Wang and Li21, Reference Liu, Okamura, Kida and Kobayashi22].
In theory, the temporal contrast of the first-order SD signal is the cube of the temporal contrast of the incident pulse as
![]() $C_{SD\pm 1}\approx C_{in}^{3}$
, because the generated cleaned SD signals are spatially separated from the incident beams without use of any polarization discrimination devices. What is more, this technique can also achieve a high energy SD signal output using a cylinder mirror focusing on the incident beams, even with low energy-conversion efficiency[Reference Li, Shen, Wang, Li, Liu, Wang and Li21]. These two advantages make the SD process a good choice for providing seed pulses for PW laser systems. However, the angular dispersion of the SD signals may affect the pulse compression of the amplified pulse in the compressor.
$C_{SD\pm 1}\approx C_{in}^{3}$
, because the generated cleaned SD signals are spatially separated from the incident beams without use of any polarization discrimination devices. What is more, this technique can also achieve a high energy SD signal output using a cylinder mirror focusing on the incident beams, even with low energy-conversion efficiency[Reference Li, Shen, Wang, Li, Liu, Wang and Li21]. These two advantages make the SD process a good choice for providing seed pulses for PW laser systems. However, the angular dispersion of the SD signals may affect the pulse compression of the amplified pulse in the compressor.
In this study, we report the highest pulse energy and highest temporal contrast enhancement pulses generation based on the SD effect with two cylindrical convex lenses so far. More than
![]() $500~\unicode[STIX]{x03BC}\text{J}$
first-order SD signal with a temporal contrast of
$500~\unicode[STIX]{x03BC}\text{J}$
first-order SD signal with a temporal contrast of
![]() $10^{12}$
is generated with about five orders of magnitude improvement. The wings around the main pulse in
$10^{12}$
is generated with about five orders of magnitude improvement. The wings around the main pulse in
![]() $\pm 1$
ps are cleaned with a contrast improvement of about
$\pm 1$
ps are cleaned with a contrast improvement of about
![]() $10^{7}$
, which verifies the pulse cleaning ability of SD process. The cause of angular dispersion generation of the SD signals is also explored, and the linear angular dispersion is compensated with a single prism.
$10^{7}$
, which verifies the pulse cleaning ability of SD process. The cause of angular dispersion generation of the SD signals is also explored, and the linear angular dispersion is compensated with a single prism.
2 Principle and experimental setup
The SD process is a degenerated cascaded four-wave mixing (DCFWM) process[Reference Li, Shen, Wang, Li, Liu, Wang and Li21–Reference Liu and Kobayashi23]. It acts as a temporal gating to improve the temporal contrast of a laser pulse. As an instantaneous third-order nonlinear optical effect, the SD process happened in hundreds of femtosecond time scale which requires a relatively high laser intensity at the same time. Weak satellite pulses and amplified spontaneous emission (ASE) noise can be filtered out by this process[Reference Li, Shen, Wang, Li, Liu, Wang and Li21]. In the time domain, the intensity of the first-order SD signal has the relationship to the intensities of the two input beams as
![]() $I_{SD+1}\propto I_{+1}^{2}(t)I_{-1}(t-\unicode[STIX]{x1D70F})$
, where
$I_{SD+1}\propto I_{+1}^{2}(t)I_{-1}(t-\unicode[STIX]{x1D70F})$
, where
![]() $\unicode[STIX]{x1D70F}$
is the time delay between the two input pulses[Reference Vinetskii, Kukhtarev, Odulov and Soskin24]. According to the equation, the temporal contrast of the
$\unicode[STIX]{x1D70F}$
is the time delay between the two input pulses[Reference Vinetskii, Kukhtarev, Odulov and Soskin24]. According to the equation, the temporal contrast of the
![]() $SD_{+1}$
signal is the cube of that of the incident pulse
$SD_{+1}$
signal is the cube of that of the incident pulse
![]() $C_{SD+1}\approx C_{in}^{3}$
. Furthermore, the generated signals and incident beams are separated spatially, which means no polarizer with a limited extinction ratio is needed, which is a main limitation for the XPW process. These properties indicate a potential high temporal contrast enhancement by using the SD process.
$C_{SD+1}\approx C_{in}^{3}$
. Furthermore, the generated signals and incident beams are separated spatially, which means no polarizer with a limited extinction ratio is needed, which is a main limitation for the XPW process. These properties indicate a potential high temporal contrast enhancement by using the SD process.
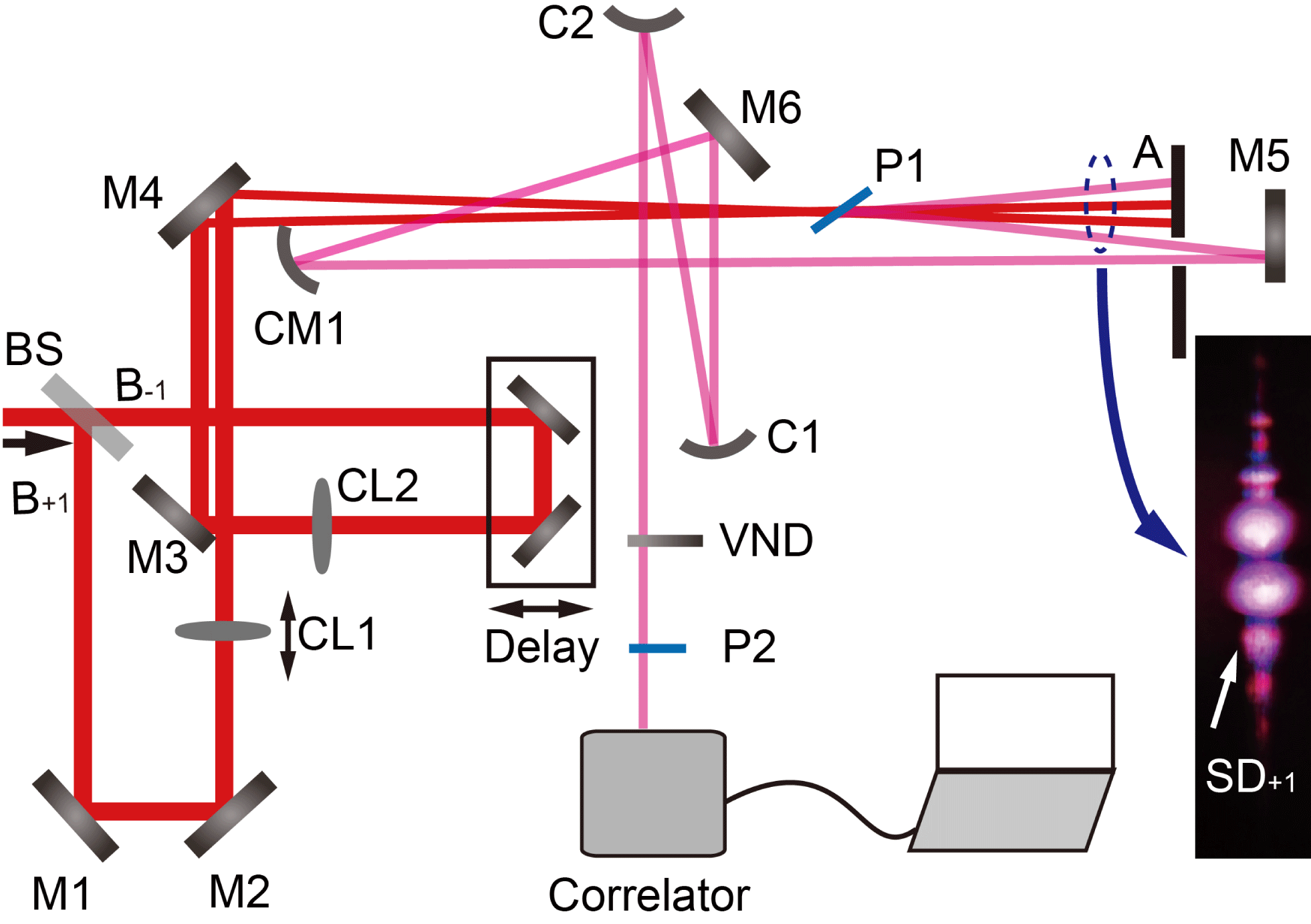
Figure 1. Experimental setup for self-diffraction signal generation and temporal contrast measurement. BS: beam splitter; M1–M6: reflective mirrors; CL1, CL2: plane-convex cylindrical lenses,
![]() $f=500$
mm; P1: 0.15 mm thick fused silica plate; A: aperture; CM1: cylindrical reflective mirror,
$f=500$
mm; P1: 0.15 mm thick fused silica plate; A: aperture; CM1: cylindrical reflective mirror,
![]() $f=500$
mm; C1: spherical concave reflective mirror,
$f=500$
mm; C1: spherical concave reflective mirror,
![]() $f=-500$
mm; C2: spherical convex reflective mirror,
$f=-500$
mm; C2: spherical convex reflective mirror,
![]() $f=200$
mm; VND: 2 mm thick variable neutral-density filter; P2: 1 mm thick fused silica plate; correlator: third-order cross-correlator (Amplitude Technologies Inc., Sequia 800).
$f=200$
mm; VND: 2 mm thick variable neutral-density filter; P2: 1 mm thick fused silica plate; correlator: third-order cross-correlator (Amplitude Technologies Inc., Sequia 800).
Figure 1 shows the experimental setup. Pulses from a laser system are separated into two beams
![]() $B_{+}$
and
$B_{+}$
and
![]() $B_{-}$
by a 50/50 beam splitter. Both
$B_{-}$
by a 50/50 beam splitter. Both
![]() $B_{+}$
and
$B_{+}$
and
![]() $B_{-}$
are separately focused into a Kerr medium P1 by two plane-convex cylindrical lenses CL1 and CL2. There is a delay line in the path of
$B_{-}$
are separately focused into a Kerr medium P1 by two plane-convex cylindrical lenses CL1 and CL2. There is a delay line in the path of
![]() $B_{-}$
. P1 is a 0.15 mm thick fused silica plate which is located about 60 mm behind the focus of the two lenses with a near Brewster angle to the two incident beams. The external crossing angle
$B_{-}$
. P1 is a 0.15 mm thick fused silica plate which is located about 60 mm behind the focus of the two lenses with a near Brewster angle to the two incident beams. The external crossing angle
![]() $\unicode[STIX]{x1D703}$
between the two incident beams is about
$\unicode[STIX]{x1D703}$
between the two incident beams is about
![]() $1.6^{\circ }$
, where the phase-matching condition can be easily satisfied[Reference Li, Shen, Wang, Li, Liu, Wang and Li21]. SD signals are formed beside the two incident beams in the condition that the two beams are temporally and spatially overlapped. An aperture A filters out the first-order SD signal
$1.6^{\circ }$
, where the phase-matching condition can be easily satisfied[Reference Li, Shen, Wang, Li, Liu, Wang and Li21]. SD signals are formed beside the two incident beams in the condition that the two beams are temporally and spatially overlapped. An aperture A filters out the first-order SD signal
![]() $SD_{+1}$
, then
$SD_{+1}$
, then
![]() $SD_{+1}$
is collimated by a cylindrical reflective mirror CM1. The collimated
$SD_{+1}$
is collimated by a cylindrical reflective mirror CM1. The collimated
![]() $SD_{+1}$
beam is reduced in beam size to about 3 mm diameter by a spherical concave reflective mirror and a spherical convex reflective mirror, and is then taken to a commercial third-order cross-correlator (Amplitude Technologies Inc., Sequia 800) for temporal contrast measurement. A variable neutral-density (VND) filter is used to adjust the input energy into the correlator. P2 is inserted to create replicas of the main pulse of
$SD_{+1}$
beam is reduced in beam size to about 3 mm diameter by a spherical concave reflective mirror and a spherical convex reflective mirror, and is then taken to a commercial third-order cross-correlator (Amplitude Technologies Inc., Sequia 800) for temporal contrast measurement. A variable neutral-density (VND) filter is used to adjust the input energy into the correlator. P2 is inserted to create replicas of the main pulse of
![]() $SD_{+1}$
.
$SD_{+1}$
.
3 Results and discussion
3.1 High energy and high temporal contrast SD pulse generation
To generate SD signals with high energy and temporal contrast, experiments were performed with a commercial Ti:sapphire CPA laser system (Legend Elite Cryo PA, Coherent Inc.). The laser system produces 1 kHz/50 fs/800 nm/10 mJ pulses with a diameter of about 15 mm. The pulse energies of the two incident beams before the Kerr medium P1 are both about 4.9 mJ. The beam size on the Kerr medium is about
![]() $15~\text{mm}\times 1.2~\text{mm}$
. About five diffracted orders of SD signals are generated beside each side of the two incident beams. The first-order SD signals
$15~\text{mm}\times 1.2~\text{mm}$
. About five diffracted orders of SD signals are generated beside each side of the two incident beams. The first-order SD signals
![]() $SD_{+1}$
and
$SD_{+1}$
and
![]() $SD_{-1}$
are about
$SD_{-1}$
are about
![]() $780~\unicode[STIX]{x03BC}\text{J}$
and
$780~\unicode[STIX]{x03BC}\text{J}$
and
![]() $630~\unicode[STIX]{x03BC}\text{J}$
, respectively. The energy-conversion efficiency from the two incident beams to
$630~\unicode[STIX]{x03BC}\text{J}$
, respectively. The energy-conversion efficiency from the two incident beams to
![]() $SD_{+1}$
is about 7.8%.
$SD_{+1}$
is about 7.8%.
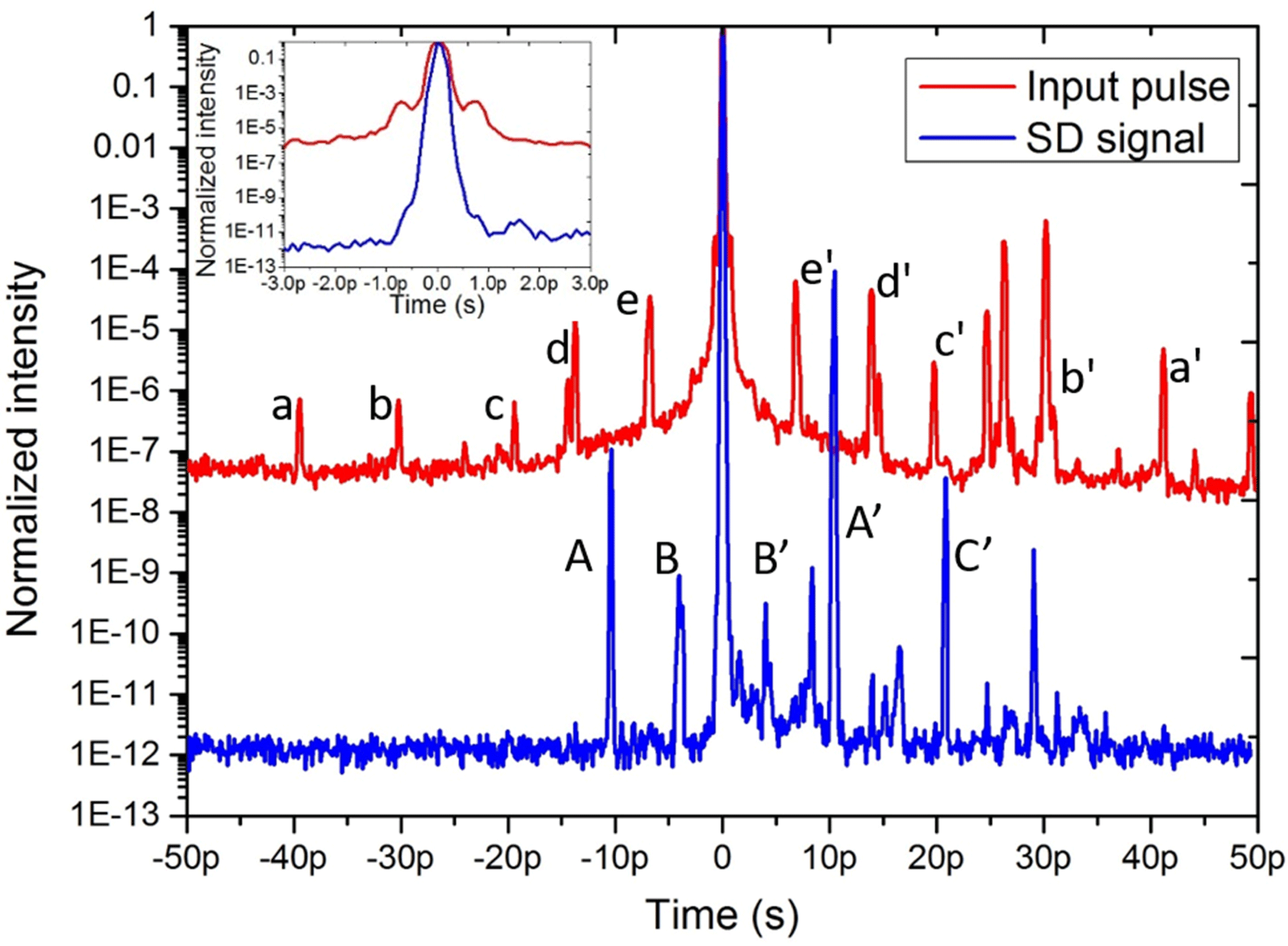
Figure 2. The temporal contrast of the input pulse and the generated first-order SD signal. The inset is an enlarged part of the curves from
![]() $-3$
ps to 3 ps.
$-3$
ps to 3 ps.
To characterize the temporal contrast of
![]() $SD_{+1}$
, the diameter of signal
$SD_{+1}$
, the diameter of signal
![]() $SD_{+1}$
beam is reduced to about 3 mm by C1 (spherical concave reflective mirror,
$SD_{+1}$
beam is reduced to about 3 mm by C1 (spherical concave reflective mirror,
![]() $f=-500$
) and C2 (spherical convex reflective mirror,
$f=-500$
) and C2 (spherical convex reflective mirror,
![]() $f=200$
mm) first. Then, a 2 mm thick VND filter is used to adjust the input energy to the correlator to about 200 mW. A 1 mm thick fused silica plate is inserted in the path of
$f=200$
mm) first. Then, a 2 mm thick VND filter is used to adjust the input energy to the correlator to about 200 mW. A 1 mm thick fused silica plate is inserted in the path of
![]() $SD_{+1}$
to introduce reference post-pulses.
$SD_{+1}$
to introduce reference post-pulses.
The measured temporal contrast curves of the input pulse and
![]() $SD_{+1}$
are shown in Figure 2. For the input pulse, before the main pulse, there are five replicas a/b/c/d/e with contrast varying from
$SD_{+1}$
are shown in Figure 2. For the input pulse, before the main pulse, there are five replicas a/b/c/d/e with contrast varying from
![]() $10^{6}$
to
$10^{6}$
to
![]() $10^{4}$
, and they are time symmetrical with replicas a’/b’/c’/d’/e’ after the main pulse, respectively. These replicas may come from reflection between front and rear surfaces of optical elements in the laser path. An amplified ASE-noise with contrast change from
$10^{4}$
, and they are time symmetrical with replicas a’/b’/c’/d’/e’ after the main pulse, respectively. These replicas may come from reflection between front and rear surfaces of optical elements in the laser path. An amplified ASE-noise with contrast change from
![]() $10^{7}$
to
$10^{7}$
to
![]() $10^{4}$
also exists around the main pulse. The 1 mm thick fused silica plate P2 introduces replicas A’ and C’ after the main pulse of
$10^{4}$
also exists around the main pulse. The 1 mm thick fused silica plate P2 introduces replicas A’ and C’ after the main pulse of
![]() $SD_{+1}$
with normalized intensity about
$SD_{+1}$
with normalized intensity about
![]() $10^{-4}$
and
$10^{-4}$
and
![]() $10^{-8}$
, respectively, which are about one order lower than the values introduced by the front and rear sides reflection of a fused silica plate. It may be caused by the tilt of P2, that the replicas and the main pulse are not collinear entirely. Replicas A and B are time symmetrical with replicas A’ and B’. From the inset in Figure 2, we can see that the SD process lasting just hundreds of femtosecond gated out all the replicas before the main pulse of the input pulse. Wings around the main pulse in
$10^{-8}$
, respectively, which are about one order lower than the values introduced by the front and rear sides reflection of a fused silica plate. It may be caused by the tilt of P2, that the replicas and the main pulse are not collinear entirely. Replicas A and B are time symmetrical with replicas A’ and B’. From the inset in Figure 2, we can see that the SD process lasting just hundreds of femtosecond gated out all the replicas before the main pulse of the input pulse. Wings around the main pulse in
![]() $\pm 1$
ps are cleaned with a contrast improvement of about
$\pm 1$
ps are cleaned with a contrast improvement of about
![]() $10^{7}$
, which verifies the pulse cleaning ability of SD process.
$10^{7}$
, which verifies the pulse cleaning ability of SD process.
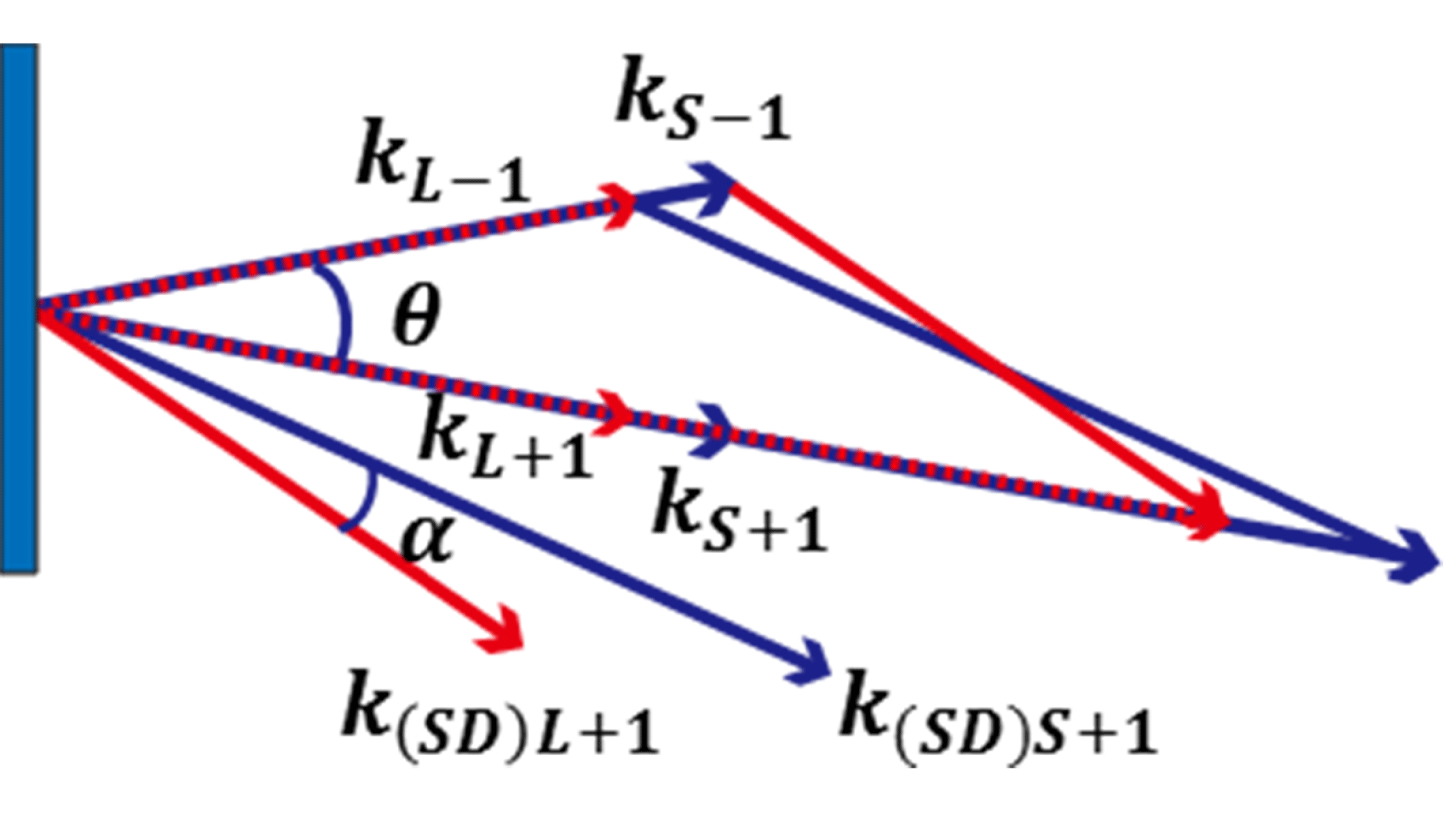
Figure 3. Scheme of angular dispersion generation.
3.2 Analyzation of angular dispersion generation
The generation of the angular dispersion of
![]() $SD_{+1}$
is caused by the different phase-matching condition of wavelength components of the two incident beams shown in Figure 3.
$SD_{+1}$
is caused by the different phase-matching condition of wavelength components of the two incident beams shown in Figure 3.
For
![]() $SD_{+1}$
, its phase-matching condition is
$SD_{+1}$
, its phase-matching condition is
![]() $\boldsymbol{k}_{SD+1}=2\boldsymbol{k}_{+1}-\boldsymbol{k}_{-1}$
. In the
$\boldsymbol{k}_{SD+1}=2\boldsymbol{k}_{+1}-\boldsymbol{k}_{-1}$
. In the
![]() $\boldsymbol{k}_{-1}$
direction,
$\boldsymbol{k}_{-1}$
direction,
![]() $\boldsymbol{k}_{L-1}$
denotes the wave vector of the longest wavelength component and
$\boldsymbol{k}_{L-1}$
denotes the wave vector of the longest wavelength component and
![]() $\boldsymbol{k}_{S-1}$
the wave vector of the shortest wavelength component. Similarly, in the
$\boldsymbol{k}_{S-1}$
the wave vector of the shortest wavelength component. Similarly, in the
![]() $\boldsymbol{k}_{+1}$
direction,
$\boldsymbol{k}_{+1}$
direction,
![]() $\boldsymbol{k}_{L+1}$
denotes the wave vector of the longest wavelength component and
$\boldsymbol{k}_{L+1}$
denotes the wave vector of the longest wavelength component and
![]() $\boldsymbol{k}_{S+1}$
the wave vector of the shortest wavelength component. Then the generated longest wavelength
$\boldsymbol{k}_{S+1}$
the wave vector of the shortest wavelength component. Then the generated longest wavelength
![]() $\unicode[STIX]{x1D706}_{NL}$
and shortest wavelength
$\unicode[STIX]{x1D706}_{NL}$
and shortest wavelength
![]() $\unicode[STIX]{x1D706}_{NS}$
in
$\unicode[STIX]{x1D706}_{NS}$
in
![]() $SD_{+1}$
can be expressed as
$SD_{+1}$
can be expressed as
![]() $\unicode[STIX]{x1D706}_{NL}=1/\text{sqrt}(\unicode[STIX]{x1D706}_{S}^{-2}+4\unicode[STIX]{x1D706}_{L}^{-2}-4\unicode[STIX]{x1D706}_{S}^{-1}\cdot \unicode[STIX]{x1D706}_{L}^{-1}\cdot \cos \unicode[STIX]{x1D703})$
and
$\unicode[STIX]{x1D706}_{NL}=1/\text{sqrt}(\unicode[STIX]{x1D706}_{S}^{-2}+4\unicode[STIX]{x1D706}_{L}^{-2}-4\unicode[STIX]{x1D706}_{S}^{-1}\cdot \unicode[STIX]{x1D706}_{L}^{-1}\cdot \cos \unicode[STIX]{x1D703})$
and
![]() $\unicode[STIX]{x1D706}_{NS}=1/\text{sqrt}(\unicode[STIX]{x1D706}_{L}^{-2}+4\unicode[STIX]{x1D706}_{S}^{-2}-4\unicode[STIX]{x1D706}_{S}^{-1}\cdot \unicode[STIX]{x1D706}_{L}^{-1}\cdot \cos \unicode[STIX]{x1D703})$
, respectively.
$\unicode[STIX]{x1D706}_{NS}=1/\text{sqrt}(\unicode[STIX]{x1D706}_{L}^{-2}+4\unicode[STIX]{x1D706}_{S}^{-2}-4\unicode[STIX]{x1D706}_{S}^{-1}\cdot \unicode[STIX]{x1D706}_{L}^{-1}\cdot \cos \unicode[STIX]{x1D703})$
, respectively.
![]() $\unicode[STIX]{x1D706}_{L}$
is the original longest and
$\unicode[STIX]{x1D706}_{L}$
is the original longest and
![]() $\unicode[STIX]{x1D706}_{S}$
the shortest wavelength of the incident pulses. The phase-matching conditions for the longest and shortest wavelength SD signals are
$\unicode[STIX]{x1D706}_{S}$
the shortest wavelength of the incident pulses. The phase-matching conditions for the longest and shortest wavelength SD signals are
![]() $\boldsymbol{k}_{(SD)L+1}=2\boldsymbol{k}_{L+1}-\boldsymbol{k}_{S-1}$
and
$\boldsymbol{k}_{(SD)L+1}=2\boldsymbol{k}_{L+1}-\boldsymbol{k}_{S-1}$
and
![]() $\boldsymbol{k}_{(SD)S+1}=2\boldsymbol{k}_{S+1}-\boldsymbol{k}_{L-1}$
, respectively. Then the dispersion angle
$\boldsymbol{k}_{(SD)S+1}=2\boldsymbol{k}_{S+1}-\boldsymbol{k}_{L-1}$
, respectively. Then the dispersion angle
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $SD_{+1}$
is the angle between
$SD_{+1}$
is the angle between
![]() $\boldsymbol{k}_{(SD)L+1}$
and
$\boldsymbol{k}_{(SD)L+1}$
and
![]() $\boldsymbol{k}_{(SD)S+1}$
. It is related to the cross angle of the two incident beams, the shortest and the longest wavelength components of the two beams, and can be expressed as
$\boldsymbol{k}_{(SD)S+1}$
. It is related to the cross angle of the two incident beams, the shortest and the longest wavelength components of the two beams, and can be expressed as
![]() $\unicode[STIX]{x1D6FC}=a-b$
,
$\unicode[STIX]{x1D6FC}=a-b$
,
![]() $a=\arcsin \{2k_{S+1}\sin \unicode[STIX]{x1D703}/\text{sqrt}[k_{L-1}^{2}+(2k_{S+1})^{2}-4k_{S+1}k_{L-1}\cos \unicode[STIX]{x1D703}]\}$
,
$a=\arcsin \{2k_{S+1}\sin \unicode[STIX]{x1D703}/\text{sqrt}[k_{L-1}^{2}+(2k_{S+1})^{2}-4k_{S+1}k_{L-1}\cos \unicode[STIX]{x1D703}]\}$
,
![]() $b=\arcsin \{2k_{L+1}\sin \unicode[STIX]{x1D703}/\text{sqrt}[k_{S-1}^{2}+(2k_{L+1})^{2}-4k_{S-1}k_{L+1}\cos \unicode[STIX]{x1D703}]\}$
.
$b=\arcsin \{2k_{L+1}\sin \unicode[STIX]{x1D703}/\text{sqrt}[k_{S-1}^{2}+(2k_{L+1})^{2}-4k_{S-1}k_{L+1}\cos \unicode[STIX]{x1D703}]\}$
.

Figure 4. (a) The spectra of the incident pulse and the first-order SD signal
![]() $SD_{+1}$
; (b) the
$SD_{+1}$
; (b) the
![]() $SD_{+1}$
spectra at 30 different positions, the inset shows the center wavelengths measured at each position.
$SD_{+1}$
spectra at 30 different positions, the inset shows the center wavelengths measured at each position.
There is a little difference between the center wavelength of
![]() $SD_{+1}$
and that of the incident pulses, and can be calculated according to the law of cosines:
$SD_{+1}$
and that of the incident pulses, and can be calculated according to the law of cosines:
![]() $\unicode[STIX]{x1D706}_{N}=\unicode[STIX]{x1D706}_{O}/\text{sqrt}(5-4\cos \unicode[STIX]{x1D703})$
, where
$\unicode[STIX]{x1D706}_{N}=\unicode[STIX]{x1D706}_{O}/\text{sqrt}(5-4\cos \unicode[STIX]{x1D703})$
, where
![]() $\unicode[STIX]{x1D706}_{N}$
is the new generated center wavelength of
$\unicode[STIX]{x1D706}_{N}$
is the new generated center wavelength of
![]() $SD_{+1}$
and
$SD_{+1}$
and
![]() $\unicode[STIX]{x1D706}_{O}$
the original center wavelength of the incident pulses. For
$\unicode[STIX]{x1D706}_{O}$
the original center wavelength of the incident pulses. For
![]() $\unicode[STIX]{x1D706}_{O}=803$
nm,
$\unicode[STIX]{x1D706}_{O}=803$
nm,
![]() $\unicode[STIX]{x1D703}=1.6^{\circ }$
. The new generated center wavelength of
$\unicode[STIX]{x1D703}=1.6^{\circ }$
. The new generated center wavelength of
![]() $SD_{+1}~\unicode[STIX]{x1D706}_{N}\approx 802.37$
nm. It can be concluded that for a small crossing angle of the two incident beams, the generated first-order SD signals almost keep the same center wavelength of the incident pulses, and the SD process can be looked on as a frequency-conserving process.
$SD_{+1}~\unicode[STIX]{x1D706}_{N}\approx 802.37$
nm. It can be concluded that for a small crossing angle of the two incident beams, the generated first-order SD signals almost keep the same center wavelength of the incident pulses, and the SD process can be looked on as a frequency-conserving process.
3.3 Angular dispersion compensation
For an incident beam with a spectrum as shown in Figure 4(a), its full width at half maximum (FWHM) spectrum width
![]() $w$
is about 28 nm with center wavelength at 803 nm. The generated dispersion angle
$w$
is about 28 nm with center wavelength at 803 nm. The generated dispersion angle
![]() $\unicode[STIX]{x1D6FC}\approx 3.90$
mrad according to the equation of
$\unicode[STIX]{x1D6FC}\approx 3.90$
mrad according to the equation of
![]() $\unicode[STIX]{x1D6FC}$
. Then the angular dispersion can be roughly calculated as
$\unicode[STIX]{x1D6FC}$
. Then the angular dispersion can be roughly calculated as
![]() $A_{c}=\unicode[STIX]{x1D6FC}/w\approx 0.14$
mrad/nm. The divergence angle caused by the lenses CL1 and CL2 with 500 mm focal length is about
$A_{c}=\unicode[STIX]{x1D6FC}/w\approx 0.14$
mrad/nm. The divergence angle caused by the lenses CL1 and CL2 with 500 mm focal length is about
![]() $\unicode[STIX]{x1D6FD}\approx \arcsin (6/500)\approx 12$
mrad. After about 2000 mm, the beam width of the
$\unicode[STIX]{x1D6FD}\approx \arcsin (6/500)\approx 12$
mrad. After about 2000 mm, the beam width of the
![]() $SD_{+1}$
is about
$SD_{+1}$
is about
![]() $l=2000~\text{mm}\times \sin (\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})\approx 32$
mm.
$l=2000~\text{mm}\times \sin (\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})\approx 32$
mm.
In the experiment, after propagation of about 2000 mm in air, the width of beam
![]() $SD_{+1}$
is about 30 mm. We measured the spectra of
$SD_{+1}$
is about 30 mm. We measured the spectra of
![]() $SD_{+1}$
at 30 different positions P0 to P29 in the horizontal direction, with every two positions separated by about 1 mm. Figure 4(b) shows the spectra measured at position P0/P4/P9/P14/P19/P24/P29 points. The curve of center wavelength measured at each position is presented in the insert figure in Figure 4(b). The center wavelength is shifted by about 20 nm. The angular dispersion measured can be roughly denoted as
$SD_{+1}$
at 30 different positions P0 to P29 in the horizontal direction, with every two positions separated by about 1 mm. Figure 4(b) shows the spectra measured at position P0/P4/P9/P14/P19/P24/P29 points. The curve of center wavelength measured at each position is presented in the insert figure in Figure 4(b). The center wavelength is shifted by about 20 nm. The angular dispersion measured can be roughly denoted as
![]() $A_{m}=[\arcsin (30/2000)-\unicode[STIX]{x1D6FD}]~\text{rad}/20~\text{nm}\approx 0.15~\text{mrad}/\text{nm}$
.
$A_{m}=[\arcsin (30/2000)-\unicode[STIX]{x1D6FD}]~\text{rad}/20~\text{nm}\approx 0.15~\text{mrad}/\text{nm}$
.
![]() $A_{m}\approx A_{c}$
, the measured result of the angular dispersion of generated SD signal matches very well with the theoretically calculated result.
$A_{m}\approx A_{c}$
, the measured result of the angular dispersion of generated SD signal matches very well with the theoretically calculated result.
The scheme of angular dispersion compensation is shown in Figure 5. A fused silica prism with apex angle
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/3$
rad is used to compensate the angular dispersion in our experiment. In beam
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/3$
rad is used to compensate the angular dispersion in our experiment. In beam
![]() $SD_{+1}$
, longer wavelength is located far away from the two incident beams and shorter wavelength located closer to the two incident beams. A cylindrical reflective mirror with focal length of 200 mm located 400 mm behind the Kerr medium P1 is used to symmetrically focus
$SD_{+1}$
, longer wavelength is located far away from the two incident beams and shorter wavelength located closer to the two incident beams. A cylindrical reflective mirror with focal length of 200 mm located 400 mm behind the Kerr medium P1 is used to symmetrically focus
![]() $SD_{+1}$
.
$SD_{+1}$
.
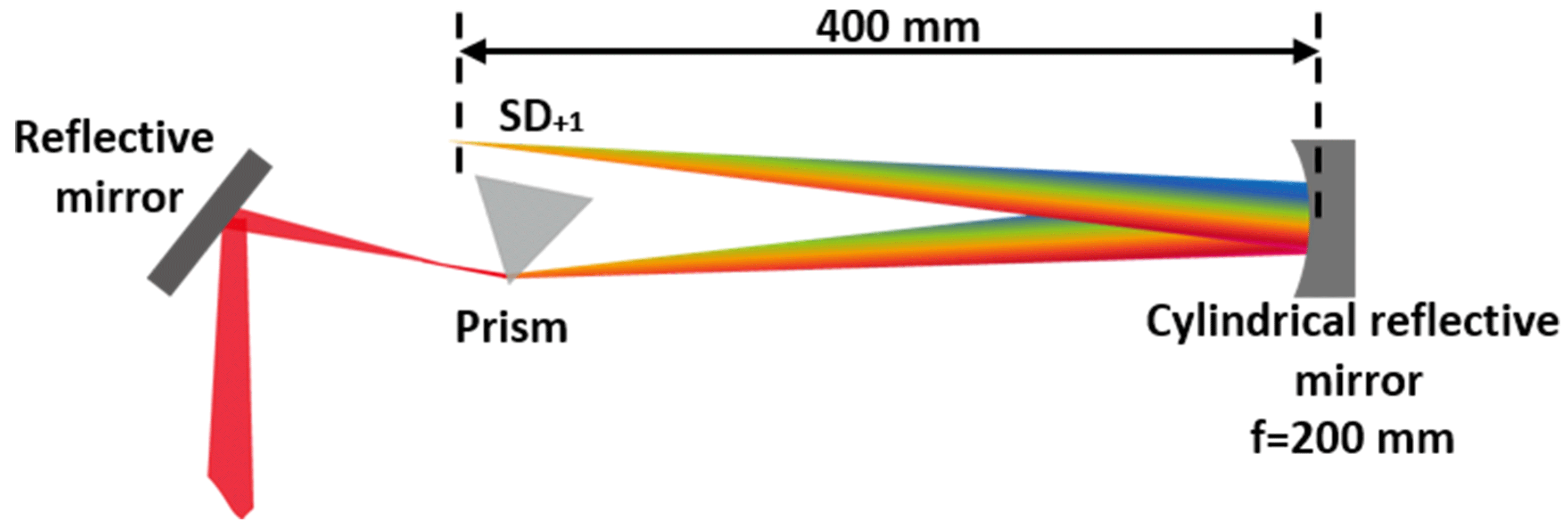
Figure 5. Scheme of angular dispersion compensation.
For a prism with refractive index
![]() $n$
and apex angle
$n$
and apex angle
![]() $\unicode[STIX]{x1D6FC}$
, we can obtain the angular dispersion of the prism[Reference Fork, Martinez and Gordon25] as
$\unicode[STIX]{x1D6FC}$
, we can obtain the angular dispersion of the prism[Reference Fork, Martinez and Gordon25] as
![]() $\text{d}\emptyset _{2}/\text{d}n=(\cos \emptyset _{2})^{-1}[\sin (\emptyset _{2}^{\prime })+\cos (\emptyset _{2}^{\prime })\tan (\emptyset _{1}^{\prime })]$
. According to the measurement, the angular dispersion of the generated
$\text{d}\emptyset _{2}/\text{d}n=(\cos \emptyset _{2})^{-1}[\sin (\emptyset _{2}^{\prime })+\cos (\emptyset _{2}^{\prime })\tan (\emptyset _{1}^{\prime })]$
. According to the measurement, the angular dispersion of the generated
![]() $SD_{+1}$
is about 0.15 mrad/nm with center wavelength shifting from 795 nm to 815 nm. We just consider the two edge center wavelengths
$SD_{+1}$
is about 0.15 mrad/nm with center wavelength shifting from 795 nm to 815 nm. We just consider the two edge center wavelengths
![]() $\unicode[STIX]{x1D706}_{NS}=795$
nm and
$\unicode[STIX]{x1D706}_{NS}=795$
nm and
![]() $\unicode[STIX]{x1D706}_{NL}=815$
nm here. We can calculate their refractive index according to Cauchy’s dispersion formula in the prism as
$\unicode[STIX]{x1D706}_{NL}=815$
nm here. We can calculate their refractive index according to Cauchy’s dispersion formula in the prism as
![]() $n_{NS}=1.4534$
and
$n_{NS}=1.4534$
and
![]() $n_{NL}=1.4531$
, respectively.
$n_{NL}=1.4531$
, respectively.
The relation between
![]() $\emptyset _{1}$
and
$\emptyset _{1}$
and
![]() $\emptyset _{2}$
can be calculated with Snell’s law
$\emptyset _{2}$
can be calculated with Snell’s law
![]() $\sin \emptyset _{1}=n\sin \emptyset _{1}^{\prime }$
,
$\sin \emptyset _{1}=n\sin \emptyset _{1}^{\prime }$
,
![]() $\sin \emptyset _{2}=n\sin \emptyset _{2}^{\prime }$
and
$\sin \emptyset _{2}=n\sin \emptyset _{2}^{\prime }$
and
![]() $\emptyset _{1}^{\prime }+\emptyset _{2}^{\prime }=\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/3$
rad. If the cross angle between the two output beams is about
$\emptyset _{1}^{\prime }+\emptyset _{2}^{\prime }=\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}/3$
rad. If the cross angle between the two output beams is about
![]() $\unicode[STIX]{x1D6FD}=0.15~\text{mrad}/\text{nm}\times 20~\text{nm}=3~\text{mrad}$
, the angle
$\unicode[STIX]{x1D6FD}=0.15~\text{mrad}/\text{nm}\times 20~\text{nm}=3~\text{mrad}$
, the angle
![]() $\emptyset _{1}=0.432~\text{rad}$
is the right output angle of the
$\emptyset _{1}=0.432~\text{rad}$
is the right output angle of the
![]() $SD_{+1}$
beam. The input angle of the
$SD_{+1}$
beam. The input angle of the
![]() $SD_{+1}$
beam can be calculated as about
$SD_{+1}$
beam can be calculated as about
![]() $\emptyset _{2}=1.481$
rad.
$\emptyset _{2}=1.481$
rad.
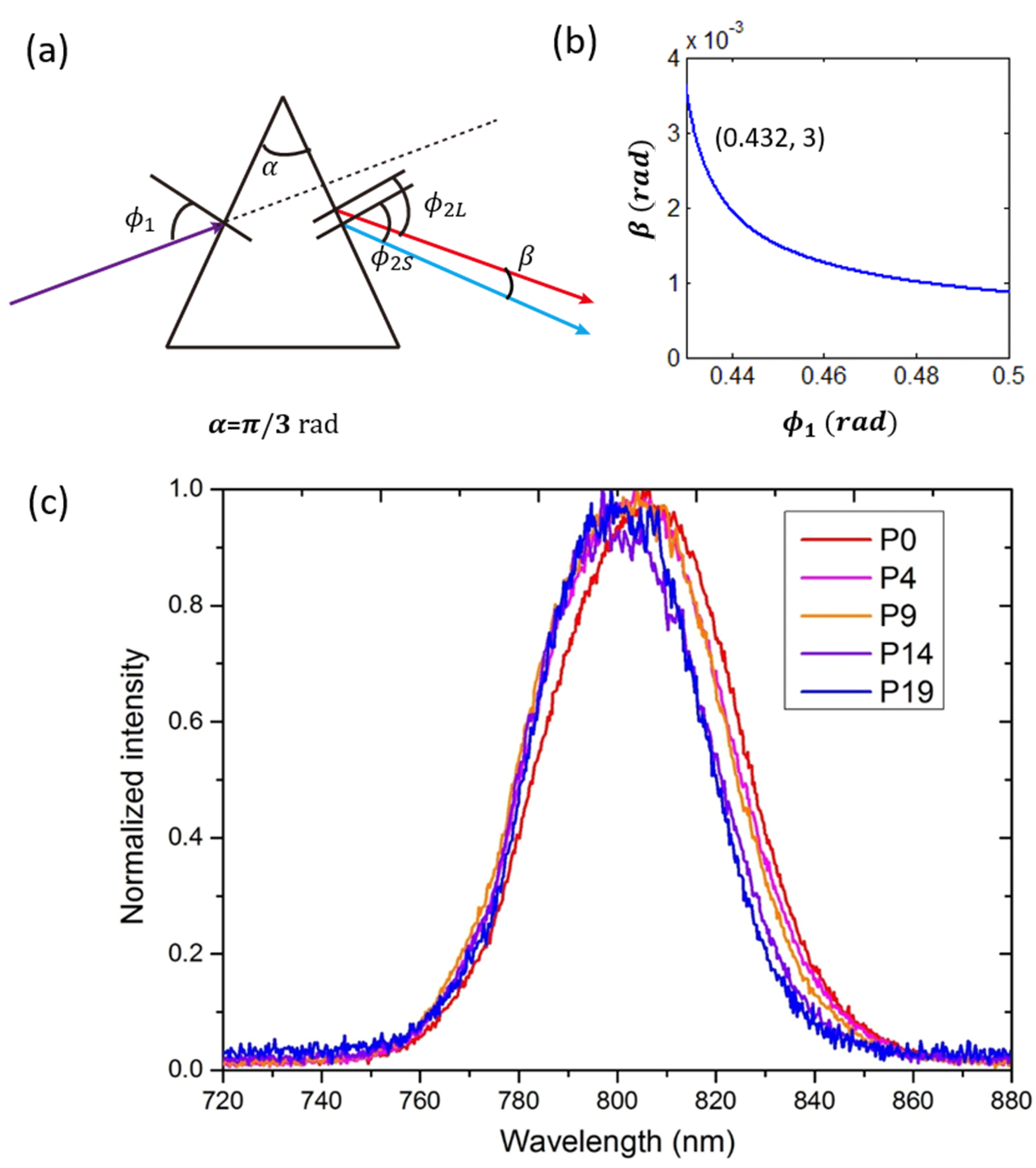
Figure 6. (a) Scheme of prism dispersion; (b) the relationship between the incident angle
![]() $\emptyset _{1}$
and the dispersion angle of pulses with
$\emptyset _{1}$
and the dispersion angle of pulses with
![]() $\unicode[STIX]{x1D706}_{NS}=795$
nm and
$\unicode[STIX]{x1D706}_{NS}=795$
nm and
![]() $\unicode[STIX]{x1D706}_{NL}=815$
nm; (c) spectra of compensated SD signal.
$\unicode[STIX]{x1D706}_{NL}=815$
nm; (c) spectra of compensated SD signal.
The angular dispersion compensated
![]() $SD_{+1}$
propagates about 1500 mm, and is expanded to about 20 mm in the horizontal direction. The spectra of
$SD_{+1}$
propagates about 1500 mm, and is expanded to about 20 mm in the horizontal direction. The spectra of
![]() $SD_{+1}$
at five different positions with 5 mm apart are shown in Figure 6(c).
$SD_{+1}$
at five different positions with 5 mm apart are shown in Figure 6(c).
As can be seen in Figure 6(c), the spectra of compensated
![]() $SD_{+1}$
at five different positions show a good coincidence. While, residual angular dispersion still exists, and it is clear that the compensation for the shorter wavelengths appears better than that for the longer wavelengths, we think this is the residual high-order angular dispersion as the center wavelengths vary nonlinearly relative to the five positions of equal interval.
$SD_{+1}$
at five different positions show a good coincidence. While, residual angular dispersion still exists, and it is clear that the compensation for the shorter wavelengths appears better than that for the longer wavelengths, we think this is the residual high-order angular dispersion as the center wavelengths vary nonlinearly relative to the five positions of equal interval.
4 Conclusion
In conclusion, temporal contrast enhancement by the SD process in a bulk Kerr medium possesses a few advantages compared to many other pulse cleaning techniques. The SD signals are spatially separated from the incident beams without the use of any polarization discrimination devices. It can also achieve a high energy SD signal output with a cylindrical mirror focusing on the incident beams even with low energy-conversion efficiency. The temporal contrast of the
![]() $SD_{+1}$
signal is the cube of the temporal contrast of the incident pulse,
$SD_{+1}$
signal is the cube of the temporal contrast of the incident pulse,
![]() $C_{SD+1}\approx C_{in}^{3}$
in theory, which indicates a great potential of temporal contrast enhancement by the SD process.
$C_{SD+1}\approx C_{in}^{3}$
in theory, which indicates a great potential of temporal contrast enhancement by the SD process.
In this study, a temporal contrast enhancement equipment based on SD effect with two cylindrical convex lenses is built. As high as
![]() $780~\unicode[STIX]{x03BC}\text{J}$
first-order SD signal at 800 nm with contrast of
$780~\unicode[STIX]{x03BC}\text{J}$
first-order SD signal at 800 nm with contrast of
![]() $10^{12}$
is generated with about five orders of magnitude improvement. Wings around the main pulse in
$10^{12}$
is generated with about five orders of magnitude improvement. Wings around the main pulse in
![]() $\pm 1~\text{ps}$
are cleaned with a contrast improvement of about
$\pm 1~\text{ps}$
are cleaned with a contrast improvement of about
![]() $10^{7}$
, which verifies the pulse cleaning ability of SD process. The cause of angular dispersion generation of the SD signals is also explored, and the angular dispersion is compensated with a single prism. It is expected to extend the SD process as an effective pulse cleaning method for high power laser at 1053 nm with a narrow spectral bandwidth and hundreds of femtosecond pulse duration.
$10^{7}$
, which verifies the pulse cleaning ability of SD process. The cause of angular dispersion generation of the SD signals is also explored, and the angular dispersion is compensated with a single prism. It is expected to extend the SD process as an effective pulse cleaning method for high power laser at 1053 nm with a narrow spectral bandwidth and hundreds of femtosecond pulse duration.
Acknowledgements
The authors would like to thank Wei Chu and Ziting Li for the support of laser sources, and Yi Xu for his help on temporal contrast measurement. This work is supported by the National Natural Science Foundation of China (NSFC) (Nos. 11274327, 61521093, and 61527821), the Instrument Developing Project of the Chinese Academy of Sciences (No. YZ201538), and the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB16).