Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T21:20:32.913Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE FAMILY OF DIOPHANTINE TRIPLES {k − 1, k + 1, 16k 3 − 4k}

Published online by Cambridge University Press:  09 August 2007

YANN BUGEAUD ,
ANDREJ DUJELLA  and
MAURICE MIGNOTTE
YANN BUGEAUD
Affiliation:
Université Louis Pasteur, U. F. R. de Mathématiques, 7, rue René Descartes, 67084 Strasbourg, France e-mail: [email protected]
ANDREJ DUJELLA
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia e-mail: [email protected]
MAURICE MIGNOTTE
Affiliation:
Université Louis Pasteur, U. F. R. de Mathématiques, 7, rue René Descartes, 67084 Strasbourg, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

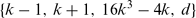It is proven that if k ≥ 2 is an integer and d is a positive integer such that the product of any two distinct elements of the set increased by 1 is a perfect square, then d = 4k or d = 64k 5−48k 3+8k. Together with a recent result of Fujita, this shows that all Diophantine quadruples of the form {k − 1, k + 1, c, d} are regular.

Keywords

11D0911D2511J8611Y50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 2 , May 2007 , pp. 333 - 344
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1. Baker, A. and Davenport, H., The equations 3x 2−2=y 2 and 8x 2−7=z 2 , Quart. J. Math. Oxford Ser. (2) 20 (1969), 129–137.CrossRefGoogle Scholar
2. Baker, A. and Wüstholz, G., Logarithmic forms and group varieties, J. Reine Angew. Math. 442 (1993), 19–62.Google Scholar
3. Bennett, M. A., On the number of solutions of simultaneous Pell equations, J. Reine Angew. Math. 498 (1998), 173–199.CrossRefGoogle Scholar
4. Dickson, L. E., History of the theory of numbers, Vol. 2, Diophantinc analysis (Chelsea, New York, 1966), 513–520.Google Scholar
5. Diophantus of Alexandria, Arithmetics and the book of polygonal numbers (Bashmakova, I. G., Ed.), Nauka, Moscow, 1974 (in Russian), 103–104, 232.Google Scholar
6. Dujella, A., The problem of the extension of a parametric family of Diophantine triples, Publ. Math. Debrecen 51 (1997), 311–322.CrossRefGoogle Scholar
7. Dujella, A., An absolute bound for the size of Diophantine m-tuples, J. Number Theory 89 (2001), 126–150.CrossRefGoogle Scholar
8. Dujella, A., There are only finitely many Diophantine quintuples, J. Reine Angew. Math. 566 (2004), 183–214.Google Scholar
9. Dujella, A. and Pethö, A., A generalization of a theorem of Baker and Davenport, Quart. J. Math. Oxford Ser. (2) 49 (1998), 291–306.CrossRefGoogle Scholar
10. Gibbs, P., Some rational Diophantine sextuples, Glas. Mat. Ser. III 41 (2006), 195–203.CrossRefGoogle Scholar
11. Gibbs, P., A generalised Stern-Brocot tree from regular Diophantine quadruples, preprint, math.NT/9903035.Google Scholar
12. Fujita, Y., The extensibility of Diophantine pairs k−1, k+1, preprint.Google Scholar
13. Heath, T. L., Diophantus of Alexandria: a study in the history of Greek algebra. Second edition. With a supplement containing an account of Fermat's theorems and problems connected with Diophantine analysis and some solutions of Diophantine problems by Euler (Powell's Bookstore, Chicago and Martino Publishing, Mansfield Center, 2003), 177–181.Google Scholar
14. Matveev, E. M., An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers. II (Russian), Izv. Ross. Akad. Nauk Ser. Mat. 64 (2000), no. 6, 125–180.Google Scholar
15. Mignotte, M., A kit on linear forms in three logarithms, preprint.Google Scholar