Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T07:35:25.210Z Has data issue: false hasContentIssue false
  • English
  • Français

On coefficient fields

Published online by Cambridge University Press:  18 May 2009

A. Geddes
A. Geddes
Affiliation:
The University Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Q be a complete local ring which has the same characteristic as its residue field P, and, for the present, let us denote by A the image of a subset A of Q under the natural homomorphism of Q onto P. Then a subfield F of Q is called a coefficient field if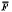 = P. It has been shown in [2] and in [3] that a complete equicharacteristic local ring, such as the above, always possesses at least one coefficient field; this is the embedding theorem for the equicharacteristic case.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 1 , December 1958 , pp. 42 - 48
Copyright
Copyright © Glasgow Mathematical Journal Trust 1958

References

1.Chevalley, C., On the theory of local rings, Ann. Math., 44 (1943), 690–708.CrossRefGoogle Scholar
2.Cohen, I. S., On the structure and ideal theory of complete local rings, Trans. Amer. Math. Soc., 59 (1946), 54–106.CrossRefGoogle Scholar
3.Geddes, A., A short proof of the existence of coefficient fields for complete equicharacteristic local rings, J. London Math. Soc., 29 (1954), 334–341.CrossRefGoogle Scholar
4.Geddes, A., On the embedding theorems for complete local rings, Proc London Math. Soc.(3), 6 (1956), 343–354.CrossRefGoogle Scholar
5.Zariski, O. and Samuel, P., Commutative Algebra (Volume 1) (Princeton, 1958).Google Scholar