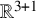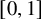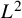1 Introduction
1.1 Motivation and review of the classical results
The study of nonlinear wave equations, nonlinear Klein-Gordon equations and their coupled systems has been an active area of research for decades, and the question ‘what kind of quadratic nonlinearities lead to global-in-time solutions?’ has attracted special attention from researchers. In addition to the mathematical interest and challenges, such studies are also motivated by the Einstein equations, the Einstein-Klein-Gordon equations, the Yang-Mills equations, the electroweak standard model and many other important models from mathematical physics. Recall that, on the one hand, wave equations in ![]() $\mathbb {R}^{3+1}$ with null form nonlinearities were proved to admit global-in-time solutions independently by Klainerman [Reference Klainerman14] and Christodoulou [Reference Christodoulou2] (and Klainerman identified the class of null forms); see also the generalizations of null condition to the weak null condition in [Reference Lindblad and Rodnianski19, Reference Lindblad and Rodnianski20] and to the non-resonant condition in [Reference Pusateri and Shatah22], for instance. On the other hand, it was shown by Klainerman [Reference Klainerman12] and Shatah [Reference Shatah23] that Klein-Gordon equations with general quadratic nonlinearities in
$\mathbb {R}^{3+1}$ with null form nonlinearities were proved to admit global-in-time solutions independently by Klainerman [Reference Klainerman14] and Christodoulou [Reference Christodoulou2] (and Klainerman identified the class of null forms); see also the generalizations of null condition to the weak null condition in [Reference Lindblad and Rodnianski19, Reference Lindblad and Rodnianski20] and to the non-resonant condition in [Reference Pusateri and Shatah22], for instance. On the other hand, it was shown by Klainerman [Reference Klainerman12] and Shatah [Reference Shatah23] that Klein-Gordon equations with general quadratic nonlinearities in ![]() $\mathbb {R}^{3+1}$ admit small solutions. In addition, the global well-posedness results for different types of coupled wave and Klein-Gordon systems, with or without physical models behind, were obtained; see, for instance, [Reference Bachelot1, Reference Dong and Wyatt6, Reference Dong, LeFloch and Wyatt5, Reference Georgiev7, Reference Ionescu and Pausader9, Reference Ionescu and Pausader10, Reference Katayama11, Reference Klainerman, Wang and Yang15, Reference LeFloch and Ma16, Reference LeFloch and Ma17, Reference LeFloch and Ma18, Reference Ozawa, Tsutaya and Tsutsumi21, Reference Wang27].
$\mathbb {R}^{3+1}$ admit small solutions. In addition, the global well-posedness results for different types of coupled wave and Klein-Gordon systems, with or without physical models behind, were obtained; see, for instance, [Reference Bachelot1, Reference Dong and Wyatt6, Reference Dong, LeFloch and Wyatt5, Reference Georgiev7, Reference Ionescu and Pausader9, Reference Ionescu and Pausader10, Reference Katayama11, Reference Klainerman, Wang and Yang15, Reference LeFloch and Ma16, Reference LeFloch and Ma17, Reference LeFloch and Ma18, Reference Ozawa, Tsutaya and Tsutsumi21, Reference Wang27].
It is well known that (linear) Klein-Gordon components decay ![]() $t^{-1/2}$ faster than the (linear) wave components in
$t^{-1/2}$ faster than the (linear) wave components in ![]() $\mathbb {R}^{n+1}$ (
$\mathbb {R}^{n+1}$ (![]() $n \geq 1$) and that the presence of the mass term allows one to control the
$n \geq 1$) and that the presence of the mass term allows one to control the ![]() $L^2$–type energy of the Klein-Gordon components by their natural energy. Both of these make it less difficult to study nonlinear Klein-Gordon equations in
$L^2$–type energy of the Klein-Gordon components by their natural energy. Both of these make it less difficult to study nonlinear Klein-Gordon equations in ![]() $\mathbb {R}^{3+1}$. When it comes to the study of nonlinear wave equations, we can utilise the scaling vector field, which makes it easy to apply the Klainerman-Sobolev inequality, and we can rely on the conformal energy estimates to obtain
$\mathbb {R}^{3+1}$. When it comes to the study of nonlinear wave equations, we can utilise the scaling vector field, which makes it easy to apply the Klainerman-Sobolev inequality, and we can rely on the conformal energy estimates to obtain ![]() $L^2$–type energy estimates for wave components (with no derivatives). Thus, we can see from the simple comparisons above that different features help to study pure wave equations and pure Klein-Gordon equations.
$L^2$–type energy estimates for wave components (with no derivatives). Thus, we can see from the simple comparisons above that different features help to study pure wave equations and pure Klein-Gordon equations.
Concerning the fact that Klein-Gordon equations become wave equations when the masses are set to be 0, a natural interesting question is that for Klein-Gordon equations with varying mass in ![]() $[0, 1]$, what kind of quadratic nonlinearities can ensure small data global existence results that are uniform in terms of the varying mass parameter? Our primary goal is to prove that all kinds of null nonlinearities can uniformly guarantee global existence results for systems of Klein-Gordon equations with mass varying in
$[0, 1]$, what kind of quadratic nonlinearities can ensure small data global existence results that are uniform in terms of the varying mass parameter? Our primary goal is to prove that all kinds of null nonlinearities can uniformly guarantee global existence results for systems of Klein-Gordon equations with mass varying in ![]() $[0, 1]$. Such results are known to be valid at the end points
$[0, 1]$. Such results are known to be valid at the end points ![]() $0, 1$, which correspond to wave equations and Klein-Gordon equations with fixed mass, respectively. But more is involved if one wants to get global existence results uniform in terms of the mass parameter in
$0, 1$, which correspond to wave equations and Klein-Gordon equations with fixed mass, respectively. But more is involved if one wants to get global existence results uniform in terms of the mass parameter in ![]() $[0, 1]$, because, for instance, we cannot use the scaling vector field, cannot obtain mass-independent
$[0, 1]$, because, for instance, we cannot use the scaling vector field, cannot obtain mass-independent ![]() $L^2$–type estimates by the mass term or by the conformal energy estimates, and so on. The main difficulties arise when the mass is close to 0, which is why we refer to this problem as the zero mass problem of the Klein-Gordon equations.
$L^2$–type estimates by the mass term or by the conformal energy estimates, and so on. The main difficulties arise when the mass is close to 0, which is why we refer to this problem as the zero mass problem of the Klein-Gordon equations.
In addition, the study of the Klein-Gordon equations with varying mass (especially when the mass goes to 0) is also motivated by the study of mathematical physics. We briefly recall in [Reference Dong, LeFloch and Wyatt5] that when studying the electroweak standard model, there appear several Klein-Gordon equations with different masses, and physical experiments have verified that some of the masses are extremely small (close to 0 but still positive) compared to others. Thus it is important to obtain results that are uniform in terms of the small masses for Klein-Gordon equations. Since the cases of ![]() $m=0, 1$ have been well studied, we will only focus on Klein-Gordon equations with one single mass
$m=0, 1$ have been well studied, we will only focus on Klein-Gordon equations with one single mass ![]() $m \in [0, 1]$ to capture the most interesting feature instead of coupling with Klein-Gordon equations with masses
$m \in [0, 1]$ to capture the most interesting feature instead of coupling with Klein-Gordon equations with masses ![]() $0, 1$.
$0, 1$.
1.2 Model of interest
We will consider the following system of coupled Klein-Gordon equations with varying mass ![]() $m \in [0, 1]$:
$m \in [0, 1]$:
with initial data prescribed on ![]() $t = t_0 = 2$
$t = t_0 = 2$
In the above, ![]() $\Box = \eta ^{\alpha \beta } {\partial }_{\alpha \beta }$ is the wave operator, where
$\Box = \eta ^{\alpha \beta } {\partial }_{\alpha \beta }$ is the wave operator, where ![]() $\eta = \text {diag}(-1, 1, 1, 1)$ is the metric of the spacetime, and the Einstein summation convention is adopted. We note that
$\eta = \text {diag}(-1, 1, 1, 1)$ is the metric of the spacetime, and the Einstein summation convention is adopted. We note that ![]() $Q_0 (v_j, v_k) = {\partial }_\alpha v_j {\partial }^\alpha v_k$ and
$Q_0 (v_j, v_k) = {\partial }_\alpha v_j {\partial }^\alpha v_k$ and ![]() $Q_{\alpha \beta } (v_j, v_k) = {\partial }_\alpha v_j {\partial }_\beta v_k - {\partial }_\alpha v_k {\partial }_\beta v_j$ are classical null forms of Klainerman. The indices
$Q_{\alpha \beta } (v_j, v_k) = {\partial }_\alpha v_j {\partial }_\beta v_k - {\partial }_\alpha v_k {\partial }_\beta v_j$ are classical null forms of Klainerman. The indices ![]() $i, j, k \in \{1, \cdots , N_0 \}$ with
$i, j, k \in \{1, \cdots , N_0 \}$ with ![]() $N_0$ the number of equations (also the number of unknowns), and we use
$N_0$ the number of equations (also the number of unknowns), and we use ![]() $a, b, c, \cdots \in \{1, 2, 3\}$ and
$a, b, c, \cdots \in \{1, 2, 3\}$ and ![]() $\alpha , \beta , \gamma , \cdots \{0, 1, 2, 3\}$ to denote the space indices and the spacetime indices, respectively. Throughout the paper, we will also use
$\alpha , \beta , \gamma , \cdots \{0, 1, 2, 3\}$ to denote the space indices and the spacetime indices, respectively. Throughout the paper, we will also use ![]() $A \lesssim B$ to indicate
$A \lesssim B$ to indicate ![]() $A \leq C B$, with C a generic constant (independent of the mass parameter m).
$A \leq C B$, with C a generic constant (independent of the mass parameter m).
At the end points of ![]() $m = 0$ and
$m = 0$ and ![]() $m = 1$, the small data global existence result (as well as other properties of the solution) for the system in equations (1.1)–(1.2) is well known, and the proofs are conducted depending on the different features of the pure wave equations and the pure Klein-Gordon equations. Here we want to establish the global existence result and explore the properties of the solution for the system in equation (1.1), which are uniform in terms of the mass parameter
$m = 1$, the small data global existence result (as well as other properties of the solution) for the system in equations (1.1)–(1.2) is well known, and the proofs are conducted depending on the different features of the pure wave equations and the pure Klein-Gordon equations. Here we want to establish the global existence result and explore the properties of the solution for the system in equation (1.1), which are uniform in terms of the mass parameter ![]() $m \in [0, 1]$, by which we mean the smallness of the initial data is independent of m. In addition, we derive the unified pointwise decay result for the equations, by which we mean the pointwise decay result unifies the wave and the Klein-Gordon equations with explicit dependence on the mass parameter m. In addition, it is also interesting to show that the solution to equation (1.1) converges to the corresponding wave system when
$m \in [0, 1]$, by which we mean the smallness of the initial data is independent of m. In addition, we derive the unified pointwise decay result for the equations, by which we mean the pointwise decay result unifies the wave and the Klein-Gordon equations with explicit dependence on the mass parameter m. In addition, it is also interesting to show that the solution to equation (1.1) converges to the corresponding wave system when ![]() $m \to 0$. Since some features of the pure wave equations or the pure Klein-Gordon equations cannot be relied on when obtaining the uniform result, the analysis of the proof is more subtle and requires new insights.
$m \to 0$. Since some features of the pure wave equations or the pure Klein-Gordon equations cannot be relied on when obtaining the uniform result, the analysis of the proof is more subtle and requires new insights.
1.3 Difficulties and new observations
When studying the Klein-Gordon equations, the most well-known difficulty is that one cannot use the scaling vector field because the scaling vector field does not commute with the Klein-Gordon operators. However, more difficulties arise in studying the Klein-Gordon system with possibly vanishing mass.
First, in order to apply Sobolev–type inequalities to obtain pointwise decay results for the Klein-Gordon components ![]() $v = (v_i)$ or to estimate the null forms, we need to bound the
$v = (v_i)$ or to estimate the null forms, we need to bound the ![]() $L^2$–type norm for
$L^2$–type norm for ![]() $v_i$, which is supposed to be mass-independent, and this is the most difficult part. On the one hand, the presence of the mass term in the Klein-Gordon equation does not seem to help obtain the
$v_i$, which is supposed to be mass-independent, and this is the most difficult part. On the one hand, the presence of the mass term in the Klein-Gordon equation does not seem to help obtain the ![]() $L^2$–type energy estimate. That is because what we can get from the mass term is only
$L^2$–type energy estimate. That is because what we can get from the mass term is only
Footnote 1which is mass-dependent, and very unfortunately, the bound for ![]() $\| v \|_{L^2}$ blows up when m goes to 0; and in the above, B represents some bound from the energy estimates. On the other hand, the conformal energy estimates allow one to get the
$\| v \|_{L^2}$ blows up when m goes to 0; and in the above, B represents some bound from the energy estimates. On the other hand, the conformal energy estimates allow one to get the ![]() $L^2$–type estimates for wave components (i.e., the cases of
$L^2$–type estimates for wave components (i.e., the cases of ![]() $m = 0$), but they can no longer be applied due to the presence of the mass term, which means we cannot obtain
$m = 0$), but they can no longer be applied due to the presence of the mass term, which means we cannot obtain ![]() $L^2$–type estimates for
$L^2$–type estimates for ![]() $v_i$ using the conformal energy. Second, the solution to the system in equation (1.1) does not decay sufficiently fast. In general, we can expect solutions to Klein-Gordon equations with fixed mass to decay like
$v_i$ using the conformal energy. Second, the solution to the system in equation (1.1) does not decay sufficiently fast. In general, we can expect solutions to Klein-Gordon equations with fixed mass to decay like ![]() $t^{-3/2}$ in
$t^{-3/2}$ in ![]() $\mathbb {R}^{3+1}$, but due to the possibly vanishing mass
$\mathbb {R}^{3+1}$, but due to the possibly vanishing mass ![]() $m \in [0, 1]$, the best we can expect for the Klein-Gordon components
$m \in [0, 1]$, the best we can expect for the Klein-Gordon components ![]() $v_i$ is the (mass-independent) wave decay
$v_i$ is the (mass-independent) wave decay
and the (mass-dependent) Klein-Gordon decay
In addition, the null form of the type ![]() ${\partial }^\alpha v_j {\partial }_\alpha v_k$ does not seem to decay sufficiently fast. It is not consistent with the Klein-Gordon equations since we lack the scaling vector field to gain a good factor of
${\partial }^\alpha v_j {\partial }_\alpha v_k$ does not seem to decay sufficiently fast. It is not consistent with the Klein-Gordon equations since we lack the scaling vector field to gain a good factor of ![]() $t^{-1}$ from
$t^{-1}$ from ![]() ${\partial }^\alpha v_j {\partial }_\alpha v_k$. Last but not least, there are some difficulties in gaining the factor
${\partial }^\alpha v_j {\partial }_\alpha v_k$. Last but not least, there are some difficulties in gaining the factor ![]() $t^{-1}$ from the null forms
$t^{-1}$ from the null forms ![]() $Q_0 (v_j, v_k), Q_{\alpha \beta }(v_j, v_k)$ in the highest-order energy estimate, which again is due to the lack of the conformal energy estimate.
$Q_0 (v_j, v_k), Q_{\alpha \beta }(v_j, v_k)$ in the highest-order energy estimate, which again is due to the lack of the conformal energy estimate.
In order to tackle the problems caused by the presence of the possibly vanishing mass term, we will rely on the following key observations and insights. First, we will use the hyperboloidal foliation of the spacetime to prove the (uniform) global existence result for the system in equation (1.1), which is developed by Klainerman [Reference Klainerman12], Hormander [Reference Hörmander8], LeFloch-Ma [Reference LeFloch and Ma16], and so forth. We will take advantage of the fact that the null forms (![]() $Q_0, Q_{\alpha \beta }$) can be decomposed as sums of products of good components in the hyperboloidal foliation setting (see Lemma 2.4); this is true even for the highest-order energy estimate. As a consequence, we are able to obtain the mass-dependent pointwise decay result
$Q_0, Q_{\alpha \beta }$) can be decomposed as sums of products of good components in the hyperboloidal foliation setting (see Lemma 2.4); this is true even for the highest-order energy estimate. As a consequence, we are able to obtain the mass-dependent pointwise decay result
Next, we will move to the usual flat foliation of the spacetime to show the unified pointwise decay result, which is the most difficult part. To achieve this, we will obtain the mass-independent ![]() $L^2$–type norm estimates for the solution
$L^2$–type norm estimates for the solution ![]() $v = (v_i)$ by using tricks from the Fourier analysis. To be more precise, we write the Klein-Gordon equation in the Fourier space and solve the corresponding ordinary differential equation to get the solution in the Fourier space, and then obtain the mass-independent
$v = (v_i)$ by using tricks from the Fourier analysis. To be more precise, we write the Klein-Gordon equation in the Fourier space and solve the corresponding ordinary differential equation to get the solution in the Fourier space, and then obtain the mass-independent ![]() $L^2$–type norm estimates for the solution
$L^2$–type norm estimates for the solution ![]() $v = (v_i)$ (see Proposition 3.1). However, according to Proposition 3.1, in order to get sufficiently good
$v = (v_i)$ (see Proposition 3.1). However, according to Proposition 3.1, in order to get sufficiently good ![]() $L^2$–type estimates for the solution, we need to gain the extra factor
$L^2$–type estimates for the solution, we need to gain the extra factor ![]() $t^{-1}$ from the null nonlinearities. For the null forms of type
$t^{-1}$ from the null nonlinearities. For the null forms of type ![]() $Q_{\alpha \beta }$, we easily have
$Q_{\alpha \beta }$, we easily have
and for the higher-order case, the following observation (from [Reference Katayama11]) helps
thanks to the hidden divergence form of the null nonlinearities ![]() $Q_{\alpha \beta }$. For the null forms of type
$Q_{\alpha \beta }$. For the null forms of type ![]() $Q_0$, at first glance, it does not seem to be possible to gain the factor
$Q_0$, at first glance, it does not seem to be possible to gain the factor ![]() $t^{-1}$ from the null form
$t^{-1}$ from the null form ![]() $Q_0$ because we do not have good control over the scaling vector field. But we observe that a nonlinear transformation will help, which transforms the quadratic term
$Q_0$ because we do not have good control over the scaling vector field. But we observe that a nonlinear transformation will help, which transforms the quadratic term ![]() $Q_0$ to the sum of cubic terms and quadratic terms with a good factor
$Q_0$ to the sum of cubic terms and quadratic terms with a good factor ![]() $m^2$ in front. These observations allow us to obtain the mass-independent
$m^2$ in front. These observations allow us to obtain the mass-independent ![]() $L^2$–type estimates, and hence the mass-independent pointwise decay result for the solution
$L^2$–type estimates, and hence the mass-independent pointwise decay result for the solution
can be obtained with the aid of the Klainerman-Sobolev inequality in Proposition 2.6. More details follow. We will divide the solution into several parts and analyse each part according to its features. For the parts where we can gain ![]() $t^{-1}$ factor from the null form or the nonlinearities are cubic, Proposition 3.1 will be sufficient to obtain the mass-independent pointwise decay. For the part with quadratic nonlinearities with the good factor
$t^{-1}$ factor from the null form or the nonlinearities are cubic, Proposition 3.1 will be sufficient to obtain the mass-independent pointwise decay. For the part with quadratic nonlinearities with the good factor ![]() $m^2$, we will carefully study the m-dependent relation of the norms of the nonlinearities and try to gain the factor m to cancel the one appearing in the energy.
$m^2$, we will carefully study the m-dependent relation of the norms of the nonlinearities and try to gain the factor m to cancel the one appearing in the energy.
1.4 Main theorem
Now we provide the statement of the main result.
Theorem 1.1. Consider the system of Klein-Gordon equations (1.1) with mass ![]() $m \in [0, 1]$, and let
$m \in [0, 1]$, and let ![]() $N \geq 6$ be an integer. There exists small
$N \geq 6$ be an integer. There exists small ![]() ${\epsilon }_0> 0$, which is independent of the mass parameter m, such that for all
${\epsilon }_0> 0$, which is independent of the mass parameter m, such that for all ![]() ${\epsilon } < {\epsilon }_0$ and all compactly supported initial data that are small in the sense that
${\epsilon } < {\epsilon }_0$ and all compactly supported initial data that are small in the sense that
then the Cauchy problem in equations (1.1)–(1.2) admits a global-in-time solution ![]() $v = (v_i)$. In addition, the unified decay of the solution is obtained
$v = (v_i)$. In addition, the unified decay of the solution is obtained
In the proof of Theorem 1.1, we will always assume ![]() $m \in (0, 1]$ unless specified since the result for the case of
$m \in (0, 1]$ unless specified since the result for the case of ![]() $m = 0$ is well-known and classical. We will also assume the initial data
$m = 0$ is well-known and classical. We will also assume the initial data ![]() $(v_{i0}, v_{i1})$ are spatially supported in the unit ball
$(v_{i0}, v_{i1})$ are spatially supported in the unit ball ![]() $\{(x, t) : t = t_0 = 2, |x| \leq 1 \}$, but the results in the theorem still hold for all of the initial data prescribed at any
$\{(x, t) : t = t_0 = 2, |x| \leq 1 \}$, but the results in the theorem still hold for all of the initial data prescribed at any ![]() $t=constant$ with compact support; see the remark in [Reference Dong and Wyatt6] that is below the main theorem there. We note that the compactness assumption implies
$t=constant$ with compact support; see the remark in [Reference Dong and Wyatt6] that is below the main theorem there. We note that the compactness assumption implies
and this will be used when applying Proposition 3.1.
It can be seen from Theorem 1.1 that the global existence result and the pointwise decay result are both consistent with the cases of ![]() $m = 0$ and
$m = 0$ and ![]() $m = 1$, which are the usual wave equations and the usual Klein-Gordon equations (with fixed mass). It is worth mentioning that the unified decay result in equation (1.4) shows that the solution decays more like a wave component (with no m dependence) as
$m = 1$, which are the usual wave equations and the usual Klein-Gordon equations (with fixed mass). It is worth mentioning that the unified decay result in equation (1.4) shows that the solution decays more like a wave component (with no m dependence) as ![]() $t^{-1}$ in the time range
$t^{-1}$ in the time range ![]() $t \in [t_0, m^{-2})$, while it decays more like a Klein-Gordon component (with m dependence) as
$t \in [t_0, m^{-2})$, while it decays more like a Klein-Gordon component (with m dependence) as ![]() $m^{-1} t^{-3/2}$ in the rest of the time range (if non-empty). In addition to the results contained in Theorem 1.1, we have the following convergence result, which tells us that the solution to the system in equation (1.1) converges to the solution to the corresponding wave system (i.e., the system in equation (1.1) with
$m^{-1} t^{-3/2}$ in the rest of the time range (if non-empty). In addition to the results contained in Theorem 1.1, we have the following convergence result, which tells us that the solution to the system in equation (1.1) converges to the solution to the corresponding wave system (i.e., the system in equation (1.1) with ![]() $m=0$) in a certain sense. Let
$m=0$) in a certain sense. Let
denote the solution to the system in equation (1.1) with mass m, and we can now demonstrate the convergence theorem.
Theorem 1.2. Consider the system in equation (1.1), and let the same assumptions in Theorem 1.1 hold. Then the solution to the system in equation (1.1) with mass m converges to the system in equation (1.1) with ![]() $m = 0$, in the sense that (with
$m = 0$, in the sense that (with ![]() $0 < \delta \ll 1$)
$0 < \delta \ll 1$)
We note that Theorem 1.2 indicates that the solution ![]() $v^{(m)}$ tends to
$v^{(m)}$ tends to ![]() $v^{(0)}$ at the rate
$v^{(0)}$ at the rate ![]() $m^2$ when
$m^2$ when ![]() $m \to 0$ on each fixed slice
$m \to 0$ on each fixed slice ![]() $t = constant$, but the bounds for the energy of the difference
$t = constant$, but the bounds for the energy of the difference ![]() $v^{(m)} - v^{(0)}$ blow up as
$v^{(m)} - v^{(0)}$ blow up as ![]() $t \to +\infty $ for each fixed m.
$t \to +\infty $ for each fixed m.
The study of the zero mass problem of the Klein-Gordon equations is a new subject. We recall that such studies have appeared in earlier work [Reference Dong, LeFloch and Wyatt5, Reference Dong3], where the zero mass problem for Dirac equations (we note that Dirac equations can be transformed into Klein-Gordon equations) and Klein-Gordon equations with divergence form nonlinearities were investigated. In this paper, we extend the earlier work to be able to treat quadratic nonlinearities satisfying the null condition, which is a big step forward. It is also natural to deal with null forms as they frequently appear in the field of wave and Klein-Gordon equations. Of great mathematical interest, the zero mass problem for the Klein-Gordon equations with more types of nonlinearities, as well as in the low dimension cases, is to be studied, which also seems very promising and challenging.
1.5 Further discussions
The goal of this part is to discuss one way to show global existence for nonlinear Klein-Gordon equations with some restricted bounded large data. For general bounded large data, our method does not apply.
For simplicity, we consider the Klein-Gordon equation with ![]() $m \in (0, 1]$ (note we exclude
$m \in (0, 1]$ (note we exclude ![]() $m=0$ with no harm)
$m=0$ with no harm)
 $$ \begin{align} \begin{aligned} &-\Box u + m^2 u = {\partial}_\alpha u {\partial}^\alpha u, \\ &\big(u, {\partial}_t u \big)(t=0) = (u_0, u_1) = (u_0, 0). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &-\Box u + m^2 u = {\partial}_\alpha u {\partial}^\alpha u, \\ &\big(u, {\partial}_t u \big)(t=0) = (u_0, u_1) = (u_0, 0). \end{aligned} \end{align} $$From Theorem 1.1, we know there exists ![]() ${\epsilon }_0$ independent of m, such that for all compactly supported initial data satisfying the smallness condition
${\epsilon }_0$ independent of m, such that for all compactly supported initial data satisfying the smallness condition
the Cauchy problem in equation (1.6) admits a global solution with pointwise decay
We introduce the new spacetime variables
and define the function
A simple calculation shows that ![]() $U(T, X)$ solves the nonlinear Klein-Gordon equation with fixed mass
$U(T, X)$ solves the nonlinear Klein-Gordon equation with fixed mass ![]() $1$, which reads
$1$, which reads
 $$ \begin{align} \begin{aligned} &{\partial}_T {\partial}_T U(T, X) - \sum_a {\partial}_{X^a} {\partial}_{X^a} U(T, X) + U(T, X) = -\big({\partial}_T U(T, X) \big)^2 + \sum_a \big( {\partial}_{X^a} U(T, X) \big)^2,\\ &\big( U(T, X), {\partial}_T U(T, X) \big)(T=0) = (U_0 (X), 0), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{\partial}_T {\partial}_T U(T, X) - \sum_a {\partial}_{X^a} {\partial}_{X^a} U(T, X) + U(T, X) = -\big({\partial}_T U(T, X) \big)^2 + \sum_a \big( {\partial}_{X^a} U(T, X) \big)^2,\\ &\big( U(T, X), {\partial}_T U(T, X) \big)(T=0) = (U_0 (X), 0), \end{aligned} \end{align} $$in which
We observe that
Clearly, for any chosen non-zero small initial data ![]() $(u_0, 0)$ for equation (1.6), we can always pick
$(u_0, 0)$ for equation (1.6), we can always pick ![]() $m \in (0, 1]$ sufficiently small so that the initial data for equation (1.7) is large: that is, satisfying
$m \in (0, 1]$ sufficiently small so that the initial data for equation (1.7) is large: that is, satisfying
for any given large constant ![]() $C_L> 1$. This means the nonlinear Klein-Gordon equation (1.7) with fixed mass
$C_L> 1$. This means the nonlinear Klein-Gordon equation (1.7) with fixed mass ![]() $1$ admits a global solution even if the size of the initial data is large (but restricted).
$1$ admits a global solution even if the size of the initial data is large (but restricted).
1.6 Outline
The rest of this paper is organised as follows: In Section 2, we revisit some notations, Sobolev–type inequalities and basic results on the Klein-Gordon equations. Next, we provide the key result of obtaining the mass-independent ![]() $L^2$ norm estimates for solutions to the Klein-Gordon equations with possibly vanishing masses in Section 3. Then we prove the global existence result in Section 4. Finally, the proof for the mass-independent decay result and the proof for the convergence result are illustrated in Section 5 and Section 6, respectively.
$L^2$ norm estimates for solutions to the Klein-Gordon equations with possibly vanishing masses in Section 3. Then we prove the global existence result in Section 4. Finally, the proof for the mass-independent decay result and the proof for the convergence result are illustrated in Section 5 and Section 6, respectively.
2 Preliminaries
2.1 Basic notations
We work in the ![]() $(3+1)$ dimensional spacetime with metric
$(3+1)$ dimensional spacetime with metric ![]() $\eta = \text {diag} (-1, 1, 1, 1)$. We write a point
$\eta = \text {diag} (-1, 1, 1, 1)$. We write a point ![]() $(x^0, x^a) = (t, x^a)$, and the indices are raised or lowered by the metric
$(x^0, x^a) = (t, x^a)$, and the indices are raised or lowered by the metric ![]() $\eta $. We use
$\eta $. We use
 $$ \begin{align*} \begin{aligned} &{\partial}_\alpha = {\partial}_{x^\alpha}, &\qquad \qquad \alpha = 0, 1, 2, 3,\\ &\Omega_{ab} = x_a {\partial}_b - x_b {\partial}_a, &\qquad \qquad a, b = 1, 2, 3, \text{ and } a<b, \\ &L_a = x_a {\partial}_t + t {\partial}_a, &\qquad \qquad a = 1, 2, 3 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\partial}_\alpha = {\partial}_{x^\alpha}, &\qquad \qquad \alpha = 0, 1, 2, 3,\\ &\Omega_{ab} = x_a {\partial}_b - x_b {\partial}_a, &\qquad \qquad a, b = 1, 2, 3, \text{ and } a<b, \\ &L_a = x_a {\partial}_t + t {\partial}_a, &\qquad \qquad a = 1, 2, 3 \end{aligned} \end{align*} $$to denote the vector fields of translation, rotation and Lorentz boosts, respectively. For convenience, we use ![]() ${\partial }, \Omega , L$ to represent a general vector field of translation, rotation and Lorentz boost, respectively; and with the notation
${\partial }, \Omega , L$ to represent a general vector field of translation, rotation and Lorentz boost, respectively; and with the notation
![]() $\Gamma $ is used to represent a general vector field in V.
$\Gamma $ is used to represent a general vector field in V.
When it turns to the hyperboloidal foliation of the spacetime of the cone ![]() $\mathcal {K} := \{(t, x) : t \geq t_0 = 2, t \geq |x| + 1 \}$, we use
$\mathcal {K} := \{(t, x) : t \geq t_0 = 2, t \geq |x| + 1 \}$, we use ![]() $\mathcal {H}_s = \{(t, x) : t^2 = |x|^2 + s^2 \}$ to denote a hyperboloid at hyperbolic time s with
$\mathcal {H}_s = \{(t, x) : t^2 = |x|^2 + s^2 \}$ to denote a hyperboloid at hyperbolic time s with ![]() $s \geq s_0 = 2$. We note that throughout we will only consider (unless specified) functions with support in
$s \geq s_0 = 2$. We note that throughout we will only consider (unless specified) functions with support in ![]() $\mathcal {K}$, since the solution to equation (1.1) is supported in
$\mathcal {K}$, since the solution to equation (1.1) is supported in ![]() $\mathcal {K}$. We emphasize here that for all points
$\mathcal {K}$. We emphasize here that for all points ![]() $(t, x) \in \mathcal {K} \bigcap \mathcal {H}_s$ (
$(t, x) \in \mathcal {K} \bigcap \mathcal {H}_s$ (![]() $s \geq 2$), the following relations hold:
$s \geq 2$), the following relations hold:
In order to adapt to the hyperboloidal foliation of the spacetime, we first recall the semi-hyperboloidal frame introduced in [Reference LeFloch and Ma16], which is defined by
We can also represent the usual partial derivatives ![]() ${\partial }_\alpha $ in terms of the semi-hyperboloidal frame by
${\partial }_\alpha $ in terms of the semi-hyperboloidal frame by
We denote the Fourier transform of a nice function u by
We recall some properties regarding the Fourier transform, which will be used in the analysis. The partial derivatives are reflected by Fourier multipliers
and the Plancheral identity connects the ![]() $L^2$ norms between the function and its Fourier transform
$L^2$ norms between the function and its Fourier transform
2.2 Estimates for commutators and null forms
Estimates for commutators
We first demonstrate some well-known results regarding the commutators of different vector fields, which can be found in [Reference Sogge26, Reference LeFloch and Ma16].
Lemma 2.1. Let u be a sufficiently regular function with support ![]() $\mathcal {K}$, and denote the commutator by
$\mathcal {K}$, and denote the commutator by ![]() $[\Gamma , \Gamma '] = \Gamma \Gamma '- \Gamma '\Gamma $; then we have
$[\Gamma , \Gamma '] = \Gamma \Gamma '- \Gamma '\Gamma $; then we have
 $$ \begin{align} \begin{aligned} \big|[{\partial}_\alpha, L_a] u \big| + \big| [{\partial}_\alpha, \Omega_{ab}] u \big| &\lesssim \sum_\beta \big| {\partial}_\beta u \big|,\\ \big| [L_c, \Omega_{ab}] u \big| + \big| [L_a, L_b] u \big| &\lesssim \sum_{d} \big| L_d u \big|,\\ \big| [L_a, (s/t)] u \big| &\lesssim \big| (s/t) u \big|,\\ \big| [L_b L_a, (s/t)] u \big| &\lesssim \big| (s/t) u \big| + \sum_c \big| (s/t) L_c u \big|,\\ \big| [\underline{\partial}_a, L_b] u \big| &\lesssim \sum_c \big| \underline{\partial}_c u \big|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big|[{\partial}_\alpha, L_a] u \big| + \big| [{\partial}_\alpha, \Omega_{ab}] u \big| &\lesssim \sum_\beta \big| {\partial}_\beta u \big|,\\ \big| [L_c, \Omega_{ab}] u \big| + \big| [L_a, L_b] u \big| &\lesssim \sum_{d} \big| L_d u \big|,\\ \big| [L_a, (s/t)] u \big| &\lesssim \big| (s/t) u \big|,\\ \big| [L_b L_a, (s/t)] u \big| &\lesssim \big| (s/t) u \big| + \sum_c \big| (s/t) L_c u \big|,\\ \big| [\underline{\partial}_a, L_b] u \big| &\lesssim \sum_c \big| \underline{\partial}_c u \big|. \end{aligned} \end{align} $$Next, we recall the following result from [Reference Sogge26], which tells us that the null forms acted by a vector field still give us null forms.
Lemma 2.2. For all nice functions ![]() $u, w$, we have
$u, w$, we have
 $$ \begin{align} \begin{aligned} {\partial}_\alpha Q_0 (u, w) - Q_0 ({\partial}_\alpha u, w) - Q_0 (u, {\partial}_\alpha w) & = 0,\\ {\partial}_\gamma Q_{\alpha \beta} (u, w) - Q_{\alpha \beta} ({\partial}_\gamma u, w) - Q_{\alpha \beta} (u, {\partial}_\gamma w) &= 0,\\ L_a Q_0 (u, w) - Q_0 (L_a u, w) - Q_0 (u, L_a w) &= 0,\\ \big| L_a Q_{\alpha \beta} (u, w) - Q_{\alpha \beta} (L_a u, w) - Q_{\alpha \beta} (u, L_a w) \big| &\leq \sum_{\alpha', \beta'} \big| Q_{\alpha' \beta'} (u, w) \big|. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\partial}_\alpha Q_0 (u, w) - Q_0 ({\partial}_\alpha u, w) - Q_0 (u, {\partial}_\alpha w) & = 0,\\ {\partial}_\gamma Q_{\alpha \beta} (u, w) - Q_{\alpha \beta} ({\partial}_\gamma u, w) - Q_{\alpha \beta} (u, {\partial}_\gamma w) &= 0,\\ L_a Q_0 (u, w) - Q_0 (L_a u, w) - Q_0 (u, L_a w) &= 0,\\ \big| L_a Q_{\alpha \beta} (u, w) - Q_{\alpha \beta} (L_a u, w) - Q_{\alpha \beta} (u, L_a w) \big| &\leq \sum_{\alpha', \beta'} \big| Q_{\alpha' \beta'} (u, w) \big|. \end{aligned} \end{align} $$Estimates for null forms
We first recall the classical estimates for null forms of the type ![]() $Q_{\alpha \beta }$, which can be found in [Reference Sogge26].
$Q_{\alpha \beta }$, which can be found in [Reference Sogge26].
Lemma 2.3. We have for sufficiently regular functions ![]() $u, w$ with support in
$u, w$ with support in ![]() $\mathcal {K} = \{ (t, x) : t \geq t_0, t \geq |x| + 1 \}$
$\mathcal {K} = \{ (t, x) : t \geq t_0, t \geq |x| + 1 \}$
In addition, following from [Reference LeFloch and Ma17] of the hyperboloidal setting, we also have the following estimates for all types of null forms.
Lemma 2.4. It holds for smooth functions ![]() $u, w$ with support in
$u, w$ with support in ![]() $\mathcal {K} = \{ (t, x) : t \geq t_0, t \geq |x| + 1 \}$ that
$\mathcal {K} = \{ (t, x) : t \geq t_0, t \geq |x| + 1 \}$ that
Proof. We revisit the proof for ![]() $Q_0 (u, w)$ only, from [Reference LeFloch and Ma16], for readers who are not familiar with the hyperboloidal foliation method.
$Q_0 (u, w)$ only, from [Reference LeFloch and Ma16], for readers who are not familiar with the hyperboloidal foliation method.
Recall the semi-hyperboloidal frame
and we express the null form ![]() $Q_0 (u, w)$ in the semi-hyperboloidal frame to get
$Q_0 (u, w)$ in the semi-hyperboloidal frame to get
Then the fact ![]() $|x| \leq t$ concludes the estimates.
$|x| \leq t$ concludes the estimates.
2.3 Sobolev–type inequalities
Klainerman-Sobolev inequality
In order to obtain pointwise decay estimates for the Klein-Gordon components, we need the following Klainerman-Sobolev inequality, which was introduced in [Reference Klainerman13]. We need the following version of Klainerman-Sobolev inequality because it will not need to rely on the scaling vector field ![]() $L_0 = t {\partial }_t + x^a {\partial }_a$ (which is not consistent with the Klein-Gordon equations), and this feature is vital in obtaining the mass-independent pointwise decay results for the Klein-Gordon components.
$L_0 = t {\partial }_t + x^a {\partial }_a$ (which is not consistent with the Klein-Gordon equations), and this feature is vital in obtaining the mass-independent pointwise decay results for the Klein-Gordon components.
Proposition 2.5. Assume ![]() $u = u(t, x)$ is a sufficiently smooth function that decays sufficiently fast at space infinity for each fixed
$u = u(t, x)$ is a sufficiently smooth function that decays sufficiently fast at space infinity for each fixed ![]() $t \geq 2$; then for any
$t \geq 2$; then for any ![]() $t \geq 2$,
$t \geq 2$, ![]() $x \in \mathbb {R}^3$, we have
$x \in \mathbb {R}^3$, we have
We will use a simplified version of Proposition 2.5 where we do not need to use the rotation vector field because we only need to consider functions supported in ![]() $\mathcal {K} = \{(t, x) : t \geq 2, t \geq |x| + 1 \}$.
$\mathcal {K} = \{(t, x) : t \geq 2, t \geq |x| + 1 \}$.
Proposition 2.6. Assume ![]() $u = u(t, x)$ is a sufficiently smooth function with support
$u = u(t, x)$ is a sufficiently smooth function with support ![]() $\mathcal {K}$; then for any
$\mathcal {K}$; then for any ![]() $t \geq 2$,
$t \geq 2$, ![]() $x \in \mathbb {R}^3$, we have
$x \in \mathbb {R}^3$, we have
Sobolev-type inequality on hyperboloids
We now recall a Sobolev-type inequality adapted to the hyperboloids from [Reference LeFloch and Ma16], which allows us to get the (mass-dependent) sup-norm estimates for the Klein-Gordon components.
Proposition 2.7. Let ![]() $u= u(t, x)$ be a sufficiently nice function with support
$u= u(t, x)$ be a sufficiently nice function with support ![]() $\{(t, x): t \geq |x| + 1\}$; then for all
$\{(t, x): t \geq |x| + 1\}$; then for all ![]() $s \geq 2$, one has
$s \geq 2$, one has
where the symbol L denotes the Lorentz boosts.
The Sobolev inequality in equation (2.12) combined with the commutator estimates gives us the following inequality:
Hardy inequality on hyperboloids
Proposition 2.8. Let ![]() $u = u(x)$ be a sufficiently smooth function in dimension
$u = u(x)$ be a sufficiently smooth function in dimension ![]() $d \geq 3$; then it holds (
$d \geq 3$; then it holds (![]() $r = |x|$)
$r = |x|$)
The Hardy inequality can also be adapted to the hyperboloidal setting; see, for instance, [Reference LeFloch and Ma16, Reference LeFloch and Ma17].
Proposition 2.9. Assume the function u is sufficiently regular and supported in the region ![]() $\mathcal {K}$; then for all
$\mathcal {K}$; then for all ![]() $s\geq 2$, one has
$s\geq 2$, one has
As a consequence, we also have
Sobolev embedding theorem
We recall the following type of Sobolev embedding theorem.
Proposition 2.10. Let ![]() $u = u(x) \in L^{6/5}(\mathbb {R}^3)$; then it holds that
$u = u(x) \in L^{6/5}(\mathbb {R}^3)$; then it holds that
in which ![]() $\Lambda = \sqrt {- \Delta } = \sqrt {- {\partial }_a {\partial }^a}$.
$\Lambda = \sqrt {- \Delta } = \sqrt {- {\partial }_a {\partial }^a}$.
2.4 Energy estimates for Klein-Gordon equations
Given a function ![]() $u = u(t, x)$ supported in
$u = u(t, x)$ supported in ![]() $\mathcal {K}$, we define its energy
$\mathcal {K}$, we define its energy ![]() $\mathcal {E}_m$, following [Reference LeFloch and Ma16], on a hyperboloid
$\mathcal {E}_m$, following [Reference LeFloch and Ma16], on a hyperboloid ![]() $\mathcal {H}_s$ by
$\mathcal {H}_s$ by
 $$ \begin{align} \begin{aligned} \mathcal{E}_m(s, u) &:= \int_{\mathcal{H}_s} \Big( \big({\partial}_t u \big)^2+ \sum_a \big({\partial}_a u \big)^2+ 2 (x^a/t) {\partial}_t u {\partial}_a u + m^2 u^2 \Big) \, dx\\ &= \int_{\mathcal{H}_s} \Big( \big( (s/t){\partial}_t u \big)^2+ \sum_a \big(\underline{\partial}_a u \big)^2+ m^2 u^2 \Big) \, dx\\ &= \int_{\mathcal{H}_s} \Big( \big( \underline{\partial}_\perp u \big)^2+ \sum_a \big( (s/t){\partial}_a u \big)^2+ \sum_{a<b} \big( t^{-1}\Omega_{ab} u \big)^2+ m^2 u^2 \Big) \, dx, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal{E}_m(s, u) &:= \int_{\mathcal{H}_s} \Big( \big({\partial}_t u \big)^2+ \sum_a \big({\partial}_a u \big)^2+ 2 (x^a/t) {\partial}_t u {\partial}_a u + m^2 u^2 \Big) \, dx\\ &= \int_{\mathcal{H}_s} \Big( \big( (s/t){\partial}_t u \big)^2+ \sum_a \big(\underline{\partial}_a u \big)^2+ m^2 u^2 \Big) \, dx\\ &= \int_{\mathcal{H}_s} \Big( \big( \underline{\partial}_\perp u \big)^2+ \sum_a \big( (s/t){\partial}_a u \big)^2+ \sum_{a<b} \big( t^{-1}\Omega_{ab} u \big)^2+ m^2 u^2 \Big) \, dx, \end{aligned} \end{align} $$in which ![]() $\underline {\partial }_{\perp } := {\partial }_t+ (x^a / t) {\partial }_a$ is the orthogonal vector field. The integral
$\underline {\partial }_{\perp } := {\partial }_t+ (x^a / t) {\partial }_a$ is the orthogonal vector field. The integral ![]() $L^2_f(\mathcal {H}_s)$ is defined by
$L^2_f(\mathcal {H}_s)$ is defined by
 $$ \begin{align} \| u \|_{L^2_f(\mathcal{H}_s)}^2 :=\int_{\mathcal{H}_s}| u |^2 \, dx :=\int_{\mathbb{R}^3} \big| u(\sqrt{s^2+|x|^2}, x) \big|^2 \, dx. \end{align} $$
$$ \begin{align} \| u \|_{L^2_f(\mathcal{H}_s)}^2 :=\int_{\mathcal{H}_s}| u |^2 \, dx :=\int_{\mathbb{R}^3} \big| u(\sqrt{s^2+|x|^2}, x) \big|^2 \, dx. \end{align} $$We note that it holds
which will be used frequently.
Next, we demonstrate the energy estimates in the hyperboloidal setting.
Proposition 2.11 Energy estimates for wave-Klein-Gordon equations
For ![]() $m \geq 0$ and for
$m \geq 0$ and for ![]() $s \geq s_0$ (with
$s \geq s_0$ (with ![]() $s_0 = 2$), it holds that
$s_0 = 2$), it holds that
for all sufficiently regular functions u, which are defined and supported in ![]() $\mathcal {K}_{[s_0, s]} = \bigcup _{s_0 \leq s'\leq s} \mathcal {H}_{s'}$.
$\mathcal {K}_{[s_0, s]} = \bigcup _{s_0 \leq s'\leq s} \mathcal {H}_{s'}$.
The proof of equation (2.20) can be found in [Reference LeFloch and Ma16, Reference LeFloch and Ma17].
In comparison with ![]() $\mathcal {E}_m$, we use
$\mathcal {E}_m$, we use ![]() $E_m$ to denote the usual energy on the flat slices
$E_m$ to denote the usual energy on the flat slices ![]() $t = constant$, which is expressed as
$t = constant$, which is expressed as
Similarly, we have the following energy estimate:
 $$ \begin{align} E_m(t, u)^{1/2} \leq E_m(t_0, u)^{1/2} + \int_2^t \big\| -\Box u + m^2 u \big\|_{L^2(\mathbb{R}^3)} \, dt'. \end{align} $$
$$ \begin{align} E_m(t, u)^{1/2} \leq E_m(t_0, u)^{1/2} + \int_2^t \big\| -\Box u + m^2 u \big\|_{L^2(\mathbb{R}^3)} \, dt'. \end{align} $$3 Mass-independent  $L^2$ norm estimates for Klein-Gordon equations
$L^2$ norm estimates for Klein-Gordon equations
We will rely on the following key proposition to obtain the mass-independent ![]() $L^2$–type energy estimates for the solution to the system in equation (1.1). A similar result was previously obtained in [Reference Dong3], and we now provide an enhanced version of it. We note that the improvements compared with the results in [Reference Dong3] mainly include the following: 1) the norm for the right-hand side source is taken to be
$L^2$–type energy estimates for the solution to the system in equation (1.1). A similar result was previously obtained in [Reference Dong3], and we now provide an enhanced version of it. We note that the improvements compared with the results in [Reference Dong3] mainly include the following: 1) the norm for the right-hand side source is taken to be ![]() $\| \cdot \|_{L^{6/5}(\mathbb {R}^3)}$ in Proposition 3.1 instead of the previous weighted
$\| \cdot \|_{L^{6/5}(\mathbb {R}^3)}$ in Proposition 3.1 instead of the previous weighted ![]() $\| |x| \cdot \|_{L^2(\mathbb {R}^3)}$ of [Reference Dong3], which allows us to benefit from more decay rates in many cases; 2) the norm for the right-hand side source is without r-weight in Proposition 3.1 compared with the result in [Reference Dong3], and this is expected to treat the non-compactly supported case where it is much better to get rid of the r-weight in the region
$\| |x| \cdot \|_{L^2(\mathbb {R}^3)}$ of [Reference Dong3], which allows us to benefit from more decay rates in many cases; 2) the norm for the right-hand side source is without r-weight in Proposition 3.1 compared with the result in [Reference Dong3], and this is expected to treat the non-compactly supported case where it is much better to get rid of the r-weight in the region ![]() $r \gg t$.
$r \gg t$.
Proposition 3.1. Consider the wave-Klein-Gordon equation
with mass ![]() $m \in [0, 1]$, and assume
$m \in [0, 1]$, and assume
for some numbers ![]() $C_{t_0}$ and
$C_{t_0}$ and ![]() $C_f$. Then we have
$C_f$. Then we have
 $$ \begin{align} \| u \|_{L^2(\mathbb{R}^3)} \lesssim \left\{ \begin{array}{lll} C_{t_0} + C_f t^q, & \quad q>0, \\ C_{t_0} + C_f \log t, & \quad q = 0, \\ C_{t_0} + C_f, & \quad q<0. \end{array} \right. \end{align} $$
$$ \begin{align} \| u \|_{L^2(\mathbb{R}^3)} \lesssim \left\{ \begin{array}{lll} C_{t_0} + C_f t^q, & \quad q>0, \\ C_{t_0} + C_f \log t, & \quad q = 0, \\ C_{t_0} + C_f, & \quad q<0. \end{array} \right. \end{align} $$Proof. We first write the equation of u in the Fourier space ![]() $(t, \xi )$
$(t, \xi )$
and solve the ordinary differential equation to get the solution
 $$ \begin{align*}\widehat{u}(t, \xi) = \cos\big( t \xi_m \big) \widehat{u}_0 + { \sin\big( t \xi_m \big) \over \xi_m } \widehat{u}_1 + {1\over \xi_m} \int_{t_0}^{t} \sin\big( (t-t') \xi_m \big) \widehat{f}(t') \, dt', \end{align*} $$
$$ \begin{align*}\widehat{u}(t, \xi) = \cos\big( t \xi_m \big) \widehat{u}_0 + { \sin\big( t \xi_m \big) \over \xi_m } \widehat{u}_1 + {1\over \xi_m} \int_{t_0}^{t} \sin\big( (t-t') \xi_m \big) \widehat{f}(t') \, dt', \end{align*} $$with the notations defined by
Next, we take the ![]() $L^2$ norm in the frequency space to obtain
$L^2$ norm in the frequency space to obtain
 $$ \begin{align*} \begin{aligned} &\big\| \widehat{u}(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \big\| \cos\big( t \xi_m \big) \widehat{u}_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { \sin\big( t \xi_m \big) \over \xi_m } \widehat{u}_1 \Big\|_{L^2(\mathbb{R}^3)} + \Big\| {1\over \xi_m} \int_{t_0}^{t} \sin\big( (t-t') \xi_m \big) \widehat{f}(t') \, dt' \Big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \big\| \widehat{u}_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { 1 \over |\xi| } \widehat{u}_1 \Big\|_{L^2(\mathbb{R}^3)} + \int_{t_0}^{t} \Big\| {1\over |\xi|} \widehat{f}(t') \Big\|_{L^2(\mathbb{R}^3)} \, dt', \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\big\| \widehat{u}(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \big\| \cos\big( t \xi_m \big) \widehat{u}_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { \sin\big( t \xi_m \big) \over \xi_m } \widehat{u}_1 \Big\|_{L^2(\mathbb{R}^3)} + \Big\| {1\over \xi_m} \int_{t_0}^{t} \sin\big( (t-t') \xi_m \big) \widehat{f}(t') \, dt' \Big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \big\| \widehat{u}_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { 1 \over |\xi| } \widehat{u}_1 \Big\|_{L^2(\mathbb{R}^3)} + \int_{t_0}^{t} \Big\| {1\over |\xi|} \widehat{f}(t') \Big\|_{L^2(\mathbb{R}^3)} \, dt', \end{aligned} \end{align*} $$which in the physical space reads
 $$ \begin{align*} \big\| u(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \lesssim \big\| u_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { u_1 \over \Lambda } \Big\|_{L^2(\mathbb{R}^3)} + \int_{t_0}^{t} \Big\| {f (t')\over \Lambda} \Big\|_{L^2(\mathbb{R}^3)} \, dt', \end{align*} $$
$$ \begin{align*} \big\| u(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \lesssim \big\| u_0 \big\|_{L^2(\mathbb{R}^3)} +\Big\| { u_1 \over \Lambda } \Big\|_{L^2(\mathbb{R}^3)} + \int_{t_0}^{t} \Big\| {f (t')\over \Lambda} \Big\|_{L^2(\mathbb{R}^3)} \, dt', \end{align*} $$with ![]() $\Lambda = \sqrt {-{\partial }_a {\partial }^a}$.
$\Lambda = \sqrt {-{\partial }_a {\partial }^a}$.
Then by the Sobolev embedding theorem in equation (2.17), we admit
 $$ \begin{align*}\big\| u(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \lesssim \big\| u_0 \big\|_{L^2(\mathbb{R}^3)} +\big\| u_1 \big\|_{L^{6/5}(\mathbb{R}^3)} + \int_{t_0}^{t} \big\| f (t') \big\|_{L^{6/5}(\mathbb{R}^3)} \, dt', \end{align*} $$
$$ \begin{align*}\big\| u(t, \cdot) \big\|_{L^2(\mathbb{R}^3)} \lesssim \big\| u_0 \big\|_{L^2(\mathbb{R}^3)} +\big\| u_1 \big\|_{L^{6/5}(\mathbb{R}^3)} + \int_{t_0}^{t} \big\| f (t') \big\|_{L^{6/5}(\mathbb{R}^3)} \, dt', \end{align*} $$and the simple result of the integral
 $$ \begin{align*}\int_{t_0}^t t^{\prime -1 + q} \, dt' \end{align*} $$
$$ \begin{align*}\int_{t_0}^t t^{\prime -1 + q} \, dt' \end{align*} $$implies the desired result of equation (3.1).
We note in the proof that to obtain the ![]() $L^2$–type energy estimates for the solution, we transformed the original equation to the Fourier space, solved the corresponding ordinary differential equation and then conducted the analysis. It is worth mentioning that we find such procedures to bound the
$L^2$–type energy estimates for the solution, we transformed the original equation to the Fourier space, solved the corresponding ordinary differential equation and then conducted the analysis. It is worth mentioning that we find such procedures to bound the ![]() $L^2$–type norms for Klein-Gordon equations (with possibly vanishing mass) can also be applied to pure wave equations, especially in the low dimension where the conformal energy cannot bound the
$L^2$–type norms for Klein-Gordon equations (with possibly vanishing mass) can also be applied to pure wave equations, especially in the low dimension where the conformal energy cannot bound the ![]() $L^2$ norm of the solution; see, for instance, [Reference Dong4].
$L^2$ norm of the solution; see, for instance, [Reference Dong4].
As a consequence, combined with the Klainerman-Sobolev inequality in equation (2.10), we also get
 $$ \begin{align} \| u \|_{L^\infty(\mathbb{R}^3)} \lesssim \left\{ \begin{array}{lll} C_{t_0} t^{-1} + C_f t^{-1+q}, & \quad q>0,\\ C_{t_0} t^{-1} + C_f t^{-1} \log t, & \quad q = 0,\\ C_{t_0} t^{-1} + C_f t^{-1}, & \quad q<0, \end{array} \right. \end{align} $$
$$ \begin{align} \| u \|_{L^\infty(\mathbb{R}^3)} \lesssim \left\{ \begin{array}{lll} C_{t_0} t^{-1} + C_f t^{-1+q}, & \quad q>0,\\ C_{t_0} t^{-1} + C_f t^{-1} \log t, & \quad q = 0,\\ C_{t_0} t^{-1} + C_f t^{-1}, & \quad q<0, \end{array} \right. \end{align} $$if additional information for higher-order energy is true (with ![]() $\Gamma \in \{{\partial }, \Omega , L \}$)
$\Gamma \in \{{\partial }, \Omega , L \}$)
4 Proof for the global existence result
4.1 Initialisation of the bootstrap method
In this section, we aim to prove the uniform global existence result for the system in equation (1.1) via the hyperboloidal foliation method.
As usual, we will rely on the bootstrap method. The local well-posedness result allows us to assume (for all i)
for all ![]() $s \in [s_0, s_1)$ with
$s \in [s_0, s_1)$ with ![]() $s_1> s_0$. In equation (4.1),
$s_1> s_0$. In equation (4.1), ![]() $C_1 \gg 1$ is some large constant to be determined, and
$C_1 \gg 1$ is some large constant to be determined, and ![]() ${\epsilon }> 0$ is the size of the initial data satisfying
${\epsilon }> 0$ is the size of the initial data satisfying ![]() $C_1 {\epsilon } \ll \delta \ll 1$, and
$C_1 {\epsilon } \ll \delta \ll 1$, and ![]() $s_1$ is defined by
$s_1$ is defined by
If ![]() $s_1 = + \infty $, then the global existence result is done. So in the following proof, we first assume
$s_1 = + \infty $, then the global existence result is done. So in the following proof, we first assume ![]() $s_1 < + \infty $ and then deduce contradictions to assert that
$s_1 < + \infty $ and then deduce contradictions to assert that ![]() $s_1$ must be
$s_1$ must be ![]() $+\infty $.
$+\infty $.
By recalling the definition of the energy ![]() $\mathcal {E}_m$, we easily have the following estimates.
$\mathcal {E}_m$, we easily have the following estimates.
Lemma 4.1. Assume equation (4.1) holds; then for all ![]() $s \in [s_0, s_1)$ and
$s \in [s_0, s_1)$ and ![]() $|I| + |J| \leq N$, we have the following estimates:
$|I| + |J| \leq N$, we have the following estimates:
 $$ \begin{align} \begin{aligned} \big\| (s/t) {\partial} {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} + m \big\| {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} + \sum_a \big\| \underline{\partial}_a {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} &\lesssim C_1 \epsilon,\\ \big\| (s/t) {\partial}^I L^J {\partial} v_i \big\|_{L^2_f(\mathcal{H}_s)} + \sum_a \big\| {\partial}^I L^J \underline{\partial}_a v_i \big\|_{L^2_f(\mathcal{H}_s)} &\lesssim C_1 \epsilon. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| (s/t) {\partial} {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} + m \big\| {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} + \sum_a \big\| \underline{\partial}_a {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} &\lesssim C_1 \epsilon,\\ \big\| (s/t) {\partial}^I L^J {\partial} v_i \big\|_{L^2_f(\mathcal{H}_s)} + \sum_a \big\| {\partial}^I L^J \underline{\partial}_a v_i \big\|_{L^2_f(\mathcal{H}_s)} &\lesssim C_1 \epsilon. \end{aligned} \end{align} $$Combined with the Sobolev–type inequality on hyperboloids in equation (2.12), the following pointwise estimates are valid.
Lemma 4.2. For all ![]() $|I| + |J| \leq N-2$, we have
$|I| + |J| \leq N-2$, we have
In addition to the estimates above, we also introduce estimates obtained by using the Hardy inequality in equations (2.15)–(2.16). They will not be used in the current section but will be used in Section 5.
Lemma 4.3. The following estimates are valid:
 $$ \begin{align} \begin{aligned} \big\| t^{-1} {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} \lesssim C_1 {\epsilon},\qquad |I| + |J| \leq N,\\ \big| {\partial}^I L^J v_i \big|\lesssim C_1 {\epsilon} t^{-1/2},\qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| t^{-1} {\partial}^I L^J v_i \big\|_{L^2_f(\mathcal{H}_s)} \lesssim C_1 {\epsilon},\qquad |I| + |J| \leq N,\\ \big| {\partial}^I L^J v_i \big|\lesssim C_1 {\epsilon} t^{-1/2},\qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$4.2 Improved energy estimates and global existence result
We now want to show the improved energy estimates for the solution ![]() $v = (v_i)$ and conclude the global existence result.
$v = (v_i)$ and conclude the global existence result.
Proposition 4.4 Improved energy estimates
Let the assumptions in equation (4.1) be true; then for all ![]() $s \in [s_0, s_1)$, it holds that
$s \in [s_0, s_1)$, it holds that
Proof. When the vector field ![]() ${\partial }^I L^J$ with
${\partial }^I L^J$ with ![]() $|I| + |J| \leq N$ acts on the model equations in (1.1), we get
$|I| + |J| \leq N$ acts on the model equations in (1.1), we get
According to the commutator estimates in Lemma 2.2, we can bound the right-hand side as follows:
 $$ \begin{align*} \begin{aligned} &\big| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big|\\ &\quad\lesssim \sum_{\substack{j, k, \alpha, \beta \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \Big( \big| Q_0 ({\partial}^{I_1}L^{J_1} v_j, {\partial}^{I_2}L^{J_2} v_k) \big| + \big| Q_{\alpha \beta} ({\partial}^{I_1}L^{J_1} v_j, {\partial}^{I_2}L^{J_2} v_k) \big| \Big). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\big| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big|\\ &\quad\lesssim \sum_{\substack{j, k, \alpha, \beta \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \Big( \big| Q_0 ({\partial}^{I_1}L^{J_1} v_j, {\partial}^{I_2}L^{J_2} v_k) \big| + \big| Q_{\alpha \beta} ({\partial}^{I_1}L^{J_1} v_j, {\partial}^{I_2}L^{J_2} v_k) \big| \Big). \end{aligned} \end{align*} $$Then the estimates for null forms in the hyperboloidal setting in Lemma 2.4 yield
 $$ \begin{align*} \begin{aligned} &\big| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big|\\ &\quad\lesssim \sum_{\substack{j, k, \alpha, a \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \Big( (s/t)^2 \big| {\partial}_t {\partial}^{I_1}L^{J_1} v_j {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big| \\ & \hskip3.4cm + \big|\underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big| + \big|\underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big|\Big). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\big| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big|\\ &\quad\lesssim \sum_{\substack{j, k, \alpha, a \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \Big( (s/t)^2 \big| {\partial}_t {\partial}^{I_1}L^{J_1} v_j {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big| \\ & \hskip3.4cm + \big|\underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big| + \big|\underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big|\Big). \end{aligned} \end{align*} $$We rely on the energy estimates for Klein-Gordon equations on hyperboloids in equation (2.20) to get
 $$ \begin{align*} \begin{aligned} &\mathcal{E}_m (s, {\partial}^I L^J v_i)^{1/2}\\ &\quad\leq \mathcal{E}_m (s_0, {\partial}^I L^J v_i)^{1/2} + \int_{s_0}^s \big\| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big\|_{L^2_f(\mathcal{H}_{s'})} \, ds'\\ &\quad\lesssim \epsilon + \sum_{\substack{j, k, \alpha, a \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \int_{s_0}^s \Big\| (s/t)^2 \big| {\partial}_t {\partial}^{I_1}L^{J_1} v_j {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big| \\ & \hskip3.4cm + \big|\underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big| + \big|\underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big|\Big\|_{L^2_f(\mathcal{H}_{s'})} \, ds'. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\mathcal{E}_m (s, {\partial}^I L^J v_i)^{1/2}\\ &\quad\leq \mathcal{E}_m (s_0, {\partial}^I L^J v_i)^{1/2} + \int_{s_0}^s \big\| N^{jk}_i {\partial}^I L^J Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i {\partial}^I L^J Q_{\alpha \beta} (v_j, v_k) \big\|_{L^2_f(\mathcal{H}_{s'})} \, ds'\\ &\quad\lesssim \epsilon + \sum_{\substack{j, k, \alpha, a \\ |I_1| + |I_2| \leq |I|, |J_1| + |J_2| \leq |J| }} \int_{s_0}^s \Big\| (s/t)^2 \big| {\partial}_t {\partial}^{I_1}L^{J_1} v_j {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big| \\ & \hskip3.4cm + \big|\underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big| + \big|\underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big|\Big\|_{L^2_f(\mathcal{H}_{s'})} \, ds'. \end{aligned} \end{align*} $$We thus have (sinceFootnote 2 ![]() $N \geq 6$)
$N \geq 6$)
 $$ \begin{align*} \begin{aligned} &\mathcal{E}_m (s, {\partial}^I L^J v_i)^{1/2} \\ &\quad\lesssim \epsilon + \sum_{\substack{j, k, \alpha, a \\ |I_1| + |J_1| \leq N, |I_2| + |J_2| \leq N-2}} \int_{s_0}^s \Big( \big\| (s'/t) {\partial}_t {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| (s'/t) {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \\ &\hskip3.5cm + \big\| (s'/t) \underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| (t/s') \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \\ &\hskip3.5cm + \big\| \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| \underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \Big) \, ds' \\ &\quad\lesssim {\epsilon} + (C_1 {\epsilon})^2 \int_{s_0}^s \big\| t^{-3/2} + t^{-1/2} s^{\prime -1} \big\|_{L^\infty(\mathcal{H}_{s'})} \, ds' \lesssim {\epsilon} + (C_1 {\epsilon})^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\mathcal{E}_m (s, {\partial}^I L^J v_i)^{1/2} \\ &\quad\lesssim \epsilon + \sum_{\substack{j, k, \alpha, a \\ |I_1| + |J_1| \leq N, |I_2| + |J_2| \leq N-2}} \int_{s_0}^s \Big( \big\| (s'/t) {\partial}_t {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| (s'/t) {\partial}_t {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \\ &\hskip3.5cm + \big\| (s'/t) \underline{\partial}_\alpha {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| (t/s') \underline{\partial}_a {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \\ &\hskip3.5cm + \big\| \underline{\partial}_a {\partial}^{I_1}L^{J_1} v_j \big\|_{L^2_f(\mathcal{H}_{s'})} \big\| \underline{\partial}_\alpha {\partial}^{I_2}L^{J_2} v_k \big\|_{L^\infty_f(\mathcal{H}_{s'})} \Big) \, ds' \\ &\quad\lesssim {\epsilon} + (C_1 {\epsilon})^2 \int_{s_0}^s \big\| t^{-3/2} + t^{-1/2} s^{\prime -1} \big\|_{L^\infty(\mathcal{H}_{s'})} \, ds' \lesssim {\epsilon} + (C_1 {\epsilon})^2. \end{aligned} \end{align*} $$Hence the proof is done.
As a consequence of the improved energy estimates in Proposition 4.4, we conclude the global existence result of the system in equation (1.1).
Proof of the global existence result.
We choose ![]() $C_1$ large and
$C_1$ large and ![]() ${\epsilon }$ small such that
${\epsilon }$ small such that
in which C is the hidden constant in equation (4.6), which thus leads us to the improved estimates
If ![]() $s_1> s_0$ is some finite number, then the improved estimates above imply that we can extend the solution
$s_1> s_0$ is some finite number, then the improved estimates above imply that we can extend the solution ![]() $v = (v_i)$ to a strictly larger (hyperbolic) time interval, which contradicts the definition of
$v = (v_i)$ to a strictly larger (hyperbolic) time interval, which contradicts the definition of ![]() $s_1$ in equation (4.2). Hence
$s_1$ in equation (4.2). Hence ![]() $s_1$ must be
$s_1$ must be ![]() $+\infty $, which implies the global existence of the solution
$+\infty $, which implies the global existence of the solution ![]() $v = (v_i)$ to the system in equation (1.1).
$v = (v_i)$ to the system in equation (1.1).
5 Proof for the uniform pointwise decay result
5.1 Decomposition and nonlinear transformation
Our task in this section is to show the unified pointwise decay estimate in equation (1.4)
which corresponds to the usual wave decay and Klein-Gordon decay with ![]() $m = 0, 1$, respectively. This is the bulk of the paper.
$m = 0, 1$, respectively. This is the bulk of the paper.
Recall the system in equation (1.1):
 $$ \begin{align*}\begin{aligned} - \Box v_i + m^2 v_i &= N^{jk}_i Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i Q_{\alpha \beta} (v_j, v_k), \\ \big( v_i, {\partial}_t v_i \big)(t_0) &= \big( v_{i0}, v_{i1} \big). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} - \Box v_i + m^2 v_i &= N^{jk}_i Q_0 (v_j, v_k) + M^{jk \alpha \beta}_i Q_{\alpha \beta} (v_j, v_k), \\ \big( v_i, {\partial}_t v_i \big)(t_0) &= \big( v_{i0}, v_{i1} \big). \end{aligned} \end{align*} $$In order to arrive at equation (1.4), it suffices to show
which is because we already obtain
in Section 4. To achieve equation (5.1), we first do a nonlinear transformation from ![]() $v_i$ to
$v_i$ to ![]() $V_i = v_i + N_i^{jk} v_j v_k$ and then decompose
$V_i = v_i + N_i^{jk} v_j v_k$ and then decompose ![]() $V_i$ into pieces
$V_i$ into pieces
For clarity, we note that we use ![]() $V_{c,i}$ to denote the decomposition with cubic nonlinearities, use
$V_{c,i}$ to denote the decomposition with cubic nonlinearities, use ![]() $V_{m, i}$ to denote the decomposition with nonlinearities with m-dependent factors and use
$V_{m, i}$ to denote the decomposition with nonlinearities with m-dependent factors and use ![]() $V_{n, i}$ to denote the decomposition with null nonlinearities of the type
$V_{n, i}$ to denote the decomposition with null nonlinearities of the type ![]() $Q_{\alpha \beta }$. The functions V’s are solutions to the following (linear) Klein-Gordon equations:
$Q_{\alpha \beta }$. The functions V’s are solutions to the following (linear) Klein-Gordon equations:
 $$ \begin{align} \begin{aligned} - \Box V_i + m^2 V_i &= M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k) - m^2 N_i^{jk} v_j v_k \\ &\quad{}+ N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \\ &\quad{}+ N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big), \\ \big(V_i, {\partial}_t V_i \big) (t_0) &= \big( V_{i0}, V_{i1}\big) := \big(v_{i0} + N_i^{jk} v_{j0} v_{k0}, v_{i1} + N_i^{jk} (v_{j0} v_{k1} + v_{j1} v_{k0}) \big), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} - \Box V_i + m^2 V_i &= M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k) - m^2 N_i^{jk} v_j v_k \\ &\quad{}+ N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \\ &\quad{}+ N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big), \\ \big(V_i, {\partial}_t V_i \big) (t_0) &= \big( V_{i0}, V_{i1}\big) := \big(v_{i0} + N_i^{jk} v_{j0} v_{k0}, v_{i1} + N_i^{jk} (v_{j0} v_{k1} + v_{j1} v_{k0}) \big), \end{aligned} \end{align} $$ $$ \begin{align} \begin{aligned} -\Box V_{c, i} + m^2 V_{c, i}&= N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big)\\ &\quad{}+ N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big),\\ \big(V_{c, i}, {\partial}_t V_{c, i} \big) (t_0)&= \big( V_{i0}, V_{i1}\big), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} -\Box V_{c, i} + m^2 V_{c, i}&= N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big)\\ &\quad{}+ N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big),\\ \big(V_{c, i}, {\partial}_t V_{c, i} \big) (t_0)&= \big( V_{i0}, V_{i1}\big), \end{aligned} \end{align} $$ $$ \begin{align} \begin{aligned} -\Box V_{m, i} + m^2 V_{m, i}&= - m^2 N_i^{jk} v_j v_k,\\ \big(V_{m, i}, {\partial}_t V_{m, i} \big) (t_0)&= (0, 0), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} -\Box V_{m, i} + m^2 V_{m, i}&= - m^2 N_i^{jk} v_j v_k,\\ \big(V_{m, i}, {\partial}_t V_{m, i} \big) (t_0)&= (0, 0), \end{aligned} \end{align} $$as well as
 $$ \begin{align} \begin{aligned} - \Box V_{n, i} + m^2 V_{n, i} &= M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k),\\ \big(V_{n, i}, {\partial}_t V_{n, i} \big) (t_0) &= (0, 0). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} - \Box V_{n, i} + m^2 V_{n, i} &= M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k),\\ \big(V_{n, i}, {\partial}_t V_{n, i} \big) (t_0) &= (0, 0). \end{aligned} \end{align} $$ In addition to the decomposition above, we find it helps to utilise the divergence structure of the null forms of the form ![]() $Q_{\alpha \beta }$ if we further decompose the
$Q_{\alpha \beta }$ if we further decompose the ![]() $V_{n, i}$ part as
$V_{n, i}$ part as
We use ![]() $V_{n,i}^5, V_{n,i}^{\gamma }$ to denote the decomposition with 0 nonlinearities and divergent nonlinearities without
$V_{n,i}^5, V_{n,i}^{\gamma }$ to denote the decomposition with 0 nonlinearities and divergent nonlinearities without ![]() ${\partial }_\gamma $, respectively. Similarly,
${\partial }_\gamma $, respectively. Similarly, ![]() $V_{n,i}^5, V_{n,i}^{\gamma }$ are solutions to the following (linear) Klein-Gordon equations:
$V_{n,i}^5, V_{n,i}^{\gamma }$ are solutions to the following (linear) Klein-Gordon equations:
 $$ \begin{align} \begin{aligned} - \Box V_{n,i}^5 + m^2 V_{n,i}^5 &= 0, \\ \big( V_{n,i}^5, {\partial}_t V_{n,i}^5 \big) (t_0) &= (0, 0), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} - \Box V_{n,i}^5 + m^2 V_{n,i}^5 &= 0, \\ \big( V_{n,i}^5, {\partial}_t V_{n,i}^5 \big) (t_0) &= (0, 0), \end{aligned} \end{align} $$ $$ \begin{align} \begin{aligned} - \Box V_{n,i}^{\gamma} + m^2 V_{n,i}^{\gamma} &= M_i^{jk\gamma\beta} v_j {\partial}_\beta v_k - M_i^{jk\alpha\gamma} v_j {\partial}_\alpha v_k, \\ \big( V_{n,i}^{\gamma}, {\partial}_t V_{n,i}^{\gamma} \big) (t_0) &= (0, 0). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} - \Box V_{n,i}^{\gamma} + m^2 V_{n,i}^{\gamma} &= M_i^{jk\gamma\beta} v_j {\partial}_\beta v_k - M_i^{jk\alpha\gamma} v_j {\partial}_\alpha v_k, \\ \big( V_{n,i}^{\gamma}, {\partial}_t V_{n,i}^{\gamma} \big) (t_0) &= (0, 0). \end{aligned} \end{align} $$5.2 The mass-independent  $L^2$ norm estimates
$L^2$ norm estimates
Recall that our goal is to obtain the following mass-independent ![]() $L^2$ estimates for functions Vs, and we will rely on the bootstrap method one more time to achieve it.
$L^2$ estimates for functions Vs, and we will rely on the bootstrap method one more time to achieve it.
Proposition 5.1. For all ![]() $|I| + |J| \leq N-1$ (and for each i), we have
$|I| + |J| \leq N-1$ (and for each i), we have
and for all ![]() $|I| + |J| = N$, we have
$|I| + |J| = N$, we have
in which ![]() $C_3 \geq C_2 \geq C_1$ are some constants to be determined.
$C_3 \geq C_2 \geq C_1$ are some constants to be determined.
We have the following results, which are a consequence of the pointwise decay estimate
obtained in Section 4.
Lemma 5.2. We have for all ![]() $|I| + |J| \leq N-2$ that
$|I| + |J| \leq N-2$ that
Since we are proving energy estimates for linear equations, we know the solutions already exist. We first prove the energy estimates for the low-order cases. By the continuity of the energy, we assume the following bounds are valid for all ![]() $t \in [t_0, t_1)$:
$t \in [t_0, t_1)$:
 $$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_2 {\epsilon}, \qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_2 {\epsilon}, \qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$Similar to the definition of ![]() $s_1$ in Section 4,
$s_1$ in Section 4, ![]() $t_1$ is defined by
$t_1$ is defined by
A direct result from the bootstrap assumption in equation (5.13) is the following.
Lemma 5.3. For all ![]() $t \in [t_0, t_1)$, we have
$t \in [t_0, t_1)$, we have
 $$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^\delta, \qquad |I| + |J| = N-2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^\delta, \qquad |I| + |J| = N-2. \end{aligned} \end{align} $$Proof. For all ![]() $|I| + |J| \leq N-3$, we first have
$|I| + |J| \leq N-3$, we first have
which simply follows from the relations
and the commutator estimate in Lemma 2.1
Next, we recall it holds that
Thus we get
 $$ \begin{align*}\begin{aligned} &\sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J V_i \big\|_{L^2(\mathbb{R}^3)} + \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^\infty(\mathbb{R}^3)}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^2(\mathbb{R}^3)} \\ &\quad\lesssim \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J V_i \big\|_{L^2(\mathbb{R}^3)} + \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J v_i \big\|_{L^\infty(\mathbb{R}^3)}, \end{aligned} \end{align*} $$and the pointwise estimate obtained in Lemma 4.3 yields
and the smallness of ![]() $C_1 {\epsilon }$ allows us finally to obtain
$C_1 {\epsilon }$ allows us finally to obtain
The bound for the case of ![]() $|I| + |J| = N-2$ can be derived in the same way; hence the proof is complete.
$|I| + |J| = N-2$ can be derived in the same way; hence the proof is complete.
We are going to derive the improved estimates under the bootstrap assumption of equation (5.13), and we first provide the improved estimates for low-order cases.
Proposition 5.4. Let the estimate in equation (5.13) be true; then for any ![]() $t \in [t_0, t_1)$, we have
$t \in [t_0, t_1)$, we have
 $$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_2 {\epsilon})^2, \qquad |I| + |J| \leq N-3, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_2 {\epsilon})^2, \qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_2 {\epsilon})^2, \qquad |I| + |J| \leq N-3, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_2 {\epsilon})^2, \qquad |I| + |J| \leq N-2. \end{aligned} \end{align} $$Proof. In terms of the features of each term, we estimate them one by one.
Estimate for ![]() $\big \| {\partial }^I L^J V_{m, i} \big \|_{L^2(\mathbb {R}^3)}$. We start with the easy one, and the energy estimate for the
$\big \| {\partial }^I L^J V_{m, i} \big \|_{L^2(\mathbb {R}^3)}$. We start with the easy one, and the energy estimate for the ![]() ${\partial }^I L^J V_{m, i}$ equation gives
${\partial }^I L^J V_{m, i}$ equation gives
 $$ \begin{align*}E_m (t, {\partial}^I L^J V_{m, i})^{1/2} \leq E_m (t_0, {\partial}^I L^J V_{m, i})^{1/2} + \int_{t_0}^t \big\| {\partial}^I L^J F_{V_{m, i}} \big\|_{L^2(\mathbb{R}^3)} \, dt', \end{align*} $$
$$ \begin{align*}E_m (t, {\partial}^I L^J V_{m, i})^{1/2} \leq E_m (t_0, {\partial}^I L^J V_{m, i})^{1/2} + \int_{t_0}^t \big\| {\partial}^I L^J F_{V_{m, i}} \big\|_{L^2(\mathbb{R}^3)} \, dt', \end{align*} $$with
Recall the m-dependent pointwise estimate
and we get
 $$ \begin{align*}\begin{aligned} E_m (t, {\partial}^I L^J V_{m, i})^{1/2} &\lesssim m^2 {\epsilon} + m \int_{t_0}^t \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| m {\partial}^I L^J v \big\|_{L^\infty (\mathbb{R}^3)} \, dt' \\ &\quad\lesssim m^2 {\epsilon} +m C_1 {\epsilon} C_2 {\epsilon} \int_{t_0}^t t^{\prime -3/2 + \delta} \, dt' \lesssim m C_1 {\epsilon} C_2 {\epsilon}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} E_m (t, {\partial}^I L^J V_{m, i})^{1/2} &\lesssim m^2 {\epsilon} + m \int_{t_0}^t \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| m {\partial}^I L^J v \big\|_{L^\infty (\mathbb{R}^3)} \, dt' \\ &\quad\lesssim m^2 {\epsilon} +m C_1 {\epsilon} C_2 {\epsilon} \int_{t_0}^t t^{\prime -3/2 + \delta} \, dt' \lesssim m C_1 {\epsilon} C_2 {\epsilon}. \end{aligned} \end{align*} $$Hence the definition of the energy ![]() $E_m$ implies that
$E_m$ implies that
Estimates for ![]() $\big \| {\partial }^I L^J V_{c, i} \big \|_{L^2(\mathbb {R}^3)}$,
$\big \| {\partial }^I L^J V_{c, i} \big \|_{L^2(\mathbb {R}^3)}$, ![]() $\big \| {\partial }^I L^J V_{n, i} \big \|_{L^2(\mathbb {R}^3)}$,
$\big \| {\partial }^I L^J V_{n, i} \big \|_{L^2(\mathbb {R}^3)}$, ![]() $\big \| {\partial }^I L^J V_{n, i}^5 \big \|_{L^2(\mathbb {R}^3)}$. Since the procedure is the same when estimating these three solutions, we gather the proof here.
$\big \| {\partial }^I L^J V_{n, i}^5 \big \|_{L^2(\mathbb {R}^3)}$. Since the procedure is the same when estimating these three solutions, we gather the proof here.
For the equations with fast-decay nonlinearities, which is the situation now, we rely on Proposition 3.1 to obtain the m-independent ![]() $L^2$ norm bounds. Thus it suffices to estimate
$L^2$ norm bounds. Thus it suffices to estimate ![]() $\| \text {nonlinearities} \|_{L^{6/5}(\mathbb {R}^3)}$.
$\| \text {nonlinearities} \|_{L^{6/5}(\mathbb {R}^3)}$.
We find for estimating ![]() $\big \| {\partial }^I L^J V_{c, i} \big \|_{L^2(\mathbb {R}^3)}$ it suffices to show that
$\big \| {\partial }^I L^J V_{c, i} \big \|_{L^2(\mathbb {R}^3)}$ it suffices to show that
 $$ \begin{align*}\begin{aligned} & \sum_{|I| + |J| \leq N-2} \Big\| {\partial}^I L^J \Big( N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \\ &\hskip2cm + N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \Big) \Big\|_{L^{6/5}(\mathbb{R}^3)} \\ &\quad\lesssim \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^6(\mathbb{R}^3)}^2 \\ &\quad\lesssim C_2 {\epsilon} t^\delta \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^2}^{2/3} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^\infty}^{4/3} \\ &\quad\lesssim C_2 {\epsilon} (C_1 {\epsilon})^2 t^{-4/3 + 2 \delta}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} & \sum_{|I| + |J| \leq N-2} \Big\| {\partial}^I L^J \Big( N_i^{jk} v_k \big( N_j^{mn} Q_0 (v_m, v_n) + M_j^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \\ &\hskip2cm + N_i^{jk} v_j \big( N_k^{mn} Q_0(v_m, v_n) + M_k^{mn\alpha\beta} Q_{\alpha\beta} (v_m, v_n) \big) \Big) \Big\|_{L^{6/5}(\mathbb{R}^3)} \\ &\quad\lesssim \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^6(\mathbb{R}^3)}^2 \\ &\quad\lesssim C_2 {\epsilon} t^\delta \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^2}^{2/3} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J {\partial} v \big\|_{L^\infty}^{4/3} \\ &\quad\lesssim C_2 {\epsilon} (C_1 {\epsilon})^2 t^{-4/3 + 2 \delta}, \end{aligned} \end{align*} $$in which we used the estimate in equation (5.12).
Similarly, in order to estimate ![]() $\big \| {\partial }^I L^J V_{n, i} \big \|_{L^2(\mathbb {R}^3)}$, we need to demonstrate that
$\big \| {\partial }^I L^J V_{n, i} \big \|_{L^2(\mathbb {R}^3)}$, we need to demonstrate that
 $$ \begin{align*}\begin{aligned} & \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J \big(M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k) \big) \|_{L^{6/5}(\mathbb{R}^3)} \\ &\quad\lesssim t^{-1} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^3(\mathbb{R}^3)} \\ &\quad\lesssim C_2 {\epsilon} t^{-1 + \delta} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)}^{2/3} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)}^{1/3} \\ &\quad\lesssim C_2 {\epsilon} C_1 {\epsilon} t^{-4/3 + \delta}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} & \sum_{|I| + |J| \leq N-3} \big\| {\partial}^I L^J \big(M_i^{jk\alpha\beta} Q_{\alpha\beta} (v_j, v_k) \big) \|_{L^{6/5}(\mathbb{R}^3)} \\ &\quad\lesssim t^{-1} \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^3(\mathbb{R}^3)} \\ &\quad\lesssim C_2 {\epsilon} t^{-1 + \delta} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)}^{2/3} \sum_{|I| + |J| \leq N-3} \big\| {\partial} {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)}^{1/3} \\ &\quad\lesssim C_2 {\epsilon} C_1 {\epsilon} t^{-4/3 + \delta}. \end{aligned} \end{align*} $$ The estimate for ![]() $\big \| {\partial }^I L^J V_{n, i}^5 \big \|_{L^2(\mathbb {R}^3)}$ with
$\big \| {\partial }^I L^J V_{n, i}^5 \big \|_{L^2(\mathbb {R}^3)}$ with ![]() $|I| + |J| \leq N-2$ is trivial according to Proposition 3.1, since the equation is homogeneous.
$|I| + |J| \leq N-2$ is trivial according to Proposition 3.1, since the equation is homogeneous.
Estimate for ![]() $\big \| {\partial }^I L^J {\partial } V_{n,i}^{\gamma }\big \|_{L^2(\mathbb {R}^3)}$. We utilise the energy estimate for the equation of
$\big \| {\partial }^I L^J {\partial } V_{n,i}^{\gamma }\big \|_{L^2(\mathbb {R}^3)}$. We utilise the energy estimate for the equation of ![]() ${\partial }^I L^J {\partial } V_{n,i}^{\gamma }$ with
${\partial }^I L^J {\partial } V_{n,i}^{\gamma }$ with ![]() $|I| + |J| \leq N-2$ to get
$|I| + |J| \leq N-2$ to get
 $$ \begin{align*}\begin{aligned} E_m (t, {\partial}^I L^J V_{n,i}^{\gamma})^{1/2} &\leq \int_{t_0}^t \big\| {\partial}^I L^J \big( M_i^{jk\gamma\beta} v_j {\partial}_\beta v_k - M_i^{jk\alpha\gamma} v_j {\partial}_\alpha v_k \big) \big\|_{L^2(\mathbb{R}^3)} \, dt' \\ &\lesssim \int_{t_0}^t \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| {\partial} {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \, dt' \\ &\lesssim \int_{t_0}^t C_2 {\epsilon} t^{\prime \delta} C_1 {\epsilon} t^{\prime -1} \, dt' \lesssim C_2 {\epsilon} C_1 {\epsilon} t^\delta. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} E_m (t, {\partial}^I L^J V_{n,i}^{\gamma})^{1/2} &\leq \int_{t_0}^t \big\| {\partial}^I L^J \big( M_i^{jk\gamma\beta} v_j {\partial}_\beta v_k - M_i^{jk\alpha\gamma} v_j {\partial}_\alpha v_k \big) \big\|_{L^2(\mathbb{R}^3)} \, dt' \\ &\lesssim \int_{t_0}^t \sum_{|I| + |J| \leq N-2} \big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \sum_{|I| + |J| \leq N-2} \big\| {\partial} {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \, dt' \\ &\lesssim \int_{t_0}^t C_2 {\epsilon} t^{\prime \delta} C_1 {\epsilon} t^{\prime -1} \, dt' \lesssim C_2 {\epsilon} C_1 {\epsilon} t^\delta. \end{aligned} \end{align*} $$By the definition of ![]() $E_m$ and the commutator estimates, we deduce
$E_m$ and the commutator estimates, we deduce
According to the refined bounds in Proposition 5.4, we easily know that the estimates in equation (5.13) are true for all ![]() $t \in [t_0, + \infty )$ after carefully choosing
$t \in [t_0, + \infty )$ after carefully choosing ![]() $C_2$ large enough and
$C_2$ large enough and ![]() ${\epsilon }$ sufficiently small (we might shrink the choice of
${\epsilon }$ sufficiently small (we might shrink the choice of ![]() ${\epsilon }$ in Proof 4.2 if needed, and nothing else is affected).
${\epsilon }$ in Proof 4.2 if needed, and nothing else is affected).
The Klainerman-Sobolev inequality in equation (2.11) together with equation (5.13) provides the following mass-independent results
 $$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^\delta, \qquad |I| + |J| = N-2, \\ &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^{-1}, \qquad |I| + |J| \leq N-6, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon}, \qquad |I| + |J| \leq N-3, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^\delta, \qquad |I| + |J| = N-2, \\ &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_2 {\epsilon} t^{-1}, \qquad |I| + |J| \leq N-6, \end{aligned} \end{align} $$which are valid for all ![]() $t \in [t_0, +\infty )$.
$t \in [t_0, +\infty )$.
Next, to proceed to prove the bounds of high-order energy in Proposition 5.1, we make new bootstrap assumptions for ![]() $t \in [t_0, t_2)$ (and for all i):
$t \in [t_0, t_2)$ (and for all i):
 $$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_3 {\epsilon}, \qquad |I| + |J| \leq N-1, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_3 {\epsilon}, \qquad |I| + |J| \leq N. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_3 {\epsilon}, \qquad |I| + |J| \leq N-1, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\leq C_3 {\epsilon}, \qquad |I| + |J| \leq N. \end{aligned} \end{align} $$Similar to the definition of ![]() $t_1$,
$t_1$, ![]() $t_2$ is defined by
$t_2$ is defined by
Recall that ![]() $C_3 \geq C_2$ is to be determined.
$C_3 \geq C_2$ is to be determined.
We have the following refined estimates for high-order cases.
Proposition 5.5. Assuming the estimate in equation (5.18) is true, then for all ![]() $t \in [t_0, t_2)$, we have
$t \in [t_0, t_2)$, we have
 $$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_3 {\epsilon})^2, \qquad |I| + |J| \leq N-1, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_3 {\epsilon})^2, \qquad |I| + |J| \leq N. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_3 {\epsilon})^2, \qquad |I| + |J| \leq N-1, \\ \big\| {\partial}^I L^J \big( V_{c, i}, V_{m, i}, V_{n, i}^5 \big) \big\|_{L^2(\mathbb{R}^3)} + t^{-\delta} \big\| {\partial}^I L^J {\partial} V_{n,i}^{\gamma} \big\|_{L^2(\mathbb{R}^3)} &\lesssim {\epsilon} + (C_3 {\epsilon})^2, \qquad |I| + |J| \leq N. \end{aligned} \end{align} $$ The proof for Proposition 5.4 also applies to Proposition 5.5, so we omit it. Also, similarly, we can choose ![]() $C_3$ large enough, and
$C_3$ large enough, and ![]() ${\epsilon }$ sufficiently small (we shrink it further if needed), so that we can improve the estimates in equation (5.18) with a factor
${\epsilon }$ sufficiently small (we shrink it further if needed), so that we can improve the estimates in equation (5.18) with a factor ![]() $1/2$ in front of the original bounds. And this indicates that the estimates in equation (5.18) are valid for all
$1/2$ in front of the original bounds. And this indicates that the estimates in equation (5.18) are valid for all ![]() $t \in [t_0, + \infty )$.
$t \in [t_0, + \infty )$.
The proof for Proposition 5.1 follows from the established estimates in equations (5.13) and (5.18), which are valid for all ![]() $t \in [t_0, +\infty )$.
$t \in [t_0, +\infty )$.
5.3 The mass-independent wave decay for the solution
With the estimates built in Proposition 5.1, we have the following results for the original solution ![]() $v = (v_i)$.
$v = (v_i)$.
Lemma 5.6. For all ![]() $t \in [t_0, +\infty )$, we have
$t \in [t_0, +\infty )$, we have
 $$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_3 {\epsilon}, \qquad |I| + |J| \leq N-1, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^\delta, \qquad |I| + |J| = N. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_3 {\epsilon}, \qquad |I| + |J| \leq N-1, \\ &\big\| {\partial}^I L^J v \big\|_{L^2(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^\delta, \qquad |I| + |J| = N. \end{aligned} \end{align} $$The proof for Lemma 5.6 follows from the proof for Lemma 5.3.
Next, we apply the Klainerman-Sobolev inequality in equation (2.11) to arrive at the mass-independent pointwise decay results.
Proposition 5.7. It holds that
 $$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^{-1}, \qquad |I| + |J| \leq N-4, \\ &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^{-1 + \delta}, \qquad |I| + |J| = N-3. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^{-1}, \qquad |I| + |J| \leq N-4, \\ &\big\| {\partial}^I L^J v \big\|_{L^\infty(\mathbb{R}^3)} \lesssim C_3 {\epsilon} t^{-1 + \delta}, \qquad |I| + |J| = N-3. \end{aligned} \end{align} $$We now establish equation (1.4) in Theorem 1.1.
Proof of equation (1.4).
From Proposition 5.7, we obtain the mass-independent pointwise decay result
while the estimates in Lemma 4.2 give us the mass-dependent Klein-Gordon decay
Combining these two kinds of decay bounds, we are led to
But we see equation (5.23) is obviously true for the case of ![]() $m = 0$ (because it is just the case of wave equations), and hence the proof for equation (1.4) is complete.
$m = 0$ (because it is just the case of wave equations), and hence the proof for equation (1.4) is complete.
6 Proof for the covergence result
With the global existence result and the unified pointwise decay result prepared in the last two sections, we now want to build the convergence result when the mass parameter m goes to 0.
Proof of Theorem 1.2.
We take the difference between the equation of ![]() $v_i^{(m)}$ and the equation of
$v_i^{(m)}$ and the equation of ![]() $v_i^{(0)}$ to have
$v_i^{(0)}$ to have
 $$ \begin{align*}\begin{aligned} &- \Box \big( v_i^{(m)} - v_i^{(0)} \big) + m^2 \big( v_i^{(m)} - v_i^{(0)} \big) \\ &= - m^2 v_i^{(0)} + N^{jk}_i Q_0 \big(v_j^{(m)} - v_j^{(0)}, v_k^{(m)} \big) + N^{jk}_i Q_0 \big(v_j^{(0)}, v_k^{(m)} - v_k^{(0)} \big) \\ &\quad{}+ M^{jk \alpha \beta}_i Q_{\alpha \beta} \big(v_j^{(m)} - v_j^{(0)}, v_k^{(m)} \big) + M^{jk \alpha \beta}_i Q_{\alpha \beta} \big(v_j^{(0)}, v_k^{(m)} - v_k^{(0)} \big) =: F^{(m)}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &- \Box \big( v_i^{(m)} - v_i^{(0)} \big) + m^2 \big( v_i^{(m)} - v_i^{(0)} \big) \\ &= - m^2 v_i^{(0)} + N^{jk}_i Q_0 \big(v_j^{(m)} - v_j^{(0)}, v_k^{(m)} \big) + N^{jk}_i Q_0 \big(v_j^{(0)}, v_k^{(m)} - v_k^{(0)} \big) \\ &\quad{}+ M^{jk \alpha \beta}_i Q_{\alpha \beta} \big(v_j^{(m)} - v_j^{(0)}, v_k^{(m)} \big) + M^{jk \alpha \beta}_i Q_{\alpha \beta} \big(v_j^{(0)}, v_k^{(m)} - v_k^{(0)} \big) =: F^{(m)}, \end{aligned} \end{align*} $$with zero initial data
The vector field ![]() ${\partial }^I L^J$ with
${\partial }^I L^J$ with ![]() $|I| + |J| \leq N-2$ acts on the equation
$|I| + |J| \leq N-2$ acts on the equation ![]() $v_i^{(m)} - v_i^{(0)}$, and then the energy estimates give
$v_i^{(m)} - v_i^{(0)}$, and then the energy estimates give
 $$ \begin{align*}\begin{aligned} E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} &\leq E_m \big(t_0, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} +\int_{t_0}^t \big\| {\partial}^I L^J F^{(m)} \big\|_{L^2(\mathbb{R}^3)} \, dt', \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} &\leq E_m \big(t_0, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} +\int_{t_0}^t \big\| {\partial}^I L^J F^{(m)} \big\|_{L^2(\mathbb{R}^3)} \, dt', \end{aligned} \end{align*} $$and by the fact ![]() $\big | {\partial } {\partial }^I L^J v \big | \lesssim C_1 {\epsilon } t^{-1}$, we further have
$\big | {\partial } {\partial }^I L^J v \big | \lesssim C_1 {\epsilon } t^{-1}$, we further have
 $$ \begin{align*}\begin{aligned} &E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2}\\ &\quad{}\lesssim m^2 C_1 {\epsilon} t + C_1 {\epsilon} \sum_{|I| + |J| \leq N-2} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt'. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2}\\ &\quad{}\lesssim m^2 C_1 {\epsilon} t + C_1 {\epsilon} \sum_{|I| + |J| \leq N-2} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt'. \end{aligned} \end{align*} $$In succession, we apply Gronwall’s inequality to obtain
with C a generic constant.
Thus by choosing ![]() ${\epsilon }$ sufficiently small such that
${\epsilon }$ sufficiently small such that ![]() $C C_1 {\epsilon } \leq \delta /2$, we complete the proof for the cases of
$C C_1 {\epsilon } \leq \delta /2$, we complete the proof for the cases of ![]() $|I| + |J| \leq N-2$.
$|I| + |J| \leq N-2$.
Based on the estimates obtained and the Klainerman-Sobolev inequality in equation (2.11), we obtain
then for ![]() $|I| + |J| \leq N$ with
$|I| + |J| \leq N$ with ![]() $N\geq 6$, we can bound
$N\geq 6$, we can bound
 $$ \begin{align*}\int_{t_0}^t \big\| {\partial}^I L^J F^{(m)} \big\|_{L^2(\mathbb{R}^3)} \, dx \lesssim m^2 C_1 {\epsilon} t^{1+\delta/2} + C_1 {\epsilon} \sum_{|I| + |J| \leq N} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt', \end{align*} $$
$$ \begin{align*}\int_{t_0}^t \big\| {\partial}^I L^J F^{(m)} \big\|_{L^2(\mathbb{R}^3)} \, dx \lesssim m^2 C_1 {\epsilon} t^{1+\delta/2} + C_1 {\epsilon} \sum_{|I| + |J| \leq N} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt', \end{align*} $$which further yields
 $$ \begin{align*}\begin{aligned} &\sum_{|I| + |J| \leq N} E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \\ &\quad\lesssim m^2 C_1 {\epsilon} t^{1+\delta/2} + C_1 {\epsilon} \sum_{|I| + |J| \leq N} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt'. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\sum_{|I| + |J| \leq N} E_m \big(t, {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \\ &\quad\lesssim m^2 C_1 {\epsilon} t^{1+\delta/2} + C_1 {\epsilon} \sum_{|I| + |J| \leq N} \int_{t_0}^t t^{\prime -1} E_m \big(t', {\partial}^I L^J v_i^{(m)} - {\partial}^I L^J v_i^{(0)} \big)^{1/2} \, dt'. \end{aligned} \end{align*} $$Again, Gronwall’s inequality deduces that (by letting ![]() ${\epsilon }$ sufficiently small)
${\epsilon }$ sufficiently small)
Now the proof is complete.
Acknowledgments
The author is grateful to Philippe G. LeFloch (Sorbonne University) for introducing the problem of ‘The vanishing-mass problem for wave–Klein–Gordon systems’ to him and for many discussions. The author also would like to thank Siyuan Ma (Sorbonne University) and Chenmin Sun (University of Cergy-Pontoise) for helpful discussions. The author owes thanks to Xu Yuan (The Chinese University of Hong Kong) for finding typos. The author is grateful to the anonymous referee for valuable comments.
Conflict of Interest
None.
Funding statement
This research was partially supported by the China Postdoctoral Science Foundation, with grant number 2021M690702.