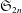Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Im, Mee Seong
and
Zhu, Jieru
2022.
Transitioning Between Tableaux and Spider Bases for Specht Modules.
Algebras and Representation Theory,
Vol. 25,
Issue. 2,
p.
387.
Patrias, Rebecca
Pechenik, Oliver
and
Striker, Jessica
2022.
A web basis of invariant polynomials from noncrossing partitions.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108603.
Kim, Jesse
and
Rhoades, Brendon
2023.
Set Partitions, Fermions, and Skein Relations.
International Mathematics Research Notices,
Vol. 2023,
Issue. 11,
p.
9427.
Hwang, Byung-Hak
Jang, Jihyeug
and
Oh, Jaeseong
2023.
A combinatorial model for the transition matrix between the Specht and -web bases.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Patrias, Rebecca
and
Pechenik, Oliver
2023.
Tableau evacuation and webs.
Proceedings of the American Mathematical Society, Series B,
Vol. 10,
Issue. 30,
p.
341.
Heard, Samuel David
and
Kujawa, Jonathan R
2023.
Positivity and Web Bases for Specht Modules of Hecke Algebras.
International Mathematics Research Notices,