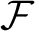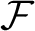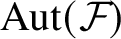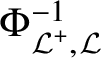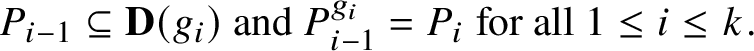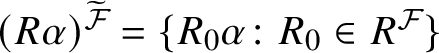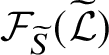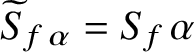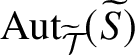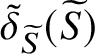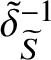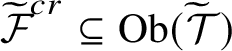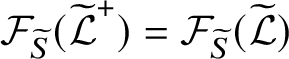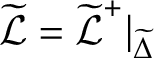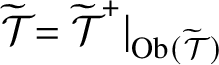1. Introduction
Given a finite group G with a Sylow p-subgroup S, the fusion system
![]() $\mathcal {F}_S(G)$
is the category whose objects are the subgroups of S and whose morphisms are the injective group homomorphisms induced by conjugation in G. It turns out that the fusion system
$\mathcal {F}_S(G)$
is the category whose objects are the subgroups of S and whose morphisms are the injective group homomorphisms induced by conjugation in G. It turns out that the fusion system
![]() $\mathcal {F}_S(G)$
determines the p-completed classifying space
$\mathcal {F}_S(G)$
determines the p-completed classifying space
![]() $BG^\wedge _p$
up to homotopy; this statement is known as the Martino–Priddy conjecture and was first proved by Oliver [Reference Oliver17, Reference Oliver18]. Fusion systems also play an important role in many other contexts; for example, in a program announced by Aschbacher to revisit the classification of finite simple groups. The concept of a saturated fusion system generalises the properties of
$BG^\wedge _p$
up to homotopy; this statement is known as the Martino–Priddy conjecture and was first proved by Oliver [Reference Oliver17, Reference Oliver18]. Fusion systems also play an important role in many other contexts; for example, in a program announced by Aschbacher to revisit the classification of finite simple groups. The concept of a saturated fusion system generalises the properties of
![]() $\mathcal {F}_S(G)$
. In particular, a saturated fusion system is a category
$\mathcal {F}_S(G)$
. In particular, a saturated fusion system is a category
![]() $\mathcal {F}$
that comes equipped with a p-group S such that the objects of
$\mathcal {F}$
that comes equipped with a p-group S such that the objects of
![]() $\mathcal {F}$
are the subgroups of S and the morphism sets consist of injective group homomorphisms subject to certain axioms.
$\mathcal {F}$
are the subgroups of S and the morphism sets consist of injective group homomorphisms subject to certain axioms.
For the purposes of homotopy theory, Broto, Levi and Oliver Reference Broto, Levi and Oliver[3] defined centric linking systems associated to saturated fusion systems. A category
![]() $\mathcal L_S^c(G)$
, which is a centric linking system associated to
$\mathcal L_S^c(G)$
, which is a centric linking system associated to
![]() $\mathcal {F}_S(G)$
, can be constructed directly from the group G. The p-completed classifying space
$\mathcal {F}_S(G)$
, can be constructed directly from the group G. The p-completed classifying space
![]() $BG^\wedge _p$
of G is homotopy equivalent to the p-completed nerve of the category
$BG^\wedge _p$
of G is homotopy equivalent to the p-completed nerve of the category
![]() $\mathcal L_S^c(G)$
. This fact played an important role in the proof of the Martino–Priddy conjecture. In the abstract context, there is an essentially unique centric linking system associated to every saturated fusion system. This long-standing conjecture was proved by Chermak Reference Chermak[6] and subsequently by Oliver Reference Oliver[20]. Both proofs depend a priori on the classification of finite simple groups, but work of Glauberman–Lynd Reference Glauberman and Lynd[11] removes the dependence of Oliver’s proof on the classification.
$\mathcal L_S^c(G)$
. This fact played an important role in the proof of the Martino–Priddy conjecture. In the abstract context, there is an essentially unique centric linking system associated to every saturated fusion system. This long-standing conjecture was proved by Chermak Reference Chermak[6] and subsequently by Oliver Reference Oliver[20]. Both proofs depend a priori on the classification of finite simple groups, but work of Glauberman–Lynd Reference Glauberman and Lynd[11] removes the dependence of Oliver’s proof on the classification.
Linking systems not only form the algebraic foundation for defining p-completed classifying spaces of fusion systems but are also important when studying extensions of fusion systems. The object set of a centric linking system associated to a fusion system
![]() $\mathcal {F}$
over S is a certain set of subgroups of S determined by
$\mathcal {F}$
over S is a certain set of subgroups of S determined by
![]() $\mathcal {F}$
. When studying extensions, one often wants to choose the object sets of linking systems more flexibly. At least partly for that reason, a more general notion of linking systems was introduced by Oliver Reference Oliver[19] (building on earlier work of Broto et al. Reference Broto, Castellana, Grodal, Levi and Oliver[4]). Linking systems are special cases of transporter systems as defined by Oliver and Ventura Reference Oliver and Ventura[21]. Extensions of linking systems and transporter systems were studied, for example, in Reference Andersen, Oliver and Ventura[2], Reference Broto, Castellana, Grodal, Levi and Oliver[5], Reference Oliver and Ventura[21] and Reference Oliver[19].
$\mathcal {F}$
. When studying extensions, one often wants to choose the object sets of linking systems more flexibly. At least partly for that reason, a more general notion of linking systems was introduced by Oliver Reference Oliver[19] (building on earlier work of Broto et al. Reference Broto, Castellana, Grodal, Levi and Oliver[4]). Linking systems are special cases of transporter systems as defined by Oliver and Ventura Reference Oliver and Ventura[21]. Extensions of linking systems and transporter systems were studied, for example, in Reference Andersen, Oliver and Ventura[2], Reference Broto, Castellana, Grodal, Levi and Oliver[5], Reference Oliver and Ventura[21] and Reference Oliver[19].
Chermak Reference Chermak[6] introduced with localities group-like structures that correspond to transporter systems in a certain way. A locality consists more precisely of a ‘partial group’
![]() $\mathcal L$
(i.e., a set
$\mathcal L$
(i.e., a set
![]() $\mathcal L$
with a ‘product’ defined on some tuples of elements of
$\mathcal L$
with a ‘product’ defined on some tuples of elements of
![]() $\mathcal L$
subject to group-like axioms), a ‘Sylow p-subgroup’ S of
$\mathcal L$
subject to group-like axioms), a ‘Sylow p-subgroup’ S of
![]() $\mathcal L$
and a set
$\mathcal L$
and a set
![]() $\Delta $
of subgroups of S (cf. Definitions 2.1 and 2.5). Here
$\Delta $
of subgroups of S (cf. Definitions 2.1 and 2.5). Here
![]() $\Delta $
is called the set of objects of
$\Delta $
is called the set of objects of
![]() $\mathcal L$
and turns out to be the object set of the transporter system corresponding to
$\mathcal L$
and turns out to be the object set of the transporter system corresponding to
![]() $(\mathcal L,\Delta ,S)$
. A rich theory of localities akin to the local theory of finite groups was developed by Chermak [Reference Chermak7, Reference Chermak8, Reference Chermak9]. Extensions of partial groups and localities were studied by Gonzalez Reference Gonzalez[13] and are also the subject of work in progress by Valentina Grazian and the author of this article. At least with the currently known conceptual framework, it seems in fact that there are some advantages to studying extensions of localities rather than extensions of linking systems or transporter systems. For example, for partial groups, there are natural notions of homomorphisms and of partial normal subgroups such that the kernels of the homomorphisms from a locality
$(\mathcal L,\Delta ,S)$
. A rich theory of localities akin to the local theory of finite groups was developed by Chermak [Reference Chermak7, Reference Chermak8, Reference Chermak9]. Extensions of partial groups and localities were studied by Gonzalez Reference Gonzalez[13] and are also the subject of work in progress by Valentina Grazian and the author of this article. At least with the currently known conceptual framework, it seems in fact that there are some advantages to studying extensions of localities rather than extensions of linking systems or transporter systems. For example, for partial groups, there are natural notions of homomorphisms and of partial normal subgroups such that the kernels of the homomorphisms from a locality
![]() $\mathcal L$
are precisely the partial normal subgroups of
$\mathcal L$
are precisely the partial normal subgroups of
![]() $\mathcal L$
.
$\mathcal L$
.
The author of this article Reference Henke[14] suggested a definition of a linking system that is significantly more general than the previously existing notion, and this leads to the corresponding concept of a linking locality (also called a proper locality by Chermak [Reference Chermak8, Reference Chermak9]). It is one of the purposes of this article to prove in this more general context some results that are known to hold for linking systems in Oliver’s definition [Reference Oliver19, Definition 3]. Another purpose of this article is to prove a lemma about homomorphisms between localities (Lemma 3.1) and to reprove in Theorem C a result of Chermak [Reference Chermak8, Theorem A2]. Both Lemma 3.1 and Theorem C are used in joint work of Chermak and the author of this article Reference Chermak and Henke[10] to show that there is a one-to-one correspondence between the normal subsystems of a fusion system and the partial normal subgroups of an associated linking locality. The theorems on linking localities proved in the present article were also used in Reference Henke[15], where the results from Reference Chermak[9] are revisited and extended.
We will now explain our main results in more detail. When studying extensions of linking systems or linking localities, their automorphism groups play an important role. Thus, it is of interest to see that different linking systems or linking localities associated to the same fusion system
![]() $\mathcal {F}$
have the same automorphism group. This is indeed the case if we consider linking systems and linking localities with
$\mathcal {F}$
have the same automorphism group. This is indeed the case if we consider linking systems and linking localities with
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant object sets, as, for example, the typically used sets of
$\mathrm {Aut}(\mathcal {F})$
-invariant object sets, as, for example, the typically used sets of
![]() $\mathcal {F}$
-centric,
$\mathcal {F}$
-centric,
![]() $\mathcal {F}$
-quasicentric or
$\mathcal {F}$
-quasicentric or
![]() $\mathcal {F}$
-subcentric subgroups. For linking localities, we prove the following theorem. In Theorem 5.1 and Theorem 5.3 we also prove some more general statements about isomorphisms and automorphisms of linking localities.
$\mathcal {F}$
-subcentric subgroups. For linking localities, we prove the following theorem. In Theorem 5.1 and Theorem 5.3 we also prove some more general statements about isomorphisms and automorphisms of linking localities.
Theorem A.1. Let
![]() $\mathcal {F}$
be a saturated fusion system over S. If
$\mathcal {F}$
be a saturated fusion system over S. If
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
are linking localities over
$(\mathcal L^+,\Delta ^+,S)$
are linking localities over
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^+$
are
$\Delta ^+$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then
$\mathrm {Aut}(\mathcal {F})$
-invariant, then
![]() $\mathrm {Aut}(\mathcal L,\Delta ,S)\cong \mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
. In the case that
$\mathrm {Aut}(\mathcal L,\Delta ,S)\cong \mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
. In the case that
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
, a group isomorphism is given by
$\mathcal L=\mathcal L^+|_\Delta $
, a group isomorphism is given by
The reader is referred to Definition 2.22 for the definition of the ‘restriction’
![]() $\mathcal L^+|_\Delta $
. The above-mentioned correspondence between transporter systems and localities (which we outline in Subsection 4.2) leads to a correspondence between linking systems and linking localities. Passing to the restriction
$\mathcal L^+|_\Delta $
. The above-mentioned correspondence between transporter systems and localities (which we outline in Subsection 4.2) leads to a correspondence between linking systems and linking localities. Passing to the restriction
![]() $\mathcal L^+|_\Delta $
corresponds in the world of transporter systems to passing to the full subcategory with object set
$\mathcal L^+|_\Delta $
corresponds in the world of transporter systems to passing to the full subcategory with object set
![]() $\Delta $
. Thus, we obtain the following theorem for linking systems.
$\Delta $
. Thus, we obtain the following theorem for linking systems.
Theorem A.2. Suppose that
![]() $\mathcal {F}$
is a saturated fusion system. If
$\mathcal {F}$
is a saturated fusion system. If
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
are linking systems associated to the same saturated fusion system
$\mathcal {T}^{\;+}$
are linking systems associated to the same saturated fusion system
![]() $\mathcal {F}$
such that the object sets of
$\mathcal {F}$
such that the object sets of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
are
$\mathcal {T}^{\;+}$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then
$\mathrm {Aut}(\mathcal {F})$
-invariant, then
![]() $\mathrm {Aut}(\mathcal {T}\;)\cong \mathrm {Aut}(\mathcal {T}^{\;+})$
. In the case that
$\mathrm {Aut}(\mathcal {T}\;)\cong \mathrm {Aut}(\mathcal {T}^{\;+})$
. In the case that
![]() $\mathcal {T}$
is a full subcategory of
$\mathcal {T}$
is a full subcategory of
![]() $\mathcal {T}^{\;+}$
, a group isomorphism
$\mathcal {T}^{\;+}$
, a group isomorphism
![]() $\mathrm {Aut}(\mathcal {T}^{\;+})\longrightarrow \mathrm {Aut}(\mathcal {T}\;)$
is given by restriction.
$\mathrm {Aut}(\mathcal {T}^{\;+})\longrightarrow \mathrm {Aut}(\mathcal {T}\;)$
is given by restriction.
By
![]() $\mathrm {Aut}(\mathcal {T}\;)$
we mean here the group of isotypical self-equivalences of
$\mathrm {Aut}(\mathcal {T}\;)$
we mean here the group of isotypical self-equivalences of
![]() $\mathcal {T}$
that send inclusions to inclusions; see Definition 4.1. In the literature,
$\mathcal {T}$
that send inclusions to inclusions; see Definition 4.1. In the literature,
![]() $\mathrm {Aut}(\mathcal {T}\;)$
is often denoted by
$\mathrm {Aut}(\mathcal {T}\;)$
is often denoted by
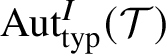 $\mathrm {Aut}_{\operatorname {typ}}^I(\mathcal {T}\;)$
. We emphasise also that the term linking system refers to a linking system in the general sense of Reference Henke[14] (cf. Definition 4.7). A version of Theorem A.2 was proved before by Andersen, Oliver and Ventura [Reference Andersen, Oliver and Ventura2, Lemma 1.17] for linking systems in Oliver’s definition; that is, for linking systems whose objects are quasicentric subgroups. The precise statement is actually given for outer automorphism groups of linking systems. We formulate a similar result in Theorem 5.5. For this purpose, we state in Lemma 4.10 that, for any linking system
$\mathrm {Aut}_{\operatorname {typ}}^I(\mathcal {T}\;)$
. We emphasise also that the term linking system refers to a linking system in the general sense of Reference Henke[14] (cf. Definition 4.7). A version of Theorem A.2 was proved before by Andersen, Oliver and Ventura [Reference Andersen, Oliver and Ventura2, Lemma 1.17] for linking systems in Oliver’s definition; that is, for linking systems whose objects are quasicentric subgroups. The precise statement is actually given for outer automorphism groups of linking systems. We formulate a similar result in Theorem 5.5. For this purpose, we state in Lemma 4.10 that, for any linking system
![]() $\mathcal {T}$
associated to a saturated fusion system
$\mathcal {T}$
associated to a saturated fusion system
![]() $\mathcal {F}$
, there is an exact sequence
$\mathcal {F}$
, there is an exact sequence
 $$ \begin{align*}1\longrightarrow Z(\mathcal{F}\;)\xrightarrow{\;\;\delta_S\;\;} \mathrm{Aut}_{\mathcal{T}}\;(S)\longrightarrow \mathrm{Aut}(\mathcal{T}\;)\longrightarrow \mathrm{Out}_{{\operatorname{typ}}}(\mathcal{T}\;)\longrightarrow 1. \end{align*} $$
$$ \begin{align*}1\longrightarrow Z(\mathcal{F}\;)\xrightarrow{\;\;\delta_S\;\;} \mathrm{Aut}_{\mathcal{T}}\;(S)\longrightarrow \mathrm{Aut}(\mathcal{T}\;)\longrightarrow \mathrm{Out}_{{\operatorname{typ}}}(\mathcal{T}\;)\longrightarrow 1. \end{align*} $$
Again, this was known to be true for linking systems in Oliver’s definition (cf. [Reference Andersen, Oliver and Ventura2, Lemma 1.14(a)]) and the proof of the more general statement is given by similar arguments.
Theorem 5.5 allows us to prove the following theorem from the corresponding statement for centric linking systems, which was shown by Broto, Levi and Oliver [Reference Broto, Levi and Oliver3, Theorem 8.1]. The statement was also known before for linking systems in Oliver’s definition; see [Reference Aschbacher, Kessar and Oliver1, Theorem 4.22]. For any space X,
![]() $\mathrm {Out}(X)$
denotes the group of homotopy classes of self-equivalences of X.
$\mathrm {Out}(X)$
denotes the group of homotopy classes of self-equivalences of X.
Theorem B. Let
![]() $\mathcal {T}$
be a linking system associated to a saturated fusion system
$\mathcal {T}$
be a linking system associated to a saturated fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)$
is
$\mathrm {Ob}(\mathcal {T}\;)$
is
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant. Then there is an isomorphism
$\mathrm {Aut}(\mathcal {F})$
-invariant. Then there is an isomorphism
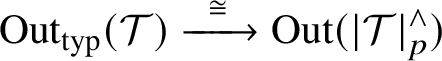 $$ \begin{align*}\mathrm{Out}_{\operatorname{typ}}(\mathcal{T}\;)\xrightarrow{\;\;\cong\;\;} \mathrm{Out}(|\mathcal{T}\;|^\wedge_p)\end{align*} $$
$$ \begin{align*}\mathrm{Out}_{\operatorname{typ}}(\mathcal{T}\;)\xrightarrow{\;\;\cong\;\;} \mathrm{Out}(|\mathcal{T}\;|^\wedge_p)\end{align*} $$
that sends the class of
![]() $\alpha \in \mathrm {Aut}(\mathcal {T}\;)$
to
$\alpha \in \mathrm {Aut}(\mathcal {T}\;)$
to
![]() $|\alpha |^\wedge _p\colon |\mathcal {T}\;|^\wedge _p\rightarrow |\mathcal {T}\;|^\wedge _p$
.
$|\alpha |^\wedge _p\colon |\mathcal {T}\;|^\wedge _p\rightarrow |\mathcal {T}\;|^\wedge _p$
.
We show Theorem A.2 and some more general theorems about isomorphisms and automorphisms of linking systems (Theorems 5.2 and 5.4) from the corresponding statements for linking localities via the one-to-one correspondence between localities and transporter systems. However, in Remark 5.6, we outline how a direct proof could be given via similar arguments as in [Reference Andersen, Oliver and Ventura2, Lemma 1.17]. The crucial point in each of the proofs of Theorems A.1 and A.2 is to show that the appropriate restriction map is surjective. The necessary argument for localities is similar to the argument for transporter systems in [Reference Andersen, Oliver and Ventura2, Lemma 1.17], but it can be formulated in a very general way such that it becomes useful in other contexts. Namely, in Lemma 3.1 we show that, under certain assumptions, a homomorphism from a locality
![]() $(\mathcal L,\Delta ,S)$
can be extended to a homomorphism from a locality
$(\mathcal L,\Delta ,S)$
can be extended to a homomorphism from a locality
![]() $(\mathcal L^+,\Delta ^+,S)$
with
$(\mathcal L^+,\Delta ^+,S)$
with
![]() $\mathcal L^+|_\Delta =\mathcal L$
. We use Lemma 3.1 to give a new proof of [Reference Chermak8, Theorem A2] (stated as Theorem C(a) in this article) in Section 6. Moreover, both Lemma 3.1 and Theorem C are used in Reference Chermak and Henke[10]. For any partial group
$\mathcal L^+|_\Delta =\mathcal L$
. We use Lemma 3.1 to give a new proof of [Reference Chermak8, Theorem A2] (stated as Theorem C(a) in this article) in Section 6. Moreover, both Lemma 3.1 and Theorem C are used in Reference Chermak and Henke[10]. For any partial group
![]() $\mathcal L$
, we denote by
$\mathcal L$
, we denote by
![]() ${\mathfrak {N}}(\mathcal L)$
the set of partial normal subgroups of
${\mathfrak {N}}(\mathcal L)$
the set of partial normal subgroups of
![]() $\mathcal L$
.
$\mathcal L$
.
Theorem C. If
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
![]() $\mathcal {F}$
with
$\mathcal {F}$
with
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
, then the following hold:
$\mathcal L=\mathcal L^+|_\Delta $
, then the following hold:
-
(a) The map
is well defined and bijective. Both $$ \begin{align*}\Phi_{\mathcal L^+,\mathcal L}\colon{\mathfrak{N}}(\mathcal L^+)\longrightarrow {\mathfrak{N}}(\mathcal L),\;\mathcal{N}^+\mapsto \mathcal{N}^+\cap\mathcal L\end{align*} $$
$$ \begin{align*}\Phi_{\mathcal L^+,\mathcal L}\colon{\mathfrak{N}}(\mathcal L^+)\longrightarrow {\mathfrak{N}}(\mathcal L),\;\mathcal{N}^+\mapsto \mathcal{N}^+\cap\mathcal L\end{align*} $$
 $\Phi _{\mathcal L^+,\mathcal L}$
and
$\Phi _{\mathcal L^+,\mathcal L}$
and
 $\Phi _{\mathcal L^+,\mathcal L}^{-1}$
are inclusion preserving.
$\Phi _{\mathcal L^+,\mathcal L}^{-1}$
are inclusion preserving.
-
(b) If
 $\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
and
$\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
and
 $\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
such that
$\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
such that
 $\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
$\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
 $\mathcal {F}$
-invariant, then
$\mathcal {F}$
-invariant, then
 $\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
.
$\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
. -
(c) Let
 $\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L)$
, set
$\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L)$
, set
 $\mathcal {N}:=\mathcal {N}^+\cap \mathcal L$
,
$\mathcal {N}:=\mathcal {N}^+\cap \mathcal L$
,
 $\mathcal {K}:=\mathcal {K}^+\cap \mathcal L$
and
$\mathcal {K}:=\mathcal {K}^+\cap \mathcal L$
and
 $T:=\mathcal {N}^+\cap S=\mathcal {N}\cap S$
. Then
$T:=\mathcal {N}^+\cap S=\mathcal {N}\cap S$
. Then
 $\mathcal {N}=\mathcal {K} T$
if and only if
$\mathcal {N}=\mathcal {K} T$
if and only if
 $\mathcal {N}^+=\mathcal {K}^+ T$
.
$\mathcal {N}^+=\mathcal {K}^+ T$
.
The statement in part (a) of the above theorem that
![]() $\Phi _{\mathcal L,\mathcal L^+}$
and its inverse are inclusion preserving is equivalent to saying that every
$\Phi _{\mathcal L,\mathcal L^+}$
and its inverse are inclusion preserving is equivalent to saying that every
![]() $\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
is the smallest partial normal subgroup of
$\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
is the smallest partial normal subgroup of
![]() $\mathcal L^+$
containing
$\mathcal L^+$
containing
![]() $\mathcal {N}^+\cap \mathcal L$
. As a corollary to Theorem C(a) one can also show that any two linking localities over the same fusion system have the same number of partial normal subgroups; see Corollary 6.4.
$\mathcal {N}^+\cap \mathcal L$
. As a corollary to Theorem C(a) one can also show that any two linking localities over the same fusion system have the same number of partial normal subgroups; see Corollary 6.4.
In his original proof of Theorem C(a), Chermak went into the (somewhat complicated) details of the construction of elementary expansions as introduced in [Reference Chermak6, Section 5]. Applying Lemma 3.1 makes this unnecessary in our new proof. We do, however, use [Reference Chermak6, Theorem 5.14], which is proved via elementary expansions. Theorem C(c) fills in a small gap in the proof of [Reference Chermak8, Lemma 7.3].
Organization of the article. After introducing some background in Section 2, we prove Lemma 3.1, which is used in the proofs of our main results. Theorems A.1 and A.2 together with some more general theorems and with Theorem B are proved in Section 5. In preparation for that, in Section 4 we define automorphisms and isomorphisms of transporter systems (cf. Definition 4.1). Moreover, we explain the correspondence between localities and transporter systems, which is then used in Section 5 to prove theorems about linking systems from corresponding statements about linking localities. Finally, in Section 6, we prove Theorem C. The proof of Theorem C is independent of the results stated and proved in Sections 4 and 5.
2. Localities and fusion systems
In this section we will introduce some basic definitions and show some lemmas needed in the proofs of our main theorems. The reader is referred to Reference Aschbacher, Kessar and Oliver[1] for background on fusion systems and to Reference Chermak[6] and Reference Chermak[7] for a more comprehensive introduction to localities. We will, however, summarise the most important definitions and results concerning localities. In particular, we will recall the definitions of homomorphisms, projections, isomorphisms and automorphisms of localities in Subsection 2.5. Some background on morphisms of fusion systems is also provided in Subsection 2.4.
2.1. Partial groups
For any set
![]() $\mathcal {M}$
, write
$\mathcal {M}$
, write
![]() $\mathbf {W}(\mathcal {M})$
for the set of words in
$\mathbf {W}(\mathcal {M})$
for the set of words in
![]() $\mathcal {M}$
. If
$\mathcal {M}$
. If
![]() $u,v\in \mathbf {W}(\mathcal {M})$
, then
$u,v\in \mathbf {W}(\mathcal {M})$
, then
![]() $u \circ v$
denotes the concatenation of the two words. The empty word will be denoted by
$u \circ v$
denotes the concatenation of the two words. The empty word will be denoted by
![]() $\emptyset $
.
$\emptyset $
.
Definition 2.1 Partial Group
Let
![]() $\mathcal L$
be a nonempty set, let
$\mathcal L$
be a nonempty set, let
![]() $\mathbf {D}$
be a subset of
$\mathbf {D}$
be a subset of
![]() $\mathbf {W}(\mathcal L)$
, let
$\mathbf {W}(\mathcal L)$
, let
![]() $\Pi \colon \mathbf {D} \longrightarrow \mathcal L$
be a map and let
$\Pi \colon \mathbf {D} \longrightarrow \mathcal L$
be a map and let
![]() $(-)^{-1} \colon \mathcal L \longrightarrow \mathcal L$
be an involutory bijection, which we extend to a map
$(-)^{-1} \colon \mathcal L \longrightarrow \mathcal L$
be an involutory bijection, which we extend to a map
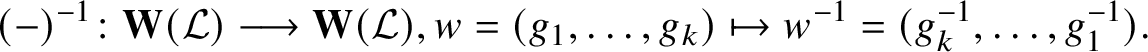 $$ \begin{align*}(-)^{-1} \colon \mathbf{W}(\mathcal L) \longrightarrow \mathbf{W}(\mathcal L), w = (g_1, \dots, g_k) \mapsto w^{-1} = (g_k^{-1}, \dots, g_1^{-1}).\\[-15pt]\end{align*} $$
$$ \begin{align*}(-)^{-1} \colon \mathbf{W}(\mathcal L) \longrightarrow \mathbf{W}(\mathcal L), w = (g_1, \dots, g_k) \mapsto w^{-1} = (g_k^{-1}, \dots, g_1^{-1}).\\[-15pt]\end{align*} $$
We say that
![]() $\mathcal L$
is a partial group with product
$\mathcal L$
is a partial group with product
![]() $\Pi $
and inversion
$\Pi $
and inversion
![]() $(-)^{-1}$
if the following hold:
$(-)^{-1}$
if the following hold:
-
(PG1)
 $\mathcal L \subseteq \mathbf {D}$
(i.e.,
$\mathcal L \subseteq \mathbf {D}$
(i.e.,
 $\mathbf {D}$
contains all words of length 1), and (So, in particular,
$\mathbf {D}$
contains all words of length 1), and (So, in particular, $$ \begin{align*} u \circ v \in \mathbf{D} \Rightarrow u,v \in \mathbf{D}.\\[-15pt]\end{align*} $$
$$ \begin{align*} u \circ v \in \mathbf{D} \Rightarrow u,v \in \mathbf{D}.\\[-15pt]\end{align*} $$
 $\emptyset \in \mathbf {D}$
.)
$\emptyset \in \mathbf {D}$
.)
-
(PG2)
 $\Pi $
restricts to the identity map on
$\Pi $
restricts to the identity map on
 $\mathcal L$
.
$\mathcal L$
. -
(PG3)
 $u \circ v \circ w \in \mathbf {D} \Rightarrow u \circ (\Pi (v)) \circ w \in \mathbf {D}$
, and
$u \circ v \circ w \in \mathbf {D} \Rightarrow u \circ (\Pi (v)) \circ w \in \mathbf {D}$
, and
 $\Pi (u \circ v \circ w) = \Pi (u \circ (\Pi (v)) \circ w)$
.
$\Pi (u \circ v \circ w) = \Pi (u \circ (\Pi (v)) \circ w)$
. -
(PG4)
 $w \in \mathbf {D} \Rightarrow w^{-1} \circ w\in \mathbf {D}$
and
$w \in \mathbf {D} \Rightarrow w^{-1} \circ w\in \mathbf {D}$
and
 $\Pi (w^{-1} \circ w) = \operatorname {\mathbf {1}}$
where
$\Pi (w^{-1} \circ w) = \operatorname {\mathbf {1}}$
where
 $\operatorname {\mathbf {1}}:=\Pi (\emptyset )$
.
$\operatorname {\mathbf {1}}:=\Pi (\emptyset )$
.
Note that any group G can be regarded as a partial group with product defined on
![]() $\mathbf {D}=\mathbf {W}(G)$
by extending the ‘binary’ product to a map
$\mathbf {D}=\mathbf {W}(G)$
by extending the ‘binary’ product to a map
If
![]() $\mathcal L$
is a partial group with product
$\mathcal L$
is a partial group with product
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
![]() $u=(f_1,f_2,\dots ,f_n)\in \mathbf {D}$
, then we write also
$u=(f_1,f_2,\dots ,f_n)\in \mathbf {D}$
, then we write also
![]() $f_1f_2\cdots f_n$
for
$f_1f_2\cdots f_n$
for
![]() $\Pi (u)$
.
$\Pi (u)$
.
Lemma 2.2. Let
![]() $\mathcal L$
be a partial group with product
$\mathcal L$
be a partial group with product
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
.
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
.
-
(a) If
 $u,v\in \mathbf {W}(\mathcal L)$
with
$u,v\in \mathbf {W}(\mathcal L)$
with
 $u\circ (\operatorname {\mathbf {1}})\circ v\in \mathbf {D}$
, then
$u\circ (\operatorname {\mathbf {1}})\circ v\in \mathbf {D}$
, then
 $u\circ v\in \mathbf {D}$
and
$u\circ v\in \mathbf {D}$
and
 $\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)=\Pi (u\circ v)$
.
$\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)=\Pi (u\circ v)$
. -
(b) If
 $u,v,w\in \mathbf {W}(\mathcal L)$
such that
$u,v,w\in \mathbf {W}(\mathcal L)$
such that
 $u\circ v\circ v^{-1}\circ w\in \mathbf {D}$
, then
$u\circ v\circ v^{-1}\circ w\in \mathbf {D}$
, then
 $u\circ w\in \mathbf {D}$
and
$u\circ w\in \mathbf {D}$
and
 $\Pi (u\circ v\circ v^{-1}\circ w)=\Pi (u\circ w)$
.
$\Pi (u\circ v\circ v^{-1}\circ w)=\Pi (u\circ w)$
.
Proof. Let
![]() $u,v$
as in (a). If
$u,v$
as in (a). If
![]() $u=v=\emptyset $
, then by axiom (PG1)
$u=v=\emptyset $
, then by axiom (PG1)
![]() $u\circ v=\emptyset \in \mathbf {D}$
, and by axiom (PG2) and the definition of
$u\circ v=\emptyset \in \mathbf {D}$
, and by axiom (PG2) and the definition of
![]() $\operatorname {\mathbf {1}}$
we have
$\operatorname {\mathbf {1}}$
we have
![]() $\Pi (u\circ v)=\Pi (\emptyset )=\operatorname {\mathbf {1}}=\Pi (\operatorname {\mathbf {1}})=\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)$
. So to prove (a), we may assume that
$\Pi (u\circ v)=\Pi (\emptyset )=\operatorname {\mathbf {1}}=\Pi (\operatorname {\mathbf {1}})=\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)$
. So to prove (a), we may assume that
![]() $u\neq \emptyset $
or
$u\neq \emptyset $
or
![]() $v\neq \emptyset $
.
$v\neq \emptyset $
.
For any element
![]() $f\in \mathcal L$
, axiom (PG1) gives
$f\in \mathcal L$
, axiom (PG1) gives
![]() $f=(f)\circ \emptyset \in \mathbf {D}$
. So by axioms (PG2) and (PG3) we have
$f=(f)\circ \emptyset \in \mathbf {D}$
. So by axioms (PG2) and (PG3) we have
![]() $(f,\operatorname {\mathbf {1}})=(f)\circ (\Pi (\emptyset ))\in \mathbf {D}$
and
$(f,\operatorname {\mathbf {1}})=(f)\circ (\Pi (\emptyset ))\in \mathbf {D}$
and
![]() $f=\Pi (f)=\Pi ((f)\circ (\Pi (\emptyset )))=\Pi (f,\operatorname {\mathbf {1}})$
. So if
$f=\Pi (f)=\Pi ((f)\circ (\Pi (\emptyset )))=\Pi (f,\operatorname {\mathbf {1}})$
. So if
![]() $u=(f_1,\dots ,f_n)\neq \emptyset $
, then
$u=(f_1,\dots ,f_n)\neq \emptyset $
, then
![]() $u\circ (\operatorname {\mathbf {1}})\circ v=(f_1,\dots ,f_{n-1})\circ (f_n,\operatorname {\mathbf {1}})\circ v\in \mathbf {D}$
implies by axiom (PG3) that
$u\circ (\operatorname {\mathbf {1}})\circ v=(f_1,\dots ,f_{n-1})\circ (f_n,\operatorname {\mathbf {1}})\circ v\in \mathbf {D}$
implies by axiom (PG3) that
![]() $u\circ v=(f_1,\dots ,f_{n-1})\circ (\Pi (f_n,\operatorname {\mathbf {1}}))\circ v\in \mathbf {D}$
and
$u\circ v=(f_1,\dots ,f_{n-1})\circ (\Pi (f_n,\operatorname {\mathbf {1}}))\circ v\in \mathbf {D}$
and
![]() $\Pi (u\circ v)=\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)$
. So (a) holds in this case. A similar argument shows (a) in the case that
$\Pi (u\circ v)=\Pi (u\circ (\operatorname {\mathbf {1}})\circ v)$
. So (a) holds in this case. A similar argument shows (a) in the case that
![]() $v\neq \emptyset $
.
$v\neq \emptyset $
.
For the proof of (b), let now
![]() $u,v,w\in \mathbf {W}(\mathcal L)$
be arbitrary such that
$u,v,w\in \mathbf {W}(\mathcal L)$
be arbitrary such that
![]() $u\circ v\circ v^{-1}\circ w\in \mathbf {D}$
. Then by axiom (PG3), we have
$u\circ v\circ v^{-1}\circ w\in \mathbf {D}$
. Then by axiom (PG3), we have
![]() $u\circ (\operatorname {\mathbf {1}})\circ w=u\circ (\Pi (v\circ v^{-1}))\circ w\in \mathbf {D}$
and
$u\circ (\operatorname {\mathbf {1}})\circ w=u\circ (\Pi (v\circ v^{-1}))\circ w\in \mathbf {D}$
and
![]() $\Pi (u\circ v\circ v^{-1}\circ w)=\Pi (u\circ (\operatorname {\mathbf {1}})\circ w)$
. Hence, (b) follows from (a).
$\Pi (u\circ v\circ v^{-1}\circ w)=\Pi (u\circ (\operatorname {\mathbf {1}})\circ w)$
. Hence, (b) follows from (a).
Definition 2.3. Let
![]() $\mathcal L$
be a partial group with product
$\mathcal L$
be a partial group with product
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
.
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
.
-
• For every
 $g\in \mathcal L$
we define The map
$g\in \mathcal L$
we define The map $$ \begin{align*} \mathbf{D}(g) = \{ x\in \mathcal L \mid (g^{-1}, x, g) \in \mathbf{D}\}.\\[-15pt] \end{align*} $$
$$ \begin{align*} \mathbf{D}(g) = \{ x\in \mathcal L \mid (g^{-1}, x, g) \in \mathbf{D}\}.\\[-15pt] \end{align*} $$
 $c_g \colon \mathbf {D}(g) \longrightarrow \mathcal L$
,
$c_g \colon \mathbf {D}(g) \longrightarrow \mathcal L$
,
 $x \mapsto x^g = \Pi (g^{-1}, x, g)$
is the conjugation map by g.
$x \mapsto x^g = \Pi (g^{-1}, x, g)$
is the conjugation map by g.
-
• If
 $\mathcal H$
is a subset of
$\mathcal H$
is a subset of
 $\mathcal L$
and
$\mathcal L$
and
 $\mathcal H \subseteq \mathbf {D}(g)$
, then we set
$\mathcal H \subseteq \mathbf {D}(g)$
, then we set  $$ \begin{align*}\mathcal H^g = \{ h^g \mid h \in \mathcal H\}.\\[-15pt] \end{align*} $$
$$ \begin{align*}\mathcal H^g = \{ h^g \mid h \in \mathcal H\}.\\[-15pt] \end{align*} $$
-
• If
 $P\subseteq \mathcal L$
, then
$P\subseteq \mathcal L$
, then
 $N_{\mathcal L}(P)$
is the set of all
$N_{\mathcal L}(P)$
is the set of all
 $g\in \mathcal L$
such that
$g\in \mathcal L$
such that
 $P\subseteq \mathbf {D}(g)$
and
$P\subseteq \mathbf {D}(g)$
and
 $P^g=P$
. Similarly, if P and Q are subsets of
$P^g=P$
. Similarly, if P and Q are subsets of
 $\mathcal L$
, we write
$\mathcal L$
, we write
 $N_{\mathcal L}(P,Q)$
for the set of all
$N_{\mathcal L}(P,Q)$
for the set of all
 $g\in \mathcal L$
such that
$g\in \mathcal L$
such that
 $P\subseteq \mathbf {D}(g)$
and
$P\subseteq \mathbf {D}(g)$
and
 $P^g\subseteq Q$
.
$P^g\subseteq Q$
. -
• A partial subgroup is a subset
 $\mathcal H\subseteq \mathcal L$
such that
$\mathcal H\subseteq \mathcal L$
such that
 $h^{-1}\in \mathcal H$
for all
$h^{-1}\in \mathcal H$
for all
 $h\in \mathcal H$
and
$h\in \mathcal H$
and
 $\Pi (w)\in \mathcal H$
for all
$\Pi (w)\in \mathcal H$
for all
 $w\in \mathbf {D}(\mathcal L)\cap \mathbf {W}(\mathcal H)$
. A partial subgroup
$w\in \mathbf {D}(\mathcal L)\cap \mathbf {W}(\mathcal H)$
. A partial subgroup
 $\mathcal H$
of
$\mathcal H$
of
 $\mathcal L$
is a called a subgroup of
$\mathcal L$
is a called a subgroup of
 $\mathcal L$
if
$\mathcal L$
if
 $\mathbf {W}(\mathcal H)\subseteq \mathbf {D}(\mathcal L)$
.
$\mathbf {W}(\mathcal H)\subseteq \mathbf {D}(\mathcal L)$
. -
• If
 $\mathcal {N}$
is a partial subgroup of
$\mathcal {N}$
is a partial subgroup of
 $\mathcal L$
, then
$\mathcal L$
, then
 $\mathcal {N}$
is called a partial normal subgroup if
$\mathcal {N}$
is called a partial normal subgroup if
 $n^f\in \mathcal {N}$
for all
$n^f\in \mathcal {N}$
for all
 $f\in \mathcal L$
and all
$f\in \mathcal L$
and all
 $n\in \mathcal {N}\cap \mathbf {D}(f)$
.
$n\in \mathcal {N}\cap \mathbf {D}(f)$
.
We remark that a subgroup
![]() $\mathcal H$
of
$\mathcal H$
of
![]() $\mathcal L$
is always a group in the usual sense with the group multiplication defined by
$\mathcal L$
is always a group in the usual sense with the group multiplication defined by
![]() $hg=\Pi (h,g)$
for all
$hg=\Pi (h,g)$
for all
![]() $h,g\in \mathcal H$
. In particular, we can talk about p-subgroups of partial groups, meaning subgroups whose number of elements is a power of p.
$h,g\in \mathcal H$
. In particular, we can talk about p-subgroups of partial groups, meaning subgroups whose number of elements is a power of p.
2.2. Localities
Roughly speaking, localities are partial groups with some some extra structure, in particular, with a ‘Sylow p-subgroup’ and a set
![]() $\Delta $
of ‘objects’ that in a sense determines the domain of the product. Crucial is the following definition.
$\Delta $
of ‘objects’ that in a sense determines the domain of the product. Crucial is the following definition.
Definition 2.4. Let
![]() $\mathcal L$
be a partial group.
$\mathcal L$
be a partial group.
-
• If
 $\Delta $
is a collection of subgroups of
$\Delta $
is a collection of subgroups of
 $\mathcal L$
, define
$\mathcal L$
, define
 $\mathbf {D}_\Delta $
to be the set of words
$\mathbf {D}_\Delta $
to be the set of words
 $w=(g_1, \dots , g_k) \in \mathbf {W}(\mathcal L)$
such that there exist
$w=(g_1, \dots , g_k) \in \mathbf {W}(\mathcal L)$
such that there exist
 $P_0, \dots ,P_k \in \Delta $
with If such
$P_0, \dots ,P_k \in \Delta $
with If such $$ \begin{align*}P_{i-1} \subseteq \mathbf{D}(g_i)\mbox{ and }P_{i-1}^{g_i} = P_i\mbox{ for all }1 \leq i \leq k.\end{align*} $$
$$ \begin{align*}P_{i-1} \subseteq \mathbf{D}(g_i)\mbox{ and }P_{i-1}^{g_i} = P_i\mbox{ for all }1 \leq i \leq k.\end{align*} $$
 $P_0,\dots ,P_k$
are given, then we say also that
$P_0,\dots ,P_k$
are given, then we say also that
 $w\in \mathbf {D}_\Delta $
via
$w\in \mathbf {D}_\Delta $
via
 $P_0,P_1,\dots ,P_k$
or just that
$P_0,P_1,\dots ,P_k$
or just that
 $w\in \mathbf {D}_\Delta $
via
$w\in \mathbf {D}_\Delta $
via
 $P_0$
. In situations where we wish to stress the dependence of
$P_0$
. In situations where we wish to stress the dependence of
 $\mathbf {D}_\Delta $
on
$\mathbf {D}_\Delta $
on
 $\mathcal L$
and on the product
$\mathcal L$
and on the product
 $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
, we write
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
, we write
 $\mathbf {D}_\Delta (\mathcal L,\Pi )$
for
$\mathbf {D}_\Delta (\mathcal L,\Pi )$
for
 $\mathbf {D}_\Delta $
.
$\mathbf {D}_\Delta $
.
-
• Given a p-subgroup S of
 $\mathcal L$
and
$\mathcal L$
and
 $f\in \mathcal L$
, set If we want to stress the dependence of
$f\in \mathcal L$
, set If we want to stress the dependence of $$ \begin{align*}S_f:=\{x\in S\colon x\in\mathbf{D}(f)\mbox{ and }x^f\in S\}.\end{align*} $$
$$ \begin{align*}S_f:=\{x\in S\colon x\in\mathbf{D}(f)\mbox{ and }x^f\in S\}.\end{align*} $$
 $S_f$
on
$S_f$
on
 $\mathcal L$
and on the partial product and inversion on
$\mathcal L$
and on the partial product and inversion on
 $\mathcal L$
, then we write
$\mathcal L$
, then we write
 $S_f^{\mathcal L}$
for
$S_f^{\mathcal L}$
for
 $S_f$
.
$S_f$
.
Definition 2.5. Let
![]() $\mathcal L$
be a finite partial group, let S be a p-subgroup of
$\mathcal L$
be a finite partial group, let S be a p-subgroup of
![]() $\mathcal L$
and let
$\mathcal L$
and let
![]() $\Delta $
be a nonempty set of subgroups of S. We say that
$\Delta $
be a nonempty set of subgroups of S. We say that
![]() $(\mathcal L, \Delta , S)$
is a locality if the following hold:
$(\mathcal L, \Delta , S)$
is a locality if the following hold:
-
1. S is maximal with respect to inclusion among the p-subgroups of
 $\mathcal L$
.
$\mathcal L$
. -
2.
 $\mathbf {D} = \mathbf {D}_\Delta $
.
$\mathbf {D} = \mathbf {D}_\Delta $
. -
3.
 $\Delta $
is closed under taking
$\Delta $
is closed under taking
 $\mathcal L$
-conjugates and overgroups in S; that is, if
$\mathcal L$
-conjugates and overgroups in S; that is, if
 $P \in \Delta $
, then
$P \in \Delta $
, then
 $P^g\in \Delta $
for every
$P^g\in \Delta $
for every
 $g\in \mathcal L$
with
$g\in \mathcal L$
with
 $P \subseteq S_g$
, and every subgroup of S containing an element of
$P \subseteq S_g$
, and every subgroup of S containing an element of
 $\Delta $
is an element of
$\Delta $
is an element of
 $\Delta $
.
$\Delta $
.
We remark that the above definition of a locality is a reformulation of the one given by Chermak [Reference Chermak7, Definition 2.8]. As argued in [Reference Henke14, Remark 5.2], the two definitions are equivalent.
Example 2.6. Let M be a finite group,
![]() $S\in \mathrm {Syl}_p(M)$
and
$S\in \mathrm {Syl}_p(M)$
and
![]() $\mathcal {F}=\mathcal {F}_S(M)$
. Let
$\mathcal {F}=\mathcal {F}_S(M)$
. Let
![]() $\Gamma $
be a nonempty
$\Gamma $
be a nonempty
![]() $\mathcal {F}$
-closed collection of subgroups of S. Set
$\mathcal {F}$
-closed collection of subgroups of S. Set
and let
![]() $\mathbf {D}$
be the set of tuples
$\mathbf {D}$
be the set of tuples
![]() $(g_1,\dots ,g_n)\in \mathbf {W}(M)$
such that there exist
$(g_1,\dots ,g_n)\in \mathbf {W}(M)$
such that there exist
![]() $P_0,P_1,\dots ,P_n\in \Gamma $
with
$P_0,P_1,\dots ,P_n\in \Gamma $
with
 $P_{i-1}^{g_i}=P_i$
. Then
$P_{i-1}^{g_i}=P_i$
. Then
![]() $\mathcal L_\Gamma (M)$
forms a partial group whose product is the restriction of the multivariable product in M to
$\mathcal L_\Gamma (M)$
forms a partial group whose product is the restriction of the multivariable product in M to
![]() $\mathbf {D}$
and whose inversion map is the restriction of the inversion map on the group M to
$\mathbf {D}$
and whose inversion map is the restriction of the inversion map on the group M to
![]() $\mathcal L_\Gamma (M)$
. Moreover,
$\mathcal L_\Gamma (M)$
. Moreover,
![]() $(\mathcal L_\Gamma (M),\Gamma ,S)$
forms a locality. See [Reference Chermak6, Example/Lemma 2.10] for a proof.
$(\mathcal L_\Gamma (M),\Gamma ,S)$
forms a locality. See [Reference Chermak6, Example/Lemma 2.10] for a proof.
Lemma 2.7 Important properties of localities
If
![]() $(\mathcal L,\Delta ,S)$
is a locality, then the following hold:
$(\mathcal L,\Delta ,S)$
is a locality, then the following hold:
-
(a)
 $N_{\mathcal L}(P)$
is a subgroup of
$N_{\mathcal L}(P)$
is a subgroup of
 $\mathcal L$
for every
$\mathcal L$
for every
 $P\in \Delta $
.
$P\in \Delta $
. -
(b) Let
 $P\in \Delta $
and
$P\in \Delta $
and
 $g\in \mathcal L$
with
$g\in \mathcal L$
with
 $P\subseteq S_g$
. Then
$P\subseteq S_g$
. Then
 $Q:=P^g\in \Delta $
,
$Q:=P^g\in \Delta $
,
 $N_{\mathcal L}(P)\subseteq \mathbf {D}(g)$
and is an isomorphism of groups.
$N_{\mathcal L}(P)\subseteq \mathbf {D}(g)$
and is an isomorphism of groups. $$ \begin{align*}c_g\colon N_{\mathcal L}(P)\longrightarrow N_{\mathcal L}(Q)\end{align*} $$
$$ \begin{align*}c_g\colon N_{\mathcal L}(P)\longrightarrow N_{\mathcal L}(Q)\end{align*} $$
-
(c) Let
 $w=(g_1,\dots ,g_n)\in \mathbf {D}$
via
$w=(g_1,\dots ,g_n)\in \mathbf {D}$
via
 $(X_0,\dots ,X_n)$
. Then is a group isomorphism
$(X_0,\dots ,X_n)$
. Then is a group isomorphism $$ \begin{align*}c_{g_1}\circ \dots \circ c_{g_n}=c_{\Pi(w)}\end{align*} $$
$$ \begin{align*}c_{g_1}\circ \dots \circ c_{g_n}=c_{\Pi(w)}\end{align*} $$
 $N_{\mathcal L}(X_0)\longrightarrow N_{\mathcal L}(X_n)$
.
$N_{\mathcal L}(X_0)\longrightarrow N_{\mathcal L}(X_n)$
.
-
(d) For every
 $g\in \mathcal L$
,
$g\in \mathcal L$
,
 $S_g\in \Delta $
. In particular,
$S_g\in \Delta $
. In particular,
 $S_g$
is a subgroup of S. Moreover,
$S_g$
is a subgroup of S. Moreover,
 $S_g^g=S_{g^{-1}}$
and
$S_g^g=S_{g^{-1}}$
and
 $c_g\colon S_g\longrightarrow S$
is an injective group homomorphism.
$c_g\colon S_g\longrightarrow S$
is an injective group homomorphism. -
(e) For every
 $g\in \mathcal L$
,
$g\in \mathcal L$
,
 $c_g\colon \mathbf {D}(g)\longrightarrow \mathbf {D}(g^{-1})$
is a bijection with inverse map
$c_g\colon \mathbf {D}(g)\longrightarrow \mathbf {D}(g^{-1})$
is a bijection with inverse map
 $c_{g^{-1}}$
.
$c_{g^{-1}}$
. -
(f) For every
 $w\in \mathbf {W}(\mathcal L)$
,
$w\in \mathbf {W}(\mathcal L)$
,
 $S_w$
is a subgroup of
$S_w$
is a subgroup of
 $S_{\Pi (w)}$
, and
$S_{\Pi (w)}$
, and
 $S_w\in \Delta $
if and only if
$S_w\in \Delta $
if and only if
 $w\in \mathbf {D}$
.
$w\in \mathbf {D}$
.
Proof. Properties (a), (b) and (c) correspond to the statements in [Reference Chermak7, Lemma 2.3] except for the fact stated in (b) that
![]() $Q\in \Delta $
, which is, however, clearly true if one uses our definition of a locality. Property (d) holds by [Reference Chermak7, Proposition 2.6(a),(b)] and property (e) is stated in [Reference Chermak6, Lemma 2.5(c)]. Property (f) is [Reference Chermak7, Corollary 2.7].
$Q\in \Delta $
, which is, however, clearly true if one uses our definition of a locality. Property (d) holds by [Reference Chermak7, Proposition 2.6(a),(b)] and property (e) is stated in [Reference Chermak6, Lemma 2.5(c)]. Property (f) is [Reference Chermak7, Corollary 2.7].
Lemma 2.8. If
![]() $(\mathcal L,\Delta ,S)$
is a locality,
$(\mathcal L,\Delta ,S)$
is a locality,
![]() $r\in N_{\mathcal L}(S)$
and
$r\in N_{\mathcal L}(S)$
and
![]() $f\in \mathcal L$
, then
$f\in \mathcal L$
, then
![]() $(r,f)$
,
$(r,f)$
,
![]() $(f,r)$
and
$(f,r)$
and
![]() $(r^{-1},f,r)$
are words in
$(r^{-1},f,r)$
are words in
![]() $\mathbf {D}$
. Moreover,
$\mathbf {D}$
. Moreover,
 $$ \begin{align*}S_{(f,r)}=S_{fr}=S_f,\;S_{(r,f)}=S_{rf}=S_f^{r^{-1}}\mbox{ and }S_{f^r}=S_f^r.\end{align*} $$
$$ \begin{align*}S_{(f,r)}=S_{fr}=S_f,\;S_{(r,f)}=S_{rf}=S_f^{r^{-1}}\mbox{ and }S_{f^r}=S_f^r.\end{align*} $$
Proof. We will use Lemma 2.7(f) frequently in this proof without further reference. Because
 $S_f^r\leq S$
, we have
$S_f^r\leq S$
, we have
![]() $S_f\subseteq S_{(f,r)}$
. In particular, because
$S_f\subseteq S_{(f,r)}$
. In particular, because
![]() $S_f\in \Delta $
, we have
$S_f\in \Delta $
, we have
![]() $S_{(f,r)}\in \Delta $
and
$S_{(f,r)}\in \Delta $
and
![]() $(f,r)\in \mathbf {D}$
. So by [Reference Chermak7, Lemma 1.4(d)],
$(f,r)\in \mathbf {D}$
. So by [Reference Chermak7, Lemma 1.4(d)],
![]() $(f,r,r^{-1})\in \mathbf {D}$
and
$(f,r,r^{-1})\in \mathbf {D}$
and
![]() $f=\Pi (f,r,r^{-1})=(fr)r^{-1}$
. Applying the first stated property with
$f=\Pi (f,r,r^{-1})=(fr)r^{-1}$
. Applying the first stated property with
![]() $(fr,r^{-1})$
in place of
$(fr,r^{-1})$
in place of
![]() $(f,r)$
, we also get
$(f,r)$
, we also get
![]() $S_{fr}\subseteq S_{(fr,r^{-1})}$
. We see now that
$S_{fr}\subseteq S_{(fr,r^{-1})}$
. We see now that
Hence, all of the inclusions above are equalities and
![]() $S_f=S_{(f,r)}=S_{fr}$
.
$S_f=S_{(f,r)}=S_{fr}$
.
Similarly, because conjugation by r takes
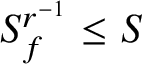 $S_f^{r^{-1}}\leq S$
to
$S_f^{r^{-1}}\leq S$
to
![]() $S_f$
, we have
$S_f$
, we have
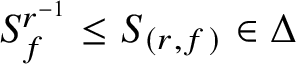 $S_f^{r^{-1}}\leq S_{(r,f)}\in \Delta $
and
$S_f^{r^{-1}}\leq S_{(r,f)}\in \Delta $
and
![]() $(r,f)\in \mathbf {D}$
. So by [Reference Chermak7, Lemma 1.4(d)],
$(r,f)\in \mathbf {D}$
. So by [Reference Chermak7, Lemma 1.4(d)],
![]() $(r^{-1},r,f)\in \mathbf {D}$
and
$(r^{-1},r,f)\in \mathbf {D}$
and
![]() $f=r^{-1}(rf)$
. Similarly,
$f=r^{-1}(rf)$
. Similarly,
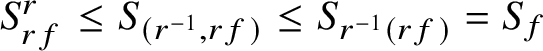 $S_{rf}^r\leq S_{(r^{-1},rf)}\leq S_{r^{-1}(rf)}=S_f$
and thus
$S_{rf}^r\leq S_{(r^{-1},rf)}\leq S_{r^{-1}(rf)}=S_f$
and thus
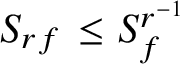 $S_{rf}\leq S_f^{r^{-1}}$
. Hence,
$S_{rf}\leq S_f^{r^{-1}}$
. Hence,
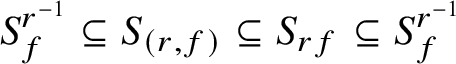 $$ \begin{align*}S_f^{r^{-1}}\subseteq S_{(r,f)}\subseteq S_{rf}\subseteq S_f^{r^{-1}}\end{align*} $$
$$ \begin{align*}S_f^{r^{-1}}\subseteq S_{(r,f)}\subseteq S_{rf}\subseteq S_f^{r^{-1}}\end{align*} $$
and equality holds everywhere above; that is,
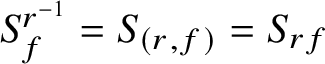 $S_f^{r^{-1}}=S_{(r,f)}=S_{rf}$
.
$S_f^{r^{-1}}=S_{(r,f)}=S_{rf}$
.
Note that
![]() $(r^{-1},f,r)\in \mathbf {D}$
via
$(r^{-1},f,r)\in \mathbf {D}$
via
![]() $S_f^r$
. Using the properties proved above, we see now that
$S_f^r$
. Using the properties proved above, we see now that
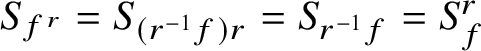 $S_{f^r}=S_{(r^{-1}f)r}=S_{r^{-1}f}=S_f^r$
.
$S_{f^r}=S_{(r^{-1}f)r}=S_{r^{-1}f}=S_f^r$
.
2.3. Fusion systems of localities
Similarly, because we can attach to a finite group a fusion system over a Sylow p-subgroup, we can attach a fusion system to a locality.
Definition 2.9. Let
![]() $(\mathcal L,\Delta ,S)$
be a locality.
$(\mathcal L,\Delta ,S)$
be a locality.
-
• For all
 $P,Q\in \Delta $
set
$P,Q\in \Delta $
set  $$ \begin{align*}\mathrm{Hom}_{\mathcal L}(P,Q):=\{c_g|_P\colon g\in N_{\mathcal L}(P,Q)\}.\end{align*} $$
$$ \begin{align*}\mathrm{Hom}_{\mathcal L}(P,Q):=\{c_g|_P\colon g\in N_{\mathcal L}(P,Q)\}.\end{align*} $$
-
• We write
 $\mathcal {F}_S(\mathcal L)$
for the smallest fusion system over S containing all of the conjugation maps
$\mathcal {F}_S(\mathcal L)$
for the smallest fusion system over S containing all of the conjugation maps
 $c_f\colon S_f\longrightarrow S$
with
$c_f\colon S_f\longrightarrow S$
with
 $f\in \mathcal L$
or, equivalently, for the fusion system generated by the sets
$f\in \mathcal L$
or, equivalently, for the fusion system generated by the sets
 $\mathrm {Hom}_{\mathcal L}(P,Q)$
, where
$\mathrm {Hom}_{\mathcal L}(P,Q)$
, where
 $P,Q$
are elements of
$P,Q$
are elements of
 $\Delta $
.
$\Delta $
. -
• We say that
 $(\mathcal L,\Delta ,S)$
is a locality over
$(\mathcal L,\Delta ,S)$
is a locality over
 $\mathcal {F}$
to indicate that
$\mathcal {F}$
to indicate that
 $\mathcal {F}=\mathcal {F}_S(\mathcal L)$
.
$\mathcal {F}=\mathcal {F}_S(\mathcal L)$
.
Lemma 2.10. If
![]() $(\mathcal L,\Delta ,S)$
is a locality over
$(\mathcal L,\Delta ,S)$
is a locality over
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $P\in \Delta $
, then the following hold:
$P\in \Delta $
, then the following hold:
-
(a) For every morphism
 $\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,S)$
, there exists
$\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,S)$
, there exists
 $f\in \mathcal L$
such that
$f\in \mathcal L$
such that
 $P\leq S_f$
and
$P\leq S_f$
and
 $\varphi =c_f|_P$
.
$\varphi =c_f|_P$
. -
(b) The subgroup P is fully
 $\mathcal {F}$
-normalised if and only if
$\mathcal {F}$
-normalised if and only if
 $N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
. Moreover, if so, then for every
$N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
. Moreover, if so, then for every
 $Q\in P^{\mathcal {F}}$
there exists
$Q\in P^{\mathcal {F}}$
there exists
 $g\in N_{\mathcal L}(N_S(Q),S)$
such that
$g\in N_{\mathcal L}(N_S(Q),S)$
such that
 $Q^g=P$
.
$Q^g=P$
. -
(c)
 $N_{\mathcal {F}}(P)=\mathcal {F}_{N_S(P)}(N_{\mathcal L}(P))$
.
$N_{\mathcal {F}}(P)=\mathcal {F}_{N_S(P)}(N_{\mathcal L}(P))$
.
Proof. For (a) see [Reference Henke14, Lemma 5.6]. Part (c) follows easily from (a). For the proof of (b) assume first that P is fully normalised. Because
![]() $N_S(P)$
is a p-subgroup of
$N_S(P)$
is a p-subgroup of
![]() $N_{\mathcal L}(P)$
, we can pick a Sylow p-subgroup T of
$N_{\mathcal L}(P)$
, we can pick a Sylow p-subgroup T of
![]() $N_{\mathcal L}(P)$
such that
$N_{\mathcal L}(P)$
such that
![]() $N_S(P)\leq T$
. By [Reference Chermak6, Proposition 2.22(b)], there exists
$N_S(P)\leq T$
. By [Reference Chermak6, Proposition 2.22(b)], there exists
![]() $x\in \mathcal L$
such that
$x\in \mathcal L$
such that
![]() $T\subseteq \mathbf {D}(x)$
and
$T\subseteq \mathbf {D}(x)$
and
![]() $T^x\leq S$
. Then, in particular,
$T^x\leq S$
. Then, in particular,
![]() $P\leq N_S(P)\leq S_x$
and by Lemma 2.7(b),
$P\leq N_S(P)\leq S_x$
and by Lemma 2.7(b),
![]() $T^x\leq N_S(P^x)$
. By (a), we have
$T^x\leq N_S(P^x)$
. By (a), we have
![]() $P^x\in P^{\mathcal {F}}$
and thus, because P is fully normalised,
$P^x\in P^{\mathcal {F}}$
and thus, because P is fully normalised,
![]() $|N_S(P^x)|\leq |N_S(P)|$
. On the other hand,
$|N_S(P^x)|\leq |N_S(P)|$
. On the other hand,
![]() $|N_S(P)|\leq |T|=|T^x|\leq |N_S(P^x)|$
. Hence, equality holds and thus
$|N_S(P)|\leq |T|=|T^x|\leq |N_S(P^x)|$
. Hence, equality holds and thus
![]() $N_S(P)=T$
is a Sylow p-subgroup of
$N_S(P)=T$
is a Sylow p-subgroup of
![]() $N_{\mathcal L}(P)$
.
$N_{\mathcal L}(P)$
.
Suppose now, on the other hand, that
![]() $N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
. Take
$N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
. Take
![]() $Q\in P^{\mathcal {F}}$
. By (a) there exists
$Q\in P^{\mathcal {F}}$
. By (a) there exists
![]() $f\in \mathcal L$
such that
$f\in \mathcal L$
such that
![]() $Q^f=P$
, and by Lemma 2.7(b) the map
$Q^f=P$
, and by Lemma 2.7(b) the map
![]() $c_f\colon N_{\mathcal L}(Q)\longrightarrow N_{\mathcal L}(P)$
is an isomorphism of groups. Hence,
$c_f\colon N_{\mathcal L}(Q)\longrightarrow N_{\mathcal L}(P)$
is an isomorphism of groups. Hence,
![]() $N_S(Q)^f$
is a p-subgroup of
$N_S(Q)^f$
is a p-subgroup of
![]() $N_{\mathcal L}(P)$
. Because
$N_{\mathcal L}(P)$
. Because
![]() $N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
, by Sylow’s theorem there exists
$N_S(P)\in \mathrm {Syl}_p(N_{\mathcal L}(P))$
, by Sylow’s theorem there exists
![]() $a\in N_{\mathcal L}(P)$
such that
$a\in N_{\mathcal L}(P)$
such that
![]() $N_S(Q)^{fa}=(N_S(Q)^f)^a\leq N_S(P)$
, where the equality uses Lemma 2.7(c). Then
$N_S(Q)^{fa}=(N_S(Q)^f)^a\leq N_S(P)$
, where the equality uses Lemma 2.7(c). Then
![]() $g:=fa\in N_{\mathcal L}(N_S(Q),S)$
with
$g:=fa\in N_{\mathcal L}(N_S(Q),S)$
with
![]() $Q^g=(Q^f)^a=P^a=P$
. Moreover,
$Q^g=(Q^f)^a=P^a=P$
. Moreover,
![]() $|N_S(Q)|=|N_S(Q)^g|\leq |N_S(P)|$
. Because
$|N_S(Q)|=|N_S(Q)^g|\leq |N_S(P)|$
. Because
![]() $Q\in P^{\mathcal {F}}$
was arbitrary, this shows that P is fully normalised. Hence, (b) holds.
$Q\in P^{\mathcal {F}}$
was arbitrary, this shows that P is fully normalised. Hence, (b) holds.
If
![]() $(\mathcal L,\Delta ,S)$
is a locality and
$(\mathcal L,\Delta ,S)$
is a locality and
![]() $\mathcal {F}=\mathcal {F}_S(\mathcal L)$
, then notice that
$\mathcal {F}=\mathcal {F}_S(\mathcal L)$
, then notice that
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {F}$
-closed as defined next.
$\mathcal {F}$
-closed as defined next.
Definition 2.11. Let
![]() $\mathcal {F}$
be a fusion system over S, and let
$\mathcal {F}$
be a fusion system over S, and let
![]() $\Delta $
be a set of subgroups of S.
$\Delta $
be a set of subgroups of S.
-
• The set
 $\Delta $
is closed under
$\Delta $
is closed under
 $\mathcal {F}$
-conjugacy if
$\mathcal {F}$
-conjugacy if
 $P^{\mathcal {F}}\subseteq \Delta $
for every
$P^{\mathcal {F}}\subseteq \Delta $
for every
 $P\in \Delta $
.
$P\in \Delta $
. -
• We call
 $\Delta \mathcal {F}$
-closed if
$\Delta \mathcal {F}$
-closed if
 $\Delta $
is both closed under
$\Delta $
is both closed under
 $\mathcal {F}$
-conjugacy and overgroup closed in S.
$\mathcal {F}$
-conjugacy and overgroup closed in S.
Important examples of
![]() $\mathcal {F}$
-closed collections are the set
$\mathcal {F}$
-closed collections are the set
![]() $\mathcal {F}^c$
of
$\mathcal {F}^c$
of
![]() $\mathcal {F}$
-centric subgroups (cf. [Reference Aschbacher, Kessar and Oliver1, Definition 3.1]), the set
$\mathcal {F}$
-centric subgroups (cf. [Reference Aschbacher, Kessar and Oliver1, Definition 3.1]), the set
![]() $\mathcal {F}^q$
of
$\mathcal {F}^q$
of
![]() $\mathcal {F}$
-quasicentric subgroups (cf. Definition 4.5 and Lemma 4.6(d) in Reference Aschbacher, Kessar and Oliver[1]) and the set
$\mathcal {F}$
-quasicentric subgroups (cf. Definition 4.5 and Lemma 4.6(d) in Reference Aschbacher, Kessar and Oliver[1]) and the set
![]() $\mathcal {F}^s$
of subcentric subgroups (cf. Definition 1 and Proposition 3.3 in Reference Henke[14]).
$\mathcal {F}^s$
of subcentric subgroups (cf. Definition 1 and Proposition 3.3 in Reference Henke[14]).
2.4. Morphisms of fusion systems
Throughout this subsection let
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() ${\widetilde {\mathcal {F}}}$
be fusion systems over S and
${\widetilde {\mathcal {F}}}$
be fusion systems over S and
![]() ${\widetilde {S}}$
, respectively.
${\widetilde {S}}$
, respectively.
Definition 2.12. We say that a group homomorphism
![]() $\alpha \colon S\longrightarrow {\widetilde {S}}$
induces a morphism from
$\alpha \colon S\longrightarrow {\widetilde {S}}$
induces a morphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
if, for each
${\widetilde {\mathcal {F}}}$
if, for each
![]() $\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
, there exists
$\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
, there exists
![]() $\psi \in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
such that
$\psi \in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
such that
![]() $(\alpha |_P)\psi =\varphi (\alpha |_Q)$
.
$(\alpha |_P)\psi =\varphi (\alpha |_Q)$
.
Note that, for any
![]() $\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
, a map
$\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
, a map
![]() $\psi \in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
as in the above definition is uniquely determined. So if
$\psi \in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
as in the above definition is uniquely determined. So if
![]() $\alpha $
induces a morphism from
$\alpha $
induces a morphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
, then
${\widetilde {\mathcal {F}}}$
, then
![]() $\alpha $
induces a map
$\alpha $
induces a map
Together with the map
![]() $P\mapsto P\alpha $
from the set of objects of
$P\mapsto P\alpha $
from the set of objects of
![]() $\mathcal {F}$
to the set of objects of
$\mathcal {F}$
to the set of objects of
![]() ${\widetilde {\mathcal {F}}}$
this gives a functor from
${\widetilde {\mathcal {F}}}$
this gives a functor from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
. Moreover,
${\widetilde {\mathcal {F}}}$
. Moreover,
![]() $\alpha $
together with the maps
$\alpha $
together with the maps
![]() $\alpha _{P,Q}$
(
$\alpha _{P,Q}$
(
![]() $P,Q\leq S$
) is a morphism of fusion systems in the sense of [Reference Aschbacher, Kessar and Oliver1, Definition II.2.2]. We call
$P,Q\leq S$
) is a morphism of fusion systems in the sense of [Reference Aschbacher, Kessar and Oliver1, Definition II.2.2]. We call
![]() $(\alpha ,\alpha _{P,Q}\colon P,Q\leq S)$
the morphism induced by
$(\alpha ,\alpha _{P,Q}\colon P,Q\leq S)$
the morphism induced by
![]() $\alpha $
.
$\alpha $
.
Definition 2.13. Suppose that
![]() $\alpha \colon S\longrightarrow {\widetilde {S}}$
induces a morphism from
$\alpha \colon S\longrightarrow {\widetilde {S}}$
induces a morphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
. We say that
${\widetilde {\mathcal {F}}}$
. We say that
![]() $\alpha $
induces an epimorphism from
$\alpha $
induces an epimorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
if the induced morphism
${\widetilde {\mathcal {F}}}$
if the induced morphism
![]() $(\alpha ,\alpha _{P,Q}\colon P,Q\leq S)$
is a surjective morphism of fusion systems. This means that
$(\alpha ,\alpha _{P,Q}\colon P,Q\leq S)$
is a surjective morphism of fusion systems. This means that
![]() $\alpha $
is surjective as a map
$\alpha $
is surjective as a map
![]() $S\longrightarrow {\widetilde {S}}$
and
$S\longrightarrow {\widetilde {S}}$
and
![]() $\mathcal {F}\alpha ^*={\widetilde {\mathcal {F}}}$
; that is, for all
$\mathcal {F}\alpha ^*={\widetilde {\mathcal {F}}}$
; that is, for all
![]() $P,Q\leq S$
with
$P,Q\leq S$
with
![]() $\ker (\alpha )\leq P\cap Q$
, the map
$\ker (\alpha )\leq P\cap Q$
, the map
![]() $\alpha _{P,Q}$
is surjective. If
$\alpha _{P,Q}$
is surjective. If
![]() $\alpha $
is in addition injective, then we say that
$\alpha $
is in addition injective, then we say that
![]() $\alpha $
induces an isomorphism from
$\alpha $
induces an isomorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
. If
${\widetilde {\mathcal {F}}}$
. If
![]() $\alpha \in \mathrm {Aut}(S)$
and
$\alpha \in \mathrm {Aut}(S)$
and
![]() $\alpha $
induces a morphism from
$\alpha $
induces a morphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {F}$
, then we say that
$\mathcal {F}$
, then we say that
![]() $\alpha $
induces an automorphism of
$\alpha $
induces an automorphism of
![]() $\mathcal {F}$
. We will write
$\mathcal {F}$
. We will write
![]() $\mathrm {Aut}(\mathcal {F})$
for the set of automorphisms of S that induce an automorphism of
$\mathrm {Aut}(\mathcal {F})$
for the set of automorphisms of S that induce an automorphism of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
If
![]() $\alpha \colon S\longrightarrow {\widetilde {S}}$
is an isomorphism of groups, then it is easy to see that
$\alpha \colon S\longrightarrow {\widetilde {S}}$
is an isomorphism of groups, then it is easy to see that
![]() $\alpha $
induces an isomorphism from
$\alpha $
induces an isomorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
if and only if, for all
${\widetilde {\mathcal {F}}}$
if and only if, for all
![]() $P,Q\leq S$
and every group homomorphism
$P,Q\leq S$
and every group homomorphism
![]() $\varphi \colon P\longrightarrow Q$
,
$\varphi \colon P\longrightarrow Q$
,
 $$ \begin{align*}\varphi\in\mathrm{Hom}_{\mathcal{F}}(P,Q)\Longleftrightarrow \alpha^{-1}\varphi\alpha\in\mathrm{Hom}_{{\widetilde{\mathcal{F}}}}(P\alpha,Q\alpha);\end{align*} $$
$$ \begin{align*}\varphi\in\mathrm{Hom}_{\mathcal{F}}(P,Q)\Longleftrightarrow \alpha^{-1}\varphi\alpha\in\mathrm{Hom}_{{\widetilde{\mathcal{F}}}}(P\alpha,Q\alpha);\end{align*} $$
if so, then the map
![]() $\alpha _{P,Q}$
as above is given by
$\alpha _{P,Q}$
as above is given by
![]() $\varphi \mapsto \alpha ^{-1}\varphi \alpha $
. It follows from this observation that
$\varphi \mapsto \alpha ^{-1}\varphi \alpha $
. It follows from this observation that
![]() $\alpha $
induces an isomorphism from
$\alpha $
induces an isomorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
if and only if the inverse map
${\widetilde {\mathcal {F}}}$
if and only if the inverse map
![]() $\alpha ^{-1}$
induces an isomorphism from
$\alpha ^{-1}$
induces an isomorphism from
![]() ${\widetilde {\mathcal {F}}}$
to
${\widetilde {\mathcal {F}}}$
to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Lemma 2.14. Suppose that
![]() $\alpha \colon S\longrightarrow {\widetilde {S}}$
induces an epimorphism from
$\alpha \colon S\longrightarrow {\widetilde {S}}$
induces an epimorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() ${\widetilde {\mathcal {F}}}$
. Let
${\widetilde {\mathcal {F}}}$
. Let
![]() $\ker (\alpha )\leq R\leq S$
. Then the following hold:
$\ker (\alpha )\leq R\leq S$
. Then the following hold:
-
(a)
 $(R\alpha )^{{\widetilde {\mathcal {F}}}}=\{R_0\alpha \colon R_0\in R^{\mathcal {F}}\}$
.
$(R\alpha )^{{\widetilde {\mathcal {F}}}}=\{R_0\alpha \colon R_0\in R^{\mathcal {F}}\}$
. -
(b) The subgroup R is fully normalised if and only if
 $R\alpha $
is fully normalised.
$R\alpha $
is fully normalised. -
(c) The group homomorphism
 $\alpha |_{N_S(R)}\colon N_S(R)\longrightarrow N_{{\widetilde {S}}}(R\alpha )$
induces an epimorphism from
$\alpha |_{N_S(R)}\colon N_S(R)\longrightarrow N_{{\widetilde {S}}}(R\alpha )$
induces an epimorphism from
 $N_{\mathcal {F}}(R)$
to
$N_{\mathcal {F}}(R)$
to
 $N_{{\widetilde {\mathcal {F}}}}(R\alpha )$
.
$N_{{\widetilde {\mathcal {F}}}}(R\alpha )$
.
Proof. Property (a) is elementary to check, and property (b) follows from (a) because
![]() $N_S(R_0)\alpha =N_{{\widetilde {S}}}(R_0\alpha )$
has order
$N_S(R_0)\alpha =N_{{\widetilde {S}}}(R_0\alpha )$
has order
![]() $|N_S(R_0)|/|\ker (\alpha )|$
for all
$|N_S(R_0)|/|\ker (\alpha )|$
for all
![]() $R_0\in R^{\mathcal {F}}$
.
$R_0\in R^{\mathcal {F}}$
.
For the proof of (c) let
![]() $P,Q\leq N_S(R)$
with
$P,Q\leq N_S(R)$
with
![]() $\ker (\alpha )\leq P\cap Q$
,
$\ker (\alpha )\leq P\cap Q$
,
![]() $\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
and
$\varphi \in \mathrm {Hom}_{\mathcal {F}}(P,Q)$
and
![]() $\psi =\varphi \alpha _{P,Q}\in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
. We then have
$\psi =\varphi \alpha _{P,Q}\in \mathrm {Hom}_{{\widetilde {\mathcal {F}}}}(P\alpha ,Q\alpha )$
. We then have
![]() $\alpha |_P\psi =\varphi \alpha |_Q$
. Moreover, if
$\alpha |_P\psi =\varphi \alpha |_Q$
. Moreover, if
![]() $R\leq P$
, then
$R\leq P$
, then
![]() $\ker (\alpha )\leq R\varphi $
as
$\ker (\alpha )\leq R\varphi $
as
![]() $\ker (\alpha )$
is strongly closed. Hence,
$\ker (\alpha )$
is strongly closed. Hence,
![]() $R\leq P\cap Q$
and
$R\leq P\cap Q$
and
![]() $R\varphi =R$
if and only if
$R\varphi =R$
if and only if
![]() $R\alpha \leq P\alpha \cap Q\alpha $
and
$R\alpha \leq P\alpha \cap Q\alpha $
and
![]() $(R\alpha )\psi =(R\varphi )\alpha =R\alpha $
. This implies (c).
$(R\alpha )\psi =(R\varphi )\alpha =R\alpha $
. This implies (c).
Lemma 2.15. Let
![]() $\alpha \colon G\longrightarrow \tilde {G}$
be an epimorphism from a group G to a group
$\alpha \colon G\longrightarrow \tilde {G}$
be an epimorphism from a group G to a group
![]() $\tilde {G}$
. Let
$\tilde {G}$
. Let
![]() $S\in \mathrm {Syl}_p(G)$
and
$S\in \mathrm {Syl}_p(G)$
and
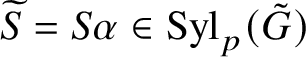 ${\widetilde {S}}=S\alpha \in \mathrm {Syl}_p(\tilde {G})$
. Then
${\widetilde {S}}=S\alpha \in \mathrm {Syl}_p(\tilde {G})$
. Then
![]() $\alpha |_S$
induces an epimorphism from
$\alpha |_S$
induces an epimorphism from
![]() $\mathcal {F}_S(G)$
to
$\mathcal {F}_S(G)$
to
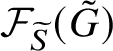 $\mathcal {F}_{{\widetilde {S}}}(\tilde {G})$
.
$\mathcal {F}_{{\widetilde {S}}}(\tilde {G})$
.
Proof. Let
![]() $P,Q$
be subgroups of S. If
$P,Q$
be subgroups of S. If
![]() $g\in G$
with
$g\in G$
with
![]() $P^g\leq Q\leq S$
, then
$P^g\leq Q\leq S$
, then
![]() $(P\alpha )^{g\alpha }=P^g\alpha \leq Q\alpha \leq {\widetilde {S}}$
and
$(P\alpha )^{g\alpha }=P^g\alpha \leq Q\alpha \leq {\widetilde {S}}$
and
![]() $(\alpha |_P) (c_{g\alpha }|_{P\alpha })=(c_g|_P)(\alpha |_Q)$
. So
$(\alpha |_P) (c_{g\alpha }|_{P\alpha })=(c_g|_P)(\alpha |_Q)$
. So
![]() $\alpha |_S$
is fusion preserving and the corresponding morphism of fusion systems takes
$\alpha |_S$
is fusion preserving and the corresponding morphism of fusion systems takes
![]() $c_g|_P$
to
$c_g|_P$
to
![]() $c_{g\alpha }|_{P\alpha }$
. To show that
$c_{g\alpha }|_{P\alpha }$
. To show that
![]() $\alpha |_S$
induces an epimorphism, assume now that
$\alpha |_S$
induces an epimorphism, assume now that
![]() $\ker (\alpha |_S)\leq P\cap Q$
and fix
$\ker (\alpha |_S)\leq P\cap Q$
and fix
![]() $h\in \tilde {G}$
with
$h\in \tilde {G}$
with
![]() $(P\alpha )^h\leq Q\alpha $
. Because
$(P\alpha )^h\leq Q\alpha $
. Because
![]() $\alpha $
is an epimorphism, there exists
$\alpha $
is an epimorphism, there exists
![]() $g\in G$
with
$g\in G$
with
![]() $g\alpha =h$
. We then have
$g\alpha =h$
. We then have
![]() $P^g\alpha =(P\alpha )^h\leq Q\alpha $
. Because
$P^g\alpha =(P\alpha )^h\leq Q\alpha $
. Because
![]() $\ker (\alpha |_S)=\ker (\alpha )\cap S\leq Q$
, the group Q is a Sylow p-subgroup of
$\ker (\alpha |_S)=\ker (\alpha )\cap S\leq Q$
, the group Q is a Sylow p-subgroup of
![]() $\ker (\alpha )Q$
, which is the preimage of
$\ker (\alpha )Q$
, which is the preimage of
![]() $Q\alpha $
in G. Thus, by Sylow’s theorem, there exists
$Q\alpha $
in G. Thus, by Sylow’s theorem, there exists
![]() $n\in \ker (\alpha )$
with
$n\in \ker (\alpha )$
with
![]() $P^{gn}\leq Q$
. Replacing g by
$P^{gn}\leq Q$
. Replacing g by
![]() $gn$
, we may assume that
$gn$
, we may assume that
![]() $P^g\leq Q$
. As seen at the beginning, this means that
$P^g\leq Q$
. As seen at the beginning, this means that
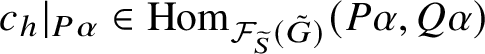 $c_h|_{P\alpha }\in \mathrm {Hom}_{\mathcal {F}_{{\widetilde {S}}}(\tilde {G})}(P\alpha ,Q\alpha )$
is the image of
$c_h|_{P\alpha }\in \mathrm {Hom}_{\mathcal {F}_{{\widetilde {S}}}(\tilde {G})}(P\alpha ,Q\alpha )$
is the image of
![]() $c_g|_P\in \mathrm {Hom}_{\mathcal {F}_S(G)}(P,Q)$
under the morphism induced by
$c_g|_P\in \mathrm {Hom}_{\mathcal {F}_S(G)}(P,Q)$
under the morphism induced by
![]() $\alpha $
.
$\alpha $
.
2.5. Homomorphisms of partial groups
In this subsection, we will introduce natural notions of homomorphisms, projections, isomorphisms and automorphisms of partial groups and of localities. Moreover, we state a few simple results needed in the proofs of our main theorems.
Notation 2.16. If
![]() $\mathcal L$
and
$\mathcal L$
and
![]() ${\widetilde {\mathcal {L}}}$
are sets and
${\widetilde {\mathcal {L}}}$
are sets and
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}},f\mapsto f\alpha $
is a map, then we denote by
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}},f\mapsto f\alpha $
is a map, then we denote by
![]() $\alpha ^*$
the induced map on words
$\alpha ^*$
the induced map on words
If
![]() $\mathbf {D}\subseteq \mathbf {W}(\mathcal L)$
, set
$\mathbf {D}\subseteq \mathbf {W}(\mathcal L)$
, set
![]() $\mathbf {D}\alpha ^*:=\{w\alpha ^*\colon w\in \mathbf {D}\}$
.
$\mathbf {D}\alpha ^*:=\{w\alpha ^*\colon w\in \mathbf {D}\}$
.
For the remainder of this subsection let
![]() $\mathcal L$
and
$\mathcal L$
and
![]() ${\widetilde {\mathcal {L}}}$
be partial groups with products
${\widetilde {\mathcal {L}}}$
be partial groups with products
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
![]() $\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\longrightarrow {\widetilde {\mathcal {L}}}$
, respectively.
$\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\longrightarrow {\widetilde {\mathcal {L}}}$
, respectively.
Definition 2.17. A map
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is called a homomorphism of partial groups if
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is called a homomorphism of partial groups if
-
1.
 $\mathbf {D}\alpha ^* \subseteq \widetilde {\mathbf {D}}$
; and
$\mathbf {D}\alpha ^* \subseteq \widetilde {\mathbf {D}}$
; and -
2.
 $\Pi (w)\alpha = \widetilde {\Pi }(w\alpha ^*)$
for every
$\Pi (w)\alpha = \widetilde {\Pi }(w\alpha ^*)$
for every
 $w \in \mathbf {D}$
.
$w \in \mathbf {D}$
.
If, moreover,
![]() $\mathbf {D}\alpha ^* = \widetilde {\mathbf {D}}$
, then we say that
$\mathbf {D}\alpha ^* = \widetilde {\mathbf {D}}$
, then we say that
![]() $\alpha $
is a projection of partial groups. If
$\alpha $
is a projection of partial groups. If
![]() $\alpha $
is injective and
$\alpha $
is injective and
![]() $\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
, then
$\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
, then
![]() $\alpha $
is called an isomorphism. The isomorphisms of partial groups from
$\alpha $
is called an isomorphism. The isomorphisms of partial groups from
![]() $\mathcal L$
to itself are called automorphisms and the set of these automorphisms is denoted by
$\mathcal L$
to itself are called automorphisms and the set of these automorphisms is denoted by
![]() $\mathrm {Aut}(\mathcal L)$
.
$\mathrm {Aut}(\mathcal L)$
.
For any homomorphism
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
, we call
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
, we call
![]() $\ker (\alpha )=\{f\in \mathcal L\colon f\alpha =\operatorname {\mathbf {1}}\}$
the kernel of
$\ker (\alpha )=\{f\in \mathcal L\colon f\alpha =\operatorname {\mathbf {1}}\}$
the kernel of
![]() $\alpha $
.
$\alpha $
.
Notice that every projection
![]() $\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is surjective, because
$\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is surjective, because
![]() $\widetilde {\mathbf {D}}$
contains all of the words of length one. In particular, every isomorphism is a bijection. In fact, there is the following characterization of isomorphisms.
$\widetilde {\mathbf {D}}$
contains all of the words of length one. In particular, every isomorphism is a bijection. In fact, there is the following characterization of isomorphisms.
Lemma 2.18. A map
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is an isomorphism of partial groups if and only if
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is an isomorphism of partial groups if and only if
![]() $\alpha $
is bijective and
$\alpha $
is bijective and
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{-1}$
are both homomorphisms of partial groups.
$\alpha ^{-1}$
are both homomorphisms of partial groups.
Proof. If
![]() $\alpha $
is bijective and
$\alpha $
is bijective and
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{-1}$
are both homomorphisms of partial groups, then
$\alpha ^{-1}$
are both homomorphisms of partial groups, then
![]() $\mathbf {D}\alpha ^*\subseteq \widetilde {\mathbf {D}}$
and
$\mathbf {D}\alpha ^*\subseteq \widetilde {\mathbf {D}}$
and
![]() $\widetilde {\mathbf {D}}(\alpha ^{-1})^*\subseteq \mathbf {D}$
, with the latter inclusion implying
$\widetilde {\mathbf {D}}(\alpha ^{-1})^*\subseteq \mathbf {D}$
, with the latter inclusion implying
![]() $\widetilde {\mathbf {D}}\subseteq \mathbf {D}\alpha ^*$
. Thus, we get
$\widetilde {\mathbf {D}}\subseteq \mathbf {D}\alpha ^*$
. Thus, we get
![]() $\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
. Because
$\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
. Because
![]() $\alpha $
is an injective homomorphism of partial groups, this yields that
$\alpha $
is an injective homomorphism of partial groups, this yields that
![]() $\alpha $
is an isomorphism of partial groups.
$\alpha $
is an isomorphism of partial groups.
Assume now that
![]() $\alpha $
is an isomorphism of partial groups. Then
$\alpha $
is an isomorphism of partial groups. Then
![]() $\alpha $
is a bijection. Moreover,
$\alpha $
is a bijection. Moreover,
![]() $\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
and thus
$\mathbf {D}\alpha ^*=\widetilde {\mathbf {D}}$
and thus
![]() $\widetilde {\mathbf {D}}(\alpha ^{-1})^*=\mathbf {D}$
. Given
$\widetilde {\mathbf {D}}(\alpha ^{-1})^*=\mathbf {D}$
. Given
![]() $w\in \widetilde {\mathbf {D}}$
, it remains to show that
$w\in \widetilde {\mathbf {D}}$
, it remains to show that
![]() $\widetilde {\Pi }(w)\alpha ^{-1}=\Pi (w(\alpha ^{-1})^*)$
. Note that
$\widetilde {\Pi }(w)\alpha ^{-1}=\Pi (w(\alpha ^{-1})^*)$
. Note that
![]() $w(\alpha ^{-1})^*\in \mathbf {D}$
and thus, because
$w(\alpha ^{-1})^*\in \mathbf {D}$
and thus, because
![]() $\alpha $
is a homomorphism of partial groups,
$\alpha $
is a homomorphism of partial groups,
![]() $\Pi (w(\alpha ^{-1})^*)\alpha =\widetilde {\Pi }(w(\alpha ^{-1})^*\alpha ^*)=\widetilde {\Pi }(w)$
. This implies the required equality.
$\Pi (w(\alpha ^{-1})^*)\alpha =\widetilde {\Pi }(w(\alpha ^{-1})^*\alpha ^*)=\widetilde {\Pi }(w)$
. This implies the required equality.
Lemma 2.19. Suppose that
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups. If M is a subgroup of
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups. If M is a subgroup of
![]() $\mathcal L$
, then
$\mathcal L$
, then
![]() $M\alpha $
is a subgroup of
$M\alpha $
is a subgroup of
![]() ${\widetilde {\mathcal {L}}}$
and
${\widetilde {\mathcal {L}}}$
and
![]() $\alpha $
restricts to a group homomorphism
$\alpha $
restricts to a group homomorphism
![]() $M\longrightarrow M\alpha $
.
$M\longrightarrow M\alpha $
.
Proof. If
![]() $w=(f_1,\dots ,f_n)\in \mathbf {W}(M\alpha )$
, then for
$w=(f_1,\dots ,f_n)\in \mathbf {W}(M\alpha )$
, then for
![]() $i=1,\dots ,n$
, there exists
$i=1,\dots ,n$
, there exists
![]() $g_i\in M$
such that
$g_i\in M$
such that
![]() $f_i=g_i\alpha $
. It follows that
$f_i=g_i\alpha $
. It follows that
![]() $u:=(g_1,\dots ,g_n)\in \mathbf {W}(M)\subseteq \mathbf {D}$
and
$u:=(g_1,\dots ,g_n)\in \mathbf {W}(M)\subseteq \mathbf {D}$
and
![]() $w=u\alpha ^*\in \widetilde {\mathbf {D}}$
. Moreover,
$w=u\alpha ^*\in \widetilde {\mathbf {D}}$
. Moreover,
![]() $\widetilde {\Pi }(w)=\widetilde {\Pi }(u\alpha ^*)=\Pi (u)\alpha \in M\alpha $
because M is a subgroup. Hence,
$\widetilde {\Pi }(w)=\widetilde {\Pi }(u\alpha ^*)=\Pi (u)\alpha \in M\alpha $
because M is a subgroup. Hence,
![]() $M\alpha $
is a subgroup of
$M\alpha $
is a subgroup of
![]() ${\widetilde {\mathcal {L}}}$
. The assertion follows because
${\widetilde {\mathcal {L}}}$
. The assertion follows because
![]() $(gh)\alpha =\Pi (v)\alpha =\widetilde {\Pi }(v\alpha ^*)=(g\alpha )(h\alpha )$
for every word
$(gh)\alpha =\Pi (v)\alpha =\widetilde {\Pi }(v\alpha ^*)=(g\alpha )(h\alpha )$
for every word
![]() $v=(g,h)\in \mathbf {W}(M)$
of length two.
$v=(g,h)\in \mathbf {W}(M)$
of length two.
We now turn attention to maps between localities.
Definition 2.20. Let
![]() $(\mathcal L, \Delta , S)$
and
$(\mathcal L, \Delta , S)$
and
![]() $({\widetilde {\mathcal {L}}}, \widetilde {\Delta },{\widetilde {S}})$
be localities and let
$({\widetilde {\mathcal {L}}}, \widetilde {\Delta },{\widetilde {S}})$
be localities and let
![]() $\alpha \colon \mathcal L \longrightarrow {\widetilde {\mathcal {L}}}$
be a projection of partial groups.
$\alpha \colon \mathcal L \longrightarrow {\widetilde {\mathcal {L}}}$
be a projection of partial groups.
-
• For any set
 $\Gamma $
of subgroups of
$\Gamma $
of subgroups of
 $\mathcal L$
, set
$\mathcal L$
, set  $$ \begin{align*}\Gamma\alpha:=\{P\alpha\colon P\in\Gamma\}.\end{align*} $$
$$ \begin{align*}\Gamma\alpha:=\{P\alpha\colon P\in\Gamma\}.\end{align*} $$
-
• We say that
 $\alpha $
is a projection of localities from
$\alpha $
is a projection of localities from
 $(\mathcal L,\Delta ,S)$
to
$(\mathcal L,\Delta ,S)$
to
 $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
if
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
if
 $\Delta \alpha = \widetilde {\Delta }$
.
$\Delta \alpha = \widetilde {\Delta }$
. -
• If
 $\alpha $
is a projection of localities that is injective (and thus an isomorphism of partial groups), then
$\alpha $
is a projection of localities that is injective (and thus an isomorphism of partial groups), then
 $\alpha $
is a called an isomorphism of localities. We write
$\alpha $
is a called an isomorphism of localities. We write
 $\mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))$
for the set of isomorphisms from
$\mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))$
for the set of isomorphisms from
 $(\mathcal L,\Delta ,S)$
to
$(\mathcal L,\Delta ,S)$
to
 $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
(which may be empty).
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
(which may be empty). -
• Given a set
 $\Gamma $
of subgroups of S and a set
$\Gamma $
of subgroups of S and a set
 $\widetilde {\Gamma }$
of subgroups of
$\widetilde {\Gamma }$
of subgroups of
 ${\widetilde {S}}$
, we write for the set of isomorphisms
${\widetilde {S}}$
, we write for the set of isomorphisms $$ \begin{align*}\mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Gamma,\widetilde{\Gamma}}\end{align*} $$
$$ \begin{align*}\mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Gamma,\widetilde{\Gamma}}\end{align*} $$
 $\alpha $
from
$\alpha $
from
 $(\mathcal L,\Delta ,S)$
to
$(\mathcal L,\Delta ,S)$
to
 $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
with
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
with
 $\Gamma \alpha =\widetilde {\Gamma }$
.
$\Gamma \alpha =\widetilde {\Gamma }$
.
-
• An isomorphism from
 $(\mathcal L,\Delta ,S)$
to itself is called an automorphism. We write
$(\mathcal L,\Delta ,S)$
to itself is called an automorphism. We write
 $\mathrm {Aut}(\mathcal L,\Delta ,S)$
for the group of automorphisms of
$\mathrm {Aut}(\mathcal L,\Delta ,S)$
for the group of automorphisms of
 $(\mathcal L,\Delta ,S)$
. If
$(\mathcal L,\Delta ,S)$
. If
 $\Gamma $
is a set of subgroups of S, then
$\Gamma $
is a set of subgroups of S, then
 $\mathrm {Aut}(\mathcal L,\Delta ,S)_{\Gamma }$
denotes the set of automorphisms
$\mathrm {Aut}(\mathcal L,\Delta ,S)_{\Gamma }$
denotes the set of automorphisms
 $\alpha $
of
$\alpha $
of
 $(\mathcal L,\Delta ,S)$
with
$(\mathcal L,\Delta ,S)$
with
 $\Gamma \alpha =\Gamma $
.
$\Gamma \alpha =\Gamma $
. -
• An automorphism of
 $(\mathcal L,\Delta ,S)$
is called rigid if it restricts to the identity on S.
$(\mathcal L,\Delta ,S)$
is called rigid if it restricts to the identity on S.
If
![]() $\alpha $
is a projection of localities from
$\alpha $
is a projection of localities from
![]() $(\mathcal L,\Delta ,S)$
to
$(\mathcal L,\Delta ,S)$
to
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
, then notice that
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
, then notice that
![]() $\alpha $
maps S to
$\alpha $
maps S to
![]() ${\widetilde {S}}$
, because S and
${\widetilde {S}}$
, because S and
![]() ${\widetilde {S}}$
are the unique maximal elements of
${\widetilde {S}}$
are the unique maximal elements of
![]() $\Delta $
and
$\Delta $
and
![]() $\widetilde {\Delta }$
, respectively. In particular,
$\widetilde {\Delta }$
, respectively. In particular,
![]() $\mathrm {Aut}(\mathcal L,\Delta ,S)$
acts on S for every locality
$\mathrm {Aut}(\mathcal L,\Delta ,S)$
acts on S for every locality
![]() $(\mathcal L,\Delta ,S)$
.
$(\mathcal L,\Delta ,S)$
.
Lemma 2.21. Suppose that
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a projection from a locality
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a projection from a locality
![]() $(\mathcal L,\Delta ,S)$
to a locality
$(\mathcal L,\Delta ,S)$
to a locality
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
. Then the following hold:
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
. Then the following hold:
-
(a)
 $N_{\mathcal L}(R)\alpha =N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
for every
$N_{\mathcal L}(R)\alpha =N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
for every
 $R\leq S$
with
$R\leq S$
with
 $S\cap \ker (\alpha )\leq R$
.
$S\cap \ker (\alpha )\leq R$
. -
(b) The map
 $\alpha |_S\colon S\longrightarrow {\widetilde {S}}$
induces an epimorphism of fusion systems from
$\alpha |_S\colon S\longrightarrow {\widetilde {S}}$
induces an epimorphism of fusion systems from
 $\mathcal {F}_S(\mathcal L)$
to
$\mathcal {F}_S(\mathcal L)$
to
 $\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
.
$\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
. -
(c) If
 $\alpha $
is an isomorphism, then
$\alpha $
is an isomorphism, then
 ${\widetilde {S}}_{f\alpha }=S_f\alpha $
for every
${\widetilde {S}}_{f\alpha }=S_f\alpha $
for every
 $f\in \mathcal L$
.
$f\in \mathcal L$
.
Proof. For the proof of (a) let
![]() $T:=S\cap \ker (\alpha )\leq R\leq S$
. By [Reference Chermak7, Lemma 3.1(a)], T is strongly closed in
$T:=S\cap \ker (\alpha )\leq R\leq S$
. By [Reference Chermak7, Lemma 3.1(a)], T is strongly closed in
![]() $\mathcal {F}_S(\mathcal L)$
. Clearly,
$\mathcal {F}_S(\mathcal L)$
. Clearly,
![]() $N_{\mathcal L}(R)\alpha \subseteq N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
. Let
$N_{\mathcal L}(R)\alpha \subseteq N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
. Let
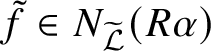 ${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
and write P for the full preimage of
${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(R\alpha )$
and write P for the full preimage of
![]() ${\widetilde {S}}_{{\tilde {f}}}$
in S. Then
${\widetilde {S}}_{{\tilde {f}}}$
in S. Then
![]() $T\leq R\leq P$
and
$T\leq R\leq P$
and
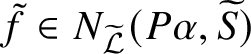 ${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(P\alpha ,{\widetilde {S}})$
. Hence, by [Reference Chermak7, Theorem 4.3(c)], we may choose
${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(P\alpha ,{\widetilde {S}})$
. Hence, by [Reference Chermak7, Theorem 4.3(c)], we may choose
![]() $f\in N_{\mathcal L}(P,S)$
with
$f\in N_{\mathcal L}(P,S)$
with
![]() $f\alpha ={\tilde {f}}$
. Then
$f\alpha ={\tilde {f}}$
. Then
![]() $R^f\leq S$
and
$R^f\leq S$
and
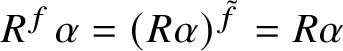 $R^f\alpha =(R\alpha )^{{\tilde {f}}}=R\alpha $
. So
$R^f\alpha =(R\alpha )^{{\tilde {f}}}=R\alpha $
. So
![]() $R^f=R$
because
$R^f=R$
because
![]() $T=T^f\leq R\cap R^f$
. Hence, we have shown that
$T=T^f\leq R\cap R^f$
. Hence, we have shown that
![]() $f\in N_{\mathcal L}(R)$
and thus that
$f\in N_{\mathcal L}(R)$
and thus that
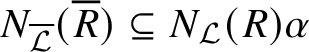 $N_{\overline {\mathcal L}}(\overline {R})\subseteq N_{\mathcal L}(R)\alpha $
. This proves (a).
$N_{\overline {\mathcal L}}(\overline {R})\subseteq N_{\mathcal L}(R)\alpha $
. This proves (a).
The fusion system
![]() $\mathcal {F}_S(\mathcal L)$
is generated by maps of the form
$\mathcal {F}_S(\mathcal L)$
is generated by maps of the form
![]() $c_f\colon P\longrightarrow Q$
, where
$c_f\colon P\longrightarrow Q$
, where
![]() $P,Q\in \Delta $
and
$P,Q\in \Delta $
and
![]() $f\in N_{\mathcal L}(P,Q)$
. Similarly,
$f\in N_{\mathcal L}(P,Q)$
. Similarly,
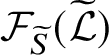 $\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
is generated by maps of the form
$\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
is generated by maps of the form
![]() $c_{{\tilde {f}}}\colon P\alpha \longrightarrow Q\alpha $
where
$c_{{\tilde {f}}}\colon P\alpha \longrightarrow Q\alpha $
where
![]() $P,Q\in \Delta $
and
$P,Q\in \Delta $
and
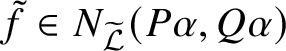 ${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(P\alpha ,Q\alpha )$
. Fixing
${\tilde {f}}\in N_{{\widetilde {\mathcal {L}}}}(P\alpha ,Q\alpha )$
. Fixing
![]() $P,Q\in \Delta $
, by [Reference Chermak7, Theorem 4.3(c)],
$P,Q\in \Delta $
, by [Reference Chermak7, Theorem 4.3(c)],
![]() $\alpha $
induces a surjection
$\alpha $
induces a surjection
![]() $N_{\mathcal L}(P,Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(P\alpha ,Q\alpha )$
. Moreover, if
$N_{\mathcal L}(P,Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(P\alpha ,Q\alpha )$
. Moreover, if
![]() $f\in N_{\mathcal L}(P,Q)$
, then
$f\in N_{\mathcal L}(P,Q)$
, then
![]() $(c_f|_P)(\alpha |_Q)=(\alpha |_P)(c_{f\alpha }|_{P\alpha })$
. This implies (b).
$(c_f|_P)(\alpha |_Q)=(\alpha |_P)(c_{f\alpha }|_{P\alpha })$
. This implies (b).
For the proof of (c), let
![]() $f\in \mathcal L$
be arbitrary and suppose that
$f\in \mathcal L$
be arbitrary and suppose that
![]() $\alpha $
is an isomorphism. Using that
$\alpha $
is an isomorphism. Using that
![]() $\alpha $
maps S isomorphically to
$\alpha $
maps S isomorphically to
![]() ${\widetilde {S}}$
and that
${\widetilde {S}}$
and that
![]() $(f^{-1})\alpha =(f\alpha )^{-1}$
by [Reference Chermak7, Lemma 1.13], we see
$(f^{-1})\alpha =(f\alpha )^{-1}$
by [Reference Chermak7, Lemma 1.13], we see
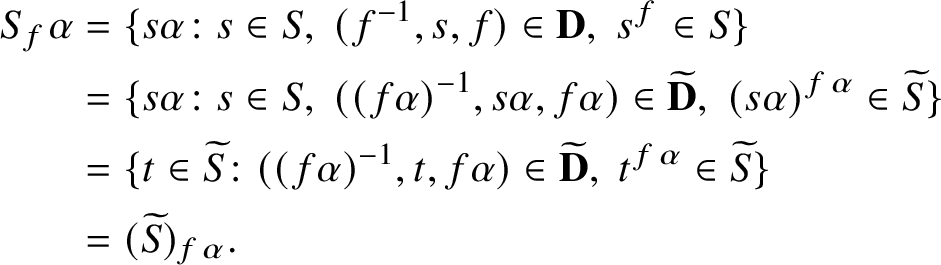 $$ \begin{align*} S_f\alpha&=\{s\alpha\colon s\in S,\;(f^{-1},s,f)\in\mathbf{D},\;s^f\in S\}\\ &=\{s\alpha\colon s\in S,\;((f\alpha)^{-1},s\alpha,f\alpha)\in\widetilde{\mathbf{D}},\;(s\alpha)^{f\alpha}\in {\widetilde{S}}\}\\ &=\{t\in {\widetilde{S}}\colon ((f\alpha)^{-1},t,f\alpha)\in\widetilde{\mathbf{D}},\;t^{f\alpha}\in {\widetilde{S}}\}\\ &= ({\widetilde{S}})_{f\alpha}.\\[-3.3pc] \end{align*} $$
$$ \begin{align*} S_f\alpha&=\{s\alpha\colon s\in S,\;(f^{-1},s,f)\in\mathbf{D},\;s^f\in S\}\\ &=\{s\alpha\colon s\in S,\;((f\alpha)^{-1},s\alpha,f\alpha)\in\widetilde{\mathbf{D}},\;(s\alpha)^{f\alpha}\in {\widetilde{S}}\}\\ &=\{t\in {\widetilde{S}}\colon ((f\alpha)^{-1},t,f\alpha)\in\widetilde{\mathbf{D}},\;t^{f\alpha}\in {\widetilde{S}}\}\\ &= ({\widetilde{S}})_{f\alpha}.\\[-3.3pc] \end{align*} $$
2.6. Restrictions of localities
Definition 2.22. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
be a locality with partial product
$(\mathcal L^+,\Delta ^+,S)$
be a locality with partial product
![]() $\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
, and let
$\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
, and let
![]() $\Delta \subseteq \Delta ^+$
be closed with respect to taking
$\Delta \subseteq \Delta ^+$
be closed with respect to taking
![]() $\mathcal L^+$
-conjugates and overgroups in S. Suppose that
$\mathcal L^+$
-conjugates and overgroups in S. Suppose that
![]() $\Delta $
is nonempty. Then we set
$\Delta $
is nonempty. Then we set
Note that
![]() $\mathbf {D}:=\mathbf {D}_{\Delta }(\mathcal L^+,\Pi ^+)\subseteq \mathbf {D}^+\cap \mathbf {W}(\mathcal L^+|_{\Delta })$
and, by Lemma 2.7(c),
$\mathbf {D}:=\mathbf {D}_{\Delta }(\mathcal L^+,\Pi ^+)\subseteq \mathbf {D}^+\cap \mathbf {W}(\mathcal L^+|_{\Delta })$
and, by Lemma 2.7(c),
![]() $\Pi ^+(w)\in \mathcal L|_{\Delta }$
for all
$\Pi ^+(w)\in \mathcal L|_{\Delta }$
for all
![]() $w\in \mathbf {D}$
. We call
$w\in \mathbf {D}$
. We call
![]() $\mathcal L:=\mathcal L^+|_{\Delta }$
together with the partial product
$\mathcal L:=\mathcal L^+|_{\Delta }$
together with the partial product
![]() $\Pi ^+|_{\mathbf {D}}\colon \mathbf {D}\longrightarrow \mathcal L$
and the restriction of the inversion map on
$\Pi ^+|_{\mathbf {D}}\colon \mathbf {D}\longrightarrow \mathcal L$
and the restriction of the inversion map on
![]() $\mathcal L^+$
to
$\mathcal L^+$
to
![]() $\mathcal L$
the restriction of
$\mathcal L$
the restriction of
![]() $\mathcal L^+$
to
$\mathcal L^+$
to
![]() $\Delta $
.
$\Delta $
.
The properties of the restriction
![]() $\mathcal L^+|_\Delta $
are summarised in the following lemma, which we will use throughout, most of the time without reference.
$\mathcal L^+|_\Delta $
are summarised in the following lemma, which we will use throughout, most of the time without reference.
Lemma 2.23. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
be a locality with partial product
$(\mathcal L^+,\Delta ^+,S)$
be a locality with partial product
![]() $\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
, and let
$\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
, and let
![]() $\Delta \subseteq \Delta ^+$
be nonempty and closed with respect to taking
$\Delta \subseteq \Delta ^+$
be nonempty and closed with respect to taking
![]() $\mathcal L^+$
-conjugates and overgroups in S. Set
$\mathcal L^+$
-conjugates and overgroups in S. Set
![]() $\mathcal L:=\mathcal L^+|_\Delta $
,
$\mathcal L:=\mathcal L^+|_\Delta $
,
![]() $\mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
and
$\mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
and
![]() $\Pi :=\Pi ^+|_{\mathbf {D}}$
.
$\Pi :=\Pi ^+|_{\mathbf {D}}$
.
-
(a)
 $\mathcal L$
together with
$\mathcal L$
together with
 $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and the restriction of the inversion map on
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and the restriction of the inversion map on
 $\mathcal L^+$
to
$\mathcal L^+$
to
 $\mathcal L$
forms a partial group.
$\mathcal L$
forms a partial group. -
(b) If
 $f\in \mathcal L$
, then it does not matter whether we form
$f\in \mathcal L$
, then it does not matter whether we form
 $S_f$
inside of
$S_f$
inside of
 $\mathcal L$
or of
$\mathcal L$
or of
 ${\mathcal L}^+$
; that is,
${\mathcal L}^+$
; that is,
 $S_f^{\mathcal L}=S_f^{\mathcal L^+}$
(with the notation introduced in Definition 2.4).
$S_f^{\mathcal L}=S_f^{\mathcal L^+}$
(with the notation introduced in Definition 2.4). -
(c) The triple
 $(\mathcal L,\Delta ,S)$
is a locality.
$(\mathcal L,\Delta ,S)$
is a locality.
Proof. Part (a) is straightforward to check. Let
![]() $f\in \mathcal L$
. Because
$f\in \mathcal L$
. Because
![]() $\mathbf {D}\subseteq \mathbf {D}^+$
and
$\mathbf {D}\subseteq \mathbf {D}^+$
and
![]() $\Pi =\Pi ^+|_{\mathbf {D}}$
, clearly
$\Pi =\Pi ^+|_{\mathbf {D}}$
, clearly
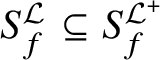 $S_f^{\mathcal L}\subseteq S_f^{\mathcal L^+}$
. Setting
$S_f^{\mathcal L}\subseteq S_f^{\mathcal L^+}$
. Setting
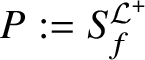 $P:=S_f^{\mathcal L^+}$
, by definition of
$P:=S_f^{\mathcal L^+}$
, by definition of
![]() $\mathcal L|_\Delta $
, we have
$\mathcal L|_\Delta $
, we have
![]() $P\in \Delta $
. Moreover, the conjugate
$P\in \Delta $
. Moreover, the conjugate
![]() $P^f$
is defined in
$P^f$
is defined in
![]() $\mathcal L^+$
and an element of
$\mathcal L^+$
and an element of
![]() $\Delta $
, because
$\Delta $
, because
![]() $\Delta $
is closed under taking
$\Delta $
is closed under taking
![]() $\mathcal L$
-conjugates. Now for
$\mathcal L$
-conjugates. Now for
![]() $a\in P$
, we have
$a\in P$
, we have
![]() $(f^{-1},a,f)\in \mathbf {D}=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
via
$(f^{-1},a,f)\in \mathbf {D}=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
via
![]() $P^f,P,P,P^f$
. Hence,
$P^f,P,P,P^f$
. Hence,
![]() $P^f$
is defined in
$P^f$
is defined in
![]() $\mathcal L$
, which implies
$\mathcal L$
, which implies
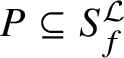 $P\subseteq S_f^{\mathcal L}$
. This shows (b).
$P\subseteq S_f^{\mathcal L}$
. This shows (b).
The proof of (c) is given in [Reference Chermak6, Lemma 2.21(a)], but we repeat the argument here in detail, because we feel that there is a small gap in the proof: Note that
![]() $S\in \Delta $
and so
$S\in \Delta $
and so
![]() $\mathbf {W}(S)\subseteq \mathbf {W}(N_{\mathcal L}(S))\subseteq \mathbf {D}=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
. Hence, S is a p-subgroup of
$\mathbf {W}(S)\subseteq \mathbf {W}(N_{\mathcal L}(S))\subseteq \mathbf {D}=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
. Hence, S is a p-subgroup of
![]() $\mathcal L$
. Because
$\mathcal L$
. Because
![]() $\mathbf {D}\subseteq \mathbf {D}^+$
and
$\mathbf {D}\subseteq \mathbf {D}^+$
and
![]() $\Pi =\Pi ^+|_{\mathbf {D}}$
, every p-subgroup of
$\Pi =\Pi ^+|_{\mathbf {D}}$
, every p-subgroup of
![]() $\mathcal L$
is also a p-subgroup of
$\mathcal L$
is also a p-subgroup of
![]() $\mathcal L^+$
. Therefore, S is a maximal p-subgroup of
$\mathcal L^+$
. Therefore, S is a maximal p-subgroup of
![]() $\mathcal L$
, because it is a maximal p-subgroup of
$\mathcal L$
, because it is a maximal p-subgroup of
![]() $\mathcal L^+$
. By assumption,
$\mathcal L^+$
. By assumption,
![]() $\Delta $
is closed under taking
$\Delta $
is closed under taking
![]() $\mathcal L^+$
-conjugates and overgroups in S, so it is in particular closed under taking
$\mathcal L^+$
-conjugates and overgroups in S, so it is in particular closed under taking
![]() $\mathcal L$
-conjugates in S. Thus, it remains to show that
$\mathcal L$
-conjugates in S. Thus, it remains to show that
![]() $\mathbf {D}_\Delta (\mathcal L,\Pi )=\mathbf {D}$
. Clearly,
$\mathbf {D}_\Delta (\mathcal L,\Pi )=\mathbf {D}$
. Clearly,
![]() $\mathbf {D}_\Delta (\mathcal L,\Pi )\subseteq \mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
. If
$\mathbf {D}_\Delta (\mathcal L,\Pi )\subseteq \mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
. If
![]() $w=(f_1,\dots ,f_n)\in \mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
via
$w=(f_1,\dots ,f_n)\in \mathbf {D}:=\mathbf {D}_\Delta (\mathcal L^+,\Pi ^+)$
via
![]() $P_0,\dots ,P_n\in \Delta $
, this means that the conjugate
$P_0,\dots ,P_n\in \Delta $
, this means that the conjugate
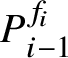 $P_{i-1}^{f_i}$
is defined in
$P_{i-1}^{f_i}$
is defined in
![]() $\mathcal L^+$
and equal to
$\mathcal L^+$
and equal to
![]() $P_i$
for
$P_i$
for
![]() $i=1,\dots ,n$
. Then
$i=1,\dots ,n$
. Then
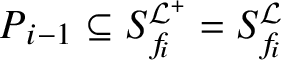 $P_{i-1}\subseteq S_{f_i}^{\mathcal L^+}=S_{f_i}^{\mathcal L}$
by (b). Hence,
$P_{i-1}\subseteq S_{f_i}^{\mathcal L^+}=S_{f_i}^{\mathcal L}$
by (b). Hence,
![]() $w\in \mathbf {D}_\Delta (\mathcal L,\Pi )$
via
$w\in \mathbf {D}_\Delta (\mathcal L,\Pi )$
via
![]() $P_0,P_1,\dots ,P_n$
. This proves (c).
$P_0,P_1,\dots ,P_n$
. This proves (c).
Lemma 2.24. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
and
$(\mathcal L^+,\Delta ^+,S)$
and
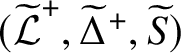 $({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}})$
be localities. Let
$({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}})$
be localities. Let
![]() $\emptyset \neq \Delta \subseteq \Delta ^+$
and
$\emptyset \neq \Delta \subseteq \Delta ^+$
and
![]() $\emptyset \neq \widetilde {\Delta }\subseteq \widetilde {\Delta }^+$
such that
$\emptyset \neq \widetilde {\Delta }\subseteq \widetilde {\Delta }^+$
such that
![]() $\Delta $
is closed under taking
$\Delta $
is closed under taking
![]() $\mathcal L^+$
-conjugates and overgroups in S and
$\mathcal L^+$
-conjugates and overgroups in S and
![]() $\widetilde {\Delta }$
is closed under taking
$\widetilde {\Delta }$
is closed under taking
![]() ${\widetilde {\mathcal {L}}}$
-conjugates and overgroups in
${\widetilde {\mathcal {L}}}$
-conjugates and overgroups in
![]() ${\widetilde {S}}$
. Set
${\widetilde {S}}$
. Set
![]() $\mathcal L:=\mathcal L^+|_{\Delta }$
and
$\mathcal L:=\mathcal L^+|_{\Delta }$
and
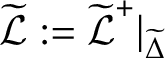 ${\widetilde {\mathcal {L}}}:={\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }}$
. Then
${\widetilde {\mathcal {L}}}:={\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }}$
. Then
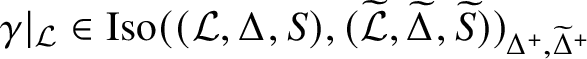 $\gamma |_{\mathcal L}\in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
for every
$\gamma |_{\mathcal L}\in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
for every
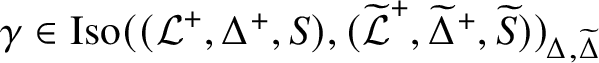 $\gamma \in \mathrm {Iso}((\mathcal L^+,\Delta ^+,S),({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}}))_{\Delta ,\widetilde {\Delta }}$
.
$\gamma \in \mathrm {Iso}((\mathcal L^+,\Delta ^+,S),({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}}))_{\Delta ,\widetilde {\Delta }}$
.
Proof. If
![]() $f\in \mathcal L^+$
, then by Lemma 2.21(c),
$f\in \mathcal L^+$
, then by Lemma 2.21(c),
 ${\widetilde {S}}_{f\gamma }=S_f\gamma $
. Because
${\widetilde {S}}_{f\gamma }=S_f\gamma $
. Because
![]() $\Delta \gamma =\widetilde {\Delta }$
and
$\Delta \gamma =\widetilde {\Delta }$
and
![]() $\gamma $
is bijective, this means that
$\gamma $
is bijective, this means that
![]() $S_f\in \Delta $
if and only if
$S_f\in \Delta $
if and only if
 ${\widetilde {S}}_{f\gamma }\in \widetilde {\Delta }$
. Hence,
${\widetilde {S}}_{f\gamma }\in \widetilde {\Delta }$
. Hence,
![]() $f\in \mathcal L$
if and only if
$f\in \mathcal L$
if and only if
![]() $f\gamma \in {\widetilde {\mathcal {L}}}$
; that is,
$f\gamma \in {\widetilde {\mathcal {L}}}$
; that is,
![]() $\gamma |_{\mathcal L}\colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is well defined and surjective. Clearly,
$\gamma |_{\mathcal L}\colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is well defined and surjective. Clearly,
![]() $\gamma |_{\mathcal L}$
is injective.
$\gamma |_{\mathcal L}$
is injective.
Write
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
![]() $\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\rightarrow {\widetilde {\mathcal {L}}}$
for the products on
$\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\rightarrow {\widetilde {\mathcal {L}}}$
for the products on
![]() $\mathcal L$
and
$\mathcal L$
and
![]() ${\widetilde {\mathcal {L}}}$
, respectively. Let
${\widetilde {\mathcal {L}}}$
, respectively. Let
![]() $w=(f_1,\dots ,f_n)\in \mathbf {D}$
via
$w=(f_1,\dots ,f_n)\in \mathbf {D}$
via
![]() $P_0,\dots ,P_n\in \Delta $
; that is,
$P_0,\dots ,P_n\in \Delta $
; that is,
![]() $P_{i-1}\leq S_{f_i}$
and
$P_{i-1}\leq S_{f_i}$
and
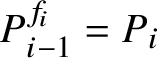 $P_{i-1}^{f_i}=P_i$
for
$P_{i-1}^{f_i}=P_i$
for
![]() $i=1,\dots ,n$
. Then
$i=1,\dots ,n$
. Then
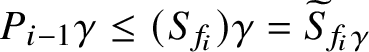 $P_{i-1}\gamma \leq (S_{f_i})\gamma ={\widetilde {S}}_{f_i\gamma }$
and, because
$P_{i-1}\gamma \leq (S_{f_i})\gamma ={\widetilde {S}}_{f_i\gamma }$
and, because
![]() $\gamma $
is a homomorphism of partial groups,
$\gamma $
is a homomorphism of partial groups,
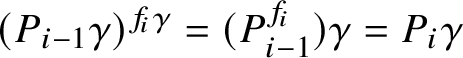 $(P_{i-1}\gamma )^{f_i\gamma }=(P_{i-1}^{f_i})\gamma =P_i\gamma $
. Because
$(P_{i-1}\gamma )^{f_i\gamma }=(P_{i-1}^{f_i})\gamma =P_i\gamma $
. Because
![]() $\Delta \gamma =\widetilde {\Delta }$
, this shows that
$\Delta \gamma =\widetilde {\Delta }$
, this shows that
![]() $w\gamma ^*=(f_1\gamma ,\dots ,f_n\gamma )\in \widetilde {\mathbf {D}}$
via
$w\gamma ^*=(f_1\gamma ,\dots ,f_n\gamma )\in \widetilde {\mathbf {D}}$
via
![]() $P_0\gamma ,\dots ,P_n\gamma \in \widetilde {\Delta }$
. Hence,
$P_0\gamma ,\dots ,P_n\gamma \in \widetilde {\Delta }$
. Hence,
![]() $\mathbf {D}\gamma ^*\subseteq \widetilde {\mathbf {D}}$
. Because
$\mathbf {D}\gamma ^*\subseteq \widetilde {\mathbf {D}}$
. Because
![]() $\gamma ^{-1}$
is an isomorphism from
$\gamma ^{-1}$
is an isomorphism from
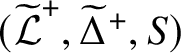 $({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,S)$
to
$({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,S)$
to
![]() $(\mathcal L^+,\Delta ^+,S)$
by Lemma 2.18, a symmetric argument shows that
$(\mathcal L^+,\Delta ^+,S)$
by Lemma 2.18, a symmetric argument shows that
![]() $\widetilde {\mathbf {D}}(\gamma ^{-1})^*\subseteq \mathbf {D}$
and thus
$\widetilde {\mathbf {D}}(\gamma ^{-1})^*\subseteq \mathbf {D}$
and thus
![]() $\widetilde {\mathbf {D}}\subseteq \mathbf {D}\gamma ^*$
. This proves
$\widetilde {\mathbf {D}}\subseteq \mathbf {D}\gamma ^*$
. This proves
![]() $\mathbf {D}\gamma ^*=\widetilde {\mathbf {D}}$
. Because
$\mathbf {D}\gamma ^*=\widetilde {\mathbf {D}}$
. Because
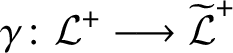 $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
is a homomorphism of partial groups and because
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
is a homomorphism of partial groups and because
![]() $\Pi $
and
$\Pi $
and
![]() $\widetilde {\Pi }$
are restrictions of the products on
$\widetilde {\Pi }$
are restrictions of the products on
![]() $\mathcal L^+$
and
$\mathcal L^+$
and
![]() ${\widetilde {\mathcal {L}}}^+$
, respectively, we have
${\widetilde {\mathcal {L}}}^+$
, respectively, we have
![]() $\widetilde {\Pi }(w\gamma ^*)=\Pi (w)\gamma $
for all
$\widetilde {\Pi }(w\gamma ^*)=\Pi (w)\gamma $
for all
![]() $w\in \mathbf {D}$
. So
$w\in \mathbf {D}$
. So
![]() $\gamma |_{\mathcal L}$
is an isomorphism of partial groups from
$\gamma |_{\mathcal L}$
is an isomorphism of partial groups from
![]() $\mathcal L$
to
$\mathcal L$
to
![]() ${\widetilde {\mathcal {L}}}$
and the assertion follows.
${\widetilde {\mathcal {L}}}$
and the assertion follows.
2.7. Linking localities
Definition 2.25.
-
• A finite group G is said to be of characteristic p of
 $C_G(O_p(G))\leq O_p(G)$
.
$C_G(O_p(G))\leq O_p(G)$
. -
• A locality
 $(\mathcal L,\Delta ,S)$
is called a linking locality if
$(\mathcal L,\Delta ,S)$
is called a linking locality if
 $\mathcal {F}_S(\mathcal L)$
is saturated,
$\mathcal {F}_S(\mathcal L)$
is saturated,
 $N_{\mathcal L}(P)$
is of characteristic p for every
$N_{\mathcal L}(P)$
is of characteristic p for every
 $P \in \Delta $
and
$P \in \Delta $
and
 $\mathcal {F}_S(\mathcal L)^{cr}\subseteq \Delta $
.
$\mathcal {F}_S(\mathcal L)^{cr}\subseteq \Delta $
. -
• If
 $\mathcal {F}$
is a saturated fusion system over a p-group S, then a subgroup
$\mathcal {F}$
is a saturated fusion system over a p-group S, then a subgroup
 $P\leq S$
is called
$P\leq S$
is called
 $\mathcal {F}$
-subcentric if
$\mathcal {F}$
-subcentric if
 $N_{\mathcal {F}}(Q)$
is constrained for every fully
$N_{\mathcal {F}}(Q)$
is constrained for every fully
 $\mathcal {F}$
-normalised
$\mathcal {F}$
-normalised
 $\mathcal {F}$
-conjugate Q of P. Write
$\mathcal {F}$
-conjugate Q of P. Write
 $\mathcal {F}^s$
for the set of
$\mathcal {F}^s$
for the set of
 $\mathcal {F}$
-subcentric subgroups of S.
$\mathcal {F}$
-subcentric subgroups of S. -
• A subcentric linking locality is a linking locality
 $(\mathcal L,\Delta ,S)$
such that
$(\mathcal L,\Delta ,S)$
such that
 $\Delta =\mathcal {F}_S(\mathcal L)^s$
.
$\Delta =\mathcal {F}_S(\mathcal L)^s$
.
Linking localities are closely related to linking systems. We provide some more details on that in Subsection 4.3. Given a saturated fusion system
![]() $\mathcal {F}$
, it is elementary to show that the object set
$\mathcal {F}$
, it is elementary to show that the object set
![]() $\Delta $
of a linking locality over
$\Delta $
of a linking locality over
![]() $\mathcal {F}$
is always contained in
$\mathcal {F}$
is always contained in
![]() $\mathcal {F}^s$
. On the other hand, using the existence and uniqueness of centric linking systems, it is shown in [Reference Henke14, Theorem A] that, for every
$\mathcal {F}^s$
. On the other hand, using the existence and uniqueness of centric linking systems, it is shown in [Reference Henke14, Theorem A] that, for every
![]() $\mathcal {F}$
-closed set
$\mathcal {F}$
-closed set
![]() $\Delta $
with
$\Delta $
with
![]() $\mathcal {F}^{cr}\subseteq \Delta \subseteq \mathcal {F}^s$
, there exists a linking locality
$\mathcal {F}^{cr}\subseteq \Delta \subseteq \mathcal {F}^s$
, there exists a linking locality
![]() $(\mathcal L,\Delta ,S)$
over
$(\mathcal L,\Delta ,S)$
over
![]() $\mathcal {F}$
that is unique up to rigid isomorphism. Moreover, it is proved that the set
$\mathcal {F}$
that is unique up to rigid isomorphism. Moreover, it is proved that the set
![]() $\mathcal {F}^s$
is
$\mathcal {F}^s$
is
![]() $\mathcal {F}$
-closed and thus there exists a subcentric linking locality over
$\mathcal {F}$
-closed and thus there exists a subcentric linking locality over
![]() $\mathcal {F}$
that is unique up to rigid isomorphism.
$\mathcal {F}$
that is unique up to rigid isomorphism.
We will need the following slightly technical lemma.
Lemma 2.26. Suppose that
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
. Let
$\mathcal L=\mathcal L^+|_\Delta $
. Let
![]() $R\in \Delta ^+\backslash \Delta $
such that R is fully normalised and every proper overgroup of R is in
$R\in \Delta ^+\backslash \Delta $
such that R is fully normalised and every proper overgroup of R is in
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of R. Moreover,
$N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of R. Moreover,
![]() $R^*=O_p(N_{\mathcal L^+}(R))\in \Delta $
and
$R^*=O_p(N_{\mathcal L^+}(R))\in \Delta $
and
![]() $N_{\mathcal L}(R)=N_{N_{\mathcal L}(R^*)}(R)$
.
$N_{\mathcal L}(R)=N_{N_{\mathcal L}(R^*)}(R)$
.
Proof. Because
![]() $R\not \in \Delta $
and
$R\not \in \Delta $
and
![]() $\mathcal {F}^{cr}\subseteq \Delta $
, we have
$\mathcal {F}^{cr}\subseteq \Delta $
, we have
![]() $R\not \in \mathcal {F}^{cr}$
. By [Reference Henke14, Lemma 6.2], this implies
$R\not \in \mathcal {F}^{cr}$
. By [Reference Henke14, Lemma 6.2], this implies
![]() $R<R^*:=O_p(N_{\mathcal L^+}(R))$
and so
$R<R^*:=O_p(N_{\mathcal L^+}(R))$
and so
![]() $R^*\in \Delta $
. Hence, using Lemma 2.23(b), we see that
$R^*\in \Delta $
. Hence, using Lemma 2.23(b), we see that
![]() $N_{\mathcal L^+}(R)\subseteq N_{\mathcal L^+}(R^*)=N_{\mathcal L}(R^*)$
and
$N_{\mathcal L^+}(R)\subseteq N_{\mathcal L^+}(R^*)=N_{\mathcal L}(R^*)$
and
![]() $N_{\mathcal L^+}(R)=N_{N_{\mathcal L^+}(R^*)}(R)=N_{N_{\mathcal L}(R^*)}(R)=N_{\mathcal L}(R)$
is a subgroup of
$N_{\mathcal L^+}(R)=N_{N_{\mathcal L^+}(R^*)}(R)=N_{N_{\mathcal L}(R^*)}(R)=N_{\mathcal L}(R)$
is a subgroup of
![]() $\mathcal L$
.
$\mathcal L$
.
3. A crucial lemma
In this section we prove the following general lemma on which the proofs of Theorem A.1 and Theorem C will be based. It is also used in Reference Chermak and Henke[10] to show that there is a one-to-one correspondence between the normal subsystems of a saturated fusion system and the partial normal subgroups of an associated linking locality.
Lemma 3.1. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
and
$(\mathcal L^+,\Delta ^+,S)$
and
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
be localities, set
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
be localities, set
![]() $\mathcal {F}:=\mathcal {F}_S(\mathcal L^+)$
and let
$\mathcal {F}:=\mathcal {F}_S(\mathcal L^+)$
and let
![]() $\Delta $
be a nonempty subset of
$\Delta $
be a nonempty subset of
![]() $\Delta ^+$
that is
$\Delta ^+$
that is
![]() $\mathcal {F}$
-closed. Set
$\mathcal {F}$
-closed. Set
![]() $\mathcal L:=\mathcal L^+|_\Delta $
. Let T be a strongly
$\mathcal L:=\mathcal L^+|_\Delta $
. Let T be a strongly
![]() $\mathcal {F}$
-closed subgroup such that
$\mathcal {F}$
-closed subgroup such that
Assume that every proper overgroup in T of an element of
![]() $\Gamma ^+\backslash \Gamma $
is in
$\Gamma ^+\backslash \Gamma $
is in
![]() $\Gamma $
. Suppose we are given
$\Gamma $
. Suppose we are given
-
• a homomorphism of partial groups
 $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
 $\Delta ^+\alpha \subseteq \widetilde {\Delta }$
;
$\Delta ^+\alpha \subseteq \widetilde {\Delta }$
; -
• a set
 $\Gamma _0\subseteq \Gamma ^+\backslash \Gamma $
of fully
$\Gamma _0\subseteq \Gamma ^+\backslash \Gamma $
of fully
 $\mathcal {F}$
-normalised representatives of the
$\mathcal {F}$
-normalised representatives of the
 $\mathcal {F}$
-conjugacy classes of the subgroups in
$\mathcal {F}$
-conjugacy classes of the subgroups in
 $\Gamma ^+\backslash \Gamma $
; and
$\Gamma ^+\backslash \Gamma $
; and -
• for each
 $Q\in \Gamma _0$
a homomorphism of groups
$Q\in \Gamma _0$
a homomorphism of groups
 $\alpha _Q\colon N_{\mathcal L^+}(Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
with
$\alpha _Q\colon N_{\mathcal L^+}(Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
with
 $\alpha _Q|_{N_{\mathcal L}(Q)}=\alpha |_{N_{\mathcal L}(Q)}$
.
$\alpha _Q|_{N_{\mathcal L}(Q)}=\alpha |_{N_{\mathcal L}(Q)}$
.
Then there exists a unique homomorphism of partial groups
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\gamma |_{\mathcal L}=\alpha $
and
$\gamma |_{\mathcal L}=\alpha $
and
![]() $\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
$\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
![]() $Q\in \Gamma _0$
.
$Q\in \Gamma _0$
.
Proof. Write
![]() $\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
,
$\Pi ^+\colon \mathbf {D}^+\longrightarrow \mathcal L^+$
,
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L$
and
![]() $\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\longrightarrow {\widetilde {\mathcal {L}}}$
for the partial products on
$\widetilde {\Pi }\colon \widetilde {\mathbf {D}}\longrightarrow {\widetilde {\mathcal {L}}}$
for the partial products on
![]() $\mathcal L^+$
,
$\mathcal L^+$
,
![]() $\mathcal L$
and
$\mathcal L$
and
![]() ${\widetilde {\mathcal {L}}}$
, respectively. Recall from Definition 2.22 that then
${\widetilde {\mathcal {L}}}$
, respectively. Recall from Definition 2.22 that then
![]() $\mathbf {D}\subseteq \mathbf {D}^+$
and
$\mathbf {D}\subseteq \mathbf {D}^+$
and
![]() $\Pi =\Pi ^+|_{\mathbf {D}}$
. Because
$\Pi =\Pi ^+|_{\mathbf {D}}$
. Because
![]() $\Gamma _0$
is a set of representatives of the
$\Gamma _0$
is a set of representatives of the
![]() $\mathcal {F}$
-conjugacy classes of subgroups in
$\mathcal {F}$
-conjugacy classes of subgroups in
![]() $\Gamma ^+\backslash \Gamma $
, for every
$\Gamma ^+\backslash \Gamma $
, for every
![]() $P\in \Gamma ^+\backslash \Gamma $
there is a unique element of
$P\in \Gamma ^+\backslash \Gamma $
there is a unique element of
![]() $\Gamma _0\cap P^{\mathcal {F}}$
, which we denote by
$\Gamma _0\cap P^{\mathcal {F}}$
, which we denote by
![]() $Q_P$
. By Lemma 2.10(b), for every
$Q_P$
. By Lemma 2.10(b), for every
![]() $P\in \Gamma ^+\backslash \Gamma $
we may moreover pick
$P\in \Gamma ^+\backslash \Gamma $
we may moreover pick
![]() $h_P\in N_{\mathcal L^+}(N_S(P),S)$
with
$h_P\in N_{\mathcal L^+}(N_S(P),S)$
with
![]() $P^{h_P}=Q_P$
. Because
$P^{h_P}=Q_P$
. Because
![]() $S\in \Delta $
, we have
$S\in \Delta $
, we have
![]() $T\in \Gamma $
. So
$T\in \Gamma $
. So
![]() $P\neq T$
and thus
$P\neq T$
and thus
![]() $P<N_T(P)\in \Gamma $
by assumption. In particular,
$P<N_T(P)\in \Gamma $
by assumption. In particular,
![]() $N_S(P)\in \Delta $
,
$N_S(P)\in \Delta $
,
![]() $h_P\in N_{\mathcal L}(N_S(P),S)$
and the conjugate
$h_P\in N_{\mathcal L}(N_S(P),S)$
and the conjugate
![]() $P^{h_P}$
is defined in
$P^{h_P}$
is defined in
![]() $\mathcal L$
.
$\mathcal L$
.
We now first define a map
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
and show then that it has the required properties. If
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
and show then that it has the required properties. If
![]() $f\in \mathcal L$
, then we set
$f\in \mathcal L$
, then we set
![]() $f\gamma =f\alpha $
. Suppose now that
$f\gamma =f\alpha $
. Suppose now that
![]() $f\in \mathcal L^+\backslash \mathcal L$
so that
$f\in \mathcal L^+\backslash \mathcal L$
so that
![]() $S_f\in \Delta ^+\backslash \Delta $
and thus
$S_f\in \Delta ^+\backslash \Delta $
and thus
Notice that P and
![]() $P^f$
are
$P^f$
are
![]() $\mathcal {F}$
-conjugate and thus
$\mathcal {F}$
-conjugate and thus
![]() $Q:=Q_P=Q_{P^f}$
. Because
$Q:=Q_P=Q_{P^f}$
. Because
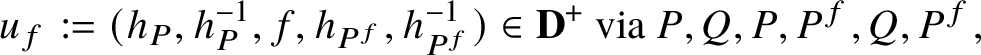 $$ \begin{align*}u_f:=(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})\in\mathbf{D}^+\mbox{ via }P,Q,P,P^f,Q,P^f,\end{align*} $$
$$ \begin{align*}u_f:=(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})\in\mathbf{D}^+\mbox{ via }P,Q,P,P^f,Q,P^f,\end{align*} $$
we have
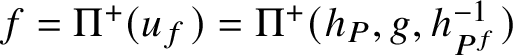 $f=\Pi ^+(u_f)=\Pi ^+(h_P,g,h_{P^f}^{-1})$
, where
$f=\Pi ^+(u_f)=\Pi ^+(h_P,g,h_{P^f}^{-1})$
, where
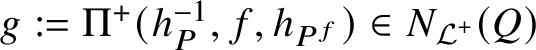 $g:=\Pi ^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L^+}(Q)$
. Observe that
$g:=\Pi ^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L^+}(Q)$
. Observe that
![]() $P^{h_P}=Q$
and
$P^{h_P}=Q$
and
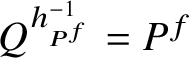 $Q^{h_{P^f}^{-1}}=P^f$
in
$Q^{h_{P^f}^{-1}}=P^f$
in
![]() $\mathcal L$
. Moreover,
$\mathcal L$
. Moreover,
Because
![]() $\Delta ^+\alpha \subseteq \widetilde {\Delta }$
and
$\Delta ^+\alpha \subseteq \widetilde {\Delta }$
and
![]() $\alpha $
is a homomorphism of partial groups, we conclude that
$\alpha $
is a homomorphism of partial groups, we conclude that
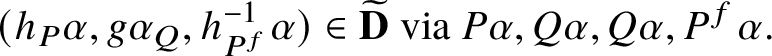 $$ \begin{align*}(h_P\alpha,g\alpha_Q,h_{P^f}^{-1}\alpha)\in \widetilde{\mathbf{D}}\mbox{ via }P\alpha,Q\alpha,Q\alpha,P^f\alpha.\end{align*} $$
$$ \begin{align*}(h_P\alpha,g\alpha_Q,h_{P^f}^{-1}\alpha)\in \widetilde{\mathbf{D}}\mbox{ via }P\alpha,Q\alpha,Q\alpha,P^f\alpha.\end{align*} $$
So for every
![]() $f\in \mathcal L^+\backslash \mathcal L$
, setting
$f\in \mathcal L^+\backslash \mathcal L$
, setting
![]() $P:=S_f\cap T$
and
$P:=S_f\cap T$
and
![]() $Q:=Q_P$
, we may define
$Q:=Q_P$
, we may define
![]() $f\gamma $
via
$f\gamma $
via
 $$ \begin{align} f\gamma=\widetilde{\Pi}(h_P\alpha,g\alpha_{Q},h_{P^f}^{-1}\alpha)\mbox{ where }g=\Pi^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L^+}(Q). \end{align} $$
$$ \begin{align} f\gamma=\widetilde{\Pi}(h_P\alpha,g\alpha_{Q},h_{P^f}^{-1}\alpha)\mbox{ where }g=\Pi^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L^+}(Q). \end{align} $$
If
![]() $\beta \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups with
$\beta \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups with
![]() $\beta |_{\mathcal L}=\alpha $
and
$\beta |_{\mathcal L}=\alpha $
and
![]() $\beta |_{N_{\mathcal L^+}(Q)}=\alpha _{Q}$
for all
$\beta |_{N_{\mathcal L^+}(Q)}=\alpha _{Q}$
for all
![]() $Q\in \Gamma _0$
, then with f, g, P and Q as above, we see that
$Q\in \Gamma _0$
, then with f, g, P and Q as above, we see that
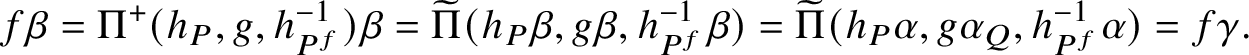 $$ \begin{align*}f\beta=\Pi^+(h_P,g,h_{P^f}^{-1})\beta=\widetilde{\Pi}(h_P\beta,g\beta,h_{P^f}^{-1}\beta)=\widetilde{\Pi}(h_P\alpha,g\alpha_{Q},h_{P^f}^{-1}\alpha)=f\gamma.\end{align*} $$
$$ \begin{align*}f\beta=\Pi^+(h_P,g,h_{P^f}^{-1})\beta=\widetilde{\Pi}(h_P\beta,g\beta,h_{P^f}^{-1}\beta)=\widetilde{\Pi}(h_P\alpha,g\alpha_{Q},h_{P^f}^{-1}\alpha)=f\gamma.\end{align*} $$
Hence, we have in this case
![]() $\beta =\gamma $
. So to prove the assertion, it is sufficient to show that
$\beta =\gamma $
. So to prove the assertion, it is sufficient to show that
![]() $\gamma $
is a homomorphism of partial groups with
$\gamma $
is a homomorphism of partial groups with
![]() $\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for all
$\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for all
![]() $Q\in \Gamma _0$
.
$Q\in \Gamma _0$
.
Step 1: Given
![]() $f\in \mathcal L^+$
and
$f\in \mathcal L^+$
and
![]() $P\in \Gamma ^+\backslash \Gamma $
with
$P\in \Gamma ^+\backslash \Gamma $
with
![]() $P\leq S_f\cap T$
, we show that (3.1.1) holds for
$P\leq S_f\cap T$
, we show that (3.1.1) holds for
![]() $Q:=Q_P$
. If
$Q:=Q_P$
. If
![]() $P=S_f\cap T$
, then
$P=S_f\cap T$
, then
![]() $S_f\not \in \Delta $
, so
$S_f\not \in \Delta $
, so
![]() $f\not \in \mathcal L$
and the equation holds by the definition of
$f\not \in \mathcal L$
and the equation holds by the definition of
![]() $\gamma $
.
$\gamma $
.
Assume now that
![]() $P<S_f\cap T$
. Then, by assumption,
$P<S_f\cap T$
. Then, by assumption,
![]() $S_f\cap T\in \Gamma $
and thus
$S_f\cap T\in \Gamma $
and thus
![]() $f\in \mathcal L$
. Moreover,
$f\in \mathcal L$
. Moreover,
![]() $P<R:=N_{S_f\cap T}(P)\in \Gamma $
. Notice that
$P<R:=N_{S_f\cap T}(P)\in \Gamma $
. Notice that
![]() $R\leq N_S(P)\leq S_{h_P}$
and
$R\leq N_S(P)\leq S_{h_P}$
and
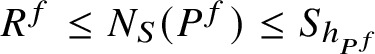 $R^f\leq N_S(P^f)\leq S_{h_{P^f}}$
. Hence,
$R^f\leq N_S(P^f)\leq S_{h_{P^f}}$
. Hence,
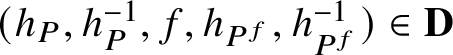 $(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})\in \mathbf {D}$
via R, and so
$(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})\in \mathbf {D}$
via R, and so
 $$ \begin{align*}f=\Pi(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})=\Pi(h_P,g,h_{P^f}^{-1}),\end{align*} $$
$$ \begin{align*}f=\Pi(h_P,h_P^{-1},f,h_{P^f},h_{P^f}^{-1})=\Pi(h_P,g,h_{P^f}^{-1}),\end{align*} $$
where
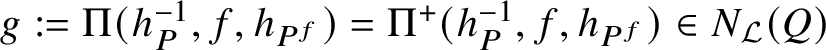 $g:=\Pi (h_P^{-1},f,h_{P^f})=\Pi ^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L}(Q)$
. Recall that
$g:=\Pi (h_P^{-1},f,h_{P^f})=\Pi ^+(h_P^{-1},f,h_{P^f})\in N_{\mathcal L}(Q)$
. Recall that
![]() $\gamma |_{\mathcal L}=\alpha $
by definition of
$\gamma |_{\mathcal L}=\alpha $
by definition of
![]() $\gamma $
. Because
$\gamma $
. Because
![]() $\alpha $
is a homomorphism of partial groups with
$\alpha $
is a homomorphism of partial groups with
![]() $\alpha |_{N_{\mathcal L}(Q)}=\alpha _Q|_{N_{\mathcal L}(Q)}$
, it follows that
$\alpha |_{N_{\mathcal L}(Q)}=\alpha _Q|_{N_{\mathcal L}(Q)}$
, it follows that
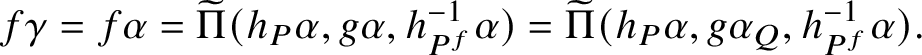 $$ \begin{align*}f\gamma=f\alpha=\widetilde{\Pi}(h_P\alpha,g\alpha,h_{P^f}^{-1}\alpha)=\widetilde{\Pi}(h_P\alpha,g\alpha_Q,h_{P^f}^{-1}\alpha).\end{align*} $$
$$ \begin{align*}f\gamma=f\alpha=\widetilde{\Pi}(h_P\alpha,g\alpha,h_{P^f}^{-1}\alpha)=\widetilde{\Pi}(h_P\alpha,g\alpha_Q,h_{P^f}^{-1}\alpha).\end{align*} $$
So (3.1.1) holds.
Step 2: We show that
![]() $\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
$\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
![]() $Q\in \Gamma _0$
. To prove this, fix
$Q\in \Gamma _0$
. To prove this, fix
![]() $Q\in \Gamma _0$
and
$Q\in \Gamma _0$
and
![]() $f\in N_{\mathcal L^+}(Q)$
. Observe that
$f\in N_{\mathcal L^+}(Q)$
. Observe that
![]() $h_Q\in N_{\mathcal L^+}(Q)$
and
$h_Q\in N_{\mathcal L^+}(Q)$
and
![]() $h_Q\alpha _Q\in N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Indeed,
$h_Q\alpha _Q\in N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Indeed,
![]() $h_Q\in N_{\mathcal L}(Q)$
and so
$h_Q\in N_{\mathcal L}(Q)$
and so
![]() $h_Q\alpha _Q=h_Q\alpha $
. By Step 1, we have
$h_Q\alpha _Q=h_Q\alpha $
. By Step 1, we have
 $$ \begin{align*}f\gamma=\widetilde{\Pi}(h_Q\alpha,g\alpha_{Q},h_Q^{-1}\alpha),\end{align*} $$
$$ \begin{align*}f\gamma=\widetilde{\Pi}(h_Q\alpha,g\alpha_{Q},h_Q^{-1}\alpha),\end{align*} $$
where
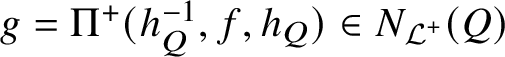 $g=\Pi ^+(h_Q^{-1},f,h_Q)\in N_{\mathcal L^+}(Q)$
. Moreover,
$g=\Pi ^+(h_Q^{-1},f,h_Q)\in N_{\mathcal L^+}(Q)$
. Moreover,
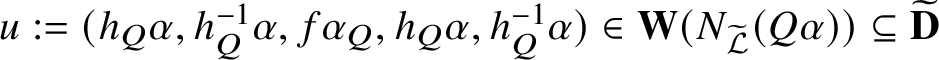 $u:=(h_Q\alpha ,h_Q^{-1}\alpha ,f\alpha _Q,h_Q\alpha ,h_Q^{-1}\alpha )\in \mathbf {W}(N_{{\widetilde {\mathcal {L}}}}(Q\alpha ))\subseteq \widetilde {\mathbf {D}}$
. Because
$u:=(h_Q\alpha ,h_Q^{-1}\alpha ,f\alpha _Q,h_Q\alpha ,h_Q^{-1}\alpha )\in \mathbf {W}(N_{{\widetilde {\mathcal {L}}}}(Q\alpha ))\subseteq \widetilde {\mathbf {D}}$
. Because
![]() $N_{\mathcal L^+}(Q)$
is a group,
$N_{\mathcal L^+}(Q)$
is a group,
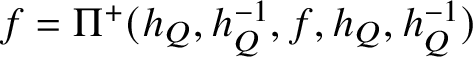 $f=\Pi ^+(h_Q,h_Q^{-1},f,h_Q,h_Q^{-1})$
. So
$f=\Pi ^+(h_Q,h_Q^{-1},f,h_Q,h_Q^{-1})$
. So
 $$ \begin{align*}f\alpha_Q=\widetilde{\Pi}(u)=\widetilde{\Pi}(h_Q\alpha,\widetilde{\Pi}(h_Q^{-1}\alpha,f\alpha_Q,h_Q\alpha),h_Q^{-1}\alpha)=\widetilde{\Pi}(h_Q\alpha,g\alpha_Q,h_Q^{-1}\alpha)=f\gamma,\end{align*} $$
$$ \begin{align*}f\alpha_Q=\widetilde{\Pi}(u)=\widetilde{\Pi}(h_Q\alpha,\widetilde{\Pi}(h_Q^{-1}\alpha,f\alpha_Q,h_Q\alpha),h_Q^{-1}\alpha)=\widetilde{\Pi}(h_Q\alpha,g\alpha_Q,h_Q^{-1}\alpha)=f\gamma,\end{align*} $$
where the third equality uses that
![]() $\alpha _Q$
is a homomorphism of groups with
$\alpha _Q$
is a homomorphism of groups with
![]() $h_Q\alpha _Q=h_Q\alpha $
and
$h_Q\alpha _Q=h_Q\alpha $
and
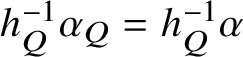 $h_Q^{-1}\alpha _Q=h_Q^{-1}\alpha $
.
$h_Q^{-1}\alpha _Q=h_Q^{-1}\alpha $
.
Step 3: We show that
![]() $\gamma $
is a homomorphism of partial groups and thus the assertion holds by Step 2. For the proof let
$\gamma $
is a homomorphism of partial groups and thus the assertion holds by Step 2. For the proof let
![]() $w=(f_1,\dots ,f_n)\in \mathbf {D}^+$
. If
$w=(f_1,\dots ,f_n)\in \mathbf {D}^+$
. If
![]() $w\in \mathbf {D}$
, then
$w\in \mathbf {D}$
, then
![]() $\Pi ^+(w)\gamma =\Pi (w)\alpha =\widetilde {\Pi }(w\alpha ^*)=\widetilde {\Pi }(w\gamma ^*)$
because
$\Pi ^+(w)\gamma =\Pi (w)\alpha =\widetilde {\Pi }(w\alpha ^*)=\widetilde {\Pi }(w\gamma ^*)$
because
![]() $\gamma |_{\mathcal L}=\alpha $
is assumed to be a homomorphism of partial groups. Thus, we may assume
$\gamma |_{\mathcal L}=\alpha $
is assumed to be a homomorphism of partial groups. Thus, we may assume
![]() $w\not \in \mathbf {D}$
. Then
$w\not \in \mathbf {D}$
. Then
![]() $w\in \mathbf {D}^+$
via
$w\in \mathbf {D}^+$
via
![]() $P_0^*,P_1^*,\dots ,P_n^*\in \Delta ^+\backslash \Delta $
. Thus, upon setting
$P_0^*,P_1^*,\dots ,P_n^*\in \Delta ^+\backslash \Delta $
. Thus, upon setting
![]() $P_i:=P_i^*\cap T$
for
$P_i:=P_i^*\cap T$
for
![]() $i=0,1,\dots ,n$
, it follows from our assumption that
$i=0,1,\dots ,n$
, it follows from our assumption that
Notice that
![]() $P_0,P_1,\dots ,P_n$
are all
$P_0,P_1,\dots ,P_n$
are all
![]() $\mathcal {F}$
-conjugate and so
$\mathcal {F}$
-conjugate and so
![]() $Q:=Q_{P_0}=Q_{P_i}$
for
$Q:=Q_{P_0}=Q_{P_i}$
for
![]() $i=1,\dots ,n$
. Set
$i=1,\dots ,n$
. Set
![]() $h_i:=h_{P_i}$
for
$h_i:=h_{P_i}$
for
![]() $i=0,1,\dots ,n$
. By Step 1,
$i=0,1,\dots ,n$
. By Step 1,
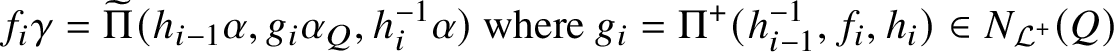 $$ \begin{align} f_i\gamma=\widetilde{\Pi}(h_{i-1}\alpha,g_i\alpha_Q,h_i^{-1}\alpha)\mbox{ where }g_i=\Pi^+(h_{i-1}^{-1},f_i,h_i)\in N_{\mathcal L^+}(Q) \end{align} $$
$$ \begin{align} f_i\gamma=\widetilde{\Pi}(h_{i-1}\alpha,g_i\alpha_Q,h_i^{-1}\alpha)\mbox{ where }g_i=\Pi^+(h_{i-1}^{-1},f_i,h_i)\in N_{\mathcal L^+}(Q) \end{align} $$
for
![]() $i=1,\dots ,n$
. Set
$i=1,\dots ,n$
. Set
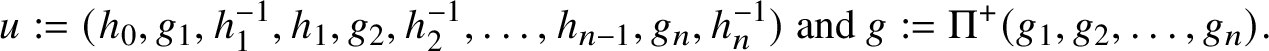 $$ \begin{align*}u:=(h_0,g_1,h_1^{-1},h_1,g_2,h_2^{-1},\dots,h_{n-1},g_n,h_n^{-1})\mbox{ and }g:=\Pi^+(g_1,g_2,\dots,g_n).\end{align*} $$
$$ \begin{align*}u:=(h_0,g_1,h_1^{-1},h_1,g_2,h_2^{-1},\dots,h_{n-1},g_n,h_n^{-1})\mbox{ and }g:=\Pi^+(g_1,g_2,\dots,g_n).\end{align*} $$
Using Step 2, we see that
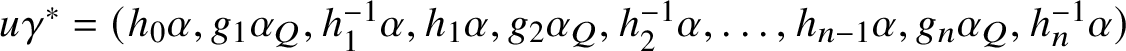 $u\gamma ^*=(h_0\alpha ,g_1\alpha _Q,h_1^{-1}\alpha ,h_1\alpha ,g_2\alpha _Q,h_2^{-1}\alpha ,\dots ,h_{n-1}\alpha ,g_n\alpha _Q,h_n^{-1}\alpha )$
. Notice that
$u\gamma ^*=(h_0\alpha ,g_1\alpha _Q,h_1^{-1}\alpha ,h_1\alpha ,g_2\alpha _Q,h_2^{-1}\alpha ,\dots ,h_{n-1}\alpha ,g_n\alpha _Q,h_n^{-1}\alpha )$
. Notice that
![]() $u\in \mathbf {D}^+$
via
$u\in \mathbf {D}^+$
via
![]() $P_0,Q,Q,P_1,\dots ,P_{n-1},Q,Q,P_n$
. Similarly, because
$P_0,Q,Q,P_1,\dots ,P_{n-1},Q,Q,P_n$
. Similarly, because
![]() $\alpha $
is a homomorphism of partial groups and
$\alpha $
is a homomorphism of partial groups and
![]() $g_i\alpha _Q\in N_{\widetilde {\mathcal {L}}}(Q\alpha )$
for
$g_i\alpha _Q\in N_{\widetilde {\mathcal {L}}}(Q\alpha )$
for
![]() $i=1,\dots ,n$
, we have
$i=1,\dots ,n$
, we have
![]() $u\gamma ^*\in \widetilde {\mathbf {D}}$
via
$u\gamma ^*\in \widetilde {\mathbf {D}}$
via
![]() $P_0\alpha ,Q\alpha ,Q\alpha ,P_1\alpha ,\dots ,P_{n-1}\alpha ,Q\alpha ,Q\alpha ,P_n\alpha $
. Using (3.1.2) and applying axiom (PG3) of a partial group and Lemma 2.2(b) several times, we get that
$P_0\alpha ,Q\alpha ,Q\alpha ,P_1\alpha ,\dots ,P_{n-1}\alpha ,Q\alpha ,Q\alpha ,P_n\alpha $
. Using (3.1.2) and applying axiom (PG3) of a partial group and Lemma 2.2(b) several times, we get that
![]() $w\gamma ^*=(f_1\gamma ,\dots ,f_n\gamma )\in \widetilde {\mathbf {D}}$
and
$w\gamma ^*=(f_1\gamma ,\dots ,f_n\gamma )\in \widetilde {\mathbf {D}}$
and
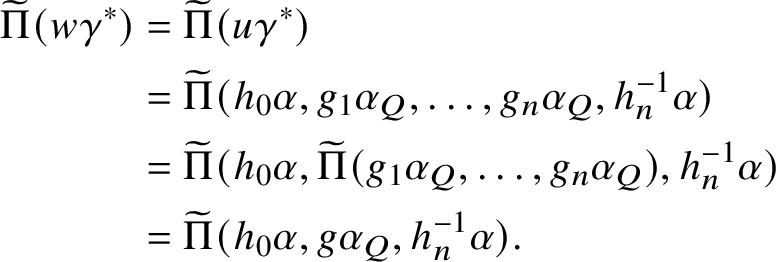 $$ \begin{align*} \widetilde{\Pi}(w\gamma^*)&=\widetilde{\Pi}(u\gamma^*)\\ &=\widetilde{\Pi}(h_0\alpha,g_1\alpha_Q,\dots,g_n\alpha_Q,h_n^{-1}\alpha)\\ &=\widetilde{\Pi}(h_0\alpha,\widetilde{\Pi}(g_1\alpha_Q,\dots,g_n\alpha_Q),h_n^{-1}\alpha)\\ &=\widetilde{\Pi}(h_0\alpha,g\alpha_Q,h_n^{-1}\alpha). \end{align*} $$
$$ \begin{align*} \widetilde{\Pi}(w\gamma^*)&=\widetilde{\Pi}(u\gamma^*)\\ &=\widetilde{\Pi}(h_0\alpha,g_1\alpha_Q,\dots,g_n\alpha_Q,h_n^{-1}\alpha)\\ &=\widetilde{\Pi}(h_0\alpha,\widetilde{\Pi}(g_1\alpha_Q,\dots,g_n\alpha_Q),h_n^{-1}\alpha)\\ &=\widetilde{\Pi}(h_0\alpha,g\alpha_Q,h_n^{-1}\alpha). \end{align*} $$
Observe also that
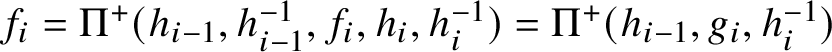 $f_i=\Pi ^+(h_{i-1},h_{i-1}^{-1},f_i,h_i,h_i^{-1})=\Pi ^+(h_{i-1},g_i,h_i^{-1})$
for
$f_i=\Pi ^+(h_{i-1},h_{i-1}^{-1},f_i,h_i,h_i^{-1})=\Pi ^+(h_{i-1},g_i,h_i^{-1})$
for
![]() $i=1,\dots ,n$
. So, similarly, again using axiom (PG3) and Lemma 2.2(b) repeatedly, we see that
$i=1,\dots ,n$
. So, similarly, again using axiom (PG3) and Lemma 2.2(b) repeatedly, we see that
 $$ \begin{align*}f:=\Pi^+(w)=\Pi^+(u)=\Pi^+(h_0,g_1,\dots,g_n,h_n^{-1})=\Pi^+(h_0,g,h_n^{-1})\in N_{\mathcal L^+}(P_0,P_n).\end{align*} $$
$$ \begin{align*}f:=\Pi^+(w)=\Pi^+(u)=\Pi^+(h_0,g_1,\dots,g_n,h_n^{-1})=\Pi^+(h_0,g,h_n^{-1})\in N_{\mathcal L^+}(P_0,P_n).\end{align*} $$
Because
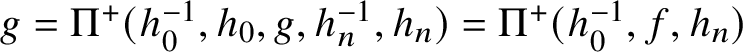 $g=\Pi ^+(h_0^{-1},h_0,g,h_n^{-1},h_n)=\Pi ^+(h_0^{-1},f,h_n)$
, it follows from Step 1 that
$g=\Pi ^+(h_0^{-1},h_0,g,h_n^{-1},h_n)=\Pi ^+(h_0^{-1},f,h_n)$
, it follows from Step 1 that
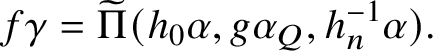 $$ \begin{align*}f\gamma=\widetilde{\Pi}(h_0\alpha,g\alpha_Q,h_n^{-1}\alpha).\end{align*} $$
$$ \begin{align*}f\gamma=\widetilde{\Pi}(h_0\alpha,g\alpha_Q,h_n^{-1}\alpha).\end{align*} $$
Putting everything together, we get
![]() $\Pi ^+(w)\gamma =f\gamma =\widetilde {\Pi }(w\gamma ^*)$
and thus
$\Pi ^+(w)\gamma =f\gamma =\widetilde {\Pi }(w\gamma ^*)$
and thus
![]() $\gamma $
is a homomorphism of partial groups. This completes Step 3 and the proof of the assertion.
$\gamma $
is a homomorphism of partial groups. This completes Step 3 and the proof of the assertion.
Corollary 3.2. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
and
$(\mathcal L^+,\Delta ^+,S)$
and
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
be localities, and let
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
be localities, and let
![]() $\Delta $
be a nonempty subset of
$\Delta $
be a nonempty subset of
![]() $\Delta ^+$
that is
$\Delta ^+$
that is
![]() $\mathcal {F}_S(\mathcal L^+)$
-closed. Set
$\mathcal {F}_S(\mathcal L^+)$
-closed. Set
![]() $\mathcal L:=\mathcal L^+|_\Delta $
. Assume that every proper overgroup in S of an element of
$\mathcal L:=\mathcal L^+|_\Delta $
. Assume that every proper overgroup in S of an element of
![]() $\Delta ^+\backslash \Delta $
is in
$\Delta ^+\backslash \Delta $
is in
![]() $\Delta $
. Suppose we are given
$\Delta $
. Suppose we are given
-
• a homomorphism of partial groups
 $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
 $\Delta ^+\alpha \subseteq \widetilde {\Delta }$
;
$\Delta ^+\alpha \subseteq \widetilde {\Delta }$
; -
• a set
 $\Gamma _0\subseteq \Delta ^+\backslash \Delta $
of fully
$\Gamma _0\subseteq \Delta ^+\backslash \Delta $
of fully
 $\mathcal {F}_S(\mathcal L^+)$
-normalised representatives of the
$\mathcal {F}_S(\mathcal L^+)$
-normalised representatives of the
 $\mathcal {F}_S(\mathcal L^+)$
-conjugacy classes of the subgroups in
$\mathcal {F}_S(\mathcal L^+)$
-conjugacy classes of the subgroups in
 $\Delta ^+\backslash \Delta $
; and
$\Delta ^+\backslash \Delta $
; and -
• for each
 $Q\in \Gamma _0$
a homomorphism of groups
$Q\in \Gamma _0$
a homomorphism of groups
 $\alpha _Q\colon N_{\mathcal L^+}(Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
with
$\alpha _Q\colon N_{\mathcal L^+}(Q)\longrightarrow N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
with
 $\alpha _Q|_{N_{\mathcal L}(Q)}=\alpha |_{N_{\mathcal L}(Q)}$
.
$\alpha _Q|_{N_{\mathcal L}(Q)}=\alpha |_{N_{\mathcal L}(Q)}$
.
Then there exists a unique homomorphism of partial groups
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\gamma |_{\mathcal L}=\alpha $
and
$\gamma |_{\mathcal L}=\alpha $
and
![]() $\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
$\gamma |_{N_{\mathcal L^+}(Q)}=\alpha _Q$
for every
![]() $Q\in \Gamma _0$
.
$Q\in \Gamma _0$
.
Proof. Apply Lemma 3.1 with S in place of T.
In the proofs of our main theorems, Lemma 3.1 will be used in the form of the following corollary.
Corollary 3.3. Let
![]() $(\mathcal L^+,\Delta ^+,S)$
and
$(\mathcal L^+,\Delta ^+,S)$
and
![]() $(\mathcal L,\Delta ,S)$
be linking localities over the same fusion system
$(\mathcal L,\Delta ,S)$
be linking localities over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
. Suppose we are given a locality
$\mathcal L=\mathcal L^+|_\Delta $
. Suppose we are given a locality
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
and a homomorphism of partial groups
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
and a homomorphism of partial groups
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\Delta ^+\alpha \subseteq \widetilde {\Delta }$
. Then there exists a unique homomorphism of partial groups
$\Delta ^+\alpha \subseteq \widetilde {\Delta }$
. Then there exists a unique homomorphism of partial groups
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\gamma |_{\mathcal L}=\alpha $
.
$\gamma |_{\mathcal L}=\alpha $
.
Proof. We first prove the assertion under the following additional hypothesis:
Notice that
![]() $\Delta ^+\backslash \Delta $
is closed under
$\Delta ^+\backslash \Delta $
is closed under
![]() $\mathcal {F}$
-conjugacy, because
$\mathcal {F}$
-conjugacy, because
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^+$
are closed under
$\Delta ^+$
are closed under
![]() $\mathcal {F}$
-conjugacy. Thus, we may choose a set
$\mathcal {F}$
-conjugacy. Thus, we may choose a set
![]() $\Gamma _0\subseteq \Delta ^+\backslash \Delta $
of fully
$\Gamma _0\subseteq \Delta ^+\backslash \Delta $
of fully
![]() $\mathcal {F}$
-normalised representatives of the
$\mathcal {F}$
-normalised representatives of the
![]() $\mathcal {F}$
-conjugacy classes of the elements in
$\mathcal {F}$
-conjugacy classes of the elements in
![]() $\Delta ^+\backslash \Delta $
. By Lemma 2.26, for every
$\Delta ^+\backslash \Delta $
. By Lemma 2.26, for every
![]() $Q\in \Gamma _0$
, the normaliser
$Q\in \Gamma _0$
, the normaliser
![]() $N_{\mathcal L}(Q)=N_{\mathcal L^+}(Q)$
is a subgroup of
$N_{\mathcal L}(Q)=N_{\mathcal L^+}(Q)$
is a subgroup of
![]() $\mathcal L$
. Because
$\mathcal L$
. Because
![]() $\alpha $
is a homomorphism of partial groups, we have
$\alpha $
is a homomorphism of partial groups, we have
![]() $N_{\mathcal L}(Q)\alpha \subseteq N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Because we assume that
$N_{\mathcal L}(Q)\alpha \subseteq N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Because we assume that
![]() $Q\alpha \in \Delta ^+\alpha \subseteq \widetilde {\Delta }$
, the normaliser
$Q\alpha \in \Delta ^+\alpha \subseteq \widetilde {\Delta }$
, the normaliser
![]() $N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
is a subgroup of
$N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
is a subgroup of
![]() ${\widetilde {\mathcal {L}}}$
. So
${\widetilde {\mathcal {L}}}$
. So
![]() $\alpha _Q:=\alpha |_{N_{\mathcal L}(Q)}$
is a homomorphism of groups from
$\alpha _Q:=\alpha |_{N_{\mathcal L}(Q)}$
is a homomorphism of groups from
![]() $N_{\mathcal L}(Q)=N_{\mathcal L^+}(Q)$
to
$N_{\mathcal L}(Q)=N_{\mathcal L^+}(Q)$
to
![]() $N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Now the assertion follows from Corollary 3.2.
$N_{{\widetilde {\mathcal {L}}}}(Q\alpha )$
. Now the assertion follows from Corollary 3.2.
We now remove the extra hypothesis (*). Let
![]() $\Gamma $
be the set of the elements in
$\Gamma $
be the set of the elements in
![]() $\Delta ^+\backslash \Delta $
of maximal order. Then
$\Delta ^+\backslash \Delta $
of maximal order. Then
![]() $\Gamma $
is closed under
$\Gamma $
is closed under
![]() $\mathcal {F}$
-conjugacy, because
$\mathcal {F}$
-conjugacy, because
![]() $\Delta ^+\backslash \Delta $
is closed under
$\Delta ^+\backslash \Delta $
is closed under
![]() $\mathcal {F}$
-conjugacy. Moreover, because
$\mathcal {F}$
-conjugacy. Moreover, because
![]() $\Delta ^+$
is overgroup closed in S, every proper overgroup of an element of
$\Delta ^+$
is overgroup closed in S, every proper overgroup of an element of
![]() $\Gamma $
is in
$\Gamma $
is in
![]() $\Delta $
. In particular, because
$\Delta $
. In particular, because
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {F}$
-closed, the set
$\mathcal {F}$
-closed, the set
![]() $\Delta ^*:=\Delta \cup \Gamma $
is
$\Delta ^*:=\Delta \cup \Gamma $
is
![]() $\mathcal {F}$
-closed and
$\mathcal {F}$
-closed and
![]() $\mathcal L^*:=\mathcal L^+|_{\Delta }$
is well defined. Then
$\mathcal L^*:=\mathcal L^+|_{\Delta }$
is well defined. Then
![]() $(\mathcal L^*,\Delta ^*,S)$
is a locality with
$(\mathcal L^*,\Delta ^*,S)$
is a locality with
![]() $\mathcal {F}^{cr}\subseteq \Delta \subseteq \Delta ^*$
and
$\mathcal {F}^{cr}\subseteq \Delta \subseteq \Delta ^*$
and
![]() $\mathcal L^*|_\Delta =\mathcal L$
. Moreover,
$\mathcal L^*|_\Delta =\mathcal L$
. Moreover,
![]() $N_{\mathcal L^*}(P)=N_{\mathcal L^+}(P)$
is of characteristic p for every
$N_{\mathcal L^*}(P)=N_{\mathcal L^+}(P)$
is of characteristic p for every
![]() $P\in \Delta ^*$
. Hence, using Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver1, Theorem I.3.6], we conclude that
$P\in \Delta ^*$
. Hence, using Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver1, Theorem I.3.6], we conclude that
![]() $(\mathcal L^*,\Delta ^*,S)$
is a linking locality over
$(\mathcal L^*,\Delta ^*,S)$
is a linking locality over
![]() $\mathcal {F}$
. Notice that (*) is fulfilled with
$\mathcal {F}$
. Notice that (*) is fulfilled with
![]() $\Delta ^*$
in place of
$\Delta ^*$
in place of
![]() $\Delta ^+$
. As we proved at the beginning, there thus exists a unique homomorphism of partial groups
$\Delta ^+$
. As we proved at the beginning, there thus exists a unique homomorphism of partial groups
![]() $\gamma ^*\colon \mathcal L^*\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\gamma ^*\colon \mathcal L^*\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\gamma ^*|_{\mathcal L}=\alpha $
. Now by induction on
$\gamma ^*|_{\mathcal L}=\alpha $
. Now by induction on
![]() $|\Delta ^+\backslash \Delta |$
, there exists a unique homomorphism of partial groups
$|\Delta ^+\backslash \Delta |$
, there exists a unique homomorphism of partial groups
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\gamma |_{\mathcal L^*}=\gamma ^*$
. Then
$\gamma |_{\mathcal L^*}=\gamma ^*$
. Then
![]() $\gamma |_{\mathcal L}=\gamma ^*|_{\mathcal L}=\alpha $
. Moreover, if
$\gamma |_{\mathcal L}=\gamma ^*|_{\mathcal L}=\alpha $
. Moreover, if
![]() $\beta \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
$\beta \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
with
![]() $\beta |_{\mathcal L}=\alpha $
, then
$\beta |_{\mathcal L}=\alpha $
, then
![]() $\beta ^*:=\beta |_{\mathcal L^*}$
is a homomorphism of partial groups from
$\beta ^*:=\beta |_{\mathcal L^*}$
is a homomorphism of partial groups from
![]() $\mathcal L^*$
to
$\mathcal L^*$
to
![]() ${\widetilde {\mathcal {L}}}$
with
${\widetilde {\mathcal {L}}}$
with
![]() $\beta ^*|_{\mathcal L}=\alpha $
. Because
$\beta ^*|_{\mathcal L}=\alpha $
. Because
![]() $\gamma ^*$
is unique, it follows that
$\gamma ^*$
is unique, it follows that
![]() $\beta |_{\mathcal L^*}=\beta ^*=\gamma ^*$
, and then the unique choice of
$\beta |_{\mathcal L^*}=\beta ^*=\gamma ^*$
, and then the unique choice of
![]() $\gamma $
implies
$\gamma $
implies
![]() $\beta =\gamma $
. This proves the assertion.
$\beta =\gamma $
. This proves the assertion.
4. Transporter systems
Transporter systems are certain categories associated to fusion systems that were introduced by Oliver and Ventura Reference Oliver and Ventura[21]. As shown by Chermak [Reference Chermak6, Appendix A], there is a one-to-one correspondence between localities and transporter systems, which we will outline in Subsection 4.2. Moreover, we will introduce isomorphisms between transporter systems in Subsection 4.1 and linking systems in Subsection 4.3.
Because the literature on transporter systems is mainly written in ‘left-hand notation’, in this section we will write functions on the left side of the argument. Similarly, we will conjugate from the left. Given a group G, we set
![]() ${}^g\!x:=gxg^{-1}$
and
${}^g\!x:=gxg^{-1}$
and
![]() ${}^g\!P=gPg^{-1}$
for all
${}^g\!P=gPg^{-1}$
for all
![]() $x,g\in G$
and
$x,g\in G$
and
![]() $P\subseteq G$
. So conjugation by g from the left corresponds to conjugation by
$P\subseteq G$
. So conjugation by g from the left corresponds to conjugation by
![]() $g^{-1}$
from the right.
$g^{-1}$
from the right.
4.1. Isomorphisms between transporter systems
If
![]() $\Delta $
is a set of subgroups of G, write
$\Delta $
is a set of subgroups of G, write
![]() $\mathcal {T}_\Delta (G)$
for the category whose object set is
$\mathcal {T}_\Delta (G)$
for the category whose object set is
![]() $\Delta $
and whose morphism set between two subgroups
$\Delta $
and whose morphism set between two subgroups
![]() $P,Q\in \Delta $
is
$P,Q\in \Delta $
is
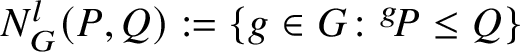 $N_G^l(P,Q):=\{g\in G\colon {}^g\!P\leq Q\}$
or, more precisely, the set of triples
$N_G^l(P,Q):=\{g\in G\colon {}^g\!P\leq Q\}$
or, more precisely, the set of triples
![]() $(P,Q,g)$
with
$(P,Q,g)$
with
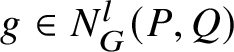 $g\in N_G^l(P,Q)$
. Here composition of morphisms corresponds to the group multiplication.
$g\in N_G^l(P,Q)$
. Here composition of morphisms corresponds to the group multiplication.
A transporter system associated to a fusion system
![]() $\mathcal {F}$
over S is a category
$\mathcal {F}$
over S is a category
![]() $\mathcal {T}$
whose set
$\mathcal {T}$
whose set
![]() $\Delta $
of objects is an
$\Delta $
of objects is an
![]() $\mathcal {F}$
-closed collection of subgroups of S, together with functors
$\mathcal {F}$
-closed collection of subgroups of S, together with functors
 $$ \begin{align*}\mathcal{T}_\Delta(S)\xrightarrow{\;\;\;\delta\;\;\;}\mathcal{T}\xrightarrow{\;\;\;\pi\;\;\;}\mathcal{F}\end{align*} $$
$$ \begin{align*}\mathcal{T}_\Delta(S)\xrightarrow{\;\;\;\delta\;\;\;}\mathcal{T}\xrightarrow{\;\;\;\pi\;\;\;}\mathcal{F}\end{align*} $$
subject to certain axioms. For example,
![]() $\delta $
is the identity on objects and injective on morphism sets, and
$\delta $
is the identity on objects and injective on morphism sets, and
![]() $\pi $
is the inclusion on objects and surjective on morphism sets; see [Reference Oliver and Ventura21, Definition 3.1] for details. If we want to be more precise, we say that
$\pi $
is the inclusion on objects and surjective on morphism sets; see [Reference Oliver and Ventura21, Definition 3.1] for details. If we want to be more precise, we say that
![]() $(\mathcal {T},\delta ,\pi )$
is a transporter system. By [Reference Oliver and Ventura21, Lemma A.6], if
$(\mathcal {T},\delta ,\pi )$
is a transporter system. By [Reference Oliver and Ventura21, Lemma A.6], if
![]() $P\in \Delta $
, then every element of
$P\in \Delta $
, then every element of
![]() $\mathrm {Aut}_{\mathcal {T}}(P):=\mathrm {Mor}_{\mathcal {T}}(P,P)$
is an isomorphism and so
$\mathrm {Aut}_{\mathcal {T}}(P):=\mathrm {Mor}_{\mathcal {T}}(P,P)$
is an isomorphism and so
![]() $\mathrm {Aut}_{\mathcal {T}}(P)$
is a group. We set
$\mathrm {Aut}_{\mathcal {T}}(P)$
is a group. We set
![]() $\delta _P:=\delta _{P,P}$
and
$\delta _P:=\delta _{P,P}$
and
![]() $\pi _P:=\pi _{P,P}$
for every
$\pi _P:=\pi _{P,P}$
for every
![]() $P\in \Delta $
. Similarly, we set
$P\in \Delta $
. Similarly, we set
![]() $\alpha _P:=\alpha _{P,P}$
for every functor
$\alpha _P:=\alpha _{P,P}$
for every functor
![]() $\alpha $
from
$\alpha $
from
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
If
![]() $\mathcal {T}$
is a transporter system and
$\mathcal {T}$
is a transporter system and
![]() $P,Q\in \mathrm {Ob}(\mathcal {T}\;)$
, then
$P,Q\in \mathrm {Ob}(\mathcal {T}\;)$
, then
![]() $\delta _{P,Q}(1)$
should be thought of as the inclusion map. Given
$\delta _{P,Q}(1)$
should be thought of as the inclusion map. Given
![]() $P,Q,P_0,Q_0\in \mathrm {Ob}(\mathcal {T}\;)$
and
$P,Q,P_0,Q_0\in \mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\psi \in \mathrm {Mor}_{\mathcal {T}}(P,Q)$
with
$\psi \in \mathrm {Mor}_{\mathcal {T}}(P,Q)$
with
![]() $P_0\leq P$
,
$P_0\leq P$
,
![]() $Q_0\leq Q$
and
$Q_0\leq Q$
and
![]() $\pi (\psi )(P_0)\leq Q_0$
, by [Reference Oliver and Ventura21, Lemma 3.2(c)], there is a unique morphism
$\pi (\psi )(P_0)\leq Q_0$
, by [Reference Oliver and Ventura21, Lemma 3.2(c)], there is a unique morphism
![]() $\psi _0\in \mathrm {Mor}_{\mathcal {T}}(P_0,Q_0)$
such that
$\psi _0\in \mathrm {Mor}_{\mathcal {T}}(P_0,Q_0)$
such that
![]() $\delta _{Q_0,Q}(1)\circ \psi _0=\psi \circ \delta _{P_0,P}(1)$
. The morphism
$\delta _{Q_0,Q}(1)\circ \psi _0=\psi \circ \delta _{P_0,P}(1)$
. The morphism
![]() $\psi _0$
is then denoted by
$\psi _0$
is then denoted by
![]() $\psi |_{P_0,Q_0}$
and called a restriction of
$\psi |_{P_0,Q_0}$
and called a restriction of
![]() $\psi $
. On the other hand, if
$\psi $
. On the other hand, if
![]() $\psi _0$
is given, then because every morphism in
$\psi _0$
is given, then because every morphism in
![]() $\mathcal {T}$
is an epimorphism by [Reference Oliver and Ventura21, Lemma 3.2(d)], the ‘extension’
$\mathcal {T}$
is an epimorphism by [Reference Oliver and Ventura21, Lemma 3.2(d)], the ‘extension’
![]() $\psi $
is uniquely determined if it exists.
$\psi $
is uniquely determined if it exists.
Definition 4.1. Let
![]() $(\mathcal {T},\delta ,\pi )$
and
$(\mathcal {T},\delta ,\pi )$
and
![]() $({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
be transporter systems associated to fusion systems
$({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
be transporter systems associated to fusion systems
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() ${\widetilde {\mathcal {F}}}$
over p-groups S and
${\widetilde {\mathcal {F}}}$
over p-groups S and
![]() ${\widetilde {S}}$
, respectively.
${\widetilde {S}}$
, respectively.
-
• An equivalence of categories
 $\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
is called an isomorphism if
$\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
is called an isomorphism if-
–
 $\alpha $
is isotypical; that is,
$\alpha $
is isotypical; that is,
 $\alpha _P(\delta _P(P))={\tilde {\delta }}_{\alpha (P)}(\alpha (P))$
for every
$\alpha _P(\delta _P(P))={\tilde {\delta }}_{\alpha (P)}(\alpha (P))$
for every
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
; and
$P\in \mathrm {Ob}(\mathcal {T}\;)$
; and -
–
 $\alpha $
sends inclusions to inclusions; that is,
$\alpha $
sends inclusions to inclusions; that is,
 $\alpha _{P,Q}(\delta _{P,Q}(1))={\tilde {\delta }}_{\alpha (P),\alpha (Q)}(1)$
for all
$\alpha _{P,Q}(\delta _{P,Q}(1))={\tilde {\delta }}_{\alpha (P),\alpha (Q)}(1)$
for all
 $P,Q\in \mathrm {Ob}(\mathcal {T}\;)$
.
$P,Q\in \mathrm {Ob}(\mathcal {T}\;)$
.
We write
 $\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
for the set of isomorphisms from
$\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
for the set of isomorphisms from
 $\mathcal {T}$
to
$\mathcal {T}$
to
 ${\widetilde {\mathcal {T}}}$
.
${\widetilde {\mathcal {T}}}$
. -
-
• If
 $\Gamma $
and
$\Gamma $
and
 $\widetilde {\Gamma }$
are sets of subgroups of S and
$\widetilde {\Gamma }$
are sets of subgroups of S and
 ${\widetilde {S}}$
, respectively, then we write
${\widetilde {S}}$
, respectively, then we write
 $\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
for the set of isomorphisms
$\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
for the set of isomorphisms
 $\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
with
$\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
with
 $\{\alpha _S(\delta _S(P))\colon P\in \Gamma \}=\{\delta _{\widetilde {S}}(Q)\colon Q\in \widetilde {\Gamma }\}$
.
$\{\alpha _S(\delta _S(P))\colon P\in \Gamma \}=\{\delta _{\widetilde {S}}(Q)\colon Q\in \widetilde {\Gamma }\}$
. -
• An isomorphism
 $\alpha \colon \mathcal {T}\rightarrow {\widetilde {\mathcal {T}}}$
is called rigid if
$\alpha \colon \mathcal {T}\rightarrow {\widetilde {\mathcal {T}}}$
is called rigid if
 $S={\widetilde {S}}$
and
$S={\widetilde {S}}$
and
 $\alpha _S\circ \delta _S={\tilde {\delta }}_{\widetilde {S}}$
.
$\alpha _S\circ \delta _S={\tilde {\delta }}_{\widetilde {S}}$
. -
• An automorphism of
 $\mathcal {T}$
is an isomorphism
$\mathcal {T}$
is an isomorphism
 $\mathcal {T}\longrightarrow \mathcal {T}$
. Set
$\mathcal {T}\longrightarrow \mathcal {T}$
. Set
 $\mathrm {Aut}(\mathcal {T}\;):=\mathrm {Iso}(\mathcal {T},\mathcal {T})$
and, for any set
$\mathrm {Aut}(\mathcal {T}\;):=\mathrm {Iso}(\mathcal {T},\mathcal {T})$
and, for any set
 $\Gamma $
of subgroups of S, set
$\Gamma $
of subgroups of S, set
 $\mathrm {Aut}(\mathcal {T}\;)_\Gamma :=\mathrm {Iso}(\mathcal {T},\mathcal {T})_{\Gamma ,\Gamma }$
.
$\mathrm {Aut}(\mathcal {T}\;)_\Gamma :=\mathrm {Iso}(\mathcal {T},\mathcal {T})_{\Gamma ,\Gamma }$
. -
• If
 $\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
, then an automorphism
$\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
, then an automorphism
 $c_\gamma \in \mathrm {Aut}(\mathcal {T}\;)$
is defined on objects via
$c_\gamma \in \mathrm {Aut}(\mathcal {T}\;)$
is defined on objects via
 $P\mapsto c_\gamma (P):=\pi (\gamma )(P)$
and on morphisms
$P\mapsto c_\gamma (P):=\pi (\gamma )(P)$
and on morphisms
 $\varphi \in \mathrm {Hom}_{\mathcal {T}}(P,Q)$
by sending
$\varphi \in \mathrm {Hom}_{\mathcal {T}}(P,Q)$
by sending
 $\varphi $
to We will refer to
$\varphi $
to We will refer to $$ \begin{align*}c_\gamma(\varphi):=\gamma|_{Q,c_\gamma(Q)} \circ \varphi \circ (\gamma|_{P,c_\gamma(P)})^{-1}\in\mathrm{Hom}_{\mathcal{T}}(c_\gamma(P),c_\gamma(Q)).\end{align*} $$
$$ \begin{align*}c_\gamma(\varphi):=\gamma|_{Q,c_\gamma(Q)} \circ \varphi \circ (\gamma|_{P,c_\gamma(P)})^{-1}\in\mathrm{Hom}_{\mathcal{T}}(c_\gamma(P),c_\gamma(Q)).\end{align*} $$
 $c_\gamma $
as the automorphism of
$c_\gamma $
as the automorphism of
 $\mathcal {T}$
induced by conjugation by
$\mathcal {T}$
induced by conjugation by
 $\gamma $
. The group of automorphisms of
$\gamma $
. The group of automorphisms of
 $\mathcal {T}$
of the form
$\mathcal {T}$
of the form
 $c_\gamma $
with
$c_\gamma $
with
 $\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
is called the group of inner automorphisms of
$\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
is called the group of inner automorphisms of
 $\mathcal {T}$
.
$\mathcal {T}$
.
-
• Let
 $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
be the set of natural isomorphism classes of isotypical self-equivalences of
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
be the set of natural isomorphism classes of isotypical self-equivalences of
 $\mathcal L$
.
$\mathcal L$
.
It should be noted that
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is a submonoid of the (finite) group of natural isomorphism classes of self-equivalences of
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is a submonoid of the (finite) group of natural isomorphism classes of self-equivalences of
![]() $\mathcal L$
and thus forms a finite group. In Lemma 4.10 we will see that
$\mathcal L$
and thus forms a finite group. In Lemma 4.10 we will see that
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is actually the image of
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is actually the image of
![]() $\mathrm {Aut}(\mathcal {T}\;)$
under a homomorphism whose kernel is the group of inner automorphisms.
$\mathrm {Aut}(\mathcal {T}\;)$
under a homomorphism whose kernel is the group of inner automorphisms.
The above definition of isomorphisms and rigid isomorphisms of transporter systems follows Glauberman–Lynd [Reference Glauberman and Lynd12, Definition 2.3]. The definition of isomorphisms used previously in the literature (e.g., in [Reference Broto, Levi and Oliver3, p.799], [Reference Aschbacher, Kessar and Oliver1, p.146] and [Reference Chermak6, Definition A.2]) is different. In the situations we care about (in particular, when we consider linking systems later on), it agrees with the definition of a rigid isomorphism as we explain in Remark 4.2(d). The group
![]() $\mathrm {Aut}(\mathcal {T}\;)$
is also often denoted by
$\mathrm {Aut}(\mathcal {T}\;)$
is also often denoted by
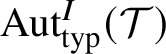 $\mathrm {Aut}_{\operatorname {typ}}^I(\mathcal {T}\;)$
; see, for example, [Reference Aschbacher, Kessar and Oliver1, p.153].
$\mathrm {Aut}_{\operatorname {typ}}^I(\mathcal {T}\;)$
; see, for example, [Reference Aschbacher, Kessar and Oliver1, p.153].
Remark 4.2. Suppose that
![]() $(\mathcal {T},\delta ,S)$
and
$(\mathcal {T},\delta ,S)$
and
![]() $({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
are transporter systems over fusion systems
$({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
are transporter systems over fusion systems
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() ${\widetilde {\mathcal {F}}}$
, respectively, and let
${\widetilde {\mathcal {F}}}$
, respectively, and let
![]() $\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
be an isomorphism of transporter systems.
$\alpha \colon \mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
be an isomorphism of transporter systems.
-
(a) It follows from the axioms of a transporter system that
 $\delta _S\colon S\longrightarrow \mathrm {Aut}_{\mathcal {T}}(S)$
is a group homomorphism whose image
$\delta _S\colon S\longrightarrow \mathrm {Aut}_{\mathcal {T}}(S)$
is a group homomorphism whose image
 $\delta _S(S)$
is a normal Sylow p-subgroup of
$\delta _S(S)$
is a normal Sylow p-subgroup of
 $\mathrm {Aut}_{\mathcal {T}}(S)$
. Similarly,
$\mathrm {Aut}_{\mathcal {T}}(S)$
. Similarly,
 ${\tilde {\delta }}_{\widetilde {S}}({\widetilde {S}})$
is a normal Sylow p-subgroup of
${\tilde {\delta }}_{\widetilde {S}}({\widetilde {S}})$
is a normal Sylow p-subgroup of
 $\mathrm {Aut}_{\widetilde {\mathcal {T}}}({\widetilde {S}})$
. In particular, is an isomorphism of groups that takes
$\mathrm {Aut}_{\widetilde {\mathcal {T}}}({\widetilde {S}})$
. In particular, is an isomorphism of groups that takes $$ \begin{align*}\alpha_S\colon \mathrm{Aut}_{\mathcal{T}}\;(S)\longrightarrow\mathrm{Aut}_{\widetilde{\mathcal{T}}}({\widetilde{S}})\end{align*} $$
$$ \begin{align*}\alpha_S\colon \mathrm{Aut}_{\mathcal{T}}\;(S)\longrightarrow\mathrm{Aut}_{\widetilde{\mathcal{T}}}({\widetilde{S}})\end{align*} $$
 $\delta _S(S)$
to
$\delta _S(S)$
to
 ${\tilde {\delta }}_{\widetilde {S}}({\widetilde {S}})$
. So writing
${\tilde {\delta }}_{\widetilde {S}}({\widetilde {S}})$
. So writing
 ${\tilde {\delta }}_{\widetilde {S}}^{-1}$
for the inverse of the map
${\tilde {\delta }}_{\widetilde {S}}^{-1}$
for the inverse of the map
 ${\widetilde {S}}\rightarrow {\tilde {\delta }}({\widetilde {S}})$
induced by
${\widetilde {S}}\rightarrow {\tilde {\delta }}({\widetilde {S}})$
induced by
 ${\tilde {\delta }}_{\widetilde {S}}$
, the map
${\tilde {\delta }}_{\widetilde {S}}$
, the map
 $\beta :={\tilde {\delta }}_{\widetilde {S}}^{-1}\circ \alpha _S\circ \delta _S$
is a group isomorphism from S to
$\beta :={\tilde {\delta }}_{\widetilde {S}}^{-1}\circ \alpha _S\circ \delta _S$
is a group isomorphism from S to
 ${\widetilde {S}}$
. If
${\widetilde {S}}$
. If
 $\Gamma $
and
$\Gamma $
and
 $\widetilde {\Gamma }$
are sets of subgroups of S and
$\widetilde {\Gamma }$
are sets of subgroups of S and
 ${\widetilde {S}}$
, respectively, notice that
${\widetilde {S}}$
, respectively, notice that
 $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_\Gamma $
if and only if
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_\Gamma $
if and only if
 $\beta (\Gamma ):=\{\beta (P)\colon P\in \Gamma \}$
equals
$\beta (\Gamma ):=\{\beta (P)\colon P\in \Gamma \}$
equals
 $\widetilde {\Gamma }$
.
$\widetilde {\Gamma }$
.
-
(b) As can be seen from the proof of [Reference Glauberman and Lynd12, Proposition 2.5], if
 $\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
$\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
 ${\widetilde {\mathcal {F}}}^{cr}\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
, then the isomorphism
${\widetilde {\mathcal {F}}}^{cr}\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
, then the isomorphism
 $\beta \colon S\rightarrow {\widetilde {S}}$
from (a) induces an isomorphism of fusion systems from
$\beta \colon S\rightarrow {\widetilde {S}}$
from (a) induces an isomorphism of fusion systems from
 $\mathcal {F}$
to
$\mathcal {F}$
to
 ${\widetilde {\mathcal {F}}}$
. In particular, if
${\widetilde {\mathcal {F}}}$
. In particular, if
 $\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
$\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
 $\Gamma $
is an
$\Gamma $
is an
 $\mathrm {Aut}(\mathcal {F})$
-invariant set of subgroups of S, then
$\mathrm {Aut}(\mathcal {F})$
-invariant set of subgroups of S, then
 $\mathrm {Aut}(\mathcal {T}\;)_\Gamma =\mathrm {Aut}(\mathcal {T}\;)$
.
$\mathrm {Aut}(\mathcal {T}\;)_\Gamma =\mathrm {Aut}(\mathcal {T}\;)$
. -
(c) Because
 $\alpha $
maps inclusions to inclusions,
$\alpha $
maps inclusions to inclusions,
 $\alpha $
commutes with taking restrictions and extensions. If
$\alpha $
commutes with taking restrictions and extensions. If
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
, then observe that
$P\in \mathrm {Ob}(\mathcal {T}\;)$
, then observe that
 $\delta _S(x)|_{P,P}=\delta _P(x)$
for every
$\delta _S(x)|_{P,P}=\delta _P(x)$
for every
 $x\in P$
and, similarly,
$x\in P$
and, similarly,
 ${\tilde {\delta }}_{\widetilde {S}}(y)|_{\alpha (P),\alpha (P)}={\tilde {\delta }}_{\alpha (P)}(y)$
for every
${\tilde {\delta }}_{\widetilde {S}}(y)|_{\alpha (P),\alpha (P)}={\tilde {\delta }}_{\alpha (P)}(y)$
for every
 $y\in \alpha (P)$
. Hence, because
$y\in \alpha (P)$
. Hence, because
 $\alpha _P(\delta _P(P))={\tilde {\delta }}_{\alpha (P)}(\alpha (P))$
, it follows that
$\alpha _P(\delta _P(P))={\tilde {\delta }}_{\alpha (P)}(\alpha (P))$
, it follows that
 $\alpha _S(\delta _S(P))={\tilde {\delta }}_{\widetilde {S}}(\alpha (P))$
for every
$\alpha _S(\delta _S(P))={\tilde {\delta }}_{\widetilde {S}}(\alpha (P))$
for every
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
. So if
$P\in \mathrm {Ob}(\mathcal {T}\;)$
. So if
 $\beta \colon S\rightarrow {\widetilde {S}}$
is as in (a), one can see that
$\beta \colon S\rightarrow {\widetilde {S}}$
is as in (a), one can see that
 $\alpha (P)=\beta (P)$
for every
$\alpha (P)=\beta (P)$
for every
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
. Hence,
$P\in \mathrm {Ob}(\mathcal {T}\;)$
. Hence,
 $\alpha $
is a bijection on objects and thus an isomorphism of categories. In particular,
$\alpha $
is a bijection on objects and thus an isomorphism of categories. In particular,
 $\mathrm {Aut}(\mathcal {T}\;)$
is a group. Moreover, if
$\mathrm {Aut}(\mathcal {T}\;)$
is a group. Moreover, if
 $\Gamma \subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
$\Gamma \subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
 $\widetilde {\Gamma }\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
, then
$\widetilde {\Gamma }\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
, then
 $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
if and only if
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
if and only if
 $\{\alpha (P)\colon P\in \Gamma \}=\widetilde {\Gamma }$
.
$\{\alpha (P)\colon P\in \Gamma \}=\widetilde {\Gamma }$
. -
(d) If
 $\alpha $
is a rigid isomorphism, then
$\alpha $
is a rigid isomorphism, then
 $S={\widetilde {S}}$
and the isomorphism
$S={\widetilde {S}}$
and the isomorphism
 $\beta \colon S\rightarrow S$
from (a) is the identity. In particular, by (c), it follows then that
$\beta \colon S\rightarrow S$
from (a) is the identity. In particular, by (c), it follows then that
 $\alpha (P)=P$
for all
$\alpha (P)=P$
for all
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
. If
$P\in \mathrm {Ob}(\mathcal {T}\;)$
. If
 $\mathcal {F}^{cr}\subseteq \mathcal {T}$
and
$\mathcal {F}^{cr}\subseteq \mathcal {T}$
and
 ${\widetilde {\mathcal {F}}}^{cr}\subseteq {\widetilde {\mathcal {T}}}$
, then it is a consequence of [Reference Glauberman and Lynd12, Proposition 2.5] that
${\widetilde {\mathcal {F}}}^{cr}\subseteq {\widetilde {\mathcal {T}}}$
, then it is a consequence of [Reference Glauberman and Lynd12, Proposition 2.5] that
 $\alpha \circ \delta ={\tilde {\delta }}$
and
$\alpha \circ \delta ={\tilde {\delta }}$
and
 ${\tilde {\pi }}\circ \alpha =\pi $
. Thus, in this case a rigid isomorphism
${\tilde {\pi }}\circ \alpha =\pi $
. Thus, in this case a rigid isomorphism
 $\mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
is the same as an isomorphism of transporter systems in the sense of [Reference Chermak6, Definition A.2] (which extends the definition of an isomorphism of linking systems in [Reference Broto, Levi and Oliver3, p. 799] and [Reference Aschbacher, Kessar and Oliver1, p. 146]).
$\mathcal {T}\longrightarrow {\widetilde {\mathcal {T}}}$
is the same as an isomorphism of transporter systems in the sense of [Reference Chermak6, Definition A.2] (which extends the definition of an isomorphism of linking systems in [Reference Broto, Levi and Oliver3, p. 799] and [Reference Aschbacher, Kessar and Oliver1, p. 146]).
4.2. The correspondence between transporter systems and localities
If
![]() $(\mathcal L,\Delta ,S)$
is a locality, then one can easily define a transporter system
$(\mathcal L,\Delta ,S)$
is a locality, then one can easily define a transporter system
![]() $\mathcal {T}_\Delta (\mathcal L)$
over
$\mathcal {T}_\Delta (\mathcal L)$
over
![]() $\mathcal {F}_S(\mathcal L)$
similarly as for groups; the object set of
$\mathcal {F}_S(\mathcal L)$
similarly as for groups; the object set of
![]() $\mathcal {T}_\Delta (\mathcal L)$
is
$\mathcal {T}_\Delta (\mathcal L)$
is
![]() $\Delta $
, and the morphism set between two objects P and Q consists of the triples
$\Delta $
, and the morphism set between two objects P and Q consists of the triples
![]() $(P,Q,g)$
, where
$(P,Q,g)$
, where
![]() $g\in \mathcal L$
with
$g\in \mathcal L$
with
![]() $P\subseteq \mathbf {D}(g^{-1})$
and
$P\subseteq \mathbf {D}(g^{-1})$
and
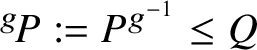 ${}^g\!P:=P^{g^{-1}}\leq Q$
. We will now outline how one can construct a locality from a transporter system.
${}^g\!P:=P^{g^{-1}}\leq Q$
. We will now outline how one can construct a locality from a transporter system.
Let
![]() $(\mathcal {T},\delta ,\pi )$
be a transporter system associated to a fusion system
$(\mathcal {T},\delta ,\pi )$
be a transporter system associated to a fusion system
![]() $\mathcal {F}$
. Denote the set of objects of
$\mathcal {F}$
. Denote the set of objects of
![]() $\mathcal {T}$
by
$\mathcal {T}$
by
![]() $\Delta $
and write
$\Delta $
and write
![]() $\mathrm {Iso}_{\mathcal {T}}(P,Q)$
for the set of isomorphisms between two objects P and Q and
$\mathrm {Iso}_{\mathcal {T}}(P,Q)$
for the set of isomorphisms between two objects P and Q and
![]() $\mathrm {Iso}(\mathcal {T}\;)$
for the set of all isomorphisms in
$\mathrm {Iso}(\mathcal {T}\;)$
for the set of all isomorphisms in
![]() $\mathcal {T}$
. By Reference Chermak[6] there is a partial order
$\mathcal {T}$
. By Reference Chermak[6] there is a partial order
![]() $\uparrow _{\mathcal {T}}$
defined on
$\uparrow _{\mathcal {T}}$
defined on
![]() $\mathrm {Iso}(\mathcal {T}\;)$
via
$\mathrm {Iso}(\mathcal {T}\;)$
via
![]() $\varphi _0\uparrow _{\mathcal {T}}\varphi $
if
$\varphi _0\uparrow _{\mathcal {T}}\varphi $
if
![]() $\varphi _0\in \mathrm {Iso}_{\mathcal {T}}(P_0,Q_0)$
,
$\varphi _0\in \mathrm {Iso}_{\mathcal {T}}(P_0,Q_0)$
,
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
,
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
,
![]() $P_0\leq P$
,
$P_0\leq P$
,
![]() $Q_0\leq Q$
and
$Q_0\leq Q$
and
Note that the latter condition means that
![]() $\varphi _0=\varphi |_{P_0,Q_0}$
.
$\varphi _0=\varphi |_{P_0,Q_0}$
.
Definition 4.3. Let
![]() $\mathcal L_\Delta (\mathcal {T}\;)$
be the set of equivalence classes of the elements of
$\mathcal L_\Delta (\mathcal {T}\;)$
be the set of equivalence classes of the elements of
![]() $\mathrm {Iso}(\mathcal {T}\;)$
with respect to the smallest equivalence relation on
$\mathrm {Iso}(\mathcal {T}\;)$
with respect to the smallest equivalence relation on
![]() $\mathrm {Iso}(\mathcal {T}\;)$
containing
$\mathrm {Iso}(\mathcal {T}\;)$
containing
![]() $\uparrow _{\mathcal {T}}$
. If
$\uparrow _{\mathcal {T}}$
. If
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and write
$\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and write
![]() $[\varphi ]$
for the equivalence class of
$[\varphi ]$
for the equivalence class of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal L_\Delta (\mathcal {T}\;)$
. By
$\mathcal L_\Delta (\mathcal {T}\;)$
. By
![]() $\mathbf {D}$
denote the set of tuples
$\mathbf {D}$
denote the set of tuples
![]() $w=(f_k,f_{k-1},\dots ,f_1)\in \mathbf {W}(\mathcal L_\Delta (\mathcal {T}\;))$
for which there exist
$w=(f_k,f_{k-1},\dots ,f_1)\in \mathbf {W}(\mathcal L_\Delta (\mathcal {T}\;))$
for which there exist
![]() $\varphi _i\in f_i$
for
$\varphi _i\in f_i$
for
![]() $i=1,\dots ,k$
such that the composition
$i=1,\dots ,k$
such that the composition
![]() $\varphi _k\circ \varphi _{k-1}\circ \cdots \circ \varphi _1$
is defined in the category
$\varphi _k\circ \varphi _{k-1}\circ \cdots \circ \varphi _1$
is defined in the category
![]() $\mathcal {T}$
. Moreover, given such w and
$\mathcal {T}$
. Moreover, given such w and
![]() $\varphi _i$
, set
$\varphi _i$
, set
![]() $\Pi (w):=[\varphi _k\circ \varphi _{k-1}\circ \cdots \circ \varphi _1]$
.
$\Pi (w):=[\varphi _k\circ \varphi _{k-1}\circ \cdots \circ \varphi _1]$
.
The map
![]() $\Pi \colon \mathbf {D}\longrightarrow \mathcal L_\Delta (\mathcal {T}\;)$
defined above is well defined. Together with
$\Pi \colon \mathbf {D}\longrightarrow \mathcal L_\Delta (\mathcal {T}\;)$
defined above is well defined. Together with
![]() $\Pi $
and the map
$\Pi $
and the map
![]() $\mathcal L\longrightarrow \mathcal L,[\varphi ]\mapsto [\varphi ^{-1}]$
(which is also well defined), the set
$\mathcal L\longrightarrow \mathcal L,[\varphi ]\mapsto [\varphi ^{-1}]$
(which is also well defined), the set
![]() $\mathcal L$
forms a partial group by [Reference Chermak6, Proposition A.9]. Moreover, the map
$\mathcal L$
forms a partial group by [Reference Chermak6, Proposition A.9]. Moreover, the map
is an injective homomorphism of partial groups, and its image
![]() $[S]$
is a subgroup of
$[S]$
is a subgroup of
![]() $\mathcal L_\Delta (\mathcal {T}\;)$
. Most of the time, we will identify
$\mathcal L_\Delta (\mathcal {T}\;)$
. Most of the time, we will identify
![]() $x\in S$
with
$x\in S$
with
![]() $[\delta _S(x)]\in [S]$
. With this identification, by [Reference Chermak6, Proposition A.13],
$[\delta _S(x)]\in [S]$
. With this identification, by [Reference Chermak6, Proposition A.13],
![]() $(\mathcal L_\Delta (\mathcal {T}\;),\Delta ,S)$
is a locality.
$(\mathcal L_\Delta (\mathcal {T}\;),\Delta ,S)$
is a locality.
Lemma 4.4. Let
![]() $(\mathcal {T},\delta ,\pi )$
be a transporter system associated to a fusion system
$(\mathcal {T},\delta ,\pi )$
be a transporter system associated to a fusion system
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
and
$\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
. As above, write
$\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
. As above, write
![]() $[\varphi ]$
for the equivalence class of
$[\varphi ]$
for the equivalence class of
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
in
$\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
in
![]() $\mathcal L$
. Then the following hold:
$\mathcal L$
. Then the following hold:
-
(a) If
 $P,Q\in \Delta $
,
$P,Q\in \Delta $
,
 $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
and
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
and
 $f=[\varphi ]$
, then
$f=[\varphi ]$
, then
 $P\subseteq S_{f^{-1}}$
,
$P\subseteq S_{f^{-1}}$
,
 ${}^f\!P=Q$
and
${}^f\!P=Q$
and
 $c_{f^{-1}}|_P=\pi (\varphi )$
.
$c_{f^{-1}}|_P=\pi (\varphi )$
. -
(b)
 $\mathrm {Aut}_{\mathcal {T}}(P)\cong N_{\mathcal L}(P)$
.
$\mathrm {Aut}_{\mathcal {T}}(P)\cong N_{\mathcal L}(P)$
. -
(c)
 $\mathcal {F}_S(\mathcal L)$
is the subsystem of
$\mathcal {F}_S(\mathcal L)$
is the subsystem of
 $\mathcal {F}$
generated by all of the sets
$\mathcal {F}$
generated by all of the sets
 $\mathrm {Hom}_{\mathcal {F}}(P,Q)$
with
$\mathrm {Hom}_{\mathcal {F}}(P,Q)$
with
 $P,Q\in \Delta $
.
$P,Q\in \Delta $
.
Proof. Let P, Q,
![]() $\varphi $
and f be as in (a), fix
$\varphi $
and f be as in (a), fix
![]() $x\in P$
and set
$x\in P$
and set
![]() $y:=\pi (\varphi )(x)\in Q$
. Observe that, via the usual identification of the elements of S with elements of
$y:=\pi (\varphi )(x)\in Q$
. Observe that, via the usual identification of the elements of S with elements of
![]() $\mathcal L$
, we have
$\mathcal L$
, we have
![]() $x=[\delta _S(x)]=[\delta _P(x)]$
, because
$x=[\delta _S(x)]=[\delta _P(x)]$
, because
![]() $\delta _S(x)\delta _{P,S}(1)=\delta _{P,S}(x)=\delta _{P,S}(1)\delta _P(x)$
. Similarly,
$\delta _S(x)\delta _{P,S}(1)=\delta _{P,S}(x)=\delta _{P,S}(1)\delta _P(x)$
. Similarly,
![]() $y=[\delta _S(y)]=[\delta _Q(y)]$
. Notice that the composition
$y=[\delta _S(y)]=[\delta _Q(y)]$
. Notice that the composition
![]() $\varphi \circ \delta _P(x)\circ \varphi ^{-1}$
is defined in
$\varphi \circ \delta _P(x)\circ \varphi ^{-1}$
is defined in
![]() $\mathcal L$
. Moreover, it follows from the definition of a transporter system (axiom (C) in [Reference Oliver and Ventura21, Definition 3.1]) that
$\mathcal L$
. Moreover, it follows from the definition of a transporter system (axiom (C) in [Reference Oliver and Ventura21, Definition 3.1]) that
![]() $\varphi \circ \delta _P(x)\circ \varphi ^{-1}=\delta _Q(y)$
. Hence,
$\varphi \circ \delta _P(x)\circ \varphi ^{-1}=\delta _Q(y)$
. Hence,
![]() $(f,x,f^{-1})=([\varphi ],[\delta _P(x)],[\varphi ^{-1}])\in \mathbf {D}$
and
$(f,x,f^{-1})=([\varphi ],[\delta _P(x)],[\varphi ^{-1}])\in \mathbf {D}$
and
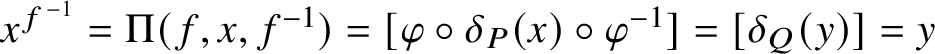 $x^{f^{-1}}=\Pi (f,x,f^{-1})=[\varphi \circ \delta _P(x)\circ \varphi ^{-1}]=[\delta _Q(y)]=y$
. This shows (a).
$x^{f^{-1}}=\Pi (f,x,f^{-1})=[\varphi \circ \delta _P(x)\circ \varphi ^{-1}]=[\delta _Q(y)]=y$
. This shows (a).
Property (a) yields in particular that the map
![]() $\alpha \colon \mathrm {Aut}_{\mathcal {T}}(P)\longrightarrow N_{\mathcal L}(P),\varphi \mapsto [\varphi ]$
is well defined. Moreover,
$\alpha \colon \mathrm {Aut}_{\mathcal {T}}(P)\longrightarrow N_{\mathcal L}(P),\varphi \mapsto [\varphi ]$
is well defined. Moreover,
![]() $\alpha $
is surjective by [Reference Chermak6, Corollary A.11] and injective by [Reference Chermak6, Lemma A.8(b)]. For all
$\alpha $
is surjective by [Reference Chermak6, Corollary A.11] and injective by [Reference Chermak6, Lemma A.8(b)]. For all
![]() $\varphi ,\psi \in \mathrm {Aut}(\mathcal {T}\;)$
, we have
$\varphi ,\psi \in \mathrm {Aut}(\mathcal {T}\;)$
, we have
![]() $\alpha (\varphi \circ \psi )=[\varphi \circ \psi ]=\Pi ([\varphi ],[\psi ])=\Pi (\alpha (\varphi ),\alpha (\psi ))$
. Hence,
$\alpha (\varphi \circ \psi )=[\varphi \circ \psi ]=\Pi ([\varphi ],[\psi ])=\Pi (\alpha (\varphi ),\alpha (\psi ))$
. Hence,
![]() $\alpha $
is an isomorphism of groups and (b) holds.
$\alpha $
is an isomorphism of groups and (b) holds.
To prove (c), notice that
![]() $\mathcal {F}_S(\mathcal L)$
is generated by all of the maps of the form
$\mathcal {F}_S(\mathcal L)$
is generated by all of the maps of the form
![]() $c_{f^{-1}}\colon P\longrightarrow Q$
, where
$c_{f^{-1}}\colon P\longrightarrow Q$
, where
![]() $P,Q\in \Delta $
,
$P,Q\in \Delta $
,
![]() $P\leq S_{f^{-1}}$
and
$P\leq S_{f^{-1}}$
and
![]() ${}^f\!P=Q$
. For such
${}^f\!P=Q$
. For such
![]() $P,Q,f$
, by [Reference Chermak6, Corollary A.11], there exists always
$P,Q,f$
, by [Reference Chermak6, Corollary A.11], there exists always
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
with
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
with
![]() $f=[\varphi ]$
. Moreover, the fusion system generated by the sets
$f=[\varphi ]$
. Moreover, the fusion system generated by the sets
![]() $\mathrm {Hom}_{\mathcal {F}}(P,Q)$
with
$\mathrm {Hom}_{\mathcal {F}}(P,Q)$
with
![]() $P,Q\in \Delta $
is actually generated by the sets
$P,Q\in \Delta $
is actually generated by the sets
![]() $\mathrm {Iso}_{\mathcal {F}}(P,Q)$
with
$\mathrm {Iso}_{\mathcal {F}}(P,Q)$
with
![]() $P,Q\in \Delta $
. Because
$P,Q\in \Delta $
. Because
![]() $\pi $
is surjective on morphism sets and, by [Reference Oliver and Ventura21, Lemma A.6], the preimages of isomorphisms in
$\pi $
is surjective on morphism sets and, by [Reference Oliver and Ventura21, Lemma A.6], the preimages of isomorphisms in
![]() $\mathcal {F}$
under
$\mathcal {F}$
under
![]() $\pi $
are isomorphisms in
$\pi $
are isomorphisms in
![]() $\mathcal {T}$
, property (c) follows from (a).
$\mathcal {T}$
, property (c) follows from (a).
If
![]() $\mathcal {C}$
is a small category and
$\mathcal {C}$
is a small category and
![]() $\Gamma \subseteq \mathrm {Ob}(\mathcal {C})$
, we will write
$\Gamma \subseteq \mathrm {Ob}(\mathcal {C})$
, we will write
![]() $\mathcal {C}|_\Gamma $
for the full subcategory of
$\mathcal {C}|_\Gamma $
for the full subcategory of
![]() $\mathcal {C}$
with object set
$\mathcal {C}$
with object set
![]() $\Gamma $
.
$\Gamma $
.
Lemma 4.5. Let
![]() $\mathcal {T}^{\;+}$
be a transporter system associated to a fusion system
$\mathcal {T}^{\;+}$
be a transporter system associated to a fusion system
![]() $\mathcal {F}$
and let
$\mathcal {F}$
and let
![]() $\Delta \subseteq \Delta ^+:=\mathrm {Ob}(\mathcal {T}^{\;+})$
such that
$\Delta \subseteq \Delta ^+:=\mathrm {Ob}(\mathcal {T}^{\;+})$
such that
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {F}$
-closed. Then
$\mathcal {F}$
-closed. Then
![]() $\mathcal {T}:=\mathcal {T}^{\;+}|_\Delta $
is a transporter system associated to
$\mathcal {T}:=\mathcal {T}^{\;+}|_\Delta $
is a transporter system associated to
![]() $\mathcal {F}$
. Moreover, writing
$\mathcal {F}$
. Moreover, writing
![]() $[\varphi ]_+$
for the equivalence class of
$[\varphi ]_+$
for the equivalence class of
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
in
$\varphi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
in
![]() $\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
and
$\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
and
![]() $[\varphi ]$
for the equivalence class of
$[\varphi ]$
for the equivalence class of
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
in
$\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
in
![]() $\mathcal L_\Delta (\mathcal {T}\;)$
, the map
$\mathcal L_\Delta (\mathcal {T}\;)$
, the map
is well defined and an isomorphism of partial groups, which restricts to the identity on S (if one identifies the elements of S with elements of
![]() $\mathcal L_\Delta (\mathcal {T}\;)$
and
$\mathcal L_\Delta (\mathcal {T}\;)$
and
![]() $\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
as usual).
$\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
as usual).
Proof. Because
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {F}$
-closed, it is immediate from the axioms of a transporter system that
$\mathcal {F}$
-closed, it is immediate from the axioms of a transporter system that
![]() $\mathcal {T}:=\mathcal {T}^{\;+}|_\Delta $
together with the restriction of
$\mathcal {T}:=\mathcal {T}^{\;+}|_\Delta $
together with the restriction of
![]() $\delta $
to
$\delta $
to
![]() $\mathcal {T}_\Delta (S)$
and the restriction of
$\mathcal {T}_\Delta (S)$
and the restriction of
![]() $\pi $
to
$\pi $
to
![]() $\mathcal {T}$
is a transporter system. Set
$\mathcal {T}$
is a transporter system. Set
![]() $\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
and
$\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
and
![]() $\mathcal L^+:=\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
. Write
$\mathcal L^+:=\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
. Write
![]() $\mathbf {D}$
for the domain of the partial product on
$\mathbf {D}$
for the domain of the partial product on
![]() $\mathcal L$
and
$\mathcal L$
and
![]() $\mathbf {D}':=\mathbf {D}_\Delta (\mathcal L^+)$
for the domain of the partial product on
$\mathbf {D}':=\mathbf {D}_\Delta (\mathcal L^+)$
for the domain of the partial product on
![]() $\mathcal L^+|_\Delta $
.
$\mathcal L^+|_\Delta $
.
If
![]() $\varphi ,\psi \in \mathrm {Iso}(\mathcal {T}\;)\subseteq \mathrm {Iso}(\mathcal {T}^{\;+})$
, then
$\varphi ,\psi \in \mathrm {Iso}(\mathcal {T}\;)\subseteq \mathrm {Iso}(\mathcal {T}^{\;+})$
, then
![]() $\varphi \uparrow _{\mathcal {T}}\psi $
implies
$\varphi \uparrow _{\mathcal {T}}\psi $
implies
![]() $\varphi \uparrow _{\mathcal {T}^{\;+}}\psi $
and so
$\varphi \uparrow _{\mathcal {T}^{\;+}}\psi $
and so
![]() $[\varphi ]=[\psi ]$
yields
$[\varphi ]=[\psi ]$
yields
![]() $[\varphi ]_+=[\psi ]_+$
. Hence, the map
$[\varphi ]_+=[\psi ]_+$
. Hence, the map
is well defined. It follows from the construction of the partial products on
![]() $\mathcal L=\mathcal L_\Delta (\mathcal {T}\;)$
and
$\mathcal L=\mathcal L_\Delta (\mathcal {T}\;)$
and
![]() $\mathcal L^+=\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
that
$\mathcal L^+=\mathcal L_{\Delta ^+}(\mathcal {T}^{\;+})$
that
![]() $\iota $
is a homomorphism of partial groups. Moreover, because we identify every element
$\iota $
is a homomorphism of partial groups. Moreover, because we identify every element
![]() $x\in S$
with
$x\in S$
with
![]() $[\delta _S(x)]\in \mathcal L$
and with
$[\delta _S(x)]\in \mathcal L$
and with
![]() $[\delta _S(x)]_+\in \mathcal L^+$
, the map
$[\delta _S(x)]_+\in \mathcal L^+$
, the map
![]() $\iota '$
restricts to the identity on S. In particular, because
$\iota '$
restricts to the identity on S. In particular, because
![]() $(\mathcal L,\Delta ,S)$
is a locality, it follows that
$(\mathcal L,\Delta ,S)$
is a locality, it follows that
![]() $\iota '(\mathcal L)\subseteq \mathcal L^+|_\Delta $
and
$\iota '(\mathcal L)\subseteq \mathcal L^+|_\Delta $
and
![]() $(\iota ')^*(\mathbf {D})\subseteq \mathbf {D}'=\mathbf {D}_\Delta (\mathcal L^+)$
(with
$(\iota ')^*(\mathbf {D})\subseteq \mathbf {D}'=\mathbf {D}_\Delta (\mathcal L^+)$
(with
![]() $(\iota ')^*$
defined as in Definition 2.16 but written on the left). Hence,
$(\iota ')^*$
defined as in Definition 2.16 but written on the left). Hence,
![]() $\iota $
is well defined and a homomorphism of partial groups. It remains to show that
$\iota $
is well defined and a homomorphism of partial groups. It remains to show that
![]() $\iota $
is injective and
$\iota $
is injective and
![]() $\mathbf {D}'\subseteq \iota ^*(\mathbf {D})$
.
$\mathbf {D}'\subseteq \iota ^*(\mathbf {D})$
.
If
![]() $\varphi \uparrow _{\mathcal {T}^{\;+}}\chi $
for some
$\varphi \uparrow _{\mathcal {T}^{\;+}}\chi $
for some
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and
$\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and
![]() $\chi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
, then the assumption that
$\chi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
, then the assumption that
![]() $\Delta $
is overgroup closed in S implies
$\Delta $
is overgroup closed in S implies
![]() $\chi \in \mathrm {Iso}(\mathcal {T}\;)$
and
$\chi \in \mathrm {Iso}(\mathcal {T}\;)$
and
![]() $\varphi \uparrow _{\mathcal {T}}\chi $
. By [Reference Chermak6, Lemma A.8(a)], every element of
$\varphi \uparrow _{\mathcal {T}}\chi $
. By [Reference Chermak6, Lemma A.8(a)], every element of
![]() $\mathcal L^+$
contains a unique maximal element with respect to the partial order
$\mathcal L^+$
contains a unique maximal element with respect to the partial order
![]() $\uparrow _{\mathcal {T}^{\;+}}$
. So if
$\uparrow _{\mathcal {T}^{\;+}}$
. So if
![]() $[\varphi ]_+=[\psi ]_+$
for some
$[\varphi ]_+=[\psi ]_+$
for some
![]() $\varphi ,\psi \in \mathrm {Iso}(\mathcal {T}\;)$
, then for the
$\varphi ,\psi \in \mathrm {Iso}(\mathcal {T}\;)$
, then for the
![]() $\uparrow _{\mathcal {T}^{\;+}}$
-maximal element
$\uparrow _{\mathcal {T}^{\;+}}$
-maximal element
![]() $\chi $
of
$\chi $
of
![]() $[\varphi ]_+=[\psi ]_+$
we have
$[\varphi ]_+=[\psi ]_+$
we have
![]() $\chi \in \mathrm {Iso}(\mathcal {T}\;)$
,
$\chi \in \mathrm {Iso}(\mathcal {T}\;)$
,
![]() $\varphi \uparrow _{\mathcal {T}}\chi $
and
$\varphi \uparrow _{\mathcal {T}}\chi $
and
![]() $\psi \uparrow _{\mathcal {T}}\chi $
. Hence,
$\psi \uparrow _{\mathcal {T}}\chi $
. Hence,
![]() $[\varphi ]=[\psi ]$
, which proves that
$[\varphi ]=[\psi ]$
, which proves that
![]() $\iota $
is injective.
$\iota $
is injective.
If
![]() $P,Q\in \Delta $
and
$P,Q\in \Delta $
and
![]() $f\in \mathcal L^+$
with
$f\in \mathcal L^+$
with
![]() ${}^f\!P=Q$
, then by [Reference Chermak6, Corollary A.11], there exists
${}^f\!P=Q$
, then by [Reference Chermak6, Corollary A.11], there exists
![]() $\psi \in \mathrm {Iso}_{\mathcal {T}^{\;+}}(P,Q)$
with
$\psi \in \mathrm {Iso}_{\mathcal {T}^{\;+}}(P,Q)$
with
![]() $f=[\psi ]_+$
. For such
$f=[\psi ]_+$
. For such
![]() $\psi $
, we have
$\psi $
, we have
![]() $\psi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
and
$\psi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
and
![]() $\iota ([\psi ])=f$
. From this property, the definition of
$\iota ([\psi ])=f$
. From this property, the definition of
![]() $\mathbf {D}$
and the definition of
$\mathbf {D}$
and the definition of
![]() $\mathbf {D}'=\mathbf {D}_\Delta (\mathcal L^+)$
, one sees that
$\mathbf {D}'=\mathbf {D}_\Delta (\mathcal L^+)$
, one sees that
![]() $\mathbf {D}'\subseteq \iota ^*(\mathbf {D})$
. Hence, the assertion holds.
$\mathbf {D}'\subseteq \iota ^*(\mathbf {D})$
. Hence, the assertion holds.
Lemma 4.6. Let
![]() $(\mathcal {T},\delta ,\pi )$
and
$(\mathcal {T},\delta ,\pi )$
and
![]() $({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
be transporter systems associated to fusion systems
$({\widetilde {\mathcal {T}}},{\tilde {\delta }},{\tilde {\pi }})$
be transporter systems associated to fusion systems
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() ${\widetilde {\mathcal {F}}}$
over p-groups S and
${\widetilde {\mathcal {F}}}$
over p-groups S and
![]() ${\widetilde {S}}$
, respectively. Set
${\widetilde {S}}$
, respectively. Set
![]() $\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
,
$\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
,
![]() $\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
,
$\mathcal L:=\mathcal L_\Delta (\mathcal {T}\;)$
,
![]() $\widetilde {\Delta }=\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
and
$\widetilde {\Delta }=\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
and
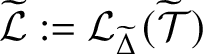 ${\widetilde {\mathcal {L}}}:=\mathcal L_{\widetilde {\Delta }}({\widetilde {\mathcal {T}}}\;)$
. For
${\widetilde {\mathcal {L}}}:=\mathcal L_{\widetilde {\Delta }}({\widetilde {\mathcal {T}}}\;)$
. For
![]() $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
define
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
define
![]() $\Lambda (\alpha )\colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
to be the map that, for all
$\Lambda (\alpha )\colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
to be the map that, for all
![]() $P,Q\in \Delta $
and all
$P,Q\in \Delta $
and all
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
, sends the class
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
, sends the class
![]() $[\varphi ]\in \mathcal L$
to the class
$[\varphi ]\in \mathcal L$
to the class
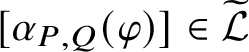 $[\alpha _{P,Q}(\varphi )]\in {\widetilde {\mathcal {L}}}$
. Then this defines a bijection
$[\alpha _{P,Q}(\varphi )]\in {\widetilde {\mathcal {L}}}$
. Then this defines a bijection
Moreover, if
![]() $\Gamma $
and
$\Gamma $
and
![]() $\widetilde {\Gamma }$
are sets of subgroups of S and
$\widetilde {\Gamma }$
are sets of subgroups of S and
![]() ${\widetilde {S}}$
, respectively, then
${\widetilde {S}}$
, respectively, then
![]() $\Lambda $
induces a bijection
$\Lambda $
induces a bijection
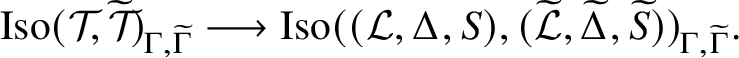 $$ \begin{align*}\mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}})_{\Gamma,\widetilde{\Gamma}}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Gamma,\widetilde{\Gamma}}.\end{align*} $$
$$ \begin{align*}\mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}})_{\Gamma,\widetilde{\Gamma}}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Gamma,\widetilde{\Gamma}}.\end{align*} $$
Proof. By [Reference Glauberman and Lynd12, Theorem 2.11] and the proof of this result, there is an equivalence
![]() $\Lambda '$
from the category of transporter systems with isomorphisms to the category of localities with isomorphisms, which is defined on objects by sending a transporter system
$\Lambda '$
from the category of transporter systems with isomorphisms to the category of localities with isomorphisms, which is defined on objects by sending a transporter system
![]() $\mathcal {T}$
to
$\mathcal {T}$
to
![]() $\mathcal L_{\mathrm {Ob}(\mathcal {T}\;)}(\mathcal {T}\;)$
and on morphisms by sending an isomorphism
$\mathcal L_{\mathrm {Ob}(\mathcal {T}\;)}(\mathcal {T}\;)$
and on morphisms by sending an isomorphism
![]() $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
to
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
to
![]() $\Lambda (\alpha )$
as defined in the theorem. In particular,
$\Lambda (\alpha )$
as defined in the theorem. In particular,
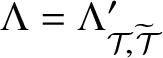 $\Lambda =\Lambda ^{\prime }_{\mathcal {T},{\widetilde {\mathcal {T}}}}$
is a bijection
$\Lambda =\Lambda ^{\prime }_{\mathcal {T},{\widetilde {\mathcal {T}}}}$
is a bijection
![]() $\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})\longrightarrow \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))$
.
$\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})\longrightarrow \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))$
.
Let now
![]() $P\leq S$
and
$P\leq S$
and
![]() $Q\leq {\widetilde {S}}$
. Via the usual identifications of the elements of S and
$Q\leq {\widetilde {S}}$
. Via the usual identifications of the elements of S and
![]() ${\widetilde {S}}$
with elements of
${\widetilde {S}}$
with elements of
![]() $\mathcal L$
and
$\mathcal L$
and
![]() ${\widetilde {\mathcal {L}}}$
, we have
${\widetilde {\mathcal {L}}}$
, we have
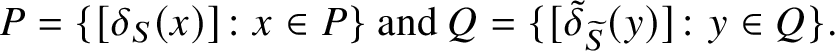 $$ \begin{align*}P=\{[\delta_S(x)]\colon x\in P\}\mbox{ and }Q=\{[{\tilde{\delta}}_{\widetilde{S}}(y)]\colon y\in Q\}.\end{align*} $$
$$ \begin{align*}P=\{[\delta_S(x)]\colon x\in P\}\mbox{ and }Q=\{[{\tilde{\delta}}_{\widetilde{S}}(y)]\colon y\in Q\}.\end{align*} $$
So given
![]() $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
,
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})$
,
Because the map
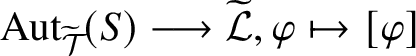 $\mathrm {Aut}_{{\widetilde {\mathcal {T}}}}(S)\longrightarrow {\widetilde {\mathcal {L}}},\varphi \mapsto [\varphi ]$
is by [Reference Chermak6, Lemma A.8(b)] injective, it follows that
$\mathrm {Aut}_{{\widetilde {\mathcal {T}}}}(S)\longrightarrow {\widetilde {\mathcal {L}}},\varphi \mapsto [\varphi ]$
is by [Reference Chermak6, Lemma A.8(b)] injective, it follows that
![]() $\Lambda (\alpha )(P)=Q$
if and only if
$\Lambda (\alpha )(P)=Q$
if and only if
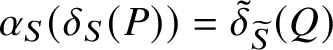 $\alpha _S(\delta _S(P))={\tilde {\delta }}_{\widetilde {S}}(Q)$
. So
$\alpha _S(\delta _S(P))={\tilde {\delta }}_{\widetilde {S}}(Q)$
. So
![]() $\Lambda (\alpha )(\Gamma ):=\{\Lambda (\alpha )(P)\colon P\in \Gamma \}$
equals
$\Lambda (\alpha )(\Gamma ):=\{\Lambda (\alpha )(P)\colon P\in \Gamma \}$
equals
![]() $\widetilde {\Gamma }$
if and only if
$\widetilde {\Gamma }$
if and only if
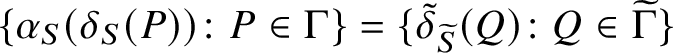 $\{\alpha _S(\delta _S(P))\colon P\in \Gamma \}=\{{\tilde {\delta }}_{\widetilde {S}}(Q)\colon Q\in \widetilde {\Gamma }\}$
. Equivalently,
$\{\alpha _S(\delta _S(P))\colon P\in \Gamma \}=\{{\tilde {\delta }}_{\widetilde {S}}(Q)\colon Q\in \widetilde {\Gamma }\}$
. Equivalently,
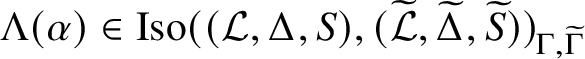 $\Lambda (\alpha )\in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Gamma ,\widetilde {\Gamma }}$
if and only if
$\Lambda (\alpha )\in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Gamma ,\widetilde {\Gamma }}$
if and only if
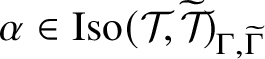 $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
. (Unlike in Definition 2.20, we write maps here on the right.)
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Gamma ,\widetilde {\Gamma }}$
. (Unlike in Definition 2.20, we write maps here on the right.)
4.3. Linking systems
In this article we work with the following definition of a linking system, which is slightly nonstandard but fits well with the earlier given definition of a linking locality (Definition 2.25).
Definition 4.7. If
![]() $\mathcal {F}$
is a saturated fusion system, then a linking system associated to
$\mathcal {F}$
is a saturated fusion system, then a linking system associated to
![]() $\mathcal {F}$
is a transporter system
$\mathcal {F}$
is a transporter system
![]() $\mathcal {T}$
associated to
$\mathcal {T}$
associated to
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
$\mathcal {F}^{cr}\subseteq \mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Aut}_{\mathcal {T}}(P)$
is of characteristic p for every
$\mathrm {Aut}_{\mathcal {T}}(P)$
is of characteristic p for every
![]() $P\in \mathrm {Ob}(\mathcal {T}\;)$
. If
$P\in \mathrm {Ob}(\mathcal {T}\;)$
. If
![]() $\mathrm {Ob}(\mathcal {T}\;)=\mathcal {F}^s$
, then
$\mathrm {Ob}(\mathcal {T}\;)=\mathcal {F}^s$
, then
![]() $\mathcal {T}$
is called a subcentric linking system associated to
$\mathcal {T}$
is called a subcentric linking system associated to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
The original definitions of linking systems in Reference Broto, Levi and Oliver[3], Reference Broto, Castellana, Grodal, Levi and Oliver[4] and Reference Oliver[19] are not based on the definition of a transporter systems. A linking system in either of these definitions is a linking system in the above definition, whereas the converse does not hold in general. Historically, centric linking systems – that is, linking systems over
![]() $\mathcal {F}$
whose object sets are the sets of
$\mathcal {F}$
whose object sets are the sets of
![]() $\mathcal {F}$
-centric subgroups – were studied first. The long-standing conjecture that there is a centric linking system associated to every saturated fusion system and that such a centric linking system is unique up to a rigid isomorphism was shown by Chermak Reference Chermak[6] and subsequently by Oliver Reference Oliver[20]. Originally, these proofs used the classification of finite simple groups, but the dependence on the classification of the proof in Reference Oliver[20] was removed by Glauberman–Lynd Reference Glauberman and Lynd[11].
$\mathcal {F}$
-centric subgroups – were studied first. The long-standing conjecture that there is a centric linking system associated to every saturated fusion system and that such a centric linking system is unique up to a rigid isomorphism was shown by Chermak Reference Chermak[6] and subsequently by Oliver Reference Oliver[20]. Originally, these proofs used the classification of finite simple groups, but the dependence on the classification of the proof in Reference Oliver[20] was removed by Glauberman–Lynd Reference Glauberman and Lynd[11].
If
![]() $\mathcal {T}$
is a linking system associated to a saturated fusion system
$\mathcal {T}$
is a linking system associated to a saturated fusion system
![]() $\mathcal {F}$
over S, then
$\mathcal {F}$
over S, then
![]() $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathcal {F}^s$
. On the other hand, if
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathcal {F}^s$
. On the other hand, if
![]() $\mathcal {F}^{cr}\subseteq \Delta \subseteq \mathcal {F}^s$
such that
$\mathcal {F}^{cr}\subseteq \Delta \subseteq \mathcal {F}^s$
such that
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {F}$
-closed, then it was stated in [Reference Henke14, Theorem A] that there is a linking system
$\mathcal {F}$
-closed, then it was stated in [Reference Henke14, Theorem A] that there is a linking system
![]() $\mathcal {T}$
with object set
$\mathcal {T}$
with object set
![]() $\Delta $
associated to
$\Delta $
associated to
![]() $\mathcal {F}$
; moreover, such
$\mathcal {F}$
; moreover, such
![]() $\mathcal {T}$
is unique up to rigid isomorphism. The proof relies heavily on the existence and uniqueness of centric linking systems. Formally, [Reference Henke14, Theorem A] is proved as a consequence of the corresponding statement about linking localities that is summarised in Subsection 2.7. We use this opportunity to point out that a precise argument that
$\mathcal {T}$
is unique up to rigid isomorphism. The proof relies heavily on the existence and uniqueness of centric linking systems. Formally, [Reference Henke14, Theorem A] is proved as a consequence of the corresponding statement about linking localities that is summarised in Subsection 2.7. We use this opportunity to point out that a precise argument that
![]() $\mathcal {T}$
is unique up to a rigid isomorphism is actually missing in Reference Henke[14]. However, the uniqueness of
$\mathcal {T}$
is unique up to a rigid isomorphism is actually missing in Reference Henke[14]. However, the uniqueness of
![]() $\mathcal {T}$
follows from [Reference Glauberman and Lynd12, Theorem 2.11] (or [Reference Chermak6, Lemma A.14, Lemma A.15]) and from Lemma 4.8.
$\mathcal {T}$
follows from [Reference Glauberman and Lynd12, Theorem 2.11] (or [Reference Chermak6, Lemma A.14, Lemma A.15]) and from Lemma 4.8.
If
![]() $(\mathcal L,\Delta ,S)$
is a locality over
$(\mathcal L,\Delta ,S)$
is a locality over
![]() $\mathcal {F}$
, then it is easy to see that the corresponding transporter system
$\mathcal {F}$
, then it is easy to see that the corresponding transporter system
![]() $\mathcal {T}_\Delta (\mathcal L)$
is a linking system associated to
$\mathcal {T}_\Delta (\mathcal L)$
is a linking system associated to
![]() $\mathcal {F}$
if and only if
$\mathcal {F}$
if and only if
![]() $(\mathcal L,\Delta ,S)$
is a linking locality. Moreover, we have the following lemma.
$(\mathcal L,\Delta ,S)$
is a linking locality. Moreover, we have the following lemma.
Lemma 4.8. If
![]() $\mathcal {T}$
is a linking system associated to a saturated fusion system
$\mathcal {T}$
is a linking system associated to a saturated fusion system
![]() $\mathcal {F}$
, then for
$\mathcal {F}$
, then for
![]() $\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
, the locality
$\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
, the locality
![]() $(\mathcal L_\Delta (\mathcal {T}\;),\Delta ,S)$
is a linking locality over
$(\mathcal L_\Delta (\mathcal {T}\;),\Delta ,S)$
is a linking locality over
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Proof. Because
![]() $\mathcal {F}^{cr}\subseteq \Delta $
, it follows from Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver1, Theorem I.3.6] and Lemma 4.4(c) that
$\mathcal {F}^{cr}\subseteq \Delta $
, it follows from Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver1, Theorem I.3.6] and Lemma 4.4(c) that
![]() $\mathcal {F}_S(\mathcal L)=\mathcal {F}$
. In particular,
$\mathcal {F}_S(\mathcal L)=\mathcal {F}$
. In particular,
![]() $\mathcal {F}_S(\mathcal L)$
is saturated and
$\mathcal {F}_S(\mathcal L)$
is saturated and
![]() $\mathcal {F}_S(\mathcal L)^{cr}\subseteq \Delta $
. Moreover, by Lemma 4.4(b),
$\mathcal {F}_S(\mathcal L)^{cr}\subseteq \Delta $
. Moreover, by Lemma 4.4(b),
![]() $N_{\mathcal L}(P)\cong \mathrm {Aut}_{\mathcal {T}}(P)$
is of characteristic p for every
$N_{\mathcal L}(P)\cong \mathrm {Aut}_{\mathcal {T}}(P)$
is of characteristic p for every
![]() $P\in \Delta $
.
$P\in \Delta $
.
Lemma 4.9. If
![]() $(\mathcal {T},\delta ,\pi )$
is a linking system associated to a saturated fusion system
$(\mathcal {T},\delta ,\pi )$
is a linking system associated to a saturated fusion system
![]() $\mathcal {F}$
over S, then the following hold:
$\mathcal {F}$
over S, then the following hold:
-
(a)
 $\ker (\pi _S)=\delta _S(Z(S))$
.
$\ker (\pi _S)=\delta _S(Z(S))$
. -
(b) For every
 $P\in \mathrm {Ob}(\mathcal {T}\;)$
,
$P\in \mathrm {Ob}(\mathcal {T}\;)$
,
 $O_p(\mathrm {Aut}_{\mathcal {T}}(P))=\delta _P(P)$
if and only if
$O_p(\mathrm {Aut}_{\mathcal {T}}(P))=\delta _P(P)$
if and only if
 $P\in \mathcal {F}^{cr}$
.
$P\in \mathcal {F}^{cr}$
. -
(c) (Alperin’s fusion theorem for linking systems) Each morphism in
 $\mathcal {T}$
is the composite of restrictions of elements in the automorphism groups
$\mathcal {T}$
is the composite of restrictions of elements in the automorphism groups
 $\mathrm {Aut}_{\mathcal {T}}(P)$
, where
$\mathrm {Aut}_{\mathcal {T}}(P)$
, where
 $P\in \mathcal {F}^{cr}$
is fully
$P\in \mathcal {F}^{cr}$
is fully
 $\mathcal {F}$
-normalised.
$\mathcal {F}$
-normalised.
Proof. If
![]() $\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
, then for all
$\gamma \in \mathrm {Aut}_{\mathcal {T}}(S)$
, then for all
![]() $g\in S$
,
$g\in S$
,
![]() $\pi _S(\gamma )(g)=g$
if and only if
$\pi _S(\gamma )(g)=g$
if and only if
![]() $\gamma $
commutes with
$\gamma $
commutes with
![]() $\delta _S(g)$
by Axiom C in [Reference Oliver and Ventura21, Definition 3.1] and [Reference Oliver and Ventura21, Lemma 3.3]. Hence,
$\delta _S(g)$
by Axiom C in [Reference Oliver and Ventura21, Definition 3.1] and [Reference Oliver and Ventura21, Lemma 3.3]. Hence,
![]() $\ker (\pi _S)=C_{\mathrm {Aut}_{\mathcal {T}}(S)}(\delta _S(S))$
. Because
$\ker (\pi _S)=C_{\mathrm {Aut}_{\mathcal {T}}(S)}(\delta _S(S))$
. Because
![]() $\mathrm {Aut}_{\mathcal {T}}(S)$
is of characteristic p and
$\mathrm {Aut}_{\mathcal {T}}(S)$
is of characteristic p and
![]() $\delta _S(S)$
is a normal Sylow p-subgroup of
$\delta _S(S)$
is a normal Sylow p-subgroup of
![]() $\mathrm {Aut}_{\mathcal {T}}(S)$
, we have
$\mathrm {Aut}_{\mathcal {T}}(S)$
, we have
![]() $\gamma \in C_{\mathrm {Aut}_{\mathcal {T}}(S)}(\delta _S(S))=Z(\delta _S(S))=\delta _S(Z(S))$
showing (a).
$\gamma \in C_{\mathrm {Aut}_{\mathcal {T}}(S)}(\delta _S(S))=Z(\delta _S(S))=\delta _S(Z(S))$
showing (a).
Property (b) follows from [Reference Henke14, Lemma 6.2] and Lemma 4.8 or, alternatively, this property can be shown by reformulating the argument in the proof of [Reference Henke14, Lemma 6.2] for transporter systems. Property (c) follows from (b) and [Reference Oliver and Ventura21, Proposition 3.9].
Lemma 4.10. If
![]() $(\mathcal {T},\delta ,\pi )$
is a linking system associated to a saturated fusion system
$(\mathcal {T},\delta ,\pi )$
is a linking system associated to a saturated fusion system
![]() $\mathcal {F}$
over S, then the sequence
$\mathcal {F}$
over S, then the sequence
 $$ \begin{align*}1\longrightarrow Z(\mathcal{F}\;)\xrightarrow{\;\;\delta_S\;\;} \mathrm{Aut}_{\mathcal{T}}\;(S)\xrightarrow{\;\gamma\mapsto c_\gamma\;} \mathrm{Aut}(\mathcal{T}\;)\longrightarrow \mathrm{Out}_{{\operatorname{typ}}}(\mathcal{T}\;)\longrightarrow 1 \end{align*} $$
$$ \begin{align*}1\longrightarrow Z(\mathcal{F}\;)\xrightarrow{\;\;\delta_S\;\;} \mathrm{Aut}_{\mathcal{T}}\;(S)\xrightarrow{\;\gamma\mapsto c_\gamma\;} \mathrm{Aut}(\mathcal{T}\;)\longrightarrow \mathrm{Out}_{{\operatorname{typ}}}(\mathcal{T}\;)\longrightarrow 1 \end{align*} $$
is exact.
Proof. The statement was shown in [Reference Andersen, Oliver and Ventura2, Lemma 1.14(a)] for linking systems in Oliver’s definition; that is, for linking systems whose objects are quasicentric subgroups. The argument can be repeated verbatim (with
![]() $\mathcal L$
replaced by
$\mathcal L$
replaced by
![]() $\mathcal {T}$
) to prove exactness in
$\mathcal {T}$
) to prove exactness in
![]() $\mathrm {Aut}(\mathcal {T}\;)$
and in
$\mathrm {Aut}(\mathcal {T}\;)$
and in
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
and to show that
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
and to show that
![]() $c_\gamma =\operatorname {id}_{\mathcal {T}}$
implies
$c_\gamma =\operatorname {id}_{\mathcal {T}}$
implies
![]() $\gamma \in \delta _S(Z(\mathcal {F}))$
; here only the reference to [Reference Andersen, Oliver and Ventura2, Lemma 1.11(b’)] needs to be replaced by a reference to [Reference Oliver and Ventura21, Lemma 3.2(c)], the reference to axiom (A) needs to be replaced by a reference to Lemma 4.9(a), and the reference to [Reference Andersen, Oliver and Ventura2, Lemma 1.11(e)] needs to be replaced by a reference to axiom (II) in the definition of a transporter system [Reference Oliver and Ventura21, Definition 3.1]. On the other hand, by [Reference Aschbacher, Kessar and Oliver1, Proposition 4.5], we have
$\gamma \in \delta _S(Z(\mathcal {F}))$
; here only the reference to [Reference Andersen, Oliver and Ventura2, Lemma 1.11(b’)] needs to be replaced by a reference to [Reference Oliver and Ventura21, Lemma 3.2(c)], the reference to axiom (A) needs to be replaced by a reference to Lemma 4.9(a), and the reference to [Reference Andersen, Oliver and Ventura2, Lemma 1.11(e)] needs to be replaced by a reference to axiom (II) in the definition of a transporter system [Reference Oliver and Ventura21, Definition 3.1]. On the other hand, by [Reference Aschbacher, Kessar and Oliver1, Proposition 4.5], we have
![]() $Z(\mathcal {F})\leq P$
for all
$Z(\mathcal {F})\leq P$
for all
![]() $P\in \mathcal {F}^{cr}$
. So if
$P\in \mathcal {F}^{cr}$
. So if
![]() $a\in Z(\mathcal {F})$
, then Lemma 4.9(c) yields that any morphism
$a\in Z(\mathcal {F})$
, then Lemma 4.9(c) yields that any morphism
![]() $\psi \in \mathrm {Mor}_{\mathcal L}(P,Q)$
extends to a morphism
$\psi \in \mathrm {Mor}_{\mathcal L}(P,Q)$
extends to a morphism
![]() $\overline {\psi }\in \mathrm {Mor}_{\mathcal L}(\langle P,a\rangle ,\langle Q,a\rangle )$
with
$\overline {\psi }\in \mathrm {Mor}_{\mathcal L}(\langle P,a\rangle ,\langle Q,a\rangle )$
with
![]() $\pi (\overline {\psi })(a)=a$
. Such
$\pi (\overline {\psi })(a)=a$
. Such
![]() $\overline {\psi }$
commutes with
$\overline {\psi }$
commutes with
![]() $\gamma =\delta _S(a)$
by axiom (C) again. So
$\gamma =\delta _S(a)$
by axiom (C) again. So
![]() $\gamma $
commutes with
$\gamma $
commutes with
![]() $\psi $
and thus
$\psi $
and thus
![]() $c_\gamma =\operatorname {id}_{\mathcal L}$
. This shows exactness in
$c_\gamma =\operatorname {id}_{\mathcal L}$
. This shows exactness in
![]() $\mathrm {Aut}_{\mathcal {T}}(S)$
.
$\mathrm {Aut}_{\mathcal {T}}(S)$
.
5. Isomorphisms between linking localities and linking systems
In this section we prove Theorems A.1 and A.2. Moreover, we show considerably more general versions of these theorems, where for each result we formulate a version for linking localities and a version for linking systems. Theorem A.2 leads naturally to a statement about outer automorphism groups (Theorem 5.5), and building on this we prove Theorem B.
Theorem 5.1 Linking locality version
Let
![]() $(\mathcal L,\Delta ,S)$
,
$(\mathcal L,\Delta ,S)$
,
![]() $(\mathcal L^+,\Delta ^+,S)$
,
$(\mathcal L^+,\Delta ^+,S)$
,
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
and
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
and
 $({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}})$
be linking localities such that
$({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}})$
be linking localities such that
-
•
 $\mathcal {F}_S(\mathcal L^+)=\mathcal {F}_S(\mathcal L)$
,
$\mathcal {F}_S(\mathcal L^+)=\mathcal {F}_S(\mathcal L)$
,
 $\Delta \subseteq \Delta ^+$
,
$\Delta \subseteq \Delta ^+$
,
 $\mathcal L=\mathcal L^+|_\Delta $
and
$\mathcal L=\mathcal L^+|_\Delta $
and -
•
 $\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}}^+)=\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
,
$\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}}^+)=\mathcal {F}_{{\widetilde {S}}}({\widetilde {\mathcal {L}}})$
,
 $\widetilde {\Delta }\subseteq \widetilde {\Delta }^+$
,
$\widetilde {\Delta }\subseteq \widetilde {\Delta }^+$
,
 ${\widetilde {\mathcal {L}}}={\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }}$
.
${\widetilde {\mathcal {L}}}={\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }}$
.
Then the map
 $$ \begin{align*}\Psi\colon \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
$$ \begin{align*}\Psi\colon \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
with
![]() $\Psi (\gamma )=\gamma |_{\mathcal L}$
is well defined and a bijection.
$\Psi (\gamma )=\gamma |_{\mathcal L}$
is well defined and a bijection.
Proof. By Lemma 2.24, the map
![]() $\Psi $
is well defined. If
$\Psi $
is well defined. If
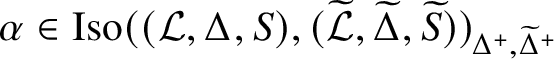 $\alpha \in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
, then
$\alpha \in \mathrm {Iso}((\mathcal L,\Delta ,S),({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
, then
![]() $\alpha $
regarded as a map
$\alpha $
regarded as a map
![]() $\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}^+$
is a homomorphism of partial groups. Thus, by Corollary 3.3,
$\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}^+$
is a homomorphism of partial groups. Thus, by Corollary 3.3,
![]() $\alpha $
extends to a unique homomorphism of partial groups
$\alpha $
extends to a unique homomorphism of partial groups
 $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
. By Lemma 2.18,
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
. By Lemma 2.18,
![]() $\alpha ^{-1}$
is a homomorphism of partial groups from
$\alpha ^{-1}$
is a homomorphism of partial groups from
![]() ${\widetilde {\mathcal {L}}}$
to
${\widetilde {\mathcal {L}}}$
to
![]() $\mathcal L$
, which can be regarded as a homomorphism of partial groups
$\mathcal L$
, which can be regarded as a homomorphism of partial groups
![]() ${\widetilde {\mathcal {L}}}\longrightarrow \mathcal L^+$
. So again by Corollary 3.3,
${\widetilde {\mathcal {L}}}\longrightarrow \mathcal L^+$
. So again by Corollary 3.3,
![]() $\alpha ^{-1}$
extends to a homomorphism of partial groups
$\alpha ^{-1}$
extends to a homomorphism of partial groups
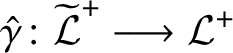 $\hat {\gamma }\colon {\widetilde {\mathcal {L}}}^+\longrightarrow \mathcal L^+$
. Then
$\hat {\gamma }\colon {\widetilde {\mathcal {L}}}^+\longrightarrow \mathcal L^+$
. Then
![]() $\gamma \hat {\gamma }\colon \mathcal L^+\longrightarrow \mathcal L^+$
and
$\gamma \hat {\gamma }\colon \mathcal L^+\longrightarrow \mathcal L^+$
and
 $\hat {\gamma }\gamma \colon {\widetilde {\mathcal {L}}}^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
are homomorphisms of partial groups with
$\hat {\gamma }\gamma \colon {\widetilde {\mathcal {L}}}^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
are homomorphisms of partial groups with
![]() $(\gamma \hat {\gamma })|_{\mathcal L}=\alpha \alpha ^{-1}=\operatorname {id}_{\mathcal L}$
and
$(\gamma \hat {\gamma })|_{\mathcal L}=\alpha \alpha ^{-1}=\operatorname {id}_{\mathcal L}$
and
 $(\hat {\gamma }\gamma )|_{{\widetilde {\mathcal {L}}}}=\alpha ^{-1}\alpha =\operatorname {id}_{{\widetilde {\mathcal {L}}}}$
. It follows from Corollary 3.3 applied with
$(\hat {\gamma }\gamma )|_{{\widetilde {\mathcal {L}}}}=\alpha ^{-1}\alpha =\operatorname {id}_{{\widetilde {\mathcal {L}}}}$
. It follows from Corollary 3.3 applied with
![]() $\operatorname {id}_{\mathcal L}$
in place of
$\operatorname {id}_{\mathcal L}$
in place of
![]() $\alpha $
that there is a unique homomorphism of partial groups
$\alpha $
that there is a unique homomorphism of partial groups
![]() $\mathcal L^+\longrightarrow \mathcal L^+$
that restricts to the identity on
$\mathcal L^+\longrightarrow \mathcal L^+$
that restricts to the identity on
![]() $\mathcal L$
. Thus, any such homomorphism equals
$\mathcal L$
. Thus, any such homomorphism equals
![]() $\operatorname {id}_{\mathcal L^+}$
. Similarly, any homomorphism of partial groups
$\operatorname {id}_{\mathcal L^+}$
. Similarly, any homomorphism of partial groups
![]() ${\widetilde {\mathcal {L}}}^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
that restricts to the identity on
${\widetilde {\mathcal {L}}}^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
that restricts to the identity on
![]() ${\widetilde {\mathcal {L}}}$
equals
${\widetilde {\mathcal {L}}}$
equals
![]() $\operatorname {id}_{{\widetilde {\mathcal {L}}}^+}$
. This shows
$\operatorname {id}_{{\widetilde {\mathcal {L}}}^+}$
. This shows
![]() $\gamma \hat {\gamma }=\operatorname {id}_{\mathcal L^+}$
and
$\gamma \hat {\gamma }=\operatorname {id}_{\mathcal L^+}$
and
![]() $\hat {\gamma }\gamma =\operatorname {id}_{{\widetilde {\mathcal {L}}}^+}$
; that is,
$\hat {\gamma }\gamma =\operatorname {id}_{{\widetilde {\mathcal {L}}}^+}$
; that is,
![]() $\gamma $
is bijective with inverse map
$\gamma $
is bijective with inverse map
![]() $\hat {\gamma }$
. So
$\hat {\gamma }$
. So
 $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
is an isomorphism of partial groups by Lemma 2.18. Because
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
is an isomorphism of partial groups by Lemma 2.18. Because
![]() $\Delta ^+\gamma =\Delta ^+\alpha =\widetilde {\Delta }^+$
and
$\Delta ^+\gamma =\Delta ^+\alpha =\widetilde {\Delta }^+$
and
![]() $\Delta \gamma =\Delta \alpha =\widetilde {\Delta }$
, it follows that
$\Delta \gamma =\Delta \alpha =\widetilde {\Delta }$
, it follows that
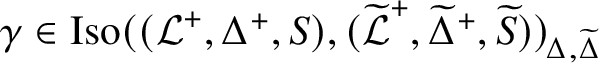 $\gamma \in \mathrm {Iso}((\mathcal L^+,\Delta ^+,S),({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}}))_{\Delta ,\widetilde {\Delta }}$
with
$\gamma \in \mathrm {Iso}((\mathcal L^+,\Delta ^+,S),({\widetilde {\mathcal {L}}}^+,\widetilde {\Delta }^+,{\widetilde {S}}))_{\Delta ,\widetilde {\Delta }}$
with
![]() $\Psi (\gamma )=\gamma |_{\mathcal L}=\alpha $
. This shows that
$\Psi (\gamma )=\gamma |_{\mathcal L}=\alpha $
. This shows that
![]() $\Psi $
is surjective. Because
$\Psi $
is surjective. Because
![]() $\gamma $
is the unique homomorphism of partial groups
$\gamma $
is the unique homomorphism of partial groups
![]() $\mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
that restricts to
$\mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}^+$
that restricts to
![]() $\alpha $
, the map
$\alpha $
, the map
![]() $\Psi $
is also injective.
$\Psi $
is also injective.
Theorem 5.2 Linking system version
Suppose that
![]() $\mathcal {T}$
,
$\mathcal {T}$
,
![]() $\mathcal {T}^{\;+}$
,
$\mathcal {T}^{\;+}$
,
![]() ${\widetilde {\mathcal {T}}}$
and
${\widetilde {\mathcal {T}}}$
and
![]() ${\widetilde {\mathcal {T}}}^{\;+}$
are linking systems and
${\widetilde {\mathcal {T}}}^{\;+}$
are linking systems and
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() ${\widetilde {\mathcal {F}}}$
are saturated fusion systems such that
${\widetilde {\mathcal {F}}}$
are saturated fusion systems such that
-
•
 $\mathcal {T}$
and
$\mathcal {T}$
and
 $\mathcal {T}^{\;+}$
are linking systems associated to
$\mathcal {T}^{\;+}$
are linking systems associated to
 $\mathcal {F}$
,
$\mathcal {F}$
,
 $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
,
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
,
 $\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
;
$\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
; -
•
 ${\widetilde {\mathcal {T}}}$
and
${\widetilde {\mathcal {T}}}$
and
 ${\widetilde {\mathcal {T}}}^{\;+}$
are linking systems associated to
${\widetilde {\mathcal {T}}}^{\;+}$
are linking systems associated to
 ${\widetilde {\mathcal {F}}}$
,
${\widetilde {\mathcal {F}}}$
,
 $\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}^{\;+})$
,
$\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)\subseteq \mathrm {Ob}({\widetilde {\mathcal {T}}}^{\;+})$
,
 ${\widetilde {\mathcal {T}}}={\widetilde {\mathcal {T}}}^{\;+}|_{\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)}$
.
${\widetilde {\mathcal {T}}}={\widetilde {\mathcal {T}}}^{\;+}|_{\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)}$
.
Then the map
 $$ \begin{align*}\mathrm{Iso}(\mathcal{T}^{\;+},{\widetilde{\mathcal{T}}}^{\;+})_{\mathrm{Ob}(\mathcal{T}\;),\mathrm{Ob}({\widetilde{\mathcal{T}}}\;)}\longrightarrow \mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}}\;)_{\mathrm{Ob}(\mathcal{T}^{\;+}),\mathrm{Ob}({\widetilde{\mathcal{T}}}^{\;+})},\;\alpha\mapsto\alpha|_{\mathcal{T}}\end{align*} $$
$$ \begin{align*}\mathrm{Iso}(\mathcal{T}^{\;+},{\widetilde{\mathcal{T}}}^{\;+})_{\mathrm{Ob}(\mathcal{T}\;),\mathrm{Ob}({\widetilde{\mathcal{T}}}\;)}\longrightarrow \mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}}\;)_{\mathrm{Ob}(\mathcal{T}^{\;+}),\mathrm{Ob}({\widetilde{\mathcal{T}}}^{\;+})},\;\alpha\mapsto\alpha|_{\mathcal{T}}\end{align*} $$
is a bijection.
Proof. Because we are dealing with transporter systems, in this proof we will again write functions from the left. Set
![]() $\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
,
$\Delta :=\mathrm {Ob}(\mathcal {T}\;)$
,
![]() $\Delta ^+:=\mathrm {Ob}(\mathcal {T}^{\;+})$
,
$\Delta ^+:=\mathrm {Ob}(\mathcal {T}^{\;+})$
,
![]() $\widetilde {\Delta }:=\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
and
$\widetilde {\Delta }:=\mathrm {Ob}({\widetilde {\mathcal {T}}}\;)$
and
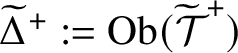 $\widetilde {\Delta }^+:=\mathrm {Ob}({\widetilde {\mathcal {T}}}^{\;+})$
,
$\widetilde {\Delta }^+:=\mathrm {Ob}({\widetilde {\mathcal {T}}}^{\;+})$
,
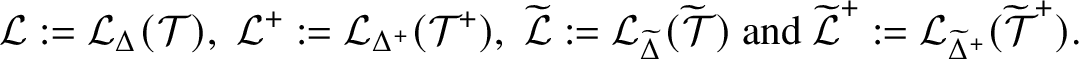 $$ \begin{align*}\mathcal L:=\mathcal L_\Delta(\mathcal{T}\;),\;\mathcal L^+:=\mathcal L_{\Delta^+}(\mathcal{T}^{\;+}),\;{\widetilde{\mathcal{L}}}:=\mathcal L_{\widetilde{\Delta}}({\widetilde{\mathcal{T}}}\;)\mbox{ and }{\widetilde{\mathcal{L}}}^+:=\mathcal L_{\widetilde{\Delta}^+}({\widetilde{\mathcal{T}}}^{\;+}).\end{align*} $$
$$ \begin{align*}\mathcal L:=\mathcal L_\Delta(\mathcal{T}\;),\;\mathcal L^+:=\mathcal L_{\Delta^+}(\mathcal{T}^{\;+}),\;{\widetilde{\mathcal{L}}}:=\mathcal L_{\widetilde{\Delta}}({\widetilde{\mathcal{T}}}\;)\mbox{ and }{\widetilde{\mathcal{L}}}^+:=\mathcal L_{\widetilde{\Delta}^+}({\widetilde{\mathcal{T}}}^{\;+}).\end{align*} $$
By
![]() $[\varphi ]$
we denote the equivalence class of
$[\varphi ]$
we denote the equivalence class of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal L$
if
$\mathcal L$
if
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and the equivalence class of
$\varphi \in \mathrm {Iso}(\mathcal {T}\;)$
and the equivalence class of
![]() $\varphi $
in
$\varphi $
in
![]() ${\widetilde {\mathcal {L}}}$
if
${\widetilde {\mathcal {L}}}$
if
![]() $\varphi \in \mathrm {Iso}({\widetilde {\mathcal {T}}}\;)$
. Similarly,
$\varphi \in \mathrm {Iso}({\widetilde {\mathcal {T}}}\;)$
. Similarly,
![]() $[\varphi ]_+$
denotes the equivalence class of
$[\varphi ]_+$
denotes the equivalence class of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal L^+$
if
$\mathcal L^+$
if
![]() $\varphi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
and the equivalence class of
$\varphi \in \mathrm {Iso}(\mathcal {T}^{\;+})$
and the equivalence class of
![]() $\varphi $
in
$\varphi $
in
![]() ${\widetilde {\mathcal {L}}}^+$
if
${\widetilde {\mathcal {L}}}^+$
if
 $\varphi \in \mathrm {Iso}({\widetilde {\mathcal {T}}}^{\;+})$
. By Lemma 4.5, the maps
$\varphi \in \mathrm {Iso}({\widetilde {\mathcal {T}}}^{\;+})$
. By Lemma 4.5, the maps
![]() $\iota \colon \mathcal L\longrightarrow \mathcal L^+|_\Delta ,[\varphi ]\mapsto [\varphi ]_+$
and
$\iota \colon \mathcal L\longrightarrow \mathcal L^+|_\Delta ,[\varphi ]\mapsto [\varphi ]_+$
and
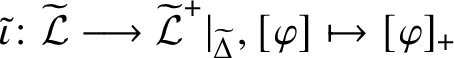 ${\tilde {\iota }}\colon {\widetilde {\mathcal {L}}}\longrightarrow {\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},[\varphi ]\mapsto [\varphi ]_+$
are isomorphisms of localities that restrict to the identity on S. In particular, the map
${\tilde {\iota }}\colon {\widetilde {\mathcal {L}}}\longrightarrow {\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},[\varphi ]\mapsto [\varphi ]_+$
are isomorphisms of localities that restrict to the identity on S. In particular, the map
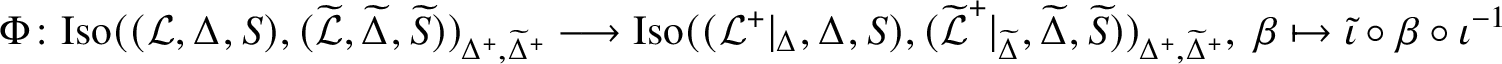 $$ \begin{align*}\Phi\colon \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\longrightarrow \mathrm{Iso}((\mathcal L^+|_\Delta,\Delta,S),({\widetilde{\mathcal{L}}}^+|_{\widetilde{\Delta}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+},\;\beta\mapsto {\tilde{\iota}}\circ\beta\circ \iota^{-1}\end{align*} $$
$$ \begin{align*}\Phi\colon \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\longrightarrow \mathrm{Iso}((\mathcal L^+|_\Delta,\Delta,S),({\widetilde{\mathcal{L}}}^+|_{\widetilde{\Delta}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+},\;\beta\mapsto {\tilde{\iota}}\circ\beta\circ \iota^{-1}\end{align*} $$
is a bijection. By Lemma 2.24, there is also a bijection
 $$ \begin{align*}\Psi\colon \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L^+|_\Delta,\Delta,S),({\widetilde{\mathcal{L}}}^+|_{\widetilde{\Delta}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
$$ \begin{align*}\Psi\colon \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L^+|_\Delta,\Delta,S),({\widetilde{\mathcal{L}}}^+|_{\widetilde{\Delta}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
given by restriction. Moreover, by Lemma 4.6, there are bijections
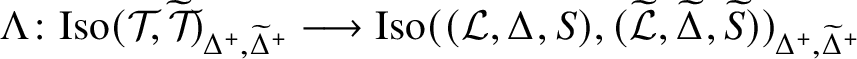 $$ \begin{align*}\Lambda\colon \mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}})_{\Delta^+,\widetilde{\Delta}^+}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
$$ \begin{align*}\Lambda\colon \mathrm{Iso}(\mathcal{T},{\widetilde{\mathcal{T}}})_{\Delta^+,\widetilde{\Delta}^+}\longrightarrow \mathrm{Iso}((\mathcal L,\Delta,S),({\widetilde{\mathcal{L}}},\widetilde{\Delta},{\widetilde{S}}))_{\Delta^+,\widetilde{\Delta}^+}\end{align*} $$
and
 $$ \begin{align*}\Lambda^+\colon \mathrm{Iso}(\mathcal{T}^{\;+},{\widetilde{\mathcal{T}}}^{\;+})_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}.\end{align*} $$
$$ \begin{align*}\Lambda^+\colon \mathrm{Iso}(\mathcal{T}^{\;+},{\widetilde{\mathcal{T}}}^{\;+})_{\Delta,\widetilde{\Delta}}\longrightarrow \mathrm{Iso}((\mathcal L^+,\Delta^+,S),({\widetilde{\mathcal{L}}}^+,\widetilde{\Delta}^+,{\widetilde{S}}))_{\Delta,\widetilde{\Delta}}.\end{align*} $$
Here
![]() $\Lambda $
is defined by
$\Lambda $
is defined by
for all
 $\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
, all
$\alpha \in \mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
, all
![]() $P,Q\in \Delta $
and all
$P,Q\in \Delta $
and all
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
, and
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
, and
![]() $\Lambda ^+$
is defined by
$\Lambda ^+$
is defined by
for all
 $\alpha \in \mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
, all
$\alpha \in \mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
, all
![]() $P,Q\in \Delta ^+$
and all
$P,Q\in \Delta ^+$
and all
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}^{\;+}}(P,Q)$
.
$\varphi \in \mathrm {Iso}_{\mathcal {T}^{\;+}}(P,Q)$
.
Now
![]() $\Psi \circ \Lambda ^+$
is a bijection from
$\Psi \circ \Lambda ^+$
is a bijection from
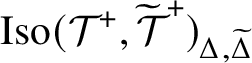 $\mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
to
$\mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
to
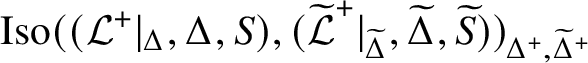 $\mathrm {Iso}((\mathcal L^+|_\Delta ,\Delta ,S),({\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
and
$\mathrm {Iso}((\mathcal L^+|_\Delta ,\Delta ,S),({\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
and
![]() $\Phi \circ \Lambda $
is a bijection from
$\Phi \circ \Lambda $
is a bijection from
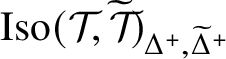 $\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
to
$\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
to
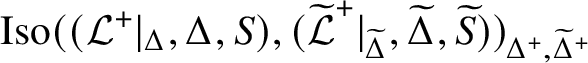 $\mathrm {Iso}((\mathcal L^+|_\Delta ,\Delta ,S),({\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
. Hence,
$\mathrm {Iso}((\mathcal L^+|_\Delta ,\Delta ,S),({\widetilde {\mathcal {L}}}^+|_{\widetilde {\Delta }},\widetilde {\Delta },{\widetilde {S}}))_{\Delta ^+,\widetilde {\Delta }^+}$
. Hence,
![]() $\Theta :=(\Phi \circ \Lambda )^{-1}\circ (\Psi \circ \Lambda ^+)$
is a bijection from
$\Theta :=(\Phi \circ \Lambda )^{-1}\circ (\Psi \circ \Lambda ^+)$
is a bijection from
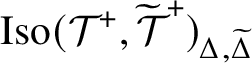 $\mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
to
$\mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
to
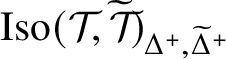 $\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
. Fixing
$\mathrm {Iso}(\mathcal {T},{\widetilde {\mathcal {T}}})_{\Delta ^+,\widetilde {\Delta }^+}$
. Fixing
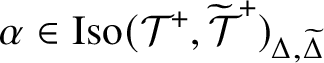 $\alpha \in \mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
, it only remains to show that
$\alpha \in \mathrm {Iso}(\mathcal {T}^{\;+},{\widetilde {\mathcal {T}}}^{\;+})_{\Delta ,\widetilde {\Delta }}$
, it only remains to show that
![]() $\Theta (\alpha )=\alpha |_{\mathcal {T}}$
or, equivalently,
$\Theta (\alpha )=\alpha |_{\mathcal {T}}$
or, equivalently,
![]() $\Psi (\Lambda ^+(\alpha ))=\Phi (\Lambda (\alpha |_{\mathcal {T}}))$
. To prove the latter equality, recall that
$\Psi (\Lambda ^+(\alpha ))=\Phi (\Lambda (\alpha |_{\mathcal {T}}))$
. To prove the latter equality, recall that
![]() $\iota \colon \mathcal L\longrightarrow \mathcal L^+|_\Delta $
is bijective. So every element of
$\iota \colon \mathcal L\longrightarrow \mathcal L^+|_\Delta $
is bijective. So every element of
![]() $\mathcal L^+|_\Delta $
is of the form
$\mathcal L^+|_\Delta $
is of the form
![]() $\iota ([\varphi ])=[\varphi ]_+$
for some
$\iota ([\varphi ])=[\varphi ]_+$
for some
![]() $P,Q\in \Delta $
and
$P,Q\in \Delta $
and
![]() $\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
. We then compute
$\varphi \in \mathrm {Iso}_{\mathcal {T}}(P,Q)$
. We then compute
and
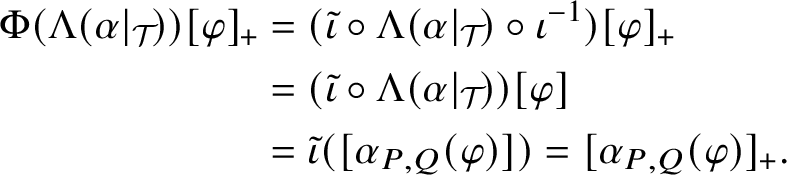 $$ \begin{align*} \Phi(\Lambda(\alpha|_{\mathcal{T}}))[\varphi]_+ &= ({\tilde{\iota}}\circ\Lambda(\alpha|_{\mathcal{T}})\circ \iota^{-1})[\varphi]_+\\ &= ({\tilde{\iota}}\circ\Lambda(\alpha|_{\mathcal{T}}))[\varphi]\\ &={\tilde{\iota}}([\alpha_{P,Q}(\varphi)])=[\alpha_{P,Q}(\varphi)]_+. \end{align*} $$
$$ \begin{align*} \Phi(\Lambda(\alpha|_{\mathcal{T}}))[\varphi]_+ &= ({\tilde{\iota}}\circ\Lambda(\alpha|_{\mathcal{T}})\circ \iota^{-1})[\varphi]_+\\ &= ({\tilde{\iota}}\circ\Lambda(\alpha|_{\mathcal{T}}))[\varphi]\\ &={\tilde{\iota}}([\alpha_{P,Q}(\varphi)])=[\alpha_{P,Q}(\varphi)]_+. \end{align*} $$
This proves the assertion.
The two preceding theorems seem most important in situations where we consider automorphisms of linking localities or linking systems. In the next two theorems we state the results for automorphisms explicitly.
Theorem 5.3 Linking locality version
Let
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
. Then the map
$\mathcal L=\mathcal L^+|_\Delta $
. Then the map
is well defined and an isomorphism of groups. In particular, if
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^+$
are
$\Delta ^+$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then the map
$\mathrm {Aut}(\mathcal {F})$
-invariant, then the map
![]() $\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)\longrightarrow \mathrm {Aut}(\mathcal L,\Delta ,S),\;\gamma \mapsto \gamma |_{\mathcal L}$
is an isomorphism of groups.
$\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)\longrightarrow \mathrm {Aut}(\mathcal L,\Delta ,S),\;\gamma \mapsto \gamma |_{\mathcal L}$
is an isomorphism of groups.
Proof. By Theorem 5.1, the map
![]() $\Psi $
is well defined and a bijection. Moreover, if
$\Psi $
is well defined and a bijection. Moreover, if
![]() $\beta ,\gamma \in \mathrm {Aut}(\mathcal L^+,\Delta ^+,S)_\Delta $
, then
$\beta ,\gamma \in \mathrm {Aut}(\mathcal L^+,\Delta ^+,S)_\Delta $
, then
![]() $\Psi (\beta \gamma )=(\beta \gamma )|_{\mathcal L}=(\beta |_{\mathcal L})(\gamma |_{\mathcal L})=\Psi (\beta )\Psi (\gamma )$
. Hence,
$\Psi (\beta \gamma )=(\beta \gamma )|_{\mathcal L}=(\beta |_{\mathcal L})(\gamma |_{\mathcal L})=\Psi (\beta )\Psi (\gamma )$
. Hence,
![]() $\Psi $
is an isomorphism of groups. By Lemma 2.21, if
$\Psi $
is an isomorphism of groups. By Lemma 2.21, if
![]() $\alpha $
is an element of
$\alpha $
is an element of
![]() $\mathrm {Aut}(\mathcal L,\Delta ,S)$
or of
$\mathrm {Aut}(\mathcal L,\Delta ,S)$
or of
![]() $\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
, then
$\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
, then
![]() $\alpha |_S\in \mathrm {Aut}(\mathcal {F})$
. Hence, if
$\alpha |_S\in \mathrm {Aut}(\mathcal {F})$
. Hence, if
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^+$
are
$\Delta ^+$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then
$\mathrm {Aut}(\mathcal {F})$
-invariant, then
![]() $\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)_\Delta =\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
and
$\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)_\Delta =\mathrm {Aut}(\mathcal L^+,\Delta ^+,S)$
and
![]() $\mathrm {Aut}(\mathcal L,\Delta ,S)_{\Delta ^+}=\mathrm {Aut}(\mathcal L,\Delta ,S)$
. This yields the assertion.
$\mathrm {Aut}(\mathcal L,\Delta ,S)_{\Delta ^+}=\mathrm {Aut}(\mathcal L,\Delta ,S)$
. This yields the assertion.
Theorem 5.4 Linking system version
Let
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
be linking systems associated to the same fusion system
$\mathcal {T}^{\;+}$
be linking systems associated to the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
![]() $\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
. Then the map
$\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
. Then the map
is an isomorphism of groups. In particular, if
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then the map
$\mathrm {Aut}(\mathcal {F})$
-invariant, then the map
![]() $\mathrm {Aut}(\mathcal {T}^{\;+})\longrightarrow \mathrm {Aut}(\mathcal {T}\;),\;\alpha \mapsto \alpha |_{\mathcal {T}}$
is an isomorphism of groups.
$\mathrm {Aut}(\mathcal {T}^{\;+})\longrightarrow \mathrm {Aut}(\mathcal {T}\;),\;\alpha \mapsto \alpha |_{\mathcal {T}}$
is an isomorphism of groups.
Proof. By Theorem 5.2,
![]() $\Theta $
is a bijection, and it is easy to to see that
$\Theta $
is a bijection, and it is easy to to see that
![]() $\Theta $
is an isomorphism of groups. As explained in Remark 4.2(b), if
$\Theta $
is an isomorphism of groups. As explained in Remark 4.2(b), if
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then
$\mathrm {Aut}(\mathcal {F})$
-invariant, then
![]() $\mathrm {Aut}(\mathcal {T}\;)_{\mathrm {Ob}(\mathcal {T}^{\;+})}=\mathrm {Aut}(\mathcal {T}\;)$
and
$\mathrm {Aut}(\mathcal {T}\;)_{\mathrm {Ob}(\mathcal {T}^{\;+})}=\mathrm {Aut}(\mathcal {T}\;)$
and
![]() $\mathrm {Aut}(\mathcal {T}^{\;+})_{\mathrm {Ob}(\mathcal {T}\;)}=\mathrm {Aut}(\mathcal {T}^{\;+})$
.
$\mathrm {Aut}(\mathcal {T}^{\;+})_{\mathrm {Ob}(\mathcal {T}\;)}=\mathrm {Aut}(\mathcal {T}^{\;+})$
.
Proof of Theorem A.1
Let
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta ^+$
are
$\Delta ^+$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant. By [Reference Henke14, Theorem A(b)], there exists a subcentric linking locality
$\mathrm {Aut}(\mathcal {F})$
-invariant. By [Reference Henke14, Theorem A(b)], there exists a subcentric linking locality
![]() $(\mathcal L^s,\mathcal {F}^s,S)$
over
$(\mathcal L^s,\mathcal {F}^s,S)$
over
![]() $\mathcal {F}$
. Because
$\mathcal {F}$
. Because
![]() $\mathcal {F}^{cr}\subseteq \Delta $
and
$\mathcal {F}^{cr}\subseteq \Delta $
and
![]() $\mathcal {F}^{cr}\subseteq \Delta ^+$
, it follows that
$\mathcal {F}^{cr}\subseteq \Delta ^+$
, it follows that
![]() $(\mathcal L^s|_\Delta ,\Delta ,S)$
and
$(\mathcal L^s|_\Delta ,\Delta ,S)$
and
![]() $(\mathcal L^s|_{\Delta ^+},\Delta ^+,S)$
are linking localities over
$(\mathcal L^s|_{\Delta ^+},\Delta ^+,S)$
are linking localities over
![]() $\mathcal {F}$
. Hence, by [Reference Henke14, Theorem A(a)], there exist rigid isomorphisms from
$\mathcal {F}$
. Hence, by [Reference Henke14, Theorem A(a)], there exist rigid isomorphisms from
![]() $(\mathcal L^s|_\Delta ,\Delta ,S)$
to
$(\mathcal L^s|_\Delta ,\Delta ,S)$
to
![]() $(\mathcal L,\Delta ,S)$
and from
$(\mathcal L,\Delta ,S)$
and from
![]() $(\mathcal L^s|_{\Delta ^+},\Delta ^+,S)$
to
$(\mathcal L^s|_{\Delta ^+},\Delta ^+,S)$
to
![]() $(\mathcal L^+,\Delta ^+,S)$
. By [Reference Henke14, Lemma 3.6],
$(\mathcal L^+,\Delta ^+,S)$
. By [Reference Henke14, Lemma 3.6],
![]() $\mathcal {F}^s$
is
$\mathcal {F}^s$
is
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant. Hence, applying Theorem 5.3 twice, we obtain
$\mathrm {Aut}(\mathcal {F})$
-invariant. Hence, applying Theorem 5.3 twice, we obtain
We will prove Theorem A.2 together with the following similar statement about outer automorphism groups, which is a generalization of [Reference Andersen, Oliver and Ventura2, Lemma 1.17].
Theorem 5.5. If
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
are linking systems associated to
$\mathcal {T}^{\;+}$
are linking systems associated to
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then
$\mathrm {Aut}(\mathcal {F})$
-invariant, then
If
![]() $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
![]() $\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then an isomorphism
$\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then an isomorphism
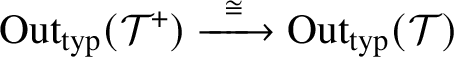 $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\xrightarrow {\;\;\cong \;\;}\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is given by sending the class of
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\xrightarrow {\;\;\cong \;\;}\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
is given by sending the class of
![]() $\alpha \in \mathrm {Aut}(\mathcal {T}^{\;+})$
to the class of
$\alpha \in \mathrm {Aut}(\mathcal {T}^{\;+})$
to the class of
![]() $\alpha |_{\mathcal {T}}\in \mathrm {Aut}(\mathcal {T}\;)$
.
$\alpha |_{\mathcal {T}}\in \mathrm {Aut}(\mathcal {T}\;)$
.
Proof of Theorem A.2 and Theorem 5.5
Let
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
be transporter systems over the same fusion system
$\mathcal {T}^{\;+}$
be transporter systems over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant. As usual when dealing with transporter systems, we write maps on the left side of the argument.
$\mathrm {Aut}(\mathcal {F})$
-invariant. As usual when dealing with transporter systems, we write maps on the left side of the argument.
If
![]() $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
![]() $\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then by Theorem 5.4, the map
$\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then by Theorem 5.4, the map
![]() $\mathrm {Aut}(\mathcal {T}^{\;+})\rightarrow \mathrm {Aut}(\mathcal {T}\;),\gamma \mapsto \gamma |_{\mathcal {T}}$
is a group isomorphism. Because
$\mathrm {Aut}(\mathcal {T}^{\;+})\rightarrow \mathrm {Aut}(\mathcal {T}\;),\gamma \mapsto \gamma |_{\mathcal {T}}$
is a group isomorphism. Because
![]() $\mathrm {Aut}_{\mathcal {T}}(S)=\mathrm {Aut}_{\mathcal {T}^{\;+}}(S)$
, one easily observes that it induces an isomorphism between the group of inner automorphisms of
$\mathrm {Aut}_{\mathcal {T}}(S)=\mathrm {Aut}_{\mathcal {T}^{\;+}}(S)$
, one easily observes that it induces an isomorphism between the group of inner automorphisms of
![]() $\mathcal {T}^{\;+}$
and the group of inner automorphisms of
$\mathcal {T}^{\;+}$
and the group of inner automorphisms of
![]() $\mathcal {T}$
. Hence, by Lemma 4.10, it induces an isomorphism
$\mathcal {T}$
. Hence, by Lemma 4.10, it induces an isomorphism
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\rightarrow \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
that takes the class of
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\rightarrow \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)$
that takes the class of
![]() $\alpha \in \mathrm {Aut}(\mathcal {T}^{\;+})$
to the class of
$\alpha \in \mathrm {Aut}(\mathcal {T}^{\;+})$
to the class of
![]() $\alpha |_{\mathcal {T}}$
.
$\alpha |_{\mathcal {T}}$
.
Suppose now that
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
are arbitrary. By [Reference Henke14, Theorem A], there exists a subcentric linking system
$\mathcal {T}^{\;+}$
are arbitrary. By [Reference Henke14, Theorem A], there exists a subcentric linking system
![]() $\mathcal {T}^{\;s}$
over
$\mathcal {T}^{\;s}$
over
![]() $\mathcal {F}$
; moreover,
$\mathcal {F}$
; moreover,
![]() $\mathcal {T}$
is rigidly isomorphic to
$\mathcal {T}$
is rigidly isomorphic to
![]() $\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, and
$\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, and
![]() $\mathcal {T}^{\;+}$
is rigidly isomorphic to
$\mathcal {T}^{\;+}$
is rigidly isomorphic to
![]() $\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})}$
. If
$\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})}$
. If
![]() $\alpha \colon \mathcal {T}\rightarrow \mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
is a rigid isomorphism, then the map
$\alpha \colon \mathcal {T}\rightarrow \mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
is a rigid isomorphism, then the map
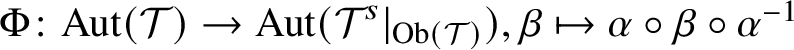 $\Phi \colon \mathrm {Aut}(\mathcal {T}\;)\rightarrow \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}),\beta \mapsto \alpha \circ \beta \circ \alpha ^{-1}$
is an isomorphism of groups and so
$\Phi \colon \mathrm {Aut}(\mathcal {T}\;)\rightarrow \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}),\beta \mapsto \alpha \circ \beta \circ \alpha ^{-1}$
is an isomorphism of groups and so
![]() $\mathrm {Aut}(\mathcal {T}\;)\cong \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)})$
. One can check now that, for any
$\mathrm {Aut}(\mathcal {T}\;)\cong \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)})$
. One can check now that, for any
![]() $\gamma \in \mathrm {Aut}(\mathcal {T}\;)$
, we have
$\gamma \in \mathrm {Aut}(\mathcal {T}\;)$
, we have
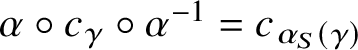 $\alpha \circ c_\gamma \circ \alpha ^{-1}=c_{\alpha _S(\gamma )}$
; to see that
$\alpha \circ c_\gamma \circ \alpha ^{-1}=c_{\alpha _S(\gamma )}$
; to see that
![]() $\alpha \circ c_\gamma \circ \alpha ^{-1}$
and
$\alpha \circ c_\gamma \circ \alpha ^{-1}$
and
![]() $c_{\alpha _S(\gamma )}$
agree on objects, one uses that
$c_{\alpha _S(\gamma )}$
agree on objects, one uses that
![]() ${\tilde {\pi }}\circ \alpha =\pi $
(cf. Remark 4.2(d)), and to see that the two functors agree on morphisms, one uses that
${\tilde {\pi }}\circ \alpha =\pi $
(cf. Remark 4.2(d)), and to see that the two functors agree on morphisms, one uses that
![]() $\alpha $
takes inclusions to inclusions and thus commutes with taking restrictions. So
$\alpha $
takes inclusions to inclusions and thus commutes with taking restrictions. So
![]() $\Phi $
induces an isomorphism between the group of inner automorphisms of
$\Phi $
induces an isomorphism between the group of inner automorphisms of
![]() $\mathcal {T}$
and the group of inner automorphisms of
$\mathcal {T}$
and the group of inner automorphisms of
![]() $\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
. Thus, by Lemma 4.10,
$\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}$
. Thus, by Lemma 4.10,
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)\cong \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)})$
. Similarly, one shows that
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}\;)\cong \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)})$
. Similarly, one shows that
![]() $\mathrm {Aut}(\mathcal {T}^{\;+})\cong \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})})$
and
$\mathrm {Aut}(\mathcal {T}^{\;+})\cong \mathrm {Aut}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})})$
and
![]() $\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\cong \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})})$
. So using Theorem 5.4 twice, we can conclude that
$\mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;+})\cong \mathrm {Out}_{\operatorname {typ}}(\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}^{\;+})})$
. So using Theorem 5.4 twice, we can conclude that
and, similarly,
Remark 5.6. Theorem A.2 and Theorem 5.5 were shown for linking systems whose objects are quasicentric in [Reference Andersen, Oliver and Ventura2, Lemma 1.17] and its proof via more direct arguments. As we will briefly indicate now, the proof could be adapted to give a proof of Theorems A.2 and 5.5 that does not use linking localities:
-
• Using the notation in the proof of [Reference Andersen, Oliver and Ventura2, Lemma 1.17], Lemma 4.9(b) is needed to conclude that P is properly contained in
 $\hat {P}$
. The reference to [Reference Andersen, Oliver and Ventura2, Theorem 1.12] needs to be replaced by a reference to Lemma 4.9(c).
$\hat {P}$
. The reference to [Reference Andersen, Oliver and Ventura2, Theorem 1.12] needs to be replaced by a reference to Lemma 4.9(c). -
• The references to Proposition 1.11(b),(b’) and Proposition 1.11(d) in Reference Andersen, Oliver and Ventura[2] need to be replaced by references to Lemma 3.2(c) and Proposition 3.4(a) in Reference Oliver and Ventura[21], respectively.
-
• References to [Reference Andersen, Oliver and Ventura2, Proposition 1.11(e)] could be replaced by references to Axiom II in the definition of a transporter system [Reference Oliver and Ventura21, Definition 3.1] and to [Reference Oliver and Ventura21, Lemma 3.3].
-
• The reference to [Reference Andersen, Oliver and Ventura2, Lemma 1.15] can be replaced by a reference to [Reference Glauberman and Lynd12, Proposition 2.5] (cf. Remark 4.2(d)).
It seems that the arguments could also be adapted to give direct proofs of the more general Theorems 5.2 and 5.4.
Proof of Theorem B. If
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {T}^{\;+}$
are linking systems associated to the same saturated fusion system
$\mathcal {T}^{\;+}$
are linking systems associated to the same saturated fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
$\mathrm {Ob}(\mathcal {T}\;)\subseteq \mathrm {Ob}(\mathcal {T}^{\;+})$
and
![]() $\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then by [Reference Henke14, Theorem A], the inclusion map
$\mathcal {T}=\mathcal {T}^{\;+}|_{\mathrm {Ob}(\mathcal {T}\;)}$
, then by [Reference Henke14, Theorem A], the inclusion map
![]() $\iota \colon \mathcal {T}\hookrightarrow \mathcal {T}^{\;+}$
induces a homotopy equivalence
$\iota \colon \mathcal {T}\hookrightarrow \mathcal {T}^{\;+}$
induces a homotopy equivalence
![]() $|\iota |\colon |\mathcal {T}\;|\rightarrow |\mathcal {T}^{\;+}|$
and thus a homotopy equivalence
$|\iota |\colon |\mathcal {T}\;|\rightarrow |\mathcal {T}^{\;+}|$
and thus a homotopy equivalence
 $|\iota |^\wedge _p\colon |\mathcal {T}\;|^\wedge _p\rightarrow |\mathcal {T}^{\;+}|^\wedge _p$
. Moreover, if
$|\iota |^\wedge _p\colon |\mathcal {T}\;|^\wedge _p\rightarrow |\mathcal {T}^{\;+}|^\wedge _p$
. Moreover, if
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant and
$\mathrm {Aut}(\mathcal {F})$
-invariant and
![]() $\gamma \in \mathrm {Aut}(\mathcal {T}^{\;+})$
, then the commutative square
$\gamma \in \mathrm {Aut}(\mathcal {T}^{\;+})$
, then the commutative square
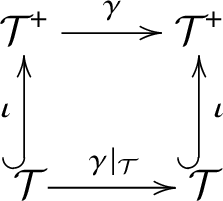
induces a commutative square after applying the functor
![]() $|\cdot |^\wedge _p$
. Thus, if
$|\cdot |^\wedge _p$
. Thus, if
![]() $\mathrm {Ob}(\mathcal {T}\;)$
and
$\mathrm {Ob}(\mathcal {T}\;)$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;+})$
are
$\mathrm {Ob}(\mathcal {T}^{\;+})$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant, then by Theorem 5.5, the conclusion of Corollary B is true for
$\mathrm {Aut}(\mathcal {F})$
-invariant, then by Theorem 5.5, the conclusion of Corollary B is true for
![]() $\mathcal {T}$
if and only if it is true with
$\mathcal {T}$
if and only if it is true with
![]() $\mathcal {T}^{\;+}$
in place of
$\mathcal {T}^{\;+}$
in place of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Suppose now that
![]() $\mathcal {T}$
is an arbitrary linking system associated to
$\mathcal {T}$
is an arbitrary linking system associated to
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathrm {Ob}(\mathcal {T}\;)$
is
$\mathrm {Ob}(\mathcal {T}\;)$
is
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant. By [Reference Henke14, Theorem A], there exists a subcentric linking system
$\mathrm {Aut}(\mathcal {F})$
-invariant. By [Reference Henke14, Theorem A], there exists a subcentric linking system
![]() $\mathcal {T}^{\;s}$
associated to
$\mathcal {T}^{\;s}$
associated to
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}=\mathcal {T}$
; moreover,
$\mathcal {T}^{\;s}|_{\mathrm {Ob}(\mathcal {T}\;)}=\mathcal {T}$
; moreover,
![]() $\mathcal {T}^{\;c}:=\mathcal {T}^{\;s}|_{\mathcal {F}^c}$
is a centric linking system associated to
$\mathcal {T}^{\;c}:=\mathcal {T}^{\;s}|_{\mathcal {F}^c}$
is a centric linking system associated to
![]() $\mathcal {F}$
. By [Reference Broto, Levi and Oliver3, Theorem 8.1] and its proof, the statement in Theorem B is true for
$\mathcal {F}$
. By [Reference Broto, Levi and Oliver3, Theorem 8.1] and its proof, the statement in Theorem B is true for
![]() $\mathcal {T}^{\;c}$
in place of
$\mathcal {T}^{\;c}$
in place of
![]() $\mathcal {T}$
. The object sets
$\mathcal {T}$
. The object sets
![]() $\mathrm {Ob}(\mathcal {T}^{\;c})=\mathcal {F}^c$
and
$\mathrm {Ob}(\mathcal {T}^{\;c})=\mathcal {F}^c$
and
![]() $\mathrm {Ob}(\mathcal {T}^{\;s})=\mathcal {F}^s$
are
$\mathrm {Ob}(\mathcal {T}^{\;s})=\mathcal {F}^s$
are
![]() $\mathrm {Aut}(\mathcal {F})$
-invariant (cf. [Reference Henke14, Lemma 3.6]). Hence, as remarked above, the conclusion of Theorem B is true for
$\mathrm {Aut}(\mathcal {F})$
-invariant (cf. [Reference Henke14, Lemma 3.6]). Hence, as remarked above, the conclusion of Theorem B is true for
![]() $\mathcal {T}^{\;s}$
and thus also for
$\mathcal {T}^{\;s}$
and thus also for
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
6. Partial normal subgroups
This section is mainly devoted to the proof of Theorem C. We will, however, start in the first subsection with some background on partial normal subgroups of localities. Most important, we prove with Lemma 6.2 a result that seems to be of general interest and can be considered as a version of Alperin’s fusion theorem for partial normal subgroups. This lemma is also applied in Reference Chermak and Henke[10]. Using Lemma 6.2 we will then prove Theorem C and a corollary in Subsection 6.2.
6.1. General results
If
![]() $\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups, then by [Reference Chermak7, Lemma 1.14],
$\alpha \colon \mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups, then by [Reference Chermak7, Lemma 1.14],
![]() $\ker (\alpha )$
is a partial normal subgroup of
$\ker (\alpha )$
is a partial normal subgroup of
![]() $\mathcal L$
. The other way around, if
$\mathcal L$
. The other way around, if
![]() $(\mathcal L,\Delta ,S)$
is a locality and
$(\mathcal L,\Delta ,S)$
is a locality and
![]() $\mathcal {N}$
is a partial normal subgroup of
$\mathcal {N}$
is a partial normal subgroup of
![]() $\mathcal L$
, then one can construct a partial group
$\mathcal L$
, then one can construct a partial group
![]() $\mathcal L/\mathcal {N}$
and a projection of partial groups
$\mathcal L/\mathcal {N}$
and a projection of partial groups
with
![]() $\ker (\alpha )=\mathcal {N}$
. We refer the reader to Lemma 3.16 and the preceding explanations in [Reference Chermak7, Section 3] for details of the construction. We will often adopt a ‘bar notation’ similarly as for groups. This means that, setting
$\ker (\alpha )=\mathcal {N}$
. We refer the reader to Lemma 3.16 and the preceding explanations in [Reference Chermak7, Section 3] for details of the construction. We will often adopt a ‘bar notation’ similarly as for groups. This means that, setting
![]() $\overline {\mathcal L}=\mathcal L/\mathcal {N}$
, for every element or subset X of
$\overline {\mathcal L}=\mathcal L/\mathcal {N}$
, for every element or subset X of
![]() $\mathcal L$
, we write
$\mathcal L$
, we write
![]() $\overline {X}$
for the image of X in
$\overline {X}$
for the image of X in
![]() $\overline {\mathcal L}$
under
$\overline {\mathcal L}$
under
![]() $\alpha $
. Moreover, for any set
$\alpha $
. Moreover, for any set
![]() $\Gamma $
of subgroups of
$\Gamma $
of subgroups of
![]() $\mathcal L$
, we set
$\mathcal L$
, we set
![]() $\overline {\Gamma }:=\{\overline {P}\colon P\in \Gamma \}$
. By [Reference Chermak7, Corollary 4.5],
$\overline {\Gamma }:=\{\overline {P}\colon P\in \Gamma \}$
. By [Reference Chermak7, Corollary 4.5],
![]() $(\overline {\mathcal L},\overline {\Delta },\overline {S})$
is a locality and
$(\overline {\mathcal L},\overline {\Delta },\overline {S})$
is a locality and
![]() $\alpha $
is a projection of localities from
$\alpha $
is a projection of localities from
![]() $(\mathcal L,\Delta ,S)$
to
$(\mathcal L,\Delta ,S)$
to
![]() $(\overline {\mathcal L},\overline {\Delta },\overline {S})$
.
$(\overline {\mathcal L},\overline {\Delta },\overline {S})$
.
Lemma 6.1. Let
![]() $(\mathcal L,\Delta ,S)$
be a locality with a partial normal subgroup
$(\mathcal L,\Delta ,S)$
be a locality with a partial normal subgroup
![]() $\mathcal {N}$
. Then the following hold:
$\mathcal {N}$
. Then the following hold:
-
(a) The triple
 $(\mathcal {N} S,\Delta ,S)$
is a locality.
$(\mathcal {N} S,\Delta ,S)$
is a locality. -
(b) For every
 $P\in \Delta $
,
$P\in \Delta $
,
 $O^p(N_{\mathcal {N} S}(P))=O^p(N_{\mathcal {N}}(P))$
.
$O^p(N_{\mathcal {N} S}(P))=O^p(N_{\mathcal {N}}(P))$
.
Proof. Part (a) is true by [Reference Chermak7, Lemma 4.1]. In particular,
![]() $N_{\mathcal {N} S}(P)$
is a subgroup of
$N_{\mathcal {N} S}(P)$
is a subgroup of
![]() $\mathcal L$
. Moreover, we may consider the canonical projection
$\mathcal L$
. Moreover, we may consider the canonical projection
![]() $\alpha \colon \mathcal {N} S\longrightarrow \overline {\mathcal {N} S}:=\mathcal {N} S/\mathcal {N}$
. Then
$\alpha \colon \mathcal {N} S\longrightarrow \overline {\mathcal {N} S}:=\mathcal {N} S/\mathcal {N}$
. Then
![]() $\overline {\mathcal {N} S}=\overline {S}$
is a p-group and
$\overline {\mathcal {N} S}=\overline {S}$
is a p-group and
![]() $\alpha $
induces a group homomorphism
$\alpha $
induces a group homomorphism
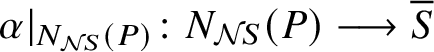 $\alpha |_{N_{\mathcal {N} S}(P)}\colon N_{\mathcal {N} S}(P)\longrightarrow \overline {S}$
. Thus,
$\alpha |_{N_{\mathcal {N} S}(P)}\colon N_{\mathcal {N} S}(P)\longrightarrow \overline {S}$
. Thus,
![]() $O^p(N_{\mathcal {N} S}(P))\leq \ker (\alpha |_{N_{\mathcal {N} S}(P)})=\ker (\alpha )\cap N_{\mathcal {N} S}(P)=N_{\mathcal {N}}(P)$
. This implies (b).
$O^p(N_{\mathcal {N} S}(P))\leq \ker (\alpha |_{N_{\mathcal {N} S}(P)})=\ker (\alpha )\cap N_{\mathcal {N} S}(P)=N_{\mathcal {N}}(P)$
. This implies (b).
For the next lemma recall that a subgroup H of a finite group G is called strongly p-embedded if
![]() $H\neq G$
, p divides
$H\neq G$
, p divides
![]() $|H|$
and
$|H|$
and
![]() $H\cap H^g$
is a
$H\cap H^g$
is a
![]() $p^\prime $
-group for all
$p^\prime $
-group for all
![]() $g\in G\backslash H$
.
$g\in G\backslash H$
.
Lemma 6.2. Let
![]() $(\mathcal L,\Delta ,S)$
be a locality. If
$(\mathcal L,\Delta ,S)$
be a locality. If
![]() $\mathcal {N}$
is a partial normal subgroup of
$\mathcal {N}$
is a partial normal subgroup of
![]() $\mathcal L$
and
$\mathcal L$
and
![]() $n\in \mathcal {N}$
, then there exist
$n\in \mathcal {N}$
, then there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $R_1,R_2,\dots ,R_k\in \Delta $
and
$R_1,R_2,\dots ,R_k\in \Delta $
and
![]() $(t,n_1,n_2,\dots ,n_k)\in \mathbf {D}$
such that the following hold:
$(t,n_1,n_2,\dots ,n_k)\in \mathbf {D}$
such that the following hold:
-
(i)
 $S_n=S_{(t,n_1,\dots ,n_k)}$
and
$S_n=S_{(t,n_1,\dots ,n_k)}$
and
 $n=tn_1n_2\cdots n_k$
;
$n=tn_1n_2\cdots n_k$
; -
(ii)
 $n_i\in O^p(N_{\mathcal {N}}(R_i))$
,
$n_i\in O^p(N_{\mathcal {N}}(R_i))$
,
 $S_{n_i}=R_i$
,
$S_{n_i}=R_i$
,
 $O_p(N_{\mathcal {N} S}(R_i))=R_i$
and
$O_p(N_{\mathcal {N} S}(R_i))=R_i$
and
 $N_S(R_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(R_i))$
for all
$N_S(R_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(R_i))$
for all
 $i=1,\dots ,k$
; and
$i=1,\dots ,k$
; and -
(iii)
 $t\in \mathcal {N}\cap S$
.
$t\in \mathcal {N}\cap S$
.
In fact,
![]() $R_1,\dots ,R_k$
can be chosen such that
$R_1,\dots ,R_k$
can be chosen such that
![]() $N_{\mathcal {N} S}(R_i)/R_i$
has a strongly p-embedded subgroup for all
$N_{\mathcal {N} S}(R_i)/R_i$
has a strongly p-embedded subgroup for all
![]() $i=1,\dots ,k$
.
$i=1,\dots ,k$
.
Proof. By Lemma 6.1(a),
![]() $(\mathcal {N} S,\Delta ,S)$
is a locality. So by Alperin’s fusion theorem for localities [Reference Molinier16, Theorem 2.5], there exist
$(\mathcal {N} S,\Delta ,S)$
is a locality. So by Alperin’s fusion theorem for localities [Reference Molinier16, Theorem 2.5], there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $Q_1,Q_2,\dots ,Q_k\in \Delta $
and
$Q_1,Q_2,\dots ,Q_k\in \Delta $
and
![]() $(g_1,g_2,\dots ,g_k)\in \mathbf {D}$
such that the following hold:
$(g_1,g_2,\dots ,g_k)\in \mathbf {D}$
such that the following hold:
-
•
 $S_n=S_{(g_1,\dots ,g_k)}$
and
$S_n=S_{(g_1,\dots ,g_k)}$
and
 $n=g_1g_2\cdots g_k$
;
$n=g_1g_2\cdots g_k$
; -
•
 $g_i\in N_{\mathcal {N} S}(Q_i)$
,
$g_i\in N_{\mathcal {N} S}(Q_i)$
,
 $S_{g_i}=Q_i$
,
$S_{g_i}=Q_i$
,
 $N_{\mathcal {N} S}(Q_i)/Q_i$
has a strongly p-embedded subgroup; and
$N_{\mathcal {N} S}(Q_i)/Q_i$
has a strongly p-embedded subgroup; and
 $N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
for all
$N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
for all
 $i=1,\dots ,k$
.
$i=1,\dots ,k$
.
Because
![]() $N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
, it follows from Lemma 6.1(b) that
$N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
, it follows from Lemma 6.1(b) that
![]() $N_{\mathcal {N} S}(Q_i)=N_S(Q_i)O^p(N_{\mathcal {N}}(Q_i))$
. So for all
$N_{\mathcal {N} S}(Q_i)=N_S(Q_i)O^p(N_{\mathcal {N}}(Q_i))$
. So for all
![]() $i=1,\dots ,n$
, we can write
$i=1,\dots ,n$
, we can write
![]() $g_i=s_im_i$
with
$g_i=s_im_i$
with
![]() $s_i\in N_S(Q_i)$
and
$s_i\in N_S(Q_i)$
and
![]() $m_i\in O^p(N_{\mathcal {N}}(Q_i))$
. By Lemma 2.8, we have
$m_i\in O^p(N_{\mathcal {N}}(Q_i))$
. By Lemma 2.8, we have
![]() $Q_i=S_{g_i}=S_{(s_i,m_i)}$
for all
$Q_i=S_{g_i}=S_{(s_i,m_i)}$
for all
![]() $i=1,\dots ,k$
. In particular,
$i=1,\dots ,k$
. In particular,
![]() $S_n=S_{(g_1,g_2,\dots ,g_k)}=S_{(s_1,m_1,s_2,m_2,\dots ,s_k,m_k)}$
and
$S_n=S_{(g_1,g_2,\dots ,g_k)}=S_{(s_1,m_1,s_2,m_2,\dots ,s_k,m_k)}$
and
Note also that
![]() $n=\Pi (g_1,\dots ,g_n)=\Pi (w)$
. Set
$n=\Pi (g_1,\dots ,g_n)=\Pi (w)$
. Set
Notice that
 $$ \begin{align*}x_ix_{i+1}^{-1}=s_i\mbox{ for }1\leq i<k\mbox{ and }x_k=s_k.\end{align*} $$
$$ \begin{align*}x_ix_{i+1}^{-1}=s_i\mbox{ for }1\leq i<k\mbox{ and }x_k=s_k.\end{align*} $$
Because
![]() $w\in \mathbf {D}$
via
$w\in \mathbf {D}$
via
![]() $S_n$
, it follows that
$S_n$
, it follows that
 $$ \begin{align*}v:=(x_1,x_2^{-1},m_1,x_2,x_3^{-1},m_2,x_3,\dots,x_k^{-1},m_{k-1},x_k,m_k)\in\mathbf{D}\mbox{ via }S_n\end{align*} $$
$$ \begin{align*}v:=(x_1,x_2^{-1},m_1,x_2,x_3^{-1},m_2,x_3,\dots,x_k^{-1},m_{k-1},x_k,m_k)\in\mathbf{D}\mbox{ via }S_n\end{align*} $$
and so, setting
![]() $t:=x_1$
, also
$t:=x_1$
, also
Observe, moreover, that, by axiom (PG3), we have
Using Lemma 2.7(f), it follows that
![]() $S_n=S_u$
. So (i) holds. Set
$S_n=S_u$
. So (i) holds. Set
Recall that
![]() $m_i\in O^p(N_{\mathcal {N}}(Q_i))$
,
$m_i\in O^p(N_{\mathcal {N}}(Q_i))$
,
![]() $N_{\mathcal {N} S}(Q_i)/Q_i$
has a strongly p-embedded subgroup and
$N_{\mathcal {N} S}(Q_i)/Q_i$
has a strongly p-embedded subgroup and
![]() $N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
. Therefore, Lemma 2.7(b) gives that
$N_S(Q_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(Q_i))$
. Therefore, Lemma 2.7(b) gives that
![]() $n_i\in O^p(N_{\mathcal {N}}(R_i))$
,
$n_i\in O^p(N_{\mathcal {N}}(R_i))$
,
![]() $N_{\mathcal {N} S}(R_i)/R_i$
has a strongly p-embedded subgroup and
$N_{\mathcal {N} S}(R_i)/R_i$
has a strongly p-embedded subgroup and
![]() $N_S(R_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(R_i))$
for
$N_S(R_i)\in \mathrm {Syl}_p(N_{\mathcal {N} S}(R_i))$
for
![]() $i=1,\dots ,k$
. In particular,
$i=1,\dots ,k$
. In particular,
![]() $O_p(N_{\mathcal {N} S}(R_i)/R_i)=1$
and thus
$O_p(N_{\mathcal {N} S}(R_i)/R_i)=1$
and thus
![]() $O_p(N_{\mathcal {N} S}(R_i))=R_i$
(cf. [Reference Aschbacher, Kessar and Oliver1, Proposition A.7(c)]).
$O_p(N_{\mathcal {N} S}(R_i))=R_i$
(cf. [Reference Aschbacher, Kessar and Oliver1, Proposition A.7(c)]).
For all
![]() $i=1,\dots ,k$
it follows from Lemma 2.8 that
$i=1,\dots ,k$
it follows from Lemma 2.8 that
 $Q_i=S_{g_i}=S_{m_i}^{s_i^{-1}}$
. Because
$Q_i=S_{g_i}=S_{m_i}^{s_i^{-1}}$
. Because
![]() $s_i\in N_S(Q_i)$
, this implies
$s_i\in N_S(Q_i)$
, this implies
In particular,
![]() $R_k=Q_k=S_{m_k}=S_{n_k}$
. Moreover, because
$R_k=Q_k=S_{m_k}=S_{n_k}$
. Moreover, because
![]() $(m_i,Q_i)$
is conjugate to
$(m_i,Q_i)$
is conjugate to
![]() $(n_i,R_i)$
under
$(n_i,R_i)$
under
![]() $x_{i+1}\in S$
for
$x_{i+1}\in S$
for
![]() $1\leq i<k$
, Lemma 2.8 gives also
$1\leq i<k$
, Lemma 2.8 gives also
![]() $R_i=S_{n_i}$
for
$R_i=S_{n_i}$
for
![]() $1\leq i<k$
. So (ii) holds. Note now that
$1\leq i<k$
. So (ii) holds. Note now that
![]() $u':=(t^{-1},t,n_1,\dots ,n_k,n^{-1})\in \mathbf {D}$
via
$u':=(t^{-1},t,n_1,\dots ,n_k,n^{-1})\in \mathbf {D}$
via
![]() $S_n^t$
and
$S_n^t$
and
![]() $t^{-1}=\Pi (t^{-1},n,n^{-1})=\Pi (u')=\Pi (n_1,\dots ,n_k,n^{-1})\in S\cap \mathcal {N}$
. Hence,
$t^{-1}=\Pi (t^{-1},n,n^{-1})=\Pi (u')=\Pi (n_1,\dots ,n_k,n^{-1})\in S\cap \mathcal {N}$
. Hence,
![]() $t\in \mathcal {N}\cap S$
and the proof is complete.
$t\in \mathcal {N}\cap S$
and the proof is complete.
6.2. Partial normal subgroups of linking localities
In this subsection, we will first prove Theorem C. Afterwards, we prove as a corollary that any two linking localities over the same fusion system have the same number of partial normal subgroups. Against our usual convention, we will use the left-hand notation for the map
![]() $\Phi _{\mathcal L^+,\mathcal L}$
from Theorem C. Recall that
$\Phi _{\mathcal L^+,\mathcal L}$
from Theorem C. Recall that
![]() ${\mathfrak {N}}(\mathcal L)$
denotes the set of partial normal subgroups of a partial groups
${\mathfrak {N}}(\mathcal L)$
denotes the set of partial normal subgroups of a partial groups
![]() $\mathcal L$
. We first show the following lemma.
$\mathcal L$
. We first show the following lemma.
Lemma 6.3. Let
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\Delta \subseteq \Delta ^+$
and
$\Delta \subseteq \Delta ^+$
and
![]() $\mathcal L=\mathcal L^+|_\Delta $
. Assume that every proper overgroup of an element of
$\mathcal L=\mathcal L^+|_\Delta $
. Assume that every proper overgroup of an element of
![]() $\Delta ^+\backslash \Delta $
is in
$\Delta ^+\backslash \Delta $
is in
![]() $\Delta $
. Let
$\Delta $
. Let
![]() $\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
,
$\mathcal {N}^+\in {\mathfrak {N}}(\mathcal L^+)$
,
![]() $\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
and set
$\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
and set
![]() $T:=\mathcal {N}^+\cap S=\mathcal {N}\cap S$
. Then the following hold.
$T:=\mathcal {N}^+\cap S=\mathcal {N}\cap S$
. Then the following hold.
-
(a)
 $\mathcal {N}^+=\langle \mathcal {N}^{\mathcal L^+}\rangle $
, where
$\mathcal {N}^+=\langle \mathcal {N}^{\mathcal L^+}\rangle $
, where
 $\langle \mathcal {N}^{\mathcal L^+}\rangle $
denotes the smallest partial subgroup of
$\langle \mathcal {N}^{\mathcal L^+}\rangle $
denotes the smallest partial subgroup of
 $\mathcal L^+$
containing all of the elements of the form
$\mathcal L^+$
containing all of the elements of the form
 $n^f$
with
$n^f$
with
 $f\in \mathcal L^+$
and
$f\in \mathcal L^+$
and
 $n\in \mathcal {N}\cap \mathbf {D}^+(f)$
.
$n\in \mathcal {N}\cap \mathbf {D}^+(f)$
. -
(b) If
 $\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
$\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
 $\mathcal {F}$
-invariant, then
$\mathcal {F}$
-invariant, then
 $\mathcal {F}_T(\mathcal {N})=\mathcal {F}_T(\mathcal {N}^+)$
.
$\mathcal {F}_T(\mathcal {N})=\mathcal {F}_T(\mathcal {N}^+)$
. -
(c) Let
 $\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
and
$\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
and
 $\mathcal {K}:=\mathcal {K}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
. Then
$\mathcal {K}:=\mathcal {K}^+\cap \mathcal L\in {\mathfrak {N}}(\mathcal L)$
. Then
 $\mathcal {K}^+T=\mathcal {N}^+$
if and only if
$\mathcal {K}^+T=\mathcal {N}^+$
if and only if
 $\mathcal {K} T=\mathcal {N}$
.
$\mathcal {K} T=\mathcal {N}$
.
Proof. Observe that, for any
![]() $k\in \mathcal L^+$
and
$k\in \mathcal L^+$
and
![]() $t\in S$
, we have
$t\in S$
, we have
![]() $S_{kt}=S_{(k,t)}=S_k$
. Hence,
$S_{kt}=S_{(k,t)}=S_k$
. Hence,
![]() $kt\in \mathcal L$
if and only if
$kt\in \mathcal L$
if and only if
![]() $k\in \mathcal L$
. With
$k\in \mathcal L$
. With
![]() $\mathcal {K}^+$
and
$\mathcal {K}^+$
and
![]() $\mathcal {K}$
as in (c), it follows that
$\mathcal {K}$
as in (c), it follows that
![]() $\mathcal {K}^+T\cap \mathcal L=(\mathcal {K}^+\cap \mathcal L)T=\mathcal {K} T$
. Hence, if
$\mathcal {K}^+T\cap \mathcal L=(\mathcal {K}^+\cap \mathcal L)T=\mathcal {K} T$
. Hence, if
![]() $\mathcal {K}^+ T=\mathcal {N}^+$
, then
$\mathcal {K}^+ T=\mathcal {N}^+$
, then
![]() $\mathcal {N}=\mathcal {N}^+\cap \mathcal L=(\mathcal {K}^+ T)\cap \mathcal L=\mathcal {K} T$
. On the other hand, if
$\mathcal {N}=\mathcal {N}^+\cap \mathcal L=(\mathcal {K}^+ T)\cap \mathcal L=\mathcal {K} T$
. On the other hand, if
![]() $\mathcal {K} T=\mathcal {N}$
and (a) holds, then
$\mathcal {K} T=\mathcal {N}$
and (a) holds, then
![]() $\mathcal {K}\subseteq \mathcal {N}$
and so
$\mathcal {K}\subseteq \mathcal {N}$
and so
![]() $\mathcal {K}^+=\langle \mathcal {K}^{\mathcal L^+}\rangle \subseteq \langle \mathcal {N}^{\mathcal L^+}\rangle =\mathcal {N}^+$
. Thus, because
$\mathcal {K}^+=\langle \mathcal {K}^{\mathcal L^+}\rangle \subseteq \langle \mathcal {N}^{\mathcal L^+}\rangle =\mathcal {N}^+$
. Thus, because
![]() $\mathcal {N}^+$
is a partial subgroup, it follows in this case that
$\mathcal {N}^+$
is a partial subgroup, it follows in this case that
![]() $\mathcal {K}^+T\subseteq \mathcal {N}^+$
. Hence, it remains to prove (a), (b) and the following property:
$\mathcal {K}^+T\subseteq \mathcal {N}^+$
. Hence, it remains to prove (a), (b) and the following property:
Set
![]() $\mathcal {E}:=\mathcal {F}_T(\mathcal {N})$
. Because
$\mathcal {E}:=\mathcal {F}_T(\mathcal {N})$
. Because
![]() $\mathcal {N}\subseteq \mathcal {N}^+\unlhd \mathcal L^+$
, we have
$\mathcal {N}\subseteq \mathcal {N}^+\unlhd \mathcal L^+$
, we have
![]() $\langle \mathcal {N}^{\mathcal L^+}\rangle \subseteq \mathcal {N}^+$
. Moreover, clearly,
$\langle \mathcal {N}^{\mathcal L^+}\rangle \subseteq \mathcal {N}^+$
. Moreover, clearly,
![]() $\mathcal {E}=\mathcal {F}_T(\mathcal {N})\subseteq \mathcal {F}_T(\mathcal {N}^+)$
. So fixing
$\mathcal {E}=\mathcal {F}_T(\mathcal {N})\subseteq \mathcal {F}_T(\mathcal {N}^+)$
. So fixing
![]() $n\in \mathcal {N}^+$
, we need to show that
$n\in \mathcal {N}^+$
, we need to show that
![]() $n\in \langle \mathcal {N}^{\mathcal L^+}\rangle $
and, if
$n\in \langle \mathcal {N}^{\mathcal L^+}\rangle $
and, if
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() $\mathcal {F}$
-invariant, then
$\mathcal {F}$
-invariant, then
![]() $c_n\colon S_n\cap T\longrightarrow T$
is a morphism in
$c_n\colon S_n\cap T\longrightarrow T$
is a morphism in
![]() $\mathcal {E}$
. Furthermore, fixing
$\mathcal {E}$
. Furthermore, fixing
![]() $\mathcal {K}^+$
and
$\mathcal {K}^+$
and
![]() $\mathcal {K}$
as in (c) such that
$\mathcal {K}$
as in (c) such that
![]() $\mathcal {K} T=\mathcal {N}$
, we need to show that
$\mathcal {K} T=\mathcal {N}$
, we need to show that
![]() $n\in \mathcal {K}^+ T$
.
$n\in \mathcal {K}^+ T$
.
Because
![]() $S_{(k,t)}=S_{kt}$
for all
$S_{(k,t)}=S_{kt}$
for all
![]() $k\in \mathcal {K}^+$
and
$k\in \mathcal {K}^+$
and
![]() $t\in T$
, using the Frattini calculus [Reference Chermak7, Lemma 3.4], one sees that
$t\in T$
, using the Frattini calculus [Reference Chermak7, Lemma 3.4], one sees that
![]() $\mathcal {K}^+ T=T\mathcal {K}^+$
is a subgroup of
$\mathcal {K}^+ T=T\mathcal {K}^+$
is a subgroup of
![]() $\mathcal L^+$
. So by Lemma 6.2 applied with
$\mathcal L^+$
. So by Lemma 6.2 applied with
![]() $\mathcal L^+$
and
$\mathcal L^+$
and
![]() $\mathcal {N}^+$
in place of
$\mathcal {N}^+$
in place of
![]() $\mathcal L$
and
$\mathcal L$
and
![]() $\mathcal {N}$
, we may assume that
$\mathcal {N}$
, we may assume that
![]() $P=S_n\in \Delta ^+$
and
$P=S_n\in \Delta ^+$
and
![]() $n\in O^p(N_{\mathcal {N}^+}(P))$
. If
$n\in O^p(N_{\mathcal {N}^+}(P))$
. If
![]() $P\in \Delta $
, then
$P\in \Delta $
, then
![]() $N_{\mathcal L^+}(P)=N_{\mathcal L}(P)$
and
$N_{\mathcal L^+}(P)=N_{\mathcal L}(P)$
and
![]() $n\in N_{\mathcal {N}^+}(P)=N_{\mathcal {N}}(P)$
because
$n\in N_{\mathcal {N}^+}(P)=N_{\mathcal {N}}(P)$
because
![]() $\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. So in this case,
$\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. So in this case,
![]() $n\in \langle \mathcal {N}^{\mathcal L^+}\rangle $
, the conjugation homomorphism
$n\in \langle \mathcal {N}^{\mathcal L^+}\rangle $
, the conjugation homomorphism
![]() $c_n|_{P\cap T}$
is a morphism in
$c_n|_{P\cap T}$
is a morphism in
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $n\in \mathcal {N}=\mathcal {K} T\subseteq \mathcal {K}^+ T$
.
$n\in \mathcal {N}=\mathcal {K} T\subseteq \mathcal {K}^+ T$
.
Suppose now that
![]() $P\in \Delta ^+\backslash \Delta $
. Then by Lemma 2.10(a), there exists
$P\in \Delta ^+\backslash \Delta $
. Then by Lemma 2.10(a), there exists
![]() $f\in \mathcal L^+$
such that
$f\in \mathcal L^+$
such that
![]() $P\leq S_f$
and
$P\leq S_f$
and
![]() $R:=P^f$
is fully
$R:=P^f$
is fully
![]() $\mathcal {F}$
-normalised. By Lemma 2.7(b), the conjugation map
$\mathcal {F}$
-normalised. By Lemma 2.7(b), the conjugation map
![]() $c_f\colon N_{\mathcal L^+}(P)\longrightarrow N_{\mathcal L^+}(R)$
is defined and an isomorphism of groups. In particular,
$c_f\colon N_{\mathcal L^+}(P)\longrightarrow N_{\mathcal L^+}(R)$
is defined and an isomorphism of groups. In particular,
![]() $n^f\in O^p(N_{\mathcal {N}^+}(P))^f\subseteq O^p(N_{\mathcal {N}^+}(R))=O^p(N_{\mathcal {N}}(R))$
, where the last equality uses
$n^f\in O^p(N_{\mathcal {N}^+}(P))^f\subseteq O^p(N_{\mathcal {N}^+}(R))=O^p(N_{\mathcal {N}}(R))$
, where the last equality uses
![]() $\mathcal L\cap \mathcal {N}^+=\mathcal {N}$
and
$\mathcal L\cap \mathcal {N}^+=\mathcal {N}$
and
![]() $N_{\mathcal L^+}(R)=N_{\mathcal L}(R)$
by Lemma 2.26. Hence, using Lemma 2.7(c), we see that
$N_{\mathcal L^+}(R)=N_{\mathcal L}(R)$
by Lemma 2.26. Hence, using Lemma 2.7(c), we see that
 $n=(n^f)^{f^{-1}}\subseteq N_{\mathcal {N}}(R)^{f^{-1}}\subseteq \langle \mathcal {N}^{\mathcal L^+}\rangle $
, proving (a).
$n=(n^f)^{f^{-1}}\subseteq N_{\mathcal {N}}(R)^{f^{-1}}\subseteq \langle \mathcal {N}^{\mathcal L^+}\rangle $
, proving (a).
Because
![]() $\mathcal {N}=\mathcal {K} T\subseteq \mathcal {K} S$
, Lemma 6.1(b) applied with
$\mathcal {N}=\mathcal {K} T\subseteq \mathcal {K} S$
, Lemma 6.1(b) applied with
![]() $\mathcal {K}$
in place of
$\mathcal {K}$
in place of
![]() $\mathcal {N}$
gives that
$\mathcal {N}$
gives that
![]() $n^f\in O^p(N_{\mathcal {N}}(R))\subseteq O^p(N_{\mathcal {K} S}(R))=O^p(N_{\mathcal {K}}(R))$
. Hence, we have
$n^f\in O^p(N_{\mathcal {N}}(R))\subseteq O^p(N_{\mathcal {K} S}(R))=O^p(N_{\mathcal {K}}(R))$
. Hence, we have
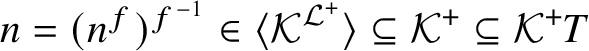 $n=(n^f)^{f^{-1}}\in \langle \mathcal {K}^{\mathcal L^+}\rangle \subseteq \mathcal {K}^+\subseteq \mathcal {K}^+ T$
, proving (6.3.1) and thus (c).
$n=(n^f)^{f^{-1}}\in \langle \mathcal {K}^{\mathcal L^+}\rangle \subseteq \mathcal {K}^+\subseteq \mathcal {K}^+ T$
, proving (6.3.1) and thus (c).
For the proof of (b), note that
![]() $c_{n^f}|_{R\cap T}\in \mathrm {Aut}_{\mathcal {E}}(R\cap T)$
. Define
$c_{n^f}|_{R\cap T}\in \mathrm {Aut}_{\mathcal {E}}(R\cap T)$
. Define
![]() $\varphi :=c_f|_{P\cap T}\in \mathrm {Hom}_{\mathcal {F}}(P\cap T,R\cap T)$
. For every
$\varphi :=c_f|_{P\cap T}\in \mathrm {Hom}_{\mathcal {F}}(P\cap T,R\cap T)$
. For every
![]() $x\in R$
, we have
$x\in R$
, we have
![]() $(f^{-1},n,f,x,f^{-1},n,f)\in \mathbf {D}^+$
via R, and so
$(f^{-1},n,f,x,f^{-1},n,f)\in \mathbf {D}^+$
via R, and so
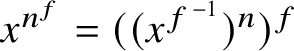 $x^{n^f}=((x^{f^{-1}})^n)^f$
. Hence,
$x^{n^f}=((x^{f^{-1}})^n)^f$
. Hence,
![]() $\varphi ^{-1}(c_n|_{P\cap T})\varphi =c_{n^f}|_{R\cap T}\in \mathrm {Aut}_{\mathcal {E}}(R\cap T)$
. If
$\varphi ^{-1}(c_n|_{P\cap T})\varphi =c_{n^f}|_{R\cap T}\in \mathrm {Aut}_{\mathcal {E}}(R\cap T)$
. If
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() $\mathcal {F}$
-invariant, using the characterisation of
$\mathcal {F}$
-invariant, using the characterisation of
![]() $\mathcal {F}$
-invariant subsystems given in [Reference Aschbacher, Kessar and Oliver1, Proposition I.6.4(d)], we can conclude that
$\mathcal {F}$
-invariant subsystems given in [Reference Aschbacher, Kessar and Oliver1, Proposition I.6.4(d)], we can conclude that
![]() $c_n|_{P\cap T}=\varphi (c_{n^f}|_{R\cap T}) \varphi ^{-1}\in \mathrm {Aut}_{\mathcal {E}}(P\cap T)$
. This shows (b) and completes the proof.
$c_n|_{P\cap T}=\varphi (c_{n^f}|_{R\cap T}) \varphi ^{-1}\in \mathrm {Aut}_{\mathcal {E}}(P\cap T)$
. This shows (b) and completes the proof.
Proof of Theorem C. For every partial normal subgroup
![]() $\mathcal {N}^+$
of
$\mathcal {N}^+$
of
![]() $\mathcal L^+$
, it is easy to see that the intersection
$\mathcal L^+$
, it is easy to see that the intersection
![]() $\mathcal {N}^+\cap \mathcal L$
is a partial normal subgroup of
$\mathcal {N}^+\cap \mathcal L$
is a partial normal subgroup of
![]() $\mathcal L$
. Hence, the map
$\mathcal L$
. Hence, the map
is well defined. Moreover, this map is clearly inclusion preserving.
Without loss of generality, assume that
![]() $\Delta \neq \Delta ^+$
. Let
$\Delta \neq \Delta ^+$
. Let
![]() $R\in \Delta ^+\backslash \Delta $
be of maximal order. Because
$R\in \Delta ^+\backslash \Delta $
be of maximal order. Because
![]() $\Delta ^+$
and
$\Delta ^+$
and
![]() $\Delta $
are closed under
$\Delta $
are closed under
![]() $\mathcal {F}$
-conjugacy,
$\mathcal {F}$
-conjugacy,
![]() $\Delta ^*:=\Delta \cup R^{\mathcal {F}}$
is closed under
$\Delta ^*:=\Delta \cup R^{\mathcal {F}}$
is closed under
![]() $\mathcal {F}$
-conjugacy and contained in
$\mathcal {F}$
-conjugacy and contained in
![]() $\Delta ^+$
. If P is a proper overgroup of an element of
$\Delta ^+$
. If P is a proper overgroup of an element of
![]() $R^{\mathcal {F}}$
, then
$R^{\mathcal {F}}$
, then
![]() $P\in \Delta ^+$
as
$P\in \Delta ^+$
as
![]() $\Delta ^+$
is overgroup closed, so the maximality of
$\Delta ^+$
is overgroup closed, so the maximality of
![]() $|R|$
yields
$|R|$
yields
![]() $P\in \Delta $
. Because
$P\in \Delta $
. Because
![]() $\Delta $
is overgroup closed, this shows that
$\Delta $
is overgroup closed, this shows that
![]() $\Delta ^*$
is
$\Delta ^*$
is
![]() $\mathcal {F}$
-closed and
$\mathcal {F}$
-closed and
![]() $\mathcal L^*:=\mathcal L^+|_{\Delta ^*}$
is well defined. Notice that
$\mathcal L^*:=\mathcal L^+|_{\Delta ^*}$
is well defined. Notice that
![]() $\mathcal {F}^{cr}\subseteq \Delta \subseteq \Delta ^*$
and
$\mathcal {F}^{cr}\subseteq \Delta \subseteq \Delta ^*$
and
![]() $N_{\mathcal L^*}(P)=N_{\mathcal L^+}(P)$
is of characteristic p for every
$N_{\mathcal L^*}(P)=N_{\mathcal L^+}(P)$
is of characteristic p for every
![]() $P\in \Delta ^*$
. Therefore,
$P\in \Delta ^*$
. Therefore,
![]() $(\mathcal L^*,\Delta ^*,S)$
is a linking locality over
$(\mathcal L^*,\Delta ^*,S)$
is a linking locality over
![]() $\mathcal {F}$
. So, similarly, we have maps
$\mathcal {F}$
. So, similarly, we have maps
and
defined. Notice that
![]() $\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^*,\mathcal L}\circ \Phi _{\mathcal L^+,\mathcal L^*}$
. By induction on
$\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^*,\mathcal L}\circ \Phi _{\mathcal L^+,\mathcal L^*}$
. By induction on
![]() $|\Delta ^+\backslash \Delta |$
, we may assume that the assertion is true with
$|\Delta ^+\backslash \Delta |$
, we may assume that the assertion is true with
![]() $(\mathcal L^*,\Delta ^*,S)$
in place of
$(\mathcal L^*,\Delta ^*,S)$
in place of
![]() $(\mathcal L,\Delta ,S)$
. That means that
$(\mathcal L,\Delta ,S)$
. That means that
![]() $\Phi _{\mathcal L^+,\mathcal L^*}$
is a bijection such that
$\Phi _{\mathcal L^+,\mathcal L^*}$
is a bijection such that
 $\Phi _{\mathcal L^+,\mathcal L^*}^{-1}$
is inclusion preserving; moreover, given
$\Phi _{\mathcal L^+,\mathcal L^*}^{-1}$
is inclusion preserving; moreover, given
![]() $\mathcal {N}^+\unlhd \mathcal L^+$
and
$\mathcal {N}^+\unlhd \mathcal L^+$
and
![]() $\mathcal {N}^*=\mathcal {N}^+\cap \mathcal L^*\unlhd \mathcal L^*$
such that
$\mathcal {N}^*=\mathcal {N}^+\cap \mathcal L^*\unlhd \mathcal L^*$
such that
![]() $\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)$
is normal in
$\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)$
is normal in
![]() $\mathcal {F}$
, we have
$\mathcal {F}$
, we have
![]() $\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)$
; also, if
$\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)$
; also, if
![]() $\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
,
$\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
,
![]() $\mathcal {K}^*=\mathcal {K}^+\cap \mathcal L^*$
,
$\mathcal {K}^*=\mathcal {K}^+\cap \mathcal L^*$
,
![]() $\mathcal {N}^*=\mathcal {N}^+\cap \mathcal L^*$
and
$\mathcal {N}^*=\mathcal {N}^+\cap \mathcal L^*$
and
![]() $T=S\cap \mathcal {N}^+=S\cap \mathcal {N}^*$
, then
$T=S\cap \mathcal {N}^+=S\cap \mathcal {N}^*$
, then
![]() $\mathcal {K}^+T=\mathcal {N}^+$
if and only if
$\mathcal {K}^+T=\mathcal {N}^+$
if and only if
![]() $\mathcal {K}^*T=\mathcal {N}^*$
.
$\mathcal {K}^*T=\mathcal {N}^*$
.
As noted above, every proper overgroup of an element of
![]() $\Delta ^*\backslash \Delta =R^{\mathcal {F}}$
is in
$\Delta ^*\backslash \Delta =R^{\mathcal {F}}$
is in
![]() $\Delta $
. Hence, by Lemma 6.3(b),(c), properties (b) and (c) hold with
$\Delta $
. Hence, by Lemma 6.3(b),(c), properties (b) and (c) hold with
![]() $(\mathcal L^*,\Delta ^*,S)$
in place of
$(\mathcal L^*,\Delta ^*,S)$
in place of
![]() $(\mathcal L^+,\Delta ^+,S)$
. Suppose now that
$(\mathcal L^+,\Delta ^+,S)$
. Suppose now that
![]() $\mathcal {N}^+$
is a partial normal subgroup of
$\mathcal {N}^+$
is a partial normal subgroup of
![]() $\mathcal L^+$
and
$\mathcal L^+$
and
![]() $\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\unlhd \mathcal L$
such that
$\mathcal {N}:=\mathcal {N}^+\cap \mathcal L\unlhd \mathcal L$
such that
![]() $\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
$\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
is
![]() $\mathcal {F}$
-invariant. Then
$\mathcal {F}$
-invariant. Then
![]() $\mathcal {N}^*:=\mathcal {N}^+\cap \mathcal L^*\unlhd \mathcal L^*$
with
$\mathcal {N}^*:=\mathcal {N}^+\cap \mathcal L^*\unlhd \mathcal L^*$
with
![]() $\mathcal {N}^*\cap \mathcal L=\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. Because (b) is true with
$\mathcal {N}^*\cap \mathcal L=\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. Because (b) is true with
![]() $(\mathcal L^*,\Delta ^*,S)$
in place of
$(\mathcal L^*,\Delta ^*,S)$
in place of
![]() $(\mathcal L^+,\Delta ^+,S)$
, it follows that
$(\mathcal L^+,\Delta ^+,S)$
, it follows that
![]() $\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
and, in particular,
$\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
and, in particular,
![]() $\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)$
is
$\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)$
is
![]() $\mathcal {F}$
-invariant. So
$\mathcal {F}$
-invariant. So
![]() $\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)=\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
. This proves (b).
$\mathcal {F}_{S\cap \mathcal {N}^+}(\mathcal {N}^+)=\mathcal {F}_{S\cap \mathcal {N}^*}(\mathcal {N}^*)=\mathcal {F}_{S\cap \mathcal {N}}(\mathcal {N})$
. This proves (b).
If
![]() $\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
are arbitrary,
$\mathcal {N}^+,\mathcal {K}^+\in {\mathfrak {N}}(\mathcal L^+)$
are arbitrary,
![]() $\mathcal {N}^*:=\mathcal L^*\cap \mathcal {N}^+$
,
$\mathcal {N}^*:=\mathcal L^*\cap \mathcal {N}^+$
,
![]() $\mathcal {K}^*:=\mathcal L^*\cap \mathcal {N}^+$
,
$\mathcal {K}^*:=\mathcal L^*\cap \mathcal {N}^+$
,
![]() $\mathcal {N}:=\mathcal L\cap \mathcal {N}^+$
,
$\mathcal {N}:=\mathcal L\cap \mathcal {N}^+$
,
![]() $\mathcal {K}:=\mathcal L\cap \mathcal {K}^+$
and
$\mathcal {K}:=\mathcal L\cap \mathcal {K}^+$
and
![]() $T:=S\cap \mathcal {N}$
, then we see similarly that
$T:=S\cap \mathcal {N}$
, then we see similarly that
and (c) holds. Hence, it remains to prove (a).
If (a) is true with
![]() $(\mathcal L^*,\Delta ^*,S)$
in place of
$(\mathcal L^*,\Delta ^*,S)$
in place of
![]() $(\mathcal L^+,\Delta ^+,S)$
, then
$(\mathcal L^+,\Delta ^+,S)$
, then
![]() $\Phi _{\mathcal L^*,\mathcal L}$
is a bijection and
$\Phi _{\mathcal L^*,\mathcal L}$
is a bijection and
 $\Phi _{\mathcal L^*,\mathcal L}^{-1}$
is inclusion preserving. Hence,
$\Phi _{\mathcal L^*,\mathcal L}^{-1}$
is inclusion preserving. Hence,
![]() $\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^*,\mathcal L}\circ \Phi _{\mathcal L^+,\mathcal L^*}$
is a bijection and
$\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^*,\mathcal L}\circ \Phi _{\mathcal L^+,\mathcal L^*}$
is a bijection and
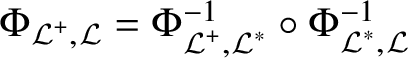 $\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^+,\mathcal L^*}^{-1}\circ \Phi _{\mathcal L^*,\mathcal L}^{-1}$
is inclusion preserving. Thus, replacing
$\Phi _{\mathcal L^+,\mathcal L}=\Phi _{\mathcal L^+,\mathcal L^*}^{-1}\circ \Phi _{\mathcal L^*,\mathcal L}^{-1}$
is inclusion preserving. Thus, replacing
![]() $(\mathcal L^+,\Delta ^+,S)$
by
$(\mathcal L^+,\Delta ^+,S)$
by
![]() $(\mathcal L^*,\Delta ^*,S)$
, we may assume from now on that
$(\mathcal L^*,\Delta ^*,S)$
, we may assume from now on that
Then, in particular, every proper overgroup of an element of
![]() $\Delta ^+\backslash \Delta =R^{\mathcal {F}}$
is an element of
$\Delta ^+\backslash \Delta =R^{\mathcal {F}}$
is an element of
![]() $\Delta $
. So by Lemma 2.26,
$\Delta $
. So by Lemma 2.26,
![]() $N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of
$N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of
![]() $\mathcal L$
.
$\mathcal L$
.
Note that Lemma 6.3(a) implies that
![]() $\Phi _{\mathcal L^+,\mathcal L}$
is injective. Moreover, if
$\Phi _{\mathcal L^+,\mathcal L}$
is injective. Moreover, if
![]() $\mathcal {M}^+$
and
$\mathcal {M}^+$
and
![]() $\mathcal {N}^+$
are partial normal subgroups of
$\mathcal {N}^+$
are partial normal subgroups of
![]() $\mathcal L^+$
with
$\mathcal L^+$
with
![]() $\mathcal {M}^+\cap \mathcal L\subseteq \mathcal {N}^+\cap \mathcal L$
, then Lemma 6.3(a) gives that
$\mathcal {M}^+\cap \mathcal L\subseteq \mathcal {N}^+\cap \mathcal L$
, then Lemma 6.3(a) gives that
![]() $\mathcal {M}^+=\langle (\mathcal {M}^+\cap \mathcal L)^{\mathcal L^+}\rangle \subseteq \mathcal {N}^+=\langle (\mathcal {N}^+\cap \mathcal L)^{\mathcal L^+}\rangle $
. So if
$\mathcal {M}^+=\langle (\mathcal {M}^+\cap \mathcal L)^{\mathcal L^+}\rangle \subseteq \mathcal {N}^+=\langle (\mathcal {N}^+\cap \mathcal L)^{\mathcal L^+}\rangle $
. So if
![]() $\Phi _{\mathcal L^+,\mathcal L}$
is a bijection, then
$\Phi _{\mathcal L^+,\mathcal L}$
is a bijection, then
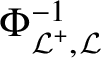 $\Phi _{\mathcal L^+,\mathcal L}^{-1}$
is inclusion preserving. Hence, it remains to show that
$\Phi _{\mathcal L^+,\mathcal L}^{-1}$
is inclusion preserving. Hence, it remains to show that
![]() $\Phi _{\mathcal L^+,\mathcal L}$
is surjective.
$\Phi _{\mathcal L^+,\mathcal L}$
is surjective.
For the remainder of this proof let
![]() $\mathcal {N}$
be a partial normal subgroup of
$\mathcal {N}$
be a partial normal subgroup of
![]() $\mathcal L$
and set
$\mathcal L$
and set
![]() $T:=S\cap \mathcal {N}$
. We will show that there exists
$T:=S\cap \mathcal {N}$
. We will show that there exists
![]() $\mathcal {N}^+\unlhd \mathcal L^+$
with
$\mathcal {N}^+\unlhd \mathcal L^+$
with
![]() $\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. For the proof we set
$\mathcal {N}^+\cap \mathcal L=\mathcal {N}$
. For the proof we set
![]() $\overline {\mathcal L}:=\mathcal L/\mathcal {N}$
and consider the natural projection
$\overline {\mathcal L}:=\mathcal L/\mathcal {N}$
and consider the natural projection
By [Reference Chermak7, Corollary 4.5], using the ‘bar notation’, the triple
![]() $(\overline {\mathcal L},\overline {\Delta },\overline {S})$
is a locality. Observe also that
$(\overline {\mathcal L},\overline {\Delta },\overline {S})$
is a locality. Observe also that
 $N_{\mathcal L}(R)\alpha \subseteq N_{\overline {\mathcal L}}(\overline {R})$
. We consider two cases now.
$N_{\mathcal L}(R)\alpha \subseteq N_{\overline {\mathcal L}}(\overline {R})$
. We consider two cases now.
Case 1:
![]() $T\not \leq R$
. Because T is strongly closed in
$T\not \leq R$
. Because T is strongly closed in
![]() $\mathcal {F}$
by [Reference Chermak7, Lemma 3.1], it follows then that
$\mathcal {F}$
by [Reference Chermak7, Lemma 3.1], it follows then that
![]() $T\not \leq Q$
for every
$T\not \leq Q$
for every
![]() $Q\in R^{\mathcal {F}}$
. Thus, for any such Q, we have
$Q\in R^{\mathcal {F}}$
. Thus, for any such Q, we have
![]() $QT\in \Delta $
and
$QT\in \Delta $
and
![]() $Q\alpha =\overline {Q}=\overline {QT}\in \overline {\Delta }$
. This proves
$Q\alpha =\overline {Q}=\overline {QT}\in \overline {\Delta }$
. This proves
![]() $\Delta ^+\alpha \subseteq \overline {\Delta }$
. Applying Corollary 3.3 with
$\Delta ^+\alpha \subseteq \overline {\Delta }$
. Applying Corollary 3.3 with
![]() $(\overline {\mathcal L},\overline {\Delta },\overline {S})$
in place of
$(\overline {\mathcal L},\overline {\Delta },\overline {S})$
in place of
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
, we conclude that there exists a homomorphism of partial group
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },{\widetilde {S}})$
, we conclude that there exists a homomorphism of partial group
![]() $\gamma \colon \mathcal L^+\longrightarrow \overline {\mathcal L}$
with
$\gamma \colon \mathcal L^+\longrightarrow \overline {\mathcal L}$
with
![]() $\gamma |_{\mathcal L}=\alpha $
. By [Reference Chermak6, Lemma 3.3],
$\gamma |_{\mathcal L}=\alpha $
. By [Reference Chermak6, Lemma 3.3],
![]() $\mathcal {N}^+:=\ker (\gamma )$
is a partial normal subgroup of
$\mathcal {N}^+:=\ker (\gamma )$
is a partial normal subgroup of
![]() $\mathcal L^+$
. Moreover,
$\mathcal L^+$
. Moreover,
![]() $\mathcal {N}^+\cap \mathcal L=\ker (\alpha )=\mathcal {N}$
.
$\mathcal {N}^+\cap \mathcal L=\ker (\alpha )=\mathcal {N}$
.
Case 2:
![]() $T\leq R$
. In this case, by Lemma 2.21(a),
$T\leq R$
. In this case, by Lemma 2.21(a),
 $N_{\mathcal L}(R)\alpha =N_{\overline {\mathcal L}}(\overline {R})$
. Because
$N_{\mathcal L}(R)\alpha =N_{\overline {\mathcal L}}(\overline {R})$
. Because
![]() $N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of
$N_{\mathcal L}(R)=N_{\mathcal L^+}(R)$
is a subgroup of
![]() $\mathcal L$
, it follows now from Lemma 2.19 that
$\mathcal L$
, it follows now from Lemma 2.19 that
 $M:=N_{\overline {\mathcal L}}(\overline {R})$
is a subgroup of
$M:=N_{\overline {\mathcal L}}(\overline {R})$
is a subgroup of
![]() $\overline {\mathcal L}$
and
$\overline {\mathcal L}$
and
![]() $\alpha |_{N_{\mathcal L}(R)}\colon N_{\mathcal L}(R)\longrightarrow M$
is a surjective group homomorphism. Because
$\alpha |_{N_{\mathcal L}(R)}\colon N_{\mathcal L}(R)\longrightarrow M$
is a surjective group homomorphism. Because
![]() $N_S(R)\in \mathrm {Syl}_p(N_{\mathcal L}(R))$
by Lemma 2.10(b), this yields that
$N_S(R)\in \mathrm {Syl}_p(N_{\mathcal L}(R))$
by Lemma 2.10(b), this yields that
 $N_{\overline {S}}(\overline {R})=N_S(R)\alpha $
is a Sylow p-subgroup of M. Moreover, because
$N_{\overline {S}}(\overline {R})=N_S(R)\alpha $
is a Sylow p-subgroup of M. Moreover, because
![]() $N_{\mathcal {F}}(R)=\mathcal {F}_{N_S(R)}(N_{\mathcal L^+}(R))=\mathcal {F}_{N_S(R)}(N_{\mathcal L}(R))$
by Lemma 2.10(c), it follows from Lemma 2.15 that
$N_{\mathcal {F}}(R)=\mathcal {F}_{N_S(R)}(N_{\mathcal L^+}(R))=\mathcal {F}_{N_S(R)}(N_{\mathcal L}(R))$
by Lemma 2.10(c), it follows from Lemma 2.15 that
![]() $\alpha |_{N_S(R)}$
induces and epimorphism from
$\alpha |_{N_S(R)}$
induces and epimorphism from
![]() $N_{\mathcal {F}}(R)$
to
$N_{\mathcal {F}}(R)$
to
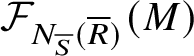 $\mathcal {F}_{N_{\overline {S}}(\overline {R})}(M)$
.
$\mathcal {F}_{N_{\overline {S}}(\overline {R})}(M)$
.
By Lemma 2.21(b),
![]() $\alpha |_S$
induces an epimorphism from
$\alpha |_S$
induces an epimorphism from
![]() $\mathcal {F}=\mathcal {F}_S(\mathcal L)$
to
$\mathcal {F}=\mathcal {F}_S(\mathcal L)$
to
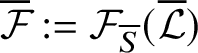 $\overline {\mathcal {F}}:=\mathcal {F}_{\overline {S}}(\overline {\mathcal L})$
. Hence, Lemma 2.14 yields that
$\overline {\mathcal {F}}:=\mathcal {F}_{\overline {S}}(\overline {\mathcal L})$
. Hence, Lemma 2.14 yields that
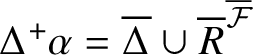 $\Delta ^+\alpha =\overline {\Delta }\cup \overline {R}^{\overline {\mathcal {F}}}$
, the subgroup
$\Delta ^+\alpha =\overline {\Delta }\cup \overline {R}^{\overline {\mathcal {F}}}$
, the subgroup
![]() $\overline {R}$
is fully
$\overline {R}$
is fully
![]() $\overline {\mathcal {F}}$
-normalised and
$\overline {\mathcal {F}}$
-normalised and
![]() $\alpha |_{N_S(R)}$
induces an epimorphism from
$\alpha |_{N_S(R)}$
induces an epimorphism from
![]() $N_{\mathcal {F}}(R)$
to
$N_{\mathcal {F}}(R)$
to
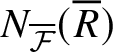 $N_{\overline {\mathcal {F}}}(\overline {R})$
. The latter fact implies that
$N_{\overline {\mathcal {F}}}(\overline {R})$
. The latter fact implies that
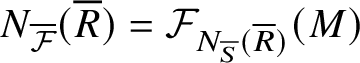 $N_{\overline {\mathcal {F}}}(\overline {R})=\mathcal {F}_{N_{\overline {S}}(\overline {R})}(M)$
. By Lemma 2.26,
$N_{\overline {\mathcal {F}}}(\overline {R})=\mathcal {F}_{N_{\overline {S}}(\overline {R})}(M)$
. By Lemma 2.26,
![]() $R^*:=O_p(N_{\mathcal L^+}(R))\in \Delta $
and
$R^*:=O_p(N_{\mathcal L^+}(R))\in \Delta $
and
![]() $R^*\unlhd N_{\mathcal L}(R)$
. Hence, setting
$R^*\unlhd N_{\mathcal L}(R)$
. Hence, setting
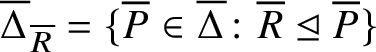 $\overline {\Delta }_{\overline {R}}=\{\overline {P}\in \overline {\Delta }\colon \overline {R}\unlhd \overline {P}\}$
, we have
$\overline {\Delta }_{\overline {R}}=\{\overline {P}\in \overline {\Delta }\colon \overline {R}\unlhd \overline {P}\}$
, we have
 $\overline {R^*}\in \overline {\Delta }_{\overline {R}}$
and
$\overline {R^*}\in \overline {\Delta }_{\overline {R}}$
and
![]() $\overline {R^*}\unlhd M$
, which implies
$\overline {R^*}\unlhd M$
, which implies
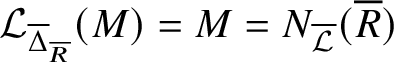 $\mathcal L_{\overline {\Delta }_{\overline {R}}}(M)=M=N_{\overline {\mathcal L}}(\overline {R})$
. Now [Reference Chermak6, Hypothesis 5.3] holds with
$\mathcal L_{\overline {\Delta }_{\overline {R}}}(M)=M=N_{\overline {\mathcal L}}(\overline {R})$
. Now [Reference Chermak6, Hypothesis 5.3] holds with
![]() $\overline {\mathcal {F}}$
,
$\overline {\mathcal {F}}$
,
![]() $(\overline {\mathcal L},\overline {\Delta },\overline {S})$
,
$(\overline {\mathcal L},\overline {\Delta },\overline {S})$
,
![]() $\overline {R}$
and
$\overline {R}$
and
![]() $\operatorname {id}_M$
in place of
$\operatorname {id}_M$
in place of
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $(\mathcal L,\Delta ,S)$
, T and
$(\mathcal L,\Delta ,S)$
, T and
![]() $\lambda $
. So by [Reference Chermak6, Theorem 5.14], setting
$\lambda $
. So by [Reference Chermak6, Theorem 5.14], setting
![]() $\widetilde {\Delta }:=\Delta ^+\alpha $
, there exists a locality
$\widetilde {\Delta }:=\Delta ^+\alpha $
, there exists a locality
![]() $({\widetilde {\mathcal {L}}},\widetilde {\Delta },\overline {S})$
such that
$({\widetilde {\mathcal {L}}},\widetilde {\Delta },\overline {S})$
such that
![]() $\overline {\mathcal L}\subseteq {\widetilde {\mathcal {L}}}$
,
$\overline {\mathcal L}\subseteq {\widetilde {\mathcal {L}}}$
,
![]() $N_{{\widetilde {\mathcal {L}}}}(R)=M$
, and the inclusion map
$N_{{\widetilde {\mathcal {L}}}}(R)=M$
, and the inclusion map
![]() $\overline {\mathcal L}\hookrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups. Hence,
$\overline {\mathcal L}\hookrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups. Hence,
![]() $\alpha $
regarded as a map
$\alpha $
regarded as a map
![]() $\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups, which by Corollary 3.3 extends to a homomorphism
$\mathcal L\longrightarrow {\widetilde {\mathcal {L}}}$
is a homomorphism of partial groups, which by Corollary 3.3 extends to a homomorphism
![]() $\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
of partial groups. Then
$\gamma \colon \mathcal L^+\longrightarrow {\widetilde {\mathcal {L}}}$
of partial groups. Then
![]() $\mathcal {N}^+:=\ker (\gamma )\unlhd \mathcal L^+$
and
$\mathcal {N}^+:=\ker (\gamma )\unlhd \mathcal L^+$
and
![]() $\mathcal {N}^+\cap \mathcal L=\ker (\alpha )=\mathcal {N}$
. This proves the assertion.
$\mathcal {N}^+\cap \mathcal L=\ker (\alpha )=\mathcal {N}$
. This proves the assertion.
Corollary 6.4. Let
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
be linking localities over the same fusion system
![]() $\mathcal {F}$
. Then
$\mathcal {F}$
. Then
![]() $|{\mathfrak {N}}(\mathcal L)|=|{\mathfrak {N}}(\mathcal L^+)|$
.
$|{\mathfrak {N}}(\mathcal L)|=|{\mathfrak {N}}(\mathcal L^+)|$
.
Proof. Suppose that
![]() $(\mathcal L,\Delta ,S)$
and
$(\mathcal L,\Delta ,S)$
and
![]() $(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
$(\mathcal L^+,\Delta ^+,S)$
are linking localities over the same fusion system
![]() $\mathcal {F}$
. By Proposition 3.3 and Theorem 7.2(a) in Reference Henke[14], there exist subcentric linking localities
$\mathcal {F}$
. By Proposition 3.3 and Theorem 7.2(a) in Reference Henke[14], there exist subcentric linking localities
![]() $(\hat {\mathcal L},\mathcal {F}^s,S)$
and
$(\hat {\mathcal L},\mathcal {F}^s,S)$
and
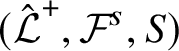 $(\hat {\mathcal L}^+,\mathcal {F}^s,S)$
over
$(\hat {\mathcal L}^+,\mathcal {F}^s,S)$
over
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\hat {\mathcal L}|_\Delta =\mathcal L$
and
$\hat {\mathcal L}|_\Delta =\mathcal L$
and
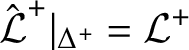 $\hat {\mathcal L}^+|_{\Delta ^+}=\mathcal L^+$
. Moreover, by [Reference Henke14, Theorem A(b)], there exists a rigid isomorphism
$\hat {\mathcal L}^+|_{\Delta ^+}=\mathcal L^+$
. Moreover, by [Reference Henke14, Theorem A(b)], there exists a rigid isomorphism
![]() $\alpha \colon \hat {\mathcal L}\longrightarrow \hat {\mathcal L}^+$
. Then
$\alpha \colon \hat {\mathcal L}\longrightarrow \hat {\mathcal L}^+$
. Then
![]() $\alpha $
induces a bijection
$\alpha $
induces a bijection
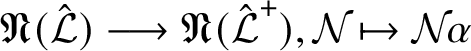 ${\mathfrak {N}}(\hat {\mathcal L})\longrightarrow {\mathfrak {N}}(\hat {\mathcal L}^+),\mathcal {N}\mapsto \mathcal {N}\alpha $
. So by Theorem C (applied twice), we have
${\mathfrak {N}}(\hat {\mathcal L})\longrightarrow {\mathfrak {N}}(\hat {\mathcal L}^+),\mathcal {N}\mapsto \mathcal {N}\alpha $
. So by Theorem C (applied twice), we have
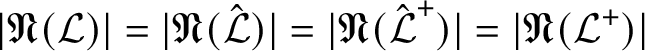 $|{\mathfrak {N}}(\mathcal L)|=|{\mathfrak {N}}(\hat {\mathcal L})|=|{\mathfrak {N}}(\hat {\mathcal L}^+)|=|{\mathfrak {N}}(\mathcal L^+)|$
. This shows the assertion.
$|{\mathfrak {N}}(\mathcal L)|=|{\mathfrak {N}}(\hat {\mathcal L})|=|{\mathfrak {N}}(\hat {\mathcal L}^+)|=|{\mathfrak {N}}(\mathcal L^+)|$
. This shows the assertion.
Acknowledgments
The author thanks the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support und hospitality during the programme groups, representations and applications, where work on this article was undertaken and supported by EPSRC Grant No. EP/R014604/1. Open Access Funding by the Publication Fund of the TU Dresden.
Conflicts of interest
None.