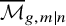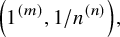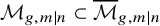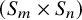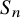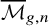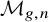1. Introduction
Given nonnegative integers g, m and n satisfying
set
![]() $\overline {\mathcal {M}}_{g,m|n}$
to be Hassett’s moduli space
$\overline {\mathcal {M}}_{g,m|n}$
to be Hassett’s moduli space
![]() $\overline {\mathcal {M}}_{g, \mathcal {A}}$
of weighted pointed stable curves of genus g, for the weight data
$\overline {\mathcal {M}}_{g, \mathcal {A}}$
of weighted pointed stable curves of genus g, for the weight data
 $$\begin{align*}\mathcal{A} =\left(\underbrace{1,\ldots, 1}_{m}, \underbrace{1/n, \ldots, 1/n}_{n} \right).\end{align*}$$
$$\begin{align*}\mathcal{A} =\left(\underbrace{1,\ldots, 1}_{m}, \underbrace{1/n, \ldots, 1/n}_{n} \right).\end{align*}$$
This space is a connected, smooth and proper Deligne-Mumford stack over
![]() $\mathbb {Z}$
, and is a compactification of the moduli space
$\mathbb {Z}$
, and is a compactification of the moduli space
![]() $\mathcal {M}_{g, m+n}$
of smooth pointed algebraic curves of genus g [Reference Hassett15]; this family of weight data has been called heavy/light in the literature [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Kannan, Karp and Li18]. We also set
$\mathcal {M}_{g, m+n}$
of smooth pointed algebraic curves of genus g [Reference Hassett15]; this family of weight data has been called heavy/light in the literature [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Kannan, Karp and Li18]. We also set
![]() $\mathcal {M}_{g, m|n} \subset \overline {\mathcal {M}}_{g, m|n}$
to be the locus of smooth, not necessarily distinctly marked curves. In this paper, we study the
$\mathcal {M}_{g, m|n} \subset \overline {\mathcal {M}}_{g, m|n}$
to be the locus of smooth, not necessarily distinctly marked curves. In this paper, we study the
![]() $(S_m \times S_n)$
-equivariant Hodge–Deligne polynomials of
$(S_m \times S_n)$
-equivariant Hodge–Deligne polynomials of
![]() $\mathcal {M}_{g, m|n}$
and
$\mathcal {M}_{g, m|n}$
and
![]() $\overline {\mathcal {M}}_{g, m|n}$
. Throughout this paper, we will work with the coarse moduli spaces of these stacks, as the mixed Hodge structure on the rational cohomology of a Deligne-Mumford stack coincides with that of its coarse moduli space.
$\overline {\mathcal {M}}_{g, m|n}$
. Throughout this paper, we will work with the coarse moduli spaces of these stacks, as the mixed Hodge structure on the rational cohomology of a Deligne-Mumford stack coincides with that of its coarse moduli space.
If X is a d-dimensional complex variety with an action of
![]() $S_m \times S_n$
, its complex cohomology groups are
$S_m \times S_n$
, its complex cohomology groups are
![]() $(S_m \times S_n)$
-representations in the category of mixed Hodge structures. The
$(S_m \times S_n)$
-representations in the category of mixed Hodge structures. The
![]() $(S_m \times S_n)$
-equivariant Hodge–Deligne polynomial of X is given by the formula
$(S_m \times S_n)$
-equivariant Hodge–Deligne polynomial of X is given by the formula
 $$ \begin{align} E_X^{S_m \times S_n}(u,v) := \sum_{i,p,q = 0}^{2d} (-1)^{i} \operatorname{ch}_{m,n}\left(\mathrm{Gr}^F_p\mathrm{Gr}^{W}_{p + q} H^{i}_c(X; \mathbb{C})\right) u^p v^q \in \Lambda^{(2)}[u,v], \end{align} $$
$$ \begin{align} E_X^{S_m \times S_n}(u,v) := \sum_{i,p,q = 0}^{2d} (-1)^{i} \operatorname{ch}_{m,n}\left(\mathrm{Gr}^F_p\mathrm{Gr}^{W}_{p + q} H^{i}_c(X; \mathbb{C})\right) u^p v^q \in \Lambda^{(2)}[u,v], \end{align} $$
where
![]() $\Lambda ^{(2)} = \Lambda \otimes \Lambda $
is the ring of bisymmetric functions,
$\Lambda ^{(2)} = \Lambda \otimes \Lambda $
is the ring of bisymmetric functions,
![]() $\operatorname {ch}_{m, n}(V) \in \Lambda ^{(2)}$
is the Frobenius characteristic of an
$\operatorname {ch}_{m, n}(V) \in \Lambda ^{(2)}$
is the Frobenius characteristic of an
![]() $(S_m \times S_n)$
-representation V, while W and F denote the weight and Hodge filtrations on the compactly supported cohomology of a complex algebraic variety, respectively. The Hodge–Deligne polynomial has also been referred to as the E-polynomial and the mixed Hodge polynomial in the literature. If X is proper, and the mixed Hodge structure on each cohomology group is pure, as is the case for the coarse moduli space of
$(S_m \times S_n)$
-representation V, while W and F denote the weight and Hodge filtrations on the compactly supported cohomology of a complex algebraic variety, respectively. The Hodge–Deligne polynomial has also been referred to as the E-polynomial and the mixed Hodge polynomial in the literature. If X is proper, and the mixed Hodge structure on each cohomology group is pure, as is the case for the coarse moduli space of
![]() $\overline {\mathcal {M}}_{g, m|n}$
, the Hodge–Deligne polynomial specializes to the usual Hodge polynomial
$\overline {\mathcal {M}}_{g, m|n}$
, the Hodge–Deligne polynomial specializes to the usual Hodge polynomial
 $$\begin{align*}\sum_{p,q = 0}^{2d} (-1)^{p+ q}\operatorname{ch}_{m, n}\left(H^{p,q}(X;\mathbb{C})\right) u^p v^q. \end{align*}$$
$$\begin{align*}\sum_{p,q = 0}^{2d} (-1)^{p+ q}\operatorname{ch}_{m, n}\left(H^{p,q}(X;\mathbb{C})\right) u^p v^q. \end{align*}$$
For more details on mixed Hodge structures, see [Reference Peters and Steenbrink28] or [Reference Chambert-Loir, Nicaise and Sebag8].
We assemble all of the equivariant Hodge–Deligne polynomials for heavy/light Hassett spaces with fixed genus into series with coefficients in
![]() $\Lambda ^{(2)}$
:
$\Lambda ^{(2)}$
:
We also define
In the above, for a variety X with action of
![]() $S_n$
, we have set
$S_n$
, we have set
![]() $E_{X}^{S_n}(u,v)$
for the
$E_{X}^{S_n}(u,v)$
for the
![]() $S_n$
-equivariant Hodge–Deligne polynomial of X, defined analogously to (1.1), replacing
$S_n$
-equivariant Hodge–Deligne polynomial of X, defined analogously to (1.1), replacing
![]() $\operatorname {ch}_{m,n}$
with the Frobenius characteristic
$\operatorname {ch}_{m,n}$
with the Frobenius characteristic
![]() $\operatorname {ch}_n$
of an
$\operatorname {ch}_n$
of an
![]() $S_n$
-representation, and replacing
$S_n$
-representation, and replacing
![]() $\Lambda ^{(2)}$
with
$\Lambda ^{(2)}$
with
![]() $\Lambda $
.
$\Lambda $
.
In order to state our main theorem on the above generating functions, we require some combinatorial preliminaries. Given a symmetric function
![]() $f \in \Lambda $
, we set
$f \in \Lambda $
, we set
![]() $f^{(j)} \in \Lambda ^{(2)}$
for the inclusion of f into the jth tensor factor,
$f^{(j)} \in \Lambda ^{(2)}$
for the inclusion of f into the jth tensor factor,
![]() $j\in \{1,2\}$
. These extend to maps
$j\in \{1,2\}$
. These extend to maps
![]() $\Lambda [[u,v]] \to \Lambda ^{(2)}[[u, v]]$
. Let
$\Lambda [[u,v]] \to \Lambda ^{(2)}[[u, v]]$
. Let
![]() $p_i \in \Lambda $
be the ith power sum symmetric function. The coproduct
$p_i \in \Lambda $
be the ith power sum symmetric function. The coproduct
![]() $\Lambda \to \Lambda ^{(2)}$
defined by
$\Lambda \to \Lambda ^{(2)}$
defined by
also extends to a map
![]() $\Delta : \Lambda [[u,v]] \to \Lambda ^{(2)}[[u,v]]$
. There are two plethysm operations
$\Delta : \Lambda [[u,v]] \to \Lambda ^{(2)}[[u,v]]$
. There are two plethysm operations
![]() $\circ _1, \circ _2$
defined on
$\circ _1, \circ _2$
defined on
![]() $\Lambda ^{(2)}$
, and these extend to
$\Lambda ^{(2)}$
, and these extend to
![]() $\Lambda ^{(2)}[[u, v]]$
by
$\Lambda ^{(2)}[[u, v]]$
by
 $$\begin{align*}p_n^{(i)} \circ_i q &= q^n,\\p_n^{(i)} \circ_j q &= p_n^{(i)}, \end{align*}$$
$$\begin{align*}p_n^{(i)} \circ_i q &= q^n,\\p_n^{(i)} \circ_j q &= p_n^{(i)}, \end{align*}$$
for
![]() $\{i,j\} = \{1,2\}$
and
$\{i,j\} = \{1,2\}$
and
![]() $q \in \{u, v\}$
. See Section 2.1 for more details and references on symmetric functions and the Frobenius characteristic.
$q \in \{u, v\}$
. See Section 2.1 for more details and references on symmetric functions and the Frobenius characteristic.
The main contributions of this paper are the following formulas, which encode the combinatorial relationships between the generating functions defined above.
Theorem A. Let
![]() $h_n \in \Lambda $
denote the nth homogeneous symmetric function. For
$h_n \in \Lambda $
denote the nth homogeneous symmetric function. For
![]() $f \in \Lambda [[u, v]]$
, set
$f \in \Lambda [[u, v]]$
, set
Then we have
and
 $$\begin{align*}\overline{\mathsf{a}}_g = \Delta(\overline{\mathsf{b}}_g) \circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1} \right)^{(2)} \circ_2 \operatorname{Exp}\left(p_1\right)^{(2)}. \end{align*}$$
$$\begin{align*}\overline{\mathsf{a}}_g = \Delta(\overline{\mathsf{b}}_g) \circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1} \right)^{(2)} \circ_2 \operatorname{Exp}\left(p_1\right)^{(2)}. \end{align*}$$
A formula for the series
![]() $\mathsf {b}_0$
has been given by Getzler [Reference Getzler10]; therefore, Theorem A determines
$\mathsf {b}_0$
has been given by Getzler [Reference Getzler10]; therefore, Theorem A determines
![]() $\mathsf {a}_g$
and
$\mathsf {a}_g$
and
![]() $\overline {\mathsf {a}}_g$
in terms of
$\overline {\mathsf {a}}_g$
in terms of
![]() $\mathsf {b}_g$
and
$\mathsf {b}_g$
and
![]() $\overline {\mathsf {b}}_g$
. Moreover, this transformation is invertible, as
$\overline {\mathsf {b}}_g$
. Moreover, this transformation is invertible, as
![]() $\operatorname {Exp}$
has a plethystic inverse
$\operatorname {Exp}$
has a plethystic inverse
![]() $\operatorname {Log}$
and
$\operatorname {Log}$
and
![]() $p_1 - \partial \mathsf {b}_0/\partial p_1$
is inverse to
$p_1 - \partial \mathsf {b}_0/\partial p_1$
is inverse to
![]() $p_1 + \partial \overline {\mathsf {b}}_0/\partial p_1$
. There is a numerical analogue of Theorem A which deals with the non-equivariant Hodge–Deligne polynomials, defined by the assignment
$p_1 + \partial \overline {\mathsf {b}}_0/\partial p_1$
. There is a numerical analogue of Theorem A which deals with the non-equivariant Hodge–Deligne polynomials, defined by the assignment
 $$\begin{align*}E_X(u, v) := \sum_{i,p,q = 0}^{2d} (-1)^{i} \dim\left(\mathrm{Gr}^F_p\mathrm{Gr}^{W}_{p + q} H^{i}_c(X; \mathbb{C})\right) u^p v^q \in \mathbb{Q}[u,v]. \end{align*}$$
$$\begin{align*}E_X(u, v) := \sum_{i,p,q = 0}^{2d} (-1)^{i} \dim\left(\mathrm{Gr}^F_p\mathrm{Gr}^{W}_{p + q} H^{i}_c(X; \mathbb{C})\right) u^p v^q \in \mathbb{Q}[u,v]. \end{align*}$$
Set
 $$\begin{align*}a_g := \sum_{m,n} E_{\mathcal{M}_{g, m|n}}(u, v) \frac{x^m y^n}{m! n!}, \quad \overline{a}_g := \sum_{m,n} E_{\overline{\mathcal{M}}_{g, m|n}}(u, v) \frac{x^m y^n}{m! n!} \in \mathbb{Q}[[u, v, x, y]], \end{align*}$$
$$\begin{align*}a_g := \sum_{m,n} E_{\mathcal{M}_{g, m|n}}(u, v) \frac{x^m y^n}{m! n!}, \quad \overline{a}_g := \sum_{m,n} E_{\overline{\mathcal{M}}_{g, m|n}}(u, v) \frac{x^m y^n}{m! n!} \in \mathbb{Q}[[u, v, x, y]], \end{align*}$$
and similarly, put
 $$\begin{align*}b_g := \sum_{n} E_{\mathcal{M}_{g, n}}(u, v) \frac{x^n}{n!}, \quad \overline{b}_g := \sum_{n} E_{\overline{\mathcal{M}}_{g, n}}(u, v) \frac{x^n}{n!} \in \mathbb{Q}[[u, v, x]]. \end{align*}$$
$$\begin{align*}b_g := \sum_{n} E_{\mathcal{M}_{g, n}}(u, v) \frac{x^n}{n!}, \quad \overline{b}_g := \sum_{n} E_{\overline{\mathcal{M}}_{g, n}}(u, v) \frac{x^n}{n!} \in \mathbb{Q}[[u, v, x]]. \end{align*}$$
Corollary B. We have
where
![]() $w =x + e^y - 1$
, and
$w =x + e^y - 1$
, and
where
Theorem A and Corollary B allow for many explicit computations. For example, Getzler [Reference Getzler12] gives a recursive formula for the calculation of
![]() $\overline {\mathsf {b}}_1$
, which allows us to compute
$\overline {\mathsf {b}}_1$
, which allows us to compute
![]() $\overline {\mathsf {a}}_1$
and
$\overline {\mathsf {a}}_1$
and
![]() $\overline {a}_1$
; sample calculations are included in Tables 1 and 2. Similarly, Chan et al. in [Reference Chan, Faber, Galatius and Payne5] give a formula for the
$\overline {a}_1$
; sample calculations are included in Tables 1 and 2. Similarly, Chan et al. in [Reference Chan, Faber, Galatius and Payne5] give a formula for the
![]() $S_n$
-equivariant weight 0 compactly supported Euler characteristic of
$S_n$
-equivariant weight 0 compactly supported Euler characteristic of
![]() $\mathcal {M}_{g, n}$
in arbitrary genus, so Theorem A gives a practical method to compute the
$\mathcal {M}_{g, n}$
in arbitrary genus, so Theorem A gives a practical method to compute the
![]() $(S_m \times S_n)$
-equivariant weight 0 compactly supported Euler characteristic of
$(S_m \times S_n)$
-equivariant weight 0 compactly supported Euler characteristic of
![]() $\mathcal {M}_{g, m|n}$
. Sample computations for
$\mathcal {M}_{g, m|n}$
. Sample computations for
![]() $g = 2$
have been included in Table 3.
$g = 2$
have been included in Table 3.
Table 1 The
![]() $(S_m \times S_n)$
-equivariant Poincare polynomials of
$(S_m \times S_n)$
-equivariant Poincare polynomials of
![]() $\overline {\mathcal {M}}_{1, m|n}$
for
$\overline {\mathcal {M}}_{1, m|n}$
for
![]() $m + n \leq 5$
. The omitted terms are determined by Poincaré duality.
$m + n \leq 5$
. The omitted terms are determined by Poincaré duality.

Table 2 The Hodge polynomial of
![]() $\overline {\mathcal {M}}_{1, 0|n}$
for
$\overline {\mathcal {M}}_{1, 0|n}$
for
![]() $n \leq 11$
.
$n \leq 11$
.

1.1. Context
The heavy/light moduli space
![]() $\overline {\mathcal {M}}_{g, m|n}$
has been studied in several algebro-geometric contexts. It is of interest in its own right, as a modular compactification of
$\overline {\mathcal {M}}_{g, m|n}$
has been studied in several algebro-geometric contexts. It is of interest in its own right, as a modular compactification of
![]() $\mathcal {M}_{g, m+n}$
which admits a birational morphism from the Deligne–Mumford–Knudsen moduli space
$\mathcal {M}_{g, m+n}$
which admits a birational morphism from the Deligne–Mumford–Knudsen moduli space
![]() $\overline {\mathcal {M}}_{g, m+n}$
. It may be viewed as a resolution of singularities of the n-fold product of the universal curve over
$\overline {\mathcal {M}}_{g, m+n}$
. It may be viewed as a resolution of singularities of the n-fold product of the universal curve over
![]() $\overline {\mathcal {M}}_{g, m}$
[Reference Janda17]. It arises in the theory of stable quotients [Reference Marian, Oprea and Pandharipande23] and in tropical geometry [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Möller, Ulirsch and Werner24, Reference Hahn and Li16]. As g, m and n vary, the spaces
$\overline {\mathcal {M}}_{g, m}$
[Reference Janda17]. It arises in the theory of stable quotients [Reference Marian, Oprea and Pandharipande23] and in tropical geometry [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Möller, Ulirsch and Werner24, Reference Hahn and Li16]. As g, m and n vary, the spaces
![]() $\overline {\mathcal {M}}_{g, m|n}$
form the components of Losev–Manin’s extended modular operad [Reference Losev and Manin21]; when
$\overline {\mathcal {M}}_{g, m|n}$
form the components of Losev–Manin’s extended modular operad [Reference Losev and Manin21]; when
![]() $g = 0$
and
$g = 0$
and
![]() $m = 2$
, the space
$m = 2$
, the space
![]() $\overline {\mathcal {M}}_{0, 2|n}$
is a toric variety, and it coincides with the Losev–Manin moduli space of stable chains of
$\overline {\mathcal {M}}_{0, 2|n}$
is a toric variety, and it coincides with the Losev–Manin moduli space of stable chains of
![]() $\mathbb {P}^1$
’s [Reference Losev and Manin20].
$\mathbb {P}^1$
’s [Reference Losev and Manin20].
Part of the motivation for our work is to generate new data on the symmetric group representations afforded by the cohomology of these moduli spaces, and to understand how changing the weight data affects the cohomological complexity. For example, our Corollary 5.2 shows that asymptotically, the all-light-points compactification
![]() $\overline {\mathcal {M}}_{1, 0|n}$
has significantly less cohomology than the Deligne–Mumford compactification
$\overline {\mathcal {M}}_{1, 0|n}$
has significantly less cohomology than the Deligne–Mumford compactification
![]() $\overline {\mathcal {M}}_{1, n}$
. We ask if the same phenomenon holds in higher genus (Question 5.3). In hopes that our data will help others prove new theorems about the cohomology of these moduli spaces, we also ask (Question 5.4) whether one can find a closed formula for the equivariant weight zero compactly supported Euler characteristics of the open moduli spaces
$\overline {\mathcal {M}}_{1, n}$
. We ask if the same phenomenon holds in higher genus (Question 5.3). In hopes that our data will help others prove new theorems about the cohomology of these moduli spaces, we also ask (Question 5.4) whether one can find a closed formula for the equivariant weight zero compactly supported Euler characteristics of the open moduli spaces
![]() $\mathcal {M}_{g, m|n}$
, as is done for
$\mathcal {M}_{g, m|n}$
, as is done for
![]() $\mathcal {M}_{g, n}$
in [Reference Chan, Faber, Galatius and Payne5]. Our theorem in principle allows one to calculate these Euler characteristics for arbitrary g, m and n, but as our formulas involve plethysm, this is a very difficult computational task.
$\mathcal {M}_{g, n}$
in [Reference Chan, Faber, Galatius and Payne5]. Our theorem in principle allows one to calculate these Euler characteristics for arbitrary g, m and n, but as our formulas involve plethysm, this is a very difficult computational task.
Table 3 The
![]() $(S_m \times S_n)$
-equivariant and numerical weight zero compactly supported Euler characteristics of
$(S_m \times S_n)$
-equivariant and numerical weight zero compactly supported Euler characteristics of
![]() $\mathcal {M}_{2, m|n}$
.
$\mathcal {M}_{2, m|n}$
.

1.2. Related work
The first part of Corollary B follows from an observation made in [Reference Kannan, Li, Serpente and Yun19]: that in the Grothendieck ring of varieties, one has an equality
 $$\begin{align*}[\mathcal{M}_{g, m|n} ] = \sum_{k = 1}^{n} S(n, k) [\mathcal{M}_{g, m + k}], \end{align*}$$
$$\begin{align*}[\mathcal{M}_{g, m|n} ] = \sum_{k = 1}^{n} S(n, k) [\mathcal{M}_{g, m + k}], \end{align*}$$
where
![]() $S(n, k)$
, the Stirling number of the second kind, counts the number of partitions of
$S(n, k)$
, the Stirling number of the second kind, counts the number of partitions of
![]() $\{1, \ldots , n\}$
with k parts. It follows that the generating function
$\{1, \ldots , n\}$
with k parts. It follows that the generating function
![]() $a_g$
can be obtained from
$a_g$
can be obtained from
![]() $b_g(x + t)$
by making the substitution
$b_g(x + t)$
by making the substitution
![]() $t = e^{y} - 1$
; this transformation is called the Stirling transform. Both parts of Theorem A involve plethysm with the symmetric function
$t = e^{y} - 1$
; this transformation is called the Stirling transform. Both parts of Theorem A involve plethysm with the symmetric function
![]() $\operatorname {Exp}(p_1)^{(2)}$
, which transforms to
$\operatorname {Exp}(p_1)^{(2)}$
, which transforms to
![]() $e^{y} - 1$
under the rank homomorphism
$e^{y} - 1$
under the rank homomorphism
![]() $\Lambda \otimes \Lambda \to \mathbb {Q}[[x, y]]$
. Thus, Theorem A can be viewed as an application of the equivariant version of the Stirling transform.
$\Lambda \otimes \Lambda \to \mathbb {Q}[[x, y]]$
. Thus, Theorem A can be viewed as an application of the equivariant version of the Stirling transform.
In genus zero, the problem of computing the equivariant Hodge polynomials of
![]() $\overline {\mathcal {M}}_{0, m|n}$
has been studied by Bergström–Minabe [Reference Bergström and Minabe2, Reference Bergström and Minabe3] and by Chaudhuri [Reference Chaudhuri6]. Our formula gives a third approach to this problem, which applies in arbitrary genus.
$\overline {\mathcal {M}}_{0, m|n}$
has been studied by Bergström–Minabe [Reference Bergström and Minabe2, Reference Bergström and Minabe3] and by Chaudhuri [Reference Chaudhuri6]. Our formula gives a third approach to this problem, which applies in arbitrary genus.
Also in genus zero, the Chow groups of
![]() $\overline {\mathcal {M}}_{0, m|n}$
have been computed by Ceyhan [Reference Ceyhan4]. The Chow ring has been computed by Petersen [Reference Petersen27] and by Kannan–Karp–Li [Reference Kannan, Karp and Li18]. Our combinatorial proofs of plethystic formulas are similar to those in Petersen’s work [Reference Petersen26, §4] on moduli spaces of genus two curves of compact type, and their tautological rings.
$\overline {\mathcal {M}}_{0, m|n}$
have been computed by Ceyhan [Reference Ceyhan4]. The Chow ring has been computed by Petersen [Reference Petersen27] and by Kannan–Karp–Li [Reference Kannan, Karp and Li18]. Our combinatorial proofs of plethystic formulas are similar to those in Petersen’s work [Reference Petersen26, §4] on moduli spaces of genus two curves of compact type, and their tautological rings.
The techniques of this paper are based on prior work on the operad structure of moduli of stable curves and maps, by Getzler [Reference Getzler10, Reference Getzler12], Getzler–Kapranov [Reference Getzler and Kapranov13] and Getzler–Pandharipande [Reference Getzler and Pandharipande14]. In particular, the main tools of the paper are Getzler–Pandharipande’s theory of
![]() $\mathbb {S}$
-spaces, which encode sequences of varieties with
$\mathbb {S}$
-spaces, which encode sequences of varieties with
![]() $S_n$
-actions, together with a careful analysis of permutation group actions on the boundary strata of the spaces
$S_n$
-actions, together with a careful analysis of permutation group actions on the boundary strata of the spaces
![]() $\overline {\mathcal {M}}_{g, m|n}$
. To carry this out, we use the language of
$\overline {\mathcal {M}}_{g, m|n}$
. To carry this out, we use the language of
![]() $\mathbb {S}^2$
-spaces, which are a mild generalization of Getzler–Pandharipande’s theory. In this way, our approach is similar to that of Chaudhuri [Reference Chaudhuri6], who uses the language of
$\mathbb {S}^2$
-spaces, which are a mild generalization of Getzler–Pandharipande’s theory. In this way, our approach is similar to that of Chaudhuri [Reference Chaudhuri6], who uses the language of
![]() $\mathbb {S}^2$
-modules. To understand the cohomology of the open moduli space with its mixed Hodge structure, Chaudhuri uses the Leray spectral sequence associated to the fibration
$\mathbb {S}^2$
-modules. To understand the cohomology of the open moduli space with its mixed Hodge structure, Chaudhuri uses the Leray spectral sequence associated to the fibration
![]() $\mathcal {M}_{0, m|n} \to \mathcal {M}_{0, m|n-1}$
. However, this technique seems to be limited to the genus zero case. We restrict ourselves to the study of the Hodge–Deligne polynomial of
$\mathcal {M}_{0, m|n} \to \mathcal {M}_{0, m|n-1}$
. However, this technique seems to be limited to the genus zero case. We restrict ourselves to the study of the Hodge–Deligne polynomial of
![]() $\mathcal {M}_{g, m|n}$
, which contains less information than the full cohomology ring with its mixed Hodge structure.
$\mathcal {M}_{g, m|n}$
, which contains less information than the full cohomology ring with its mixed Hodge structure.
1.3. Outline of the paper
We review the necessary background on symmetric functions, the Frobenius characteristic and Hassett spaces in Section 2. In Section 3, we define the Grothendieck ring of
![]() $\mathbb {S}^2$
-spaces and its composition operations as categorifications of plethysm. We then use these composition operations to prove Theorem A in Section 4. Explicit calculations and accompanying remarks are included at the end of the paper, in Section 5.
$\mathbb {S}^2$
-spaces and its composition operations as categorifications of plethysm. We then use these composition operations to prove Theorem A in Section 4. Explicit calculations and accompanying remarks are included at the end of the paper, in Section 5.
2. Background
Here we briefly recall some background on symmetric functions and on Hassett spaces.
2.1. Symmetric functions and the Frobenius characteristic
For a more detailed background on the ring of symmetric functions, see Macdonald [Reference Macdonald22], Stanley [Reference Stanley29] or Getzler–Kapranov [Reference Getzler and Kapranov13, §7]. The ring
![]() $\Lambda $
of symmetric functions over
$\Lambda $
of symmetric functions over
![]() $\mathbb {Q}$
is defined as
$\mathbb {Q}$
is defined as
Elements of
![]() $\Lambda $
are power series which are invariant under any permutation of the variables. We have that
$\Lambda $
are power series which are invariant under any permutation of the variables. We have that
where
![]() $p_i = \sum _{k> 0} x_k^i$
is the ith power sum symmetric function. The ring
$p_i = \sum _{k> 0} x_k^i$
is the ith power sum symmetric function. The ring
![]() $\Lambda $
is graded by degree, and
$\Lambda $
is graded by degree, and
![]() $p_i$
has degree i. One can view
$p_i$
has degree i. One can view
![]() $\Lambda $
as the Grothendieck ring of
$\Lambda $
as the Grothendieck ring of
![]() $\mathbb {S}$
-modules, where an
$\mathbb {S}$
-modules, where an
![]() $\mathbb {S}$
-module
$\mathbb {S}$
-module
![]() $\mathcal {V}$
is the data of an
$\mathcal {V}$
is the data of an
![]() $S_n$
-representation
$S_n$
-representation
![]() $\mathcal {V}(n)$
for each
$\mathcal {V}(n)$
for each
![]() $n \geq 0$
. The ring structure on the Grothendieck ring of
$n \geq 0$
. The ring structure on the Grothendieck ring of
![]() $\mathbb {S}$
-modules is induced by the tensor product:
$\mathbb {S}$
-modules is induced by the tensor product:
 $$\begin{align*}(\mathcal{V} \otimes \mathcal{W})(n) = \bigoplus_{j = 0}^{n} \operatorname{Ind}_{S_j \times S_{n - j}}^{S_n} \mathcal{V}(j) \otimes \mathcal{W}(n-j), \end{align*}$$
$$\begin{align*}(\mathcal{V} \otimes \mathcal{W})(n) = \bigoplus_{j = 0}^{n} \operatorname{Ind}_{S_j \times S_{n - j}}^{S_n} \mathcal{V}(j) \otimes \mathcal{W}(n-j), \end{align*}$$
where
![]() $\operatorname {Ind}$
denotes induction of representations. Given an
$\operatorname {Ind}$
denotes induction of representations. Given an
![]() $\mathbb {S}$
-module
$\mathbb {S}$
-module
![]() $\mathcal {V}$
, the Frobenius characteristic
$\mathcal {V}$
, the Frobenius characteristic
![]() $\operatorname {ch}(\mathcal {V})$
is defined by
$\operatorname {ch}(\mathcal {V})$
is defined by
where for an
![]() $S_n$
-representation V, we have
$S_n$
-representation V, we have
 $$\begin{align*}\operatorname{ch}_n(V) := \frac{1}{n!} \sum_{\sigma \in S_n} \mathrm{Tr}_V(\sigma) p_{\lambda(\sigma)}, \end{align*}$$
$$\begin{align*}\operatorname{ch}_n(V) := \frac{1}{n!} \sum_{\sigma \in S_n} \mathrm{Tr}_V(\sigma) p_{\lambda(\sigma)}, \end{align*}$$
where
![]() $\lambda (\sigma )$
is the cycle type of the permutation
$\lambda (\sigma )$
is the cycle type of the permutation
![]() $\sigma $
, and for a partition
$\sigma $
, and for a partition
![]() $\lambda \vdash n$
, we set
$\lambda \vdash n$
, we set
![]() $p_\lambda := \prod _{i} p_{\lambda _i}$
. The Frobenius characteristic induces a ring isomorphism
$p_\lambda := \prod _{i} p_{\lambda _i}$
. The Frobenius characteristic induces a ring isomorphism
where
![]() $K_0(\mathbb {S}\text {-modules})$
is the aforementioned Grothendieck ring of
$K_0(\mathbb {S}\text {-modules})$
is the aforementioned Grothendieck ring of
![]() $\mathbb {S}$
-modules. In particular, if V is an
$\mathbb {S}$
-modules. In particular, if V is an
![]() $S_n$
-representation, then
$S_n$
-representation, then
![]() $\operatorname {ch}_n(V)$
determines V: the Schur functions
$\operatorname {ch}_n(V)$
determines V: the Schur functions
![]() $s_{\lambda }$
for
$s_{\lambda }$
for
![]() $\lambda \vdash n$
form a basis for the homogeneous degree n part of
$\lambda \vdash n$
form a basis for the homogeneous degree n part of
![]() $\Lambda $
, and if
$\Lambda $
, and if
is the decomposition of V into Specht modules, then
We define the homogeneous symmetric functions
![]() $h_n$
by
$h_n$
by
where
![]() $\mathrm {Triv}_n$
is the trivial
$\mathrm {Triv}_n$
is the trivial
![]() $S_n$
-representation of dimension one. Note that
$S_n$
-representation of dimension one. Note that
![]() $h_n = s_n$
.
$h_n = s_n$
.
There is an associative operation
![]() $\circ $
, called plethysm, on
$\circ $
, called plethysm, on
![]() $\Lambda $
. The plethysm
$\Lambda $
. The plethysm
![]() $f \circ g$
is defined when f has bounded degree, or when the degree
$f \circ g$
is defined when f has bounded degree, or when the degree
![]() $0$
term of g vanishes. It is characterized by the following formulas:
$0$
term of g vanishes. It is characterized by the following formulas:
-
(i)
 $(f_1 + f_2) \circ g = f_1 \circ g + f_2 \circ g$
,
$(f_1 + f_2) \circ g = f_1 \circ g + f_2 \circ g$
, -
(ii)
 $(f_1 f_2) \circ g = (f_1 \circ g)(f_2 \circ g)$
,
$(f_1 f_2) \circ g = (f_1 \circ g)(f_2 \circ g)$
, -
(iii) if
 $f = f(p_1, p_2, \ldots )$
, then
$f = f(p_1, p_2, \ldots )$
, then
 $p_n \circ f = f(p_n, p_{2n}, \ldots )$
.
$p_n \circ f = f(p_n, p_{2n}, \ldots )$
.
Plethysm has an interpretation on the level of Frobenius characteristics: given two
![]() $\mathbb {S}$
-modules
$\mathbb {S}$
-modules
![]() $\mathcal {V}$
and
$\mathcal {V}$
and
![]() $\mathcal {W}$
with
$\mathcal {W}$
with
![]() $\mathcal {W}(0) = 0$
, define a third
$\mathcal {W}(0) = 0$
, define a third
![]() $\mathbb {S}$
-module
$\mathbb {S}$
-module
![]() $\mathcal {V} \circ \mathcal {W}$
by the formula
$\mathcal {V} \circ \mathcal {W}$
by the formula
 $$\begin{align*}(\mathcal{V} \circ \mathcal{W})(n) := \bigoplus_{j \geq 0} \mathcal{V}(j) \otimes_{S_j} \mathcal{W}^{\otimes j}(n). \end{align*}$$
$$\begin{align*}(\mathcal{V} \circ \mathcal{W})(n) := \bigoplus_{j \geq 0} \mathcal{V}(j) \otimes_{S_j} \mathcal{W}^{\otimes j}(n). \end{align*}$$
Then
![]() $\operatorname {ch}(\mathcal {V} \circ \mathcal {W}) = \operatorname {ch}(\mathcal {V}) \circ \operatorname {ch}(\mathcal {W})$
; see [Reference Getzler and Kapranov13, Proposition 7.3] or [Reference Stanley29, Chapter 7, Appendix 2].
$\operatorname {ch}(\mathcal {V} \circ \mathcal {W}) = \operatorname {ch}(\mathcal {V}) \circ \operatorname {ch}(\mathcal {W})$
; see [Reference Getzler and Kapranov13, Proposition 7.3] or [Reference Stanley29, Chapter 7, Appendix 2].
All of these constructions generalize to
![]() $(S_m \times S_n)$
-representations. As in the introduction, we set
$(S_m \times S_n)$
-representations. As in the introduction, we set
we call
![]() $\Lambda ^{(2)}$
the ring of bisymmetric functions. Given
$\Lambda ^{(2)}$
the ring of bisymmetric functions. Given
![]() $f \in \Lambda $
, we write
$f \in \Lambda $
, we write
![]() $f^{(j)}$
for the inclusion of f into the jth tensor factor. Then we have
$f^{(j)}$
for the inclusion of f into the jth tensor factor. Then we have
Define an
![]() $\mathbb {S}^2$
-module
$\mathbb {S}^2$
-module
![]() $\mathcal {V}$
to be the data of an
$\mathcal {V}$
to be the data of an
![]() $(S_m \times S_n)$
-representation
$(S_m \times S_n)$
-representation
![]() $\mathcal {V}(m, n)$
for each
$\mathcal {V}(m, n)$
for each
![]() $m, n \geq 0$
. Given an
$m, n \geq 0$
. Given an
![]() $(S_{m} \times S_n)$
-representation V, its Frobenius characteristic is the bisymmetric function
$(S_{m} \times S_n)$
-representation V, its Frobenius characteristic is the bisymmetric function
 $$\begin{align*}\operatorname{ch}_{m,n}(V) := \frac{1}{m!\cdot n!} \sum_{(\sigma, \tau) \in S_{m} \times S_n} \mathrm{Tr}_V(\sigma, \tau) p^{(1)}_{\lambda(\sigma)} p^{(2)}_{\lambda(\tau)}. \end{align*}$$
$$\begin{align*}\operatorname{ch}_{m,n}(V) := \frac{1}{m!\cdot n!} \sum_{(\sigma, \tau) \in S_{m} \times S_n} \mathrm{Tr}_V(\sigma, \tau) p^{(1)}_{\lambda(\sigma)} p^{(2)}_{\lambda(\tau)}. \end{align*}$$
Just as in the single variable case, the bisymmetric function
![]() $\operatorname {ch}_{m,n}(V)$
completely determines the
$\operatorname {ch}_{m,n}(V)$
completely determines the
![]() $(S_m \times S_n)$
-representation V: if
$(S_m \times S_n)$
-representation V: if
 $$\begin{align*}V = \bigoplus_{\substack{{\lambda \vdash m}\\{\mu \vdash n}}} \left(W_{\lambda} \otimes W_{\mu} \right)^{\oplus a_{\lambda \mu}}, \end{align*}$$
$$\begin{align*}V = \bigoplus_{\substack{{\lambda \vdash m}\\{\mu \vdash n}}} \left(W_{\lambda} \otimes W_{\mu} \right)^{\oplus a_{\lambda \mu}}, \end{align*}$$
then
 $$\begin{align*}\operatorname{ch}_{m,n}(V) = \sum_{\lambda, \mu} a_{\lambda \mu} s_{\lambda}^{(1)} s_{\mu}^{(2)}. \end{align*}$$
$$\begin{align*}\operatorname{ch}_{m,n}(V) = \sum_{\lambda, \mu} a_{\lambda \mu} s_{\lambda}^{(1)} s_{\mu}^{(2)}. \end{align*}$$
The Frobenius characteristic of a
![]() $\mathbb {S}^2$
-module
$\mathbb {S}^2$
-module
![]() $\mathcal {V}$
is defined by
$\mathcal {V}$
is defined by
It furnishes a ring isomorphism from the Grothendieck ring of
![]() $\mathbb {S}^2$
-modules to
$\mathbb {S}^2$
-modules to
![]() $\Lambda ^{(2)}$
. The ring
$\Lambda ^{(2)}$
. The ring
![]() $\Lambda ^{(2)}$
has two plethysm operations
$\Lambda ^{(2)}$
has two plethysm operations
![]() $\circ _1$
and
$\circ _1$
and
![]() $\circ _2$
; the operation
$\circ _2$
; the operation
![]() $f \circ _i g$
is defined whenever f has bounded degree, or the degree
$f \circ _i g$
is defined whenever f has bounded degree, or the degree
![]() $(0,0)$
term of g vanishes. These operations are characterized by
$(0,0)$
term of g vanishes. These operations are characterized by
-
(i)
 $(f_1 + f_2) \circ _i g = f_1 \circ _i g + f_2 \circ _i g$
,
$(f_1 + f_2) \circ _i g = f_1 \circ _i g + f_2 \circ _i g$
, -
(ii)
 $(f_1 f_2) \circ _i g = (f_1 \circ _i g)(f_2 \circ _i g)$
,
$(f_1 f_2) \circ _i g = (f_1 \circ _i g)(f_2 \circ _i g)$
, -
(iii) if
 $f = f(p_1^{(1)}, p_1^{(2)}, p_2^{(1)}, p_2^{(2)} \ldots )$
, then
$f = f(p_1^{(1)}, p_1^{(2)}, p_2^{(1)}, p_2^{(2)} \ldots )$
, then
 $p_n^{(i)} \circ _i f = f(p_n^{(1)}, p_n^{(2)}, p_{2n}^{(1)}, p_{2n}^{(2)}, \ldots )$
, for any
$p_n^{(i)} \circ _i f = f(p_n^{(1)}, p_n^{(2)}, p_{2n}^{(1)}, p_{2n}^{(2)}, \ldots )$
, for any
 $i, j \in \{1,2\}$
, and
$i, j \in \{1,2\}$
, and -
(iv)
 $p_n^{(i)} \circ _j f = p_n^{(i)}$
if
$p_n^{(i)} \circ _j f = p_n^{(i)}$
if
 $i \neq j$
;
$i \neq j$
;
see Chaudhuri [Reference Chaudhuri6]. We will make use of the following interpretation of plethysm, for which we are not aware of a suitable reference in the bisymmetric case. Let
![]() $\mathcal {V}$
be an
$\mathcal {V}$
be an
![]() $\mathbb {S}^2$
-module, and let
$\mathbb {S}^2$
-module, and let
![]() $\mathcal {W}$
be an
$\mathcal {W}$
be an
![]() $\mathbb {S}$
-module with
$\mathbb {S}$
-module with
![]() $\mathcal {W}(0) = 0$
. We can compose these in two ways to get an
$\mathcal {W}(0) = 0$
. We can compose these in two ways to get an
![]() $\mathbb {S}^2$
-module:
$\mathbb {S}^2$
-module:
 $$ \begin{align*} (\mathcal{V} \circ_1 \mathcal{W})(m, n) &= \bigoplus_{j \geq 0} \mathcal{V}(j, n) \otimes_{S_j} \mathcal{W}^{\otimes j}(m)\\ (\mathcal{V} \circ_2 \mathcal{W})(m, n) &= \bigoplus_{j \geq 0} \mathcal{V}(m, j) \otimes_{S_j} \mathcal{W}^{\otimes j}(n). \end{align*} $$
$$ \begin{align*} (\mathcal{V} \circ_1 \mathcal{W})(m, n) &= \bigoplus_{j \geq 0} \mathcal{V}(j, n) \otimes_{S_j} \mathcal{W}^{\otimes j}(m)\\ (\mathcal{V} \circ_2 \mathcal{W})(m, n) &= \bigoplus_{j \geq 0} \mathcal{V}(m, j) \otimes_{S_j} \mathcal{W}^{\otimes j}(n). \end{align*} $$
We will interpret plethysm of bisymmetric functions in terms of these composition operations.
Proposition 2.1. Let
![]() $\mathcal {V}$
be an
$\mathcal {V}$
be an
![]() $\mathbb {S}^2$
-module, and let
$\mathbb {S}^2$
-module, and let
![]() $\mathcal {W}$
be an
$\mathcal {W}$
be an
![]() $\mathbb {S}$
-module. Then
$\mathbb {S}$
-module. Then
and
Proof. Since
it suffices to consider the case where
![]() $\mathcal {V}$
is supported in a single degree
$\mathcal {V}$
is supported in a single degree
![]() $(m, k)$
and
$(m, k)$
and
![]() $\mathcal {V}(m, k)$
is irreducible, so that
$\mathcal {V}(m, k)$
is irreducible, so that
![]() $\mathcal {V}(m, k) \cong V_\lambda \otimes V_\mu $
, where
$\mathcal {V}(m, k) \cong V_\lambda \otimes V_\mu $
, where
![]() $\lambda \vdash n$
,
$\lambda \vdash n$
,
![]() $\mu \vdash k$
and
$\mu \vdash k$
and
![]() $V_\lambda , V_\mu $
are the respective Specht modules. We will also suppose that
$V_\lambda , V_\mu $
are the respective Specht modules. We will also suppose that
![]() $i = 2$
. In this case, we have
$i = 2$
. In this case, we have
 $$ \begin{align*} (\mathcal{V} \circ_2 \mathcal{W})(m, n) &= \mathcal{V}(m, k) \otimes_{S_k} \mathcal{W}^{\otimes k}(n) \\&\cong (V_\lambda \otimes V_\mu) \otimes_{S_k} \mathcal{W}^{\otimes k}(n) \\&\cong V_\lambda \otimes (V_\mu \otimes_{S_k} \mathcal{W}^{\otimes k}(n)) \\&\cong V_\lambda \otimes (V_\mu \circ \mathcal{W})(n). \end{align*} $$
$$ \begin{align*} (\mathcal{V} \circ_2 \mathcal{W})(m, n) &= \mathcal{V}(m, k) \otimes_{S_k} \mathcal{W}^{\otimes k}(n) \\&\cong (V_\lambda \otimes V_\mu) \otimes_{S_k} \mathcal{W}^{\otimes k}(n) \\&\cong V_\lambda \otimes (V_\mu \otimes_{S_k} \mathcal{W}^{\otimes k}(n)) \\&\cong V_\lambda \otimes (V_\mu \circ \mathcal{W})(n). \end{align*} $$
Taking
![]() $\operatorname {ch}$
on both sides, we see that
$\operatorname {ch}$
on both sides, we see that
 $$ \begin{align*} \operatorname{ch}(\mathcal{V} \circ_2 \mathcal{W}) &= \operatorname{ch}(V_\lambda) \otimes \operatorname{ch} (V_\mu \circ \mathcal{W}) \\&= \operatorname{ch}(V_\lambda) \otimes (\operatorname{ch} (V_\mu) \circ \operatorname{ch}(\mathcal{W})) \\&= \left(\operatorname{ch}(V_\lambda) \otimes \operatorname{ch}(V_\mu)\right) \circ_2 1 \otimes \operatorname{ch}(\mathcal{W}) \\&= \operatorname{ch}(\mathcal{V}) \circ_2 (1 \otimes \operatorname{ch}(\mathcal{W})); \end{align*} $$
$$ \begin{align*} \operatorname{ch}(\mathcal{V} \circ_2 \mathcal{W}) &= \operatorname{ch}(V_\lambda) \otimes \operatorname{ch} (V_\mu \circ \mathcal{W}) \\&= \operatorname{ch}(V_\lambda) \otimes (\operatorname{ch} (V_\mu) \circ \operatorname{ch}(\mathcal{W})) \\&= \left(\operatorname{ch}(V_\lambda) \otimes \operatorname{ch}(V_\mu)\right) \circ_2 1 \otimes \operatorname{ch}(\mathcal{W}) \\&= \operatorname{ch}(\mathcal{V}) \circ_2 (1 \otimes \operatorname{ch}(\mathcal{W})); \end{align*} $$
the case of the operation
![]() $\circ _1$
is similar.
$\circ _1$
is similar.
The ring
![]() $\Lambda $
is a Hopf algebra, with coproduct
$\Lambda $
is a Hopf algebra, with coproduct
![]() $\Delta : \Lambda \to \Lambda ^{(2)}$
defined by
$\Delta : \Lambda \to \Lambda ^{(2)}$
defined by
On the level of Frobenius characteristic, we have
 $$ \begin{align} \Delta(\operatorname{ch}_n(V)) = \sum_{k = 0}^{n} \operatorname{ch}_{k, n-k}\left(\operatorname{Res}^{S_n}_{S_{k} \times S_{n - k}} V\right), \end{align} $$
$$ \begin{align} \Delta(\operatorname{ch}_n(V)) = \sum_{k = 0}^{n} \operatorname{ch}_{k, n-k}\left(\operatorname{Res}^{S_n}_{S_{k} \times S_{n - k}} V\right), \end{align} $$
where
![]() $\operatorname {Res}$
denotes restriction of representations. There is a rank homomorphism
$\operatorname {Res}$
denotes restriction of representations. There is a rank homomorphism
determined by
or equivalently,
![]() $p_1 \mapsto x$
and
$p_1 \mapsto x$
and
![]() $p_n \mapsto 0$
for
$p_n \mapsto 0$
for
![]() $n> 1$
. This takes plethysm into composition of power series. We use the same notation for the morphism
$n> 1$
. This takes plethysm into composition of power series. We use the same notation for the morphism
determined by
or
![]() $p_1^{(1)} \mapsto x$
,
$p_1^{(1)} \mapsto x$
,
![]() $p_1^{(2)} \mapsto y$
and
$p_1^{(2)} \mapsto y$
and
![]() $p_n^{(j)} \mapsto 0$
for
$p_n^{(j)} \mapsto 0$
for
![]() $n> 1$
. In this case, the two plethysm operations
$n> 1$
. In this case, the two plethysm operations
![]() $\circ _1$
and
$\circ _1$
and
![]() $\circ _2$
are carried into composition in x and y, respectively.
$\circ _2$
are carried into composition in x and y, respectively.
2.2. Hassett spaces
Let
![]() $g\geq 0$
,
$g\geq 0$
,
![]() $n \geq 1$
be two integers, and let
$n \geq 1$
be two integers, and let
![]() $\mathcal {A} =(a_1 ,\dots , a_n )\in ((0,1]\cap \mathbb {Q})^n$
be a weight datum such that
$\mathcal {A} =(a_1 ,\dots , a_n )\in ((0,1]\cap \mathbb {Q})^n$
be a weight datum such that
![]() $2g-2 + a_1 +\dots +a_n>0.$
Let C be a curve, at worst nodal, with
$2g-2 + a_1 +\dots +a_n>0.$
Let C be a curve, at worst nodal, with
![]() $p_1 , \dots , p_n$
smooth points of C. We say that
$p_1 , \dots , p_n$
smooth points of C. We say that
![]() $(C,p_1,\dots , p_n)$
is
$(C,p_1,\dots , p_n)$
is
![]() $\mathcal {A}$
-stable if
$\mathcal {A}$
-stable if
-
(i) the twisted canonical sheaf
 $K_C + a_1p_1 +\ldots +a_np_n$
is ample;
$K_C + a_1p_1 +\ldots +a_np_n$
is ample; -
(ii) whenever a subset of the marked points
 $p_i$
for
$p_i$
for
 $i\in S \subset \{1,\dots , n\}$
coincide, we have
$i\in S \subset \{1,\dots , n\}$
coincide, we have
 $\sum _{i\in S} a_i \leq 1.$
$\sum _{i\in S} a_i \leq 1.$
Equivalently, condition (i) is that for each irreducible component E of C, we have
see [Reference Ulirsch30, Proposition 3.3]. Hassett shows that there exists a connected Deligne-Mumford stack
![]() $\overline {\mathcal {M}}_{g,\mathcal {A}}$
of dimension
$\overline {\mathcal {M}}_{g,\mathcal {A}}$
of dimension
![]() $3g - 3 + n$
, smooth and proper over
$3g - 3 + n$
, smooth and proper over
![]() $\mathbb {Z}$
, which parameterizes
$\mathbb {Z}$
, which parameterizes
![]() $\mathcal {A}$
-stable curves of genus g [Reference Hassett15]. When
$\mathcal {A}$
-stable curves of genus g [Reference Hassett15]. When
![]() $\mathcal {A} =(1,\dots , 1)$
is a sequence of n ones, Hassett stability coincides with the Deligne–Mumford–Knudsen stability, and
$\mathcal {A} =(1,\dots , 1)$
is a sequence of n ones, Hassett stability coincides with the Deligne–Mumford–Knudsen stability, and
![]() $\overline {\mathcal {M}}_{g,\mathcal {A}} =\overline {\mathcal {M}}_{g,n}$
. Each stack
$\overline {\mathcal {M}}_{g,\mathcal {A}} =\overline {\mathcal {M}}_{g,n}$
. Each stack
![]() $\overline {\mathcal {M}}_{g, \mathcal {A}}$
is equipped with a birational morphism
$\overline {\mathcal {M}}_{g, \mathcal {A}}$
is equipped with a birational morphism
In this paper, we are interested in the family of weight data
 $$\begin{align*}\mathcal{A}_{m,n} = \left(\underbrace{1,\ldots, 1}_{m}, \underbrace{1/n, \ldots, 1/n}_{n} \right),\end{align*}$$
$$\begin{align*}\mathcal{A}_{m,n} = \left(\underbrace{1,\ldots, 1}_{m}, \underbrace{1/n, \ldots, 1/n}_{n} \right),\end{align*}$$
and as in the introduction, we put
![]() $\overline {\mathcal {M}}_{g, m|n}$
for the resulting moduli space, called the heavy/light Hassett space. We say that a curve is
$\overline {\mathcal {M}}_{g, m|n}$
for the resulting moduli space, called the heavy/light Hassett space. We say that a curve is
![]() $(m|n)$
-stable if it is
$(m|n)$
-stable if it is
![]() $\mathcal {A}_{m,n}$
-stable. We now characterize
$\mathcal {A}_{m,n}$
-stable. We now characterize
![]() $(m|n)$
-stability in combinatorial terms.
$(m|n)$
-stability in combinatorial terms.
Definition 2.6. For
![]() $(C, p_1, \ldots , p_{m + n}) \in \overline {\mathcal {M}}_{g, m + n}$
, let
$(C, p_1, \ldots , p_{m + n}) \in \overline {\mathcal {M}}_{g, m + n}$
, let
![]() $T \subset C$
be a union of irreducible components of C. We say T is a rational tail if T is a connected curve of arithmetic genus zero, and T meets
$T \subset C$
be a union of irreducible components of C. We say T is a rational tail if T is a connected curve of arithmetic genus zero, and T meets
![]() $\overline {C \smallsetminus T}$
in a single point.
$\overline {C \smallsetminus T}$
in a single point.
The following lemma is a straightforward application of (2.5), so we omit the proof.
Lemma 2.7. Let
![]() $(C, p_1, \ldots , p_ {m+n}) \in \overline {\mathcal {M}}_{g, m+n}$
. Then C is
$(C, p_1, \ldots , p_ {m+n}) \in \overline {\mathcal {M}}_{g, m+n}$
. Then C is
![]() $(m|n)$
-stable if and only if every rational tail of C contains at least one marking with index in
$(m|n)$
-stable if and only if every rational tail of C contains at least one marking with index in
![]() $\{1, \ldots , n\}$
.
$\{1, \ldots , n\}$
.
3. The Grothendieck ring of
 $\mathbb {S}^2$
-spaces
$\mathbb {S}^2$
-spaces
A G-variety is a variety with an action of a group G. An
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {X}$
is a sequence of
$\mathcal {X}$
is a sequence of
![]() $S_n$
-varieties
$S_n$
-varieties
![]() $\mathcal {X}(n)$
for
$\mathcal {X}(n)$
for
![]() $n \geq 0$
. Getzler–Pandharipande define a Grothendieck ring of
$n \geq 0$
. Getzler–Pandharipande define a Grothendieck ring of
![]() $\mathbb {S}$
-spaces [Reference Getzler and Pandharipande14]. We briefly generalize this formalism to the case of
$\mathbb {S}$
-spaces [Reference Getzler and Pandharipande14]. We briefly generalize this formalism to the case of
![]() $(S_m \times S_n)$
-varieties. First, we define the Grothendieck group
$(S_m \times S_n)$
-varieties. First, we define the Grothendieck group
of
![]() $(S_m \times S_n)$
-varieties. This group is constructed by first taking the free abelian group generated by isomorphism classes of
$(S_m \times S_n)$
-varieties. This group is constructed by first taking the free abelian group generated by isomorphism classes of
![]() $(S_m \times S_n)$
-varieties, and then imposing the relation
$(S_m \times S_n)$
-varieties, and then imposing the relation
whenever Y is an
![]() $(S_m \times S_n)$
-invariant subvariety of X. We define an
$(S_m \times S_n)$
-invariant subvariety of X. We define an
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\mathcal {X}$
to be a collection of varieties
$\mathcal {X}$
to be a collection of varieties
![]() $\mathcal {X}(m,n)$
together with an action of
$\mathcal {X}(m,n)$
together with an action of
![]() $S_m \times S_n$
for each pair
$S_m \times S_n$
for each pair
![]() $(m,n)$
with
$(m,n)$
with
![]() $m,n\geq 0$
. We refer to
$m,n\geq 0$
. We refer to
![]() $\mathcal {X}(m,n)$
as the arity
$\mathcal {X}(m,n)$
as the arity
![]() $(m,n)$
component of
$(m,n)$
component of
![]() $\mathcal {X}$
. We define the Grothendieck group of
$\mathcal {X}$
. We define the Grothendieck group of
![]() $\mathbb {S}^2$
-spaces as the product
$\mathbb {S}^2$
-spaces as the product
We can make
![]() $K_0(\mathsf {Var}, \mathbb {S}^2)$
into a ring using the
$K_0(\mathsf {Var}, \mathbb {S}^2)$
into a ring using the
![]() $\boxtimes $
-product on
$\boxtimes $
-product on
![]() $\mathbb {S}^2$
-spaces:
$\mathbb {S}^2$
-spaces:
 $$\begin{align*}(\mathcal{X} \boxtimes \mathcal{Y})(m,n) = \coprod_{i = 0}^{m} \coprod_{j = 0}^{n} \operatorname{Ind}_{S_i \times S_{m - i} \times S_{j} \times S_{n - j}}^{S_{m} \times S_n} \mathcal{X}(i, j) \times \mathcal{Y}(m-i,n-j). \end{align*}$$
$$\begin{align*}(\mathcal{X} \boxtimes \mathcal{Y})(m,n) = \coprod_{i = 0}^{m} \coprod_{j = 0}^{n} \operatorname{Ind}_{S_i \times S_{m - i} \times S_{j} \times S_{n - j}}^{S_{m} \times S_n} \mathcal{X}(i, j) \times \mathcal{Y}(m-i,n-j). \end{align*}$$
This generalizes the box product on
![]() $K_0(\mathsf {Var}, \mathbb {S})$
, given by
$K_0(\mathsf {Var}, \mathbb {S})$
, given by
 $$\begin{align*}(\mathcal{X} \boxtimes \mathcal{Y})(n) = \coprod_{j = 0}^{n} \operatorname{Ind}_{S_j \times S_n-j}^{S_n} \mathcal{X}(j) \times \mathcal{Y}(n-j). \end{align*}$$
$$\begin{align*}(\mathcal{X} \boxtimes \mathcal{Y})(n) = \coprod_{j = 0}^{n} \operatorname{Ind}_{S_j \times S_n-j}^{S_n} \mathcal{X}(j) \times \mathcal{Y}(n-j). \end{align*}$$
The ring
![]() $K_0(\mathsf {Var}, \mathbb {S}^2)$
is an algebra over the subring
$K_0(\mathsf {Var}, \mathbb {S}^2)$
is an algebra over the subring
![]() $K_0(\mathsf {Var}) = K_0(\mathsf {Var}, S_0 \times S_0)$
, which is nothing but the usual Grothendieck group of varieties. We will make use of a certain composition structure on the Grothendieck ring of
$K_0(\mathsf {Var}) = K_0(\mathsf {Var}, S_0 \times S_0)$
, which is nothing but the usual Grothendieck group of varieties. We will make use of a certain composition structure on the Grothendieck ring of
![]() $\mathbb {S}^2$
-spaces: we will compose an
$\mathbb {S}^2$
-spaces: we will compose an
![]() $\mathbb {S}^2$
-space with an
$\mathbb {S}^2$
-space with an
![]() $\mathbb {S}$
-space, as follows. Given
$\mathbb {S}$
-space, as follows. Given
![]() $\mathcal {X}$
a
$\mathcal {X}$
a
![]() $\mathbb {S}^2$
-space and
$\mathbb {S}^2$
-space and
![]() $\mathcal {Y}$
an
$\mathcal {Y}$
an
![]() $\mathbb {S}$
-space with
$\mathbb {S}$
-space with
![]() $\mathcal {Y}(0) = \varnothing $
, we can define two composition operations,
$\mathcal {Y}(0) = \varnothing $
, we can define two composition operations,
![]() $\circ _1$
and
$\circ _1$
and
![]() $\circ _2$
:
$\circ _2$
:
 $$ \begin{align} (\mathcal{X} \circ_1 \mathcal{Y})(m,n) = \coprod_{i = 0}^{\infty} (\mathcal{X}(i, n) \times \mathcal{Y}^{\boxtimes i}(m))/S_i, \end{align} $$
$$ \begin{align} (\mathcal{X} \circ_1 \mathcal{Y})(m,n) = \coprod_{i = 0}^{\infty} (\mathcal{X}(i, n) \times \mathcal{Y}^{\boxtimes i}(m))/S_i, \end{align} $$
and
 $$ \begin{align} (\mathcal{X} \circ_2 \mathcal{Y})(m,n) = \coprod_{j = 0}^{\infty}(\mathcal{X}(m, j) \times \mathcal{Y}^{\boxtimes j}(n))/S_j. \end{align} $$
$$ \begin{align} (\mathcal{X} \circ_2 \mathcal{Y})(m,n) = \coprod_{j = 0}^{\infty}(\mathcal{X}(m, j) \times \mathcal{Y}^{\boxtimes j}(n))/S_j. \end{align} $$
Given an
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\mathcal {X}$
, we define its Hodge–Deligne series by
$\mathcal {X}$
, we define its Hodge–Deligne series by
The lift of this series to the Grothendieck ring of mixed Hodge structures has been called the Serre characteristic or the Hodge-Grothendieck characteristic [Reference Bagnarol1].
The composition operations (3.1) and (3.2) should be viewed as categorifications of plethysm in the following sense: if
![]() $\mathcal {X}$
is an
$\mathcal {X}$
is an
![]() $\mathbb {S}^2$
-space, and
$\mathbb {S}^2$
-space, and
![]() $\mathcal {Y}$
is an
$\mathcal {Y}$
is an
![]() $\mathbb {S}$
-space, then
$\mathbb {S}$
-space, then
for
![]() $i = 1, 2$
, where for an
$i = 1, 2$
, where for an
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {Z}$
, one defines
$\mathcal {Z}$
, one defines
This follows upon upgrading Proposition 2.1 from
![]() $\mathbb {S}^2$
-modules in vector spaces to
$\mathbb {S}^2$
-modules in vector spaces to
![]() $\mathbb {S}^2$
-modules in the category of graded rational mixed Hodge structures, as is done for
$\mathbb {S}^2$
-modules in the category of graded rational mixed Hodge structures, as is done for
![]() $\mathbb {S}$
-modules in Getzler [Reference Getzler11] and Getzler–Pandharipande [Reference Getzler and Pandharipande14, §5]. We will put
$\mathbb {S}$
-modules in Getzler [Reference Getzler11] and Getzler–Pandharipande [Reference Getzler and Pandharipande14, §5]. We will put
![]() $\nu _n$
for the
$\nu _n$
for the
![]() $\mathbb {S}$
-space supported in arity n, where it is given by
$\mathbb {S}$
-space supported in arity n, where it is given by
![]() $\operatorname {Spec} \mathbb {C}$
with trivial action of
$\operatorname {Spec} \mathbb {C}$
with trivial action of
![]() $S_n$
. Note that
$S_n$
. Note that
Given an
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {X}$
with
$\mathcal {X}$
with
![]() $\mathcal {X}(0) = \varnothing $
, define an analogue of the exponential function
$\mathcal {X}(0) = \varnothing $
, define an analogue of the exponential function
![]() $e^x - 1$
by
$e^x - 1$
by
Finally, given an
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {Z}$
, we define an
$\mathcal {Z}$
, we define an
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\Delta \mathcal {Z}$
by the assignment
$\Delta \mathcal {Z}$
by the assignment
We have
by (2.2).
4. Proof of Theorem A
Our main theorem is proven using the composition operations defined above. First, for each
![]() $g \geq 0$
, define
$g \geq 0$
, define
![]() $\mathbb {S}^2$
-spaces as follows:
$\mathbb {S}^2$
-spaces as follows:
 $$ \begin{align} \mathcal{M}_g^{\mathrm{hl}}(m,n) = \begin{cases} \mathcal{M}_{g, m|n} &\text{ if } 2g - 2 + m + \text{min}(n, 1)> 0, \\ \varnothing &\text{ else}, \end{cases} \end{align} $$
$$ \begin{align} \mathcal{M}_g^{\mathrm{hl}}(m,n) = \begin{cases} \mathcal{M}_{g, m|n} &\text{ if } 2g - 2 + m + \text{min}(n, 1)> 0, \\ \varnothing &\text{ else}, \end{cases} \end{align} $$
 $$ \begin{align} \overline{\mathcal{M}}_g^{\mathrm{hl}}(m,n) = \begin{cases} \overline{\mathcal{M}}_{g, m|n} &\text{ if } 2g - 2 + m + \text{min}(n, 1)> 0, \\ \varnothing &\text{ else}. \end{cases} \end{align} $$
$$ \begin{align} \overline{\mathcal{M}}_g^{\mathrm{hl}}(m,n) = \begin{cases} \overline{\mathcal{M}}_{g, m|n} &\text{ if } 2g - 2 + m + \text{min}(n, 1)> 0, \\ \varnothing &\text{ else}. \end{cases} \end{align} $$
We will also make use of the
![]() $\mathbb {S}$
-spaces
$\mathbb {S}$
-spaces
 $$\begin{align*}\mathcal{M}_g(n) = \begin{cases} \mathcal{M}_{g,n} &\text{ if } 2g - 2 + n> 0, \\ \varnothing &\text{ else}, \end{cases} \end{align*}$$
$$\begin{align*}\mathcal{M}_g(n) = \begin{cases} \mathcal{M}_{g,n} &\text{ if } 2g - 2 + n> 0, \\ \varnothing &\text{ else}, \end{cases} \end{align*}$$
and
 $$\begin{align*}\overline{\mathcal{M}}_g(n) = \begin{cases} \overline{\mathcal{M}}_{g,n} &\text{ if } 2g - 2 + n> 0, \\ \varnothing &\text{ else}. \end{cases} \end{align*}$$
$$\begin{align*}\overline{\mathcal{M}}_g(n) = \begin{cases} \overline{\mathcal{M}}_{g,n} &\text{ if } 2g - 2 + n> 0, \\ \varnothing &\text{ else}. \end{cases} \end{align*}$$
Proposition 4.3. We have
Proof. Define the
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {Y}$
by
$\mathcal {Y}$
by
We have that
![]() $\mathcal {Y}(0) = \varnothing $
, while
$\mathcal {Y}(0) = \varnothing $
, while
![]() $\mathcal {Y}(n) = \nu _n$
for
$\mathcal {Y}(n) = \nu _n$
for
![]() $n \geq 1$
. For any
$n \geq 1$
. For any
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\mathcal {X}$
, we have
$\mathcal {X}$
, we have
 $$ \begin{align*} (\mathcal{X} \circ_2 \mathcal{Y})(m,n) &= \coprod_{j = 0}^{\infty} \left(\mathcal{X}(m, j) \times \mathcal{Y}^{\boxtimes j}(n) \right)/S_j \\&= \coprod_{j = 0}^{\infty} \left(\mathcal{X}(m, j) \times \coprod_{\substack{{k_1 + \cdots + k_j = n}\\{k_r> 0 \,\forall\, r}}} \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C} \right)/S_j. \end{align*} $$
$$ \begin{align*} (\mathcal{X} \circ_2 \mathcal{Y})(m,n) &= \coprod_{j = 0}^{\infty} \left(\mathcal{X}(m, j) \times \mathcal{Y}^{\boxtimes j}(n) \right)/S_j \\&= \coprod_{j = 0}^{\infty} \left(\mathcal{X}(m, j) \times \coprod_{\substack{{k_1 + \cdots + k_j = n}\\{k_r> 0 \,\forall\, r}}} \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C} \right)/S_j. \end{align*} $$
Now let us return to the
![]() $S_m \times S_n$
space
$S_m \times S_n$
space
![]() $\mathcal {M}_{g, m|n}$
. This space admits a stratification: for
$\mathcal {M}_{g, m|n}$
. This space admits a stratification: for
![]() $1 \leq j \leq n$
, let
$1 \leq j \leq n$
, let
![]() $\mathcal {Z}_{m,j} \subset \mathcal {M}_{g, m|n}$
denote the locally closed stratum in which there are precisely j distinct marked points among the last n. Then we can write
$\mathcal {Z}_{m,j} \subset \mathcal {M}_{g, m|n}$
denote the locally closed stratum in which there are precisely j distinct marked points among the last n. Then we can write
 $$ \begin{align} \mathcal{Z}_{m,j} \cong \left(\coprod_{\substack{{k_1 + \cdots + k_j = n}\\{k_r> 0 \, \forall \, r}}} \operatorname{Res}^{S_{m + j}}_{S_m \times S_j} \mathcal{M}_{g, m + j} \times \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C}\right)/S_j. \end{align} $$
$$ \begin{align} \mathcal{Z}_{m,j} \cong \left(\coprod_{\substack{{k_1 + \cdots + k_j = n}\\{k_r> 0 \, \forall \, r}}} \operatorname{Res}^{S_{m + j}}_{S_m \times S_j} \mathcal{M}_{g, m + j} \times \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C}\right)/S_j. \end{align} $$
Since
 $$\begin{align*}[\mathcal{M}_{g}^{\mathrm{hl}}(m, n)] = \sum_{j = 1}^{n} [\mathcal{Z}_{m,j}], \end{align*}$$
$$\begin{align*}[\mathcal{M}_{g}^{\mathrm{hl}}(m, n)] = \sum_{j = 1}^{n} [\mathcal{Z}_{m,j}], \end{align*}$$
we see that
upon summing over j, m and n on both sides of (4.4).
Towards proving our theorem for the compact moduli space
![]() $\overline {\mathcal {M}}_{g}^{\mathrm {hl}}$
, it is useful to introduce an auxiliary moduli space.
$\overline {\mathcal {M}}_{g}^{\mathrm {hl}}$
, it is useful to introduce an auxiliary moduli space.
Definition 4.5. We set
to be the locus of curves which have no rational tails whose support consists of any subset of the last k markings. We define an
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\overline {\mathcal {M}}^\star _g$
by
$\overline {\mathcal {M}}^\star _g$
by
The following proposition expresses the
![]() $\mathbb {S}^2$
-space
$\mathbb {S}^2$
-space
![]() $\Delta \overline {\mathcal {M}}_g$
in terms of
$\Delta \overline {\mathcal {M}}_g$
in terms of
![]() $\overline {\mathcal {M}}^{\star }_g$
and the composition operation. The basic idea has appeared in the literature before, in the main theorem of [Reference Getzler12]; see also [Reference Petersen25]. For an
$\overline {\mathcal {M}}^{\star }_g$
and the composition operation. The basic idea has appeared in the literature before, in the main theorem of [Reference Getzler12]; see also [Reference Petersen25]. For an
![]() $\mathbb {S}$
-space
$\mathbb {S}$
-space
![]() $\mathcal {Z}$
, we put
$\mathcal {Z}$
, we put
note that
by [Reference Getzler and Kapranov13, Proposition 8.10].
Proposition 4.6. Let
![]() $\overline {\mathcal {M}}_0^{\dagger }$
denote the
$\overline {\mathcal {M}}_0^{\dagger }$
denote the
![]() $\mathbb {S}$
-space that is empty in arities
$\mathbb {S}$
-space that is empty in arities
![]() $0$
and
$0$
and
![]() $1$
, supports
$1$
, supports
![]() $\operatorname {Spec} \mathbb {C}$
in arity
$\operatorname {Spec} \mathbb {C}$
in arity
![]() $2$
, and supports
$2$
, and supports
![]() $\overline {\mathcal {M}}_{0, n }$
in arities
$\overline {\mathcal {M}}_{0, n }$
in arities
![]() $n \geq 3$
. Then we have
$n \geq 3$
. Then we have
Proof. Let
![]() $\mathcal {X}$
denote the class on the right-hand side of the claimed equality, and note that
$\mathcal {X}$
denote the class on the right-hand side of the claimed equality, and note that
![]() $\mathcal {Y}= \delta \overline {\mathcal {M}}_0^{\dagger }$
is the
$\mathcal {Y}= \delta \overline {\mathcal {M}}_0^{\dagger }$
is the
![]() $\mathbb {S}$
-space which supports
$\mathbb {S}$
-space which supports
![]() $\varnothing $
in arity
$\varnothing $
in arity
![]() $0$
,
$0$
,
![]() $\nu _1$
in arity
$\nu _1$
in arity
![]() $1$
, and
$1$
, and
![]() $\mathrm {Res}^{S_{n + 1}}_{S_n} \mathcal {M}_{0, n + 1}$
in arities
$\mathrm {Res}^{S_{n + 1}}_{S_n} \mathcal {M}_{0, n + 1}$
in arities
![]() $n \geq 2$
. A point of the
$n \geq 2$
. A point of the
![]() $S_n$
-space
$S_n$
-space
![]() $\mathcal {Y}^{\boxtimes j}(n)$
corresponds to an ordered tuple of varieties
$\mathcal {Y}^{\boxtimes j}(n)$
corresponds to an ordered tuple of varieties
such that
-
1. for all i,
 $X_i$
is either
$X_i$
is either
 $\operatorname {Spec} \mathbb {C}$
or a pointed stable curve of arithmetic genus zero whose marked points are labelled by
$\operatorname {Spec} \mathbb {C}$
or a pointed stable curve of arithmetic genus zero whose marked points are labelled by
 $\{0, \ldots , r_i\}$
for some
$\{0, \ldots , r_i\}$
for some
 $r_i \geq 2$
;
$r_i \geq 2$
; -
2. there is a chosen bijection:
 $$\begin{align*}\{X_i \mid X_i = \operatorname{Spec} \mathbb{C} \} \cup \{p \mid p \text{ is a nonzero marked point of }X_j \text{ for some }j \} \to \{1, \dots, n\}.\end{align*}$$
$$\begin{align*}\{X_i \mid X_i = \operatorname{Spec} \mathbb{C} \} \cup \{p \mid p \text{ is a nonzero marked point of }X_j \text{ for some }j \} \to \{1, \dots, n\}.\end{align*}$$
The group
![]() $S_n$
acts on the chosen bijection, and
$S_n$
acts on the chosen bijection, and
![]() $S_j$
acts by reordering the tuple. Now recall that
$S_j$
acts by reordering the tuple. Now recall that
 $$ \begin{align*} \mathcal{X}(m,n) &= \coprod_{j = 0}^{\infty} \left(\overline{\mathcal{M}}^\star_g(m, j) \times \mathcal{Y}^{\boxtimes j}(n)\right)/S_j \\&= \coprod_{j = 0}^{n} \left(\overline{\mathcal{M}}^\star_g(m, j) \times \mathcal{Y}^{\boxtimes j}(n)\right)/S_j. \end{align*} $$
$$ \begin{align*} \mathcal{X}(m,n) &= \coprod_{j = 0}^{\infty} \left(\overline{\mathcal{M}}^\star_g(m, j) \times \mathcal{Y}^{\boxtimes j}(n)\right)/S_j \\&= \coprod_{j = 0}^{n} \left(\overline{\mathcal{M}}^\star_g(m, j) \times \mathcal{Y}^{\boxtimes j}(n)\right)/S_j. \end{align*} $$
We can see that the class
![]() $[\mathcal {X}(m, n)]$
in the Grothendieck group of
$[\mathcal {X}(m, n)]$
in the Grothendieck group of
![]() $(S_m \times S_n)$
-varieties is equal to
$(S_m \times S_n)$
-varieties is equal to
![]() $[\operatorname {Res}^{S_{m + n}}_{S_m \times S_n} \overline {\mathcal {M}}_{g, m+n}]$
. Indeed, for fixed j, one takes the ordered tuple
$[\operatorname {Res}^{S_{m + n}}_{S_m \times S_n} \overline {\mathcal {M}}_{g, m+n}]$
. Indeed, for fixed j, one takes the ordered tuple
![]() $(X_1, \ldots , X_j)$
represented by a point of
$(X_1, \ldots , X_j)$
represented by a point of
![]() $\mathcal {Y}^{\boxtimes j}(n)$
, and glues in the indicated order to the j distinguished marked points of a pointed curve in
$\mathcal {Y}^{\boxtimes j}(n)$
, and glues in the indicated order to the j distinguished marked points of a pointed curve in
![]() $\overline {\mathcal {M}}^\star _g(m, j)$
. This has the effect of adding rational tails which support subsets of the final n markings. Taking the quotient by the diagonal action of
$\overline {\mathcal {M}}^\star _g(m, j)$
. This has the effect of adding rational tails which support subsets of the final n markings. Taking the quotient by the diagonal action of
![]() $S_j$
makes this gluing procedure into an isomorphism between
$S_j$
makes this gluing procedure into an isomorphism between
![]() $\left (\overline {\mathcal {M}}^\star _g(m, j) \times \mathcal {Y}^{\boxtimes j}(n)\right )/S_j$
and the stratum of
$\left (\overline {\mathcal {M}}^\star _g(m, j) \times \mathcal {Y}^{\boxtimes j}(n)\right )/S_j$
and the stratum of
![]() $\operatorname {Res}^{S_{m + n}}_{S_m \times S_n} \overline {\mathcal {M}}_{g, m + n}$
where there are exactly j rational tails supporting subsets of the last n markings, where we allow for ‘trivial’ rational tails which are just marked points.
$\operatorname {Res}^{S_{m + n}}_{S_m \times S_n} \overline {\mathcal {M}}_{g, m + n}$
where there are exactly j rational tails supporting subsets of the last n markings, where we allow for ‘trivial’ rational tails which are just marked points.
The final ingredient of the proof of Theorem A is the following formula, analogous to Proposition 4.3.
Proposition 4.7. We have
Proof. The proof is essentially the same as that of Proposition 4.3: stratify
![]() $\overline {\mathcal {M}}_{g, m|n}$
by
$\overline {\mathcal {M}}_{g, m|n}$
by
and observe that
 $$\begin{align*}\mathcal{W}_{m ,j} \cong \coprod_{\substack{{k_1 + \cdots + k_j = n}\\k_r> 0\,\forall\,r }} \left(\overline{\mathcal{M}}_{g, m + j}^{(j)} \times \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C} \right)/S_j, \end{align*}$$
$$\begin{align*}\mathcal{W}_{m ,j} \cong \coprod_{\substack{{k_1 + \cdots + k_j = n}\\k_r> 0\,\forall\,r }} \left(\overline{\mathcal{M}}_{g, m + j}^{(j)} \times \operatorname{Ind}_{S_{k_1} \times \cdots \times S_{k_j}}^{S_n} \operatorname{Spec} \mathbb{C} \right)/S_j, \end{align*}$$
by Lemma 2.7. The proof is complete upon summing over m and j.
We can now prove the main theorem.
Proof of Theorem A.
The first part of the theorem follows from taking
![]() $\mathsf {e}(\cdot )$
on both sides of Proposition 4.3 and using both (3.3) and (3.4). From Proposition 4.6 and (3.4), we see that
$\mathsf {e}(\cdot )$
on both sides of Proposition 4.3 and using both (3.3) and (3.4). From Proposition 4.6 and (3.4), we see that
 $$ \begin{align} \Delta(\overline{\mathsf{a}}_g) = \mathsf{e}(\overline{\mathcal{M}}^{\star}_g) \circ_2 \left(p_1 + \frac{\partial \overline{\mathsf{b}}_0}{\partial p_1} \right)^{(2)}, \end{align} $$
$$ \begin{align} \Delta(\overline{\mathsf{a}}_g) = \mathsf{e}(\overline{\mathcal{M}}^{\star}_g) \circ_2 \left(p_1 + \frac{\partial \overline{\mathsf{b}}_0}{\partial p_1} \right)^{(2)}, \end{align} $$
as
![]() $\mathsf {e}(\nu _1) = p_1$
and
$\mathsf {e}(\nu _1) = p_1$
and
![]() $\mathsf {e}(\delta \overline {\mathcal {M}}_0) = \partial \overline {\mathsf {b}}_0/\partial p_1$
. The symmetric functions
$\mathsf {e}(\delta \overline {\mathcal {M}}_0) = \partial \overline {\mathsf {b}}_0/\partial p_1$
. The symmetric functions
 $$\begin{align*}p_1 + \frac{\partial \overline{\mathsf{b}}_0}{\partial p_1} \text{ and } p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1} \end{align*}$$
$$\begin{align*}p_1 + \frac{\partial \overline{\mathsf{b}}_0}{\partial p_1} \text{ and } p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1} \end{align*}$$
are plethystic inverses; this is because
![]() $\mathsf {b}_0$
and
$\mathsf {b}_0$
and
![]() $\overline {\mathsf {b}}_0$
are Legendre transforms of one another, as explained in [Reference Getzler10]. We thus perform the operation
$\overline {\mathsf {b}}_0$
are Legendre transforms of one another, as explained in [Reference Getzler10]. We thus perform the operation
 $$\begin{align*}\circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)} \end{align*}$$
$$\begin{align*}\circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)} \end{align*}$$
on both sides of (4.8) to see that
 $$ \begin{align*} \Delta(\overline{\mathsf{b}}_g) \circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)} = \mathsf{e}(\overline{\mathcal{M}}^{\star}_g). \end{align*} $$
$$ \begin{align*} \Delta(\overline{\mathsf{b}}_g) \circ_2 \left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)} = \mathsf{e}(\overline{\mathcal{M}}^{\star}_g). \end{align*} $$
The theorem is now proven upon applying Proposition 4.7.
To prove Corollary B, one uses the rank morphisms (2.3) and (2.4). We apply
![]() $\mathrm {rk}$
to both sides of Theorem A, and use that
$\mathrm {rk}$
to both sides of Theorem A, and use that
The corollary follows from the formula
 $$ \begin{align*} \mathrm{rk}\left(\left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)}\right) &= y - \sum_{n \geq 2} E_{\mathcal{M}_{0, n + 1}}(u, v) \cdot \frac{y^n}{n!} \\&= y + \frac{(y + 1)^{uv}- uvy - 1}{uv - u^2v^2}, \end{align*} $$
$$ \begin{align*} \mathrm{rk}\left(\left(p_1 - \frac{\partial \mathsf{b}_0}{\partial p_1}\right)^{(2)}\right) &= y - \sum_{n \geq 2} E_{\mathcal{M}_{0, n + 1}}(u, v) \cdot \frac{y^n}{n!} \\&= y + \frac{(y + 1)^{uv}- uvy - 1}{uv - u^2v^2}, \end{align*} $$
due to Getzler [Reference Getzler10].
5. Calculations
5.1. The Euler characteristic of
 $\overline {\mathcal {M}}_{1, 0|n}$
$\overline {\mathcal {M}}_{1, 0|n}$
We begin this section by proving two results on the topological Euler characteristic
![]() $\chi (\overline {\mathcal {M}}_{1, 0|n})$
, which may be viewed as corollaries of Theorem A and Getzler’s semi-classical approximation [Reference Getzler12]. The space
$\chi (\overline {\mathcal {M}}_{1, 0|n})$
, which may be viewed as corollaries of Theorem A and Getzler’s semi-classical approximation [Reference Getzler12]. The space
![]() $\overline {\mathcal {M}}_{1,0|n}$
is interesting to compare with
$\overline {\mathcal {M}}_{1,0|n}$
is interesting to compare with
![]() $\overline {\mathcal {M}}_{1, n}$
, as it parameterizes curves that have no rational tails. The first result determines the generating function for the numbers
$\overline {\mathcal {M}}_{1, n}$
, as it parameterizes curves that have no rational tails. The first result determines the generating function for the numbers
![]() $\chi (\overline {\mathcal {M}}_{1, 0|n})$
.
$\chi (\overline {\mathcal {M}}_{1, 0|n})$
.
Proposition 5.1. Define
 $$\begin{align*}f(y) : = \sum_{n \geq 1} \chi(\overline{\mathcal{M}}_{1, 0|n})\frac{y^n}{n!}. \end{align*}$$
$$\begin{align*}f(y) : = \sum_{n \geq 1} \chi(\overline{\mathcal{M}}_{1, 0|n})\frac{y^n}{n!}. \end{align*}$$
Then
where
Proof. Apply
![]() $\mathrm {rk}$
to both sides of Theorem A and consider the x-degree 0 part. We obtain an equality
$\mathrm {rk}$
to both sides of Theorem A and consider the x-degree 0 part. We obtain an equality
 $$ \begin{align*} \sum_n E_{\overline{\mathcal{M}}_{g,0|n}}(u,v) \frac{y^n}{n!} = \left(\sum_n E_{\overline{\mathcal{M}}_{g,n}}(u,v) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} E_{\mathcal{M}_{0,n+1}}(u,v) \frac{y^n}{n!}\right) \circ (e^y-1). \end{align*} $$
$$ \begin{align*} \sum_n E_{\overline{\mathcal{M}}_{g,0|n}}(u,v) \frac{y^n}{n!} = \left(\sum_n E_{\overline{\mathcal{M}}_{g,n}}(u,v) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} E_{\mathcal{M}_{0,n+1}}(u,v) \frac{y^n}{n!}\right) \circ (e^y-1). \end{align*} $$
We substitute
![]() $u=v=1$
and
$u=v=1$
and
![]() $g=1$
:
$g=1$
:
 $$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,0|n}) \frac{y^n}{n!} = \left(\sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ (e^y-1). \end{align*} $$
$$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,0|n}) \frac{y^n}{n!} = \left(\sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ (e^y-1). \end{align*} $$
Let
 $$\begin{align*}g(y) := y + \sum_{n \geq 2} \chi(\overline{\mathcal{M}}_{0, n+1}) \frac{y^n}{n!}, \end{align*}$$
$$\begin{align*}g(y) := y + \sum_{n \geq 2} \chi(\overline{\mathcal{M}}_{0, n+1}) \frac{y^n}{n!}, \end{align*}$$
so
 $$\begin{align*}g(y) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) = \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ g(y) = y,\end{align*}$$
$$\begin{align*}g(y) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) = \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ g(y) = y,\end{align*}$$
by [Reference Getzler10]. By [Reference Getzler12, Theorem 4.1], we have
 $$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}=-\frac{1}{12}\log(1+g(y)) - \frac12\log(1-\log(1+g(y))) + \varepsilon(g(y)), \end{align*} $$
$$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}=-\frac{1}{12}\log(1+g(y)) - \frac12\log(1-\log(1+g(y))) + \varepsilon(g(y)), \end{align*} $$
so we derive
 $$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,0|n}) \frac{y^n}{n!}&=\left(\sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ (e^y-1) \\ &=\left(-\frac{1}{12}\log(1+y) - \frac12\log(1-\log(1+y)) + \varepsilon(y)\right) \circ (e^y-1) \\ &=-\frac{y}{12} - \frac12\log(1-y) + \varepsilon \circ (e^y-1), \end{align*} $$
$$ \begin{align*} \sum_n \chi(\overline{\mathcal{M}}_{1,0|n}) \frac{y^n}{n!}&=\left(\sum_n \chi(\overline{\mathcal{M}}_{1,n}) \frac{y^n}{n!}\right) \circ \left(y-\sum_{n\geq 2} \chi(\mathcal{M}_{0,n+1}) \frac{y^n}{n!}\right) \circ (e^y-1) \\ &=\left(-\frac{1}{12}\log(1+y) - \frac12\log(1-\log(1+y)) + \varepsilon(y)\right) \circ (e^y-1) \\ &=-\frac{y}{12} - \frac12\log(1-y) + \varepsilon \circ (e^y-1), \end{align*} $$
as claimed.
The following corollary indicates that eliminating rational tails reduces the topological complexity of the moduli space.
Corollary 5.2. We have the asymptotic formulas
and
 $$\begin{align*}\frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} \sim 2(e - 2)^n. \end{align*}$$
$$\begin{align*}\frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} \sim 2(e - 2)^n. \end{align*}$$
In particular,
 $$\begin{align*}\lim_{n \to \infty} \frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} = 0. \end{align*}$$
$$\begin{align*}\lim_{n \to \infty} \frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} = 0. \end{align*}$$
Proof. If we think of y as a complex variable, the function
![]() $f(y)-(- \log (1 - y)/2)$
is an entire function. By [Reference Wilf31, Theorem 2.4.3], the values
$f(y)-(- \log (1 - y)/2)$
is an entire function. By [Reference Wilf31, Theorem 2.4.3], the values
![]() $\chi (\overline {\mathcal {M}}_{1,0|n})/n!$
are approximated by the power series coefficients of the function
$\chi (\overline {\mathcal {M}}_{1,0|n})/n!$
are approximated by the power series coefficients of the function
![]() $- \frac 12\log (1-y)$
about the origin. Therefore, we have
$- \frac 12\log (1-y)$
about the origin. Therefore, we have
By [Reference Getzler12, Corollary 4.2],
where C is a constant. Therefore,
 $$ \begin{align*} \frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} \sim \frac{(n-1)!}{2}\frac{4(e-2)^n}{(n-1)!}= 2(e- 2)^n, \end{align*} $$
$$ \begin{align*} \frac{\chi(\overline{\mathcal{M}}_{1,0|n})}{\chi(\overline{\mathcal{M}}_{1,n})} \sim \frac{(n-1)!}{2}\frac{4(e-2)^n}{(n-1)!}= 2(e- 2)^n, \end{align*} $$
as we wanted to show.
Corollary 5.2 implies that when n is large, the ‘all light points’ moduli space
![]() $\overline {\mathcal {M}}_{1, 0|n}$
has much less cohomology than the Deligne–Mumford moduli space
$\overline {\mathcal {M}}_{1, 0|n}$
has much less cohomology than the Deligne–Mumford moduli space
![]() $\overline {\mathcal {M}}_{1, n}$
. It is natural to ask whether the same holds for higher genus.
$\overline {\mathcal {M}}_{1, n}$
. It is natural to ask whether the same holds for higher genus.
Question 5.3. Find an asymptotic formula for the quotient
 $$\begin{align*}\frac{\chi(\overline{\mathcal{M}}_{g, 0|n})}{\chi(\overline{\mathcal{M}}_{g, n})} \end{align*}$$
$$\begin{align*}\frac{\chi(\overline{\mathcal{M}}_{g, 0|n})}{\chi(\overline{\mathcal{M}}_{g, n})} \end{align*}$$
for all
![]() $g \geq 2$
. Do we have
$g \geq 2$
. Do we have
 $$\begin{align*}\lim_{n \to \infty} \frac{\chi(\overline{\mathcal{M}}_{g, 0|n})}{\chi(\overline{\mathcal{M}}_{g, n})} = 0 \end{align*}$$
$$\begin{align*}\lim_{n \to \infty} \frac{\chi(\overline{\mathcal{M}}_{g, 0|n})}{\chi(\overline{\mathcal{M}}_{g, n})} = 0 \end{align*}$$
for all such g?
5.2. Tables of data
We conclude the paper by giving more context for the three tables in Section 1. The first, Table 1, contains the
![]() $(S_m \times S_n)$
-equivariant Hodge polynomial of
$(S_m \times S_n)$
-equivariant Hodge polynomial of
![]() $\overline {\mathcal {M}}_{1, m|n}$
for
$\overline {\mathcal {M}}_{1, m|n}$
for
![]() $m + n \leq 5$
. These rely on the calculation of the series
$m + n \leq 5$
. These rely on the calculation of the series
![]() $\overline {\mathsf {b}}_1$
by Getzler [Reference Getzler12]. For
$\overline {\mathsf {b}}_1$
by Getzler [Reference Getzler12]. For
![]() $n \leq 10$
, the mixed Hodge structures on the cohomology groups of the moduli space
$n \leq 10$
, the mixed Hodge structures on the cohomology groups of the moduli space
![]() $\overline {\mathcal {M}}_{1, n}$
are polynomials in
$\overline {\mathcal {M}}_{1, n}$
are polynomials in
![]() $\mathsf {L} = H^{2}_c(\mathbb {A}^1;\mathbb {C})$
, the mixed Hodge structure of the affine line. A consequence is that
$\mathsf {L} = H^{2}_c(\mathbb {A}^1;\mathbb {C})$
, the mixed Hodge structure of the affine line. A consequence is that
![]() $\overline {\mathcal {M}}_{1, n}$
has only even dimensional cohomology for
$\overline {\mathcal {M}}_{1, n}$
has only even dimensional cohomology for
![]() $n \leq 10$
, and only the diagonal Hodge numbers
$n \leq 10$
, and only the diagonal Hodge numbers
![]() $\dim H^{p,p}$
are nonzero. By Theorem A, the same is true for
$\dim H^{p,p}$
are nonzero. By Theorem A, the same is true for
![]() $\overline {\mathcal {M}}_{1, m|n}$
for
$\overline {\mathcal {M}}_{1, m|n}$
for
![]() $m + n \leq 10$
. Therefore, Table 1 displays the equivariant Poincaré polynomial
$m + n \leq 10$
. Therefore, Table 1 displays the equivariant Poincaré polynomial
and the Hodge polynomial can be recovered by setting
![]() $t^2 = uv$
.
$t^2 = uv$
.
Table 2 contains the non-equivariant Hodge polynomial of
![]() $\overline {\mathcal {M}}_{1, 0|n}$
for
$\overline {\mathcal {M}}_{1, 0|n}$
for
![]() $n \leq 11$
, computed with Corollary B and Getzler’s calculation of
$n \leq 11$
, computed with Corollary B and Getzler’s calculation of
![]() $\overline {b}_1$
. By Corollary 5.2, one might expect
$\overline {b}_1$
. By Corollary 5.2, one might expect
![]() $\overline {\mathcal {M}}_{1,0|n}$
to have less cohomology than
$\overline {\mathcal {M}}_{1,0|n}$
to have less cohomology than
![]() $\overline {\mathcal {M}}_{1, n}$
(this is not a direct consequence; both spaces may have odd cohomology). Indeed, comparing with the table [Reference Getzler12, p.491], we observe that
$\overline {\mathcal {M}}_{1, n}$
(this is not a direct consequence; both spaces may have odd cohomology). Indeed, comparing with the table [Reference Getzler12, p.491], we observe that
![]() $\dim H^*(\overline {\mathcal {M}}_{1, 0|10}) = 232,076$
while
$\dim H^*(\overline {\mathcal {M}}_{1, 0|10}) = 232,076$
while
![]() $\dim H^*(\overline {\mathcal {M}}_{1, 10}) = 16,275,872$
. One also notes that just as in the case of
$\dim H^*(\overline {\mathcal {M}}_{1, 10}) = 16,275,872$
. One also notes that just as in the case of
![]() $\overline {\mathcal {M}}_{1, 11}$
, the space
$\overline {\mathcal {M}}_{1, 11}$
, the space
![]() $\overline {\mathcal {M}}_{1, 0|11}$
has odd-dimensional cohomology; this is true of
$\overline {\mathcal {M}}_{1, 0|11}$
has odd-dimensional cohomology; this is true of
![]() $\overline {\mathcal {M}}_{1, m|n}$
whenever
$\overline {\mathcal {M}}_{1, m|n}$
whenever
![]() $m + n = 11$
.
$m + n = 11$
.
Finally, Table 3 contains the
![]() $(S_m \times S_n)$
-equivariant compactly supported weight zero Euler characteristic of
$(S_m \times S_n)$
-equivariant compactly supported weight zero Euler characteristic of
![]() $\mathcal {M}_{2, m|n}$
for
$\mathcal {M}_{2, m|n}$
for
![]() $m + n \leq 6$
, which is equal to
$m + n \leq 6$
, which is equal to
the constant term of the Hodge–Deligne polynomial. We also include the numerical weight zero Euler characteristic. This table was computed using the first part of Theorem A, together with the formula of Chan et al. for
![]() $E_{\mathcal {M}_{g, n}}^{S_n}(0,0)$
[Reference Chan, Faber, Galatius and Payne5]. We also note that this table and our techniques apply to compute the equivariant Euler characteristic
$E_{\mathcal {M}_{g, n}}^{S_n}(0,0)$
[Reference Chan, Faber, Galatius and Payne5]. We also note that this table and our techniques apply to compute the equivariant Euler characteristic
where
![]() $\Delta _{g, m|n}$
is the tropical heavy/light Hassett space, studied in [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Cerbu, Marcus, Peilen, Ranganathan and Salmon9, Reference Kannan, Li, Serpente and Yun19, Reference Kannan, Karp and Li18]. Indeed, one has
$\Delta _{g, m|n}$
is the tropical heavy/light Hassett space, studied in [Reference Cavalieri, Hampe, Markwig and Ranganathan7, Reference Cerbu, Marcus, Peilen, Ranganathan and Salmon9, Reference Kannan, Li, Serpente and Yun19, Reference Kannan, Karp and Li18]. Indeed, one has
when
![]() $\Delta _{g, m|n}$
is connected, which holds when
$\Delta _{g, m|n}$
is connected, which holds when
![]() $g \geq 1$
, and when
$g \geq 1$
, and when
![]() $g = 0$
and
$g = 0$
and
![]() $m + n> 4$
. See [Reference Kannan, Li, Serpente and Yun19, §4]. It is natural to ask whether there is a way to calculate
$m + n> 4$
. See [Reference Kannan, Li, Serpente and Yun19, §4]. It is natural to ask whether there is a way to calculate
![]() $E^{S_m \times S_n}_{\mathcal {M}_{g, m|n}}(0,0)$
which does not rely on the formula of [Reference Chan, Faber, Galatius and Payne5], together with plethysm.
$E^{S_m \times S_n}_{\mathcal {M}_{g, m|n}}(0,0)$
which does not rely on the formula of [Reference Chan, Faber, Galatius and Payne5], together with plethysm.
Question 5.4. Can the graph-theoretic methods of [Reference Chan, Faber, Galatius and Payne5] be adapted to give a closed formula for the weight zero compactly supported Euler characteristic
![]() $E^{S_m \times S_n}_{\mathcal {M}_{g, m|n}}(0,0)$
?
$E^{S_m \times S_n}_{\mathcal {M}_{g, m|n}}(0,0)$
?
We exclude the case
![]() $n = 1$
from Tables 1 and 3, as
$n = 1$
from Tables 1 and 3, as
 $$\begin{align*}E^{S_{m} \times S_1}_{\overline{\mathcal{M}}_{g, m|1}}(u,v) = \left( \frac{\partial E^{S_{m + 1}}_{\overline{\mathcal{M}}_{g, m + 1}}(u,v) }{\partial p_1} \right)^{(1)} \cdot s_{1}^{(2)}, \end{align*}$$
$$\begin{align*}E^{S_{m} \times S_1}_{\overline{\mathcal{M}}_{g, m|1}}(u,v) = \left( \frac{\partial E^{S_{m + 1}}_{\overline{\mathcal{M}}_{g, m + 1}}(u,v) }{\partial p_1} \right)^{(1)} \cdot s_{1}^{(2)}, \end{align*}$$
and the analogous formula holds for the open moduli spaces.
Acknowledgements
We thank Madeline Brandt, Melody Chan and Dhruv Ranganathan for useful conversations.
Competing interest
The authors do not have any competing interests.
Funding statement
SK was supported by an NSF Graduate Research Fellowship.