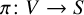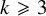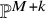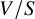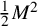Introduction
0.1 Fano complete intersections
In the present paper, we study the birational geometry of algebraic varieties, fibred into Fano complete intersections of codimension
![]() $k\geqslant 3$
(fibrations into Fano hypersurfaces were studied in [Reference Pukhlikov1], into Fano complete intersections of codimension 2 in [Reference Pukhlikov2]). We start with a description of fibres of these fibre spaces. Let us fix an integer
$k\geqslant 3$
(fibrations into Fano hypersurfaces were studied in [Reference Pukhlikov1], into Fano complete intersections of codimension 2 in [Reference Pukhlikov2]). We start with a description of fibres of these fibre spaces. Let us fix an integer
![]() $k\geqslant 3$
and set
$k\geqslant 3$
and set
 $$ \begin{align*}\varepsilon(k)=\mathop{\mathrm{min}} \left\{a\in {\mathbb Z}\,\left|\, a\geqslant 1, \left(1+\frac{1}{k}\right.\right)^a\geqslant 2\right\}. \end{align*} $$
$$ \begin{align*}\varepsilon(k)=\mathop{\mathrm{min}} \left\{a\in {\mathbb Z}\,\left|\, a\geqslant 1, \left(1+\frac{1}{k}\right.\right)^a\geqslant 2\right\}. \end{align*} $$
Now let us fix
![]() $M\in {\mathbb Z}$
, satisfying the inequality
$M\in {\mathbb Z}$
, satisfying the inequality
The right-hand side of that inequality denote by the symbol
![]() $\rho (k)$
. Let
$\rho (k)$
. Let
be an ordered tuple of integers,
satisfying the equality
Fano varieties, considered in this paper, are complete intersections of type
![]() $\underline {d}$
in the complex projective space
$\underline {d}$
in the complex projective space
![]() ${\mathbb P}^{M+k}$
. More precisely, let the symbol
${\mathbb P}^{M+k}$
. More precisely, let the symbol
![]() ${\cal P}_{a,N}$
stand for the space of homogeneous polynomials of degree
${\cal P}_{a,N}$
stand for the space of homogeneous polynomials of degree
![]() $a\in {\mathbb Z}_+$
in
$a\in {\mathbb Z}_+$
in
![]() $N\geqslant 1$
variables. Set
$N\geqslant 1$
variables. Set
 $$ \begin{align*}{\cal P}=\prod^k_{i=1} {\cal P}_{d_i,M+k+1} \end{align*} $$
$$ \begin{align*}{\cal P}=\prod^k_{i=1} {\cal P}_{d_i,M+k+1} \end{align*} $$
to be the space of all tuples
of homogeneous polynomials of degree
![]() $d_1$
, …,
$d_1$
, …,
![]() $d_k$
on
$d_k$
on
![]() ${\mathbb P}^{M+k}$
. If for
${\mathbb P}^{M+k}$
. If for
![]() $\underline {f}\in {\cal P}$
the scheme of common zeros of the polynomials
$\underline {f}\in {\cal P}$
the scheme of common zeros of the polynomials
![]() $f_1,\dots , f_k$
is an irreducible reduced factorial variety
$f_1,\dots , f_k$
is an irreducible reduced factorial variety
![]() $F=F(\underline {f})$
of dimension M with terminal singularities, then F is a primitive Fano variety:
$F=F(\underline {f})$
of dimension M with terminal singularities, then F is a primitive Fano variety:
where
![]() $H_F$
is the class of a hyperplane section of the variety F (the Lefschetz theorem). Assuming that this is the case, let us give the following definition.
$H_F$
is the class of a hyperplane section of the variety F (the Lefschetz theorem). Assuming that this is the case, let us give the following definition.
Definition 0.1. The variety F is divisorially canonical, if for every effective divisor
![]() $D\sim nH_F$
, the pair
$D\sim nH_F$
, the pair
![]() $(F,\frac {1}{n}D)$
is canonical – that is, for every exceptional divisor E over F, the inequality
$(F,\frac {1}{n}D)$
is canonical – that is, for every exceptional divisor E over F, the inequality
holds, where
![]() $a(E)$
is the discrepancy of E with respect to F.
$a(E)$
is the discrepancy of E with respect to F.
Below is the first main result of the present paper.
Theorem 0.1. There exist a Zariski open subset
![]() ${\cal F}\subset {\cal P}$
, such that for every tuple
${\cal F}\subset {\cal P}$
, such that for every tuple
![]() $\underline {f}\in {\cal F}$
, the scheme of common zeros of the tuple
$\underline {f}\in {\cal F}$
, the scheme of common zeros of the tuple
![]() $\underline {f}$
is an irreducible reduced factorial divisorially canonical variety
$\underline {f}$
is an irreducible reduced factorial divisorially canonical variety
![]() $F(\underline {f})$
of dimension M with terminal singularities, and the codimension of the complement
$F(\underline {f})$
of dimension M with terminal singularities, and the codimension of the complement
![]() ${\cal P}\setminus {\cal F}$
satisfies the inequality
${\cal P}\setminus {\cal F}$
satisfies the inequality
 $$ \begin{align*}\mathop{\mathrm{codim}}(({\cal P}\setminus{\cal F})\subset{\cal P}) \geqslant M-k+5+{M-\rho(k)+2 \choose 2}. \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{codim}}(({\cal P}\setminus{\cal F})\subset{\cal P}) \geqslant M-k+5+{M-\rho(k)+2 \choose 2}. \end{align*} $$
(Thus, for a fixed k and growing M, the codimension of the complement
![]() ${\cal P}\setminus {\cal F}$
grows as
${\cal P}\setminus {\cal F}$
grows as
![]() $\frac 12 M^2$
.)
$\frac 12 M^2$
.)
It is convenient to express the property of divisorial canonicity in terms of the global canonical threshold of the variety F.
Recall that for a Fano variety X with the Picard number 1 and terminal
![]() ${\mathbb Q}$
-factorial singularities, its global canonical threshold
${\mathbb Q}$
-factorial singularities, its global canonical threshold
![]() $\mathop {\mathrm {ct}}(X)$
is the supremum of
$\mathop {\mathrm {ct}}(X)$
is the supremum of
![]() $\lambda \in {\mathbb Q}_+$
such that for every effective divisor
$\lambda \in {\mathbb Q}_+$
such that for every effective divisor
![]() $D\sim -nK_X$
(here,
$D\sim -nK_X$
(here,
![]() $n\in {\mathbb Q}_+$
), the pair
$n\in {\mathbb Q}_+$
), the pair
![]() $\left(X,\frac {\lambda }{n}D\right)$
is canonical. Therefore, Theorem 0.1 claims that for every
$\left(X,\frac {\lambda }{n}D\right)$
is canonical. Therefore, Theorem 0.1 claims that for every
![]() $\underline {f}\in {\cal F}$
, the inequality
$\underline {f}\in {\cal F}$
, the inequality
![]() $\mathop {\mathrm {ct}} (F(\underline {f}))\geqslant 1$
holds.
$\mathop {\mathrm {ct}} (F(\underline {f}))\geqslant 1$
holds.
If in the definition of the global canonical threshold instead of ‘for every effective divisor
![]() $D\sim -nK_X$
’, we put ‘for a general divisor D in any linear system
$D\sim -nK_X$
’, we put ‘for a general divisor D in any linear system
![]() $\Sigma \subset |-nK_X|$
with no fixed components’, we get the definition of the mobile canonical threshold
$\Sigma \subset |-nK_X|$
with no fixed components’, we get the definition of the mobile canonical threshold
![]() $\mathop {\mathrm {mct}}(X)$
; obviously,
$\mathop {\mathrm {mct}}(X)$
; obviously,
![]() $\mathop {\mathrm {mct}}(X)\geqslant \mathop {\mathrm {ct}}(X)$
. The inequality
$\mathop {\mathrm {mct}}(X)\geqslant \mathop {\mathrm {ct}}(X)$
. The inequality
![]() $\mathop {\mathrm {mct}}(X)\geqslant 1$
is equivalent to the birational superrigidity of the Fano variety X; see [Reference Cheltsov3]. If in the definition of the global canonical threshold the property of the pair
$\mathop {\mathrm {mct}}(X)\geqslant 1$
is equivalent to the birational superrigidity of the Fano variety X; see [Reference Cheltsov3]. If in the definition of the global canonical threshold the property of the pair
![]() $(X,\frac {\lambda }{n}D)$
to be canonical, we replace by the log-canonicity of that pair, we get the definition of the global log-canonical threshold
$(X,\frac {\lambda }{n}D)$
to be canonical, we replace by the log-canonicity of that pair, we get the definition of the global log-canonical threshold
![]() $\mathop {\mathrm {lct}}(X)$
; again,
$\mathop {\mathrm {lct}}(X)$
; again,
![]() $\mathop {\mathrm {lct}}(X)\geqslant \mathop {\mathrm {ct}}(X)$
.
$\mathop {\mathrm {lct}}(X)\geqslant \mathop {\mathrm {ct}}(X)$
.
For simplicity, we write
![]() $F\in {\cal F}$
instead of
$F\in {\cal F}$
instead of
![]() $F=F(\underline {f})$
for
$F=F(\underline {f})$
for
![]() $\underline {f}\in {\cal F}$
.
$\underline {f}\in {\cal F}$
.
0.2 Fano-Mori fibre spaces
By a Fano-Mori fibre space we mean a surjective morphism of projective varieties
where
![]() $\dim V\geqslant 3 + \dim S$
, the base S is non-singular and rationally connected, and the following conditions are satisfied:
$\dim V\geqslant 3 + \dim S$
, the base S is non-singular and rationally connected, and the following conditions are satisfied:
(FM1) every scheme fibre
![]() $F_s=\pi ^{-1}(s)$
,
$F_s=\pi ^{-1}(s)$
,
![]() $s\in S$
is an irreducible reduced factorial Fano variety with terminal singularities and the Picard group
$s\in S$
is an irreducible reduced factorial Fano variety with terminal singularities and the Picard group
![]() $\mathop {\mathrm {Pic}} F_s\cong {\mathbb Z}$
,
$\mathop {\mathrm {Pic}} F_s\cong {\mathbb Z}$
,
(FM2) the variety V itself is factorial and has at most terminal singularities,
(FM3) the equality
holds.
So Fano-Mori fibre spaces are Mori fibre spaces with additional very good properties.
Definition 0.2. A Fano-Mori fibre space
![]() $\pi \colon V\to S$
is stable with respect to fibre-wise birational modifications, if for every birational morphism
$\pi \colon V\to S$
is stable with respect to fibre-wise birational modifications, if for every birational morphism
![]() $\sigma _S\colon S^+\to S$
, where
$\sigma _S\colon S^+\to S$
, where
![]() $S^+$
is a non-singular projective variety, the morphism
$S^+$
is a non-singular projective variety, the morphism
is a Fano-Mori fibre space.
We will consider birational maps
![]() $\chi \colon V\dashrightarrow V'$
, where V is the total space of a Fano-Mori fibre space and
$\chi \colon V\dashrightarrow V'$
, where V is the total space of a Fano-Mori fibre space and
![]() $V'$
is the total space of a fibre space
$V'$
is the total space of a fibre space
![]() $\pi '\colon V'\to S'$
which belongs to one of the two classes:
$\pi '\colon V'\to S'$
which belongs to one of the two classes:
(1) rationally connected fibre spaces; that is,
![]() $V'$
and
$V'$
and
![]() $S'$
are non-singular and projective and the base
$S'$
are non-singular and projective and the base
![]() $S'$
and a fibre of general position
$S'$
and a fibre of general position
![]() $(\pi ')^{-1}(s')$
are rationally connected,
$(\pi ')^{-1}(s')$
are rationally connected,
(2) Mori fibre spaces, where
![]() $V'$
and
$V'$
and
![]() $S'$
are projective and the variety
$S'$
are projective and the variety
![]() $V'$
has
$V'$
has
![]() ${\mathbb Q}$
-factorial terminal singularities.
${\mathbb Q}$
-factorial terminal singularities.
For a birational map
![]() $\chi \colon V\dashrightarrow V'$
, where
$\chi \colon V\dashrightarrow V'$
, where
![]() $V'/S'$
is a rationally connected fibre space, we want to answer the question: is it fibre-wise – that is, is there a rational dominant map
$V'/S'$
is a rationally connected fibre space, we want to answer the question: is it fibre-wise – that is, is there a rational dominant map
![]() $\beta \colon S\dashrightarrow S'$
, making the diagram
$\beta \colon S\dashrightarrow S'$
, making the diagram
 $$ \begin{align} \begin{array}{rcccl} & V & \stackrel{\chi}{\dashrightarrow} & V' & \\ \pi\!\!\! & \downarrow & & \downarrow & \!\!\!\pi' \\ & S & \stackrel{\beta}{\dashrightarrow} & S' \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcccl} & V & \stackrel{\chi}{\dashrightarrow} & V' & \\ \pi\!\!\! & \downarrow & & \downarrow & \!\!\!\pi' \\ & S & \stackrel{\beta}{\dashrightarrow} & S' \end{array} \end{align} $$
a commutative one – that is,
![]() $\pi '\circ \chi =\beta \circ \pi $
?
$\pi '\circ \chi =\beta \circ \pi $
?
For a birational map
![]() $\chi \colon V\dashrightarrow V'$
, where
$\chi \colon V\dashrightarrow V'$
, where
![]() $V'/S'$
is a Mori fibre space with the additional properties (2) (only such Mori fibre spaces are considered in this paper), we want to answer the question: is there a birational map
$V'/S'$
is a Mori fibre space with the additional properties (2) (only such Mori fibre spaces are considered in this paper), we want to answer the question: is there a birational map
![]() $\beta \colon S\dashrightarrow S'$
, for which the diagram (2) is commutative? If the answer to this question is always affirmative (that is, it is affirmative for every fibre space from the class (2)), then the fibre space
$\beta \colon S\dashrightarrow S'$
, for which the diagram (2) is commutative? If the answer to this question is always affirmative (that is, it is affirmative for every fibre space from the class (2)), then the fibre space
![]() $V/S$
is birationally rigid.
$V/S$
is birationally rigid.
Now let us state the second main result of the present paper.
Theorem 0.2. Assume that a Fano-Mori fibre space
![]() $\pi \colon V\to S$
is stable with respect to fibre-wise birational modifications, and moreover,
$\pi \colon V\to S$
is stable with respect to fibre-wise birational modifications, and moreover,
(i) for every point
![]() $s\in S$
, the fibre
$s\in S$
, the fibre
![]() $F_s$
satisfies the inequalities
$F_s$
satisfies the inequalities
![]() $\mathop {\mathrm {lct}} (F_s)\geqslant 1$
and
$\mathop {\mathrm {lct}} (F_s)\geqslant 1$
and
![]() $\mathop {\mathrm {mct}} (F_s)\geqslant 1$
,
$\mathop {\mathrm {mct}} (F_s)\geqslant 1$
,
(ii) (the K-condition) every mobile (that is, with no fixed components) linear system on V is a subsystem of a complete linear system
![]() $|-nK_V+\pi ^* Y|$
, where Y is a pseudoeffective class on S,
$|-nK_V+\pi ^* Y|$
, where Y is a pseudoeffective class on S,
(iii) for every family
![]() ${\overline {\cal C}}$
of irreducible curves on S, sweeping out a dense subset of the base S, and
${\overline {\cal C}}$
of irreducible curves on S, sweeping out a dense subset of the base S, and
![]() $\overline {C}\in {\overline {\cal C}}$
, no positive multiple of the class
$\overline {C}\in {\overline {\cal C}}$
, no positive multiple of the class
where
![]() $A^iV$
is the numerical Chow group of classes of cycles of codimension i on V and F – the class of a fibre of the projection
$A^iV$
is the numerical Chow group of classes of cycles of codimension i on V and F – the class of a fibre of the projection
![]() $\pi $
– is represented by an effective cycle on V.
$\pi $
– is represented by an effective cycle on V.
Then for every rationally connected fibre space
![]() $V'/ S'$
, every birational map
$V'/ S'$
, every birational map
![]() $\chi \colon V\dashrightarrow V'$
(if such maps exist) is fibre-wise, and the fibre space
$\chi \colon V\dashrightarrow V'$
(if such maps exist) is fibre-wise, and the fibre space
![]() $V/ S$
itself is birationally rigid.
$V/ S$
itself is birationally rigid.
By what was said in Subsection 0.1, the assumption (i) can be replaced by the single inequality
![]() $\mathop {\mathrm {ct}}(F_s)\geqslant 1$
for every
$\mathop {\mathrm {ct}}(F_s)\geqslant 1$
for every
![]() $s\in S$
; that is, it is sufficient to assume that every fibre of the fibre space
$s\in S$
; that is, it is sufficient to assume that every fibre of the fibre space
![]() $V/ S$
is a divisorially canonical variety.
$V/ S$
is a divisorially canonical variety.
As we will see from the proof of Theorem 0.2, instead of the conditions (ii) and (iii), it is sufficient to require that for every family
![]() $\overline {\cal C}$
of irreducible curves on S, sweeping out a dense subset, and
$\overline {\cal C}$
of irreducible curves on S, sweeping out a dense subset, and
![]() $\overline {C}\in \overline {\cal C}$
the class
$\overline {C}\in \overline {\cal C}$
the class
is not represented by an effective cycle on V for any
![]() $N\geqslant 1$
. The last condition is especially easy to verify: it is enough to have a numerically effective
$N\geqslant 1$
. The last condition is especially easy to verify: it is enough to have a numerically effective
![]() $\pi $
-ample class
$\pi $
-ample class
![]() $H_V$
on V, satisfying the inequality
$H_V$
on V, satisfying the inequality
for every dense family
![]() $\overline {\cal C}\ni \overline {C}$
.
$\overline {\cal C}\ni \overline {C}$
.
0.3 An explicit construction of a fibre space
Now let us construct a large class of Fano-Mori fibre spaces, satisfying the conditions of Theorem 0.2. Let S be a non-singular projective rationally connected positive-dimensional variety and
![]() $\pi _X\colon X\to S$
a locally trivial fibration with the fibre
$\pi _X\colon X\to S$
a locally trivial fibration with the fibre
![]() ${\mathbb P}^{M+k}$
, where k and M are the same as in Subsection 0.1. We say that the subvariety
${\mathbb P}^{M+k}$
, where k and M are the same as in Subsection 0.1. We say that the subvariety
![]() $V\subset X$
of codimension k is a fibration into complete intersections of type
$V\subset X$
of codimension k is a fibration into complete intersections of type
![]() $\underline {d}$
, if the base S can be covered by Zariski open subsets U, over which the fibration
$\underline {d}$
, if the base S can be covered by Zariski open subsets U, over which the fibration
![]() $\pi _X$
is trivial,
$\pi _X$
is trivial,
![]() $\pi ^{-1}_X(U)\cong U\times {\mathbb P}^{M+k}$
, and for every U, there is a regular map
$\pi ^{-1}_X(U)\cong U\times {\mathbb P}^{M+k}$
, and for every U, there is a regular map
such that
![]() $V\cap \,\pi ^{-1}_X(U)$
in the sense of the above-mentioned trivialization is the scheme of common zeros of a tuple
$V\cap \,\pi ^{-1}_X(U)$
in the sense of the above-mentioned trivialization is the scheme of common zeros of a tuple
where
![]() $x_*$
are homogeneous coordinates on
$x_*$
are homogeneous coordinates on
![]() ${\mathbb P}^{M+k}$
and s runs through U.
${\mathbb P}^{M+k}$
and s runs through U.
Below (in §1), it will be clear that the open subset
![]() ${\cal F}$
from Theorem 0.1 is invariant under the action of the group
${\cal F}$
from Theorem 0.1 is invariant under the action of the group
![]() $\mathop {\mathrm {Aut}}{\mathbb P}^{M+k}$
. For that reason, the following definition makes sense.
$\mathop {\mathrm {Aut}}{\mathbb P}^{M+k}$
. For that reason, the following definition makes sense.
Definition 0.3. A fibration
![]() $V\subset X$
into complete intersections of type
$V\subset X$
into complete intersections of type
![]() $\underline {d}$
is a
$\underline {d}$
is a
![]() ${\cal F}$
-fibration, if for any trivialization of the bundle
${\cal F}$
-fibration, if for any trivialization of the bundle
![]() $\pi _X$
over an open set
$\pi _X$
over an open set
![]() $U\subset S$
, we have
$U\subset S$
, we have
![]() $\Phi _{U}(U)\subset {\cal F}$
.
$\Phi _{U}(U)\subset {\cal F}$
.
Obviously, if the inequality
 $$ \begin{align} \mathop{\mathrm{dim}} S\leqslant M-k+4+{M-\rho(k)+2 \choose 2} \end{align} $$
$$ \begin{align} \mathop{\mathrm{dim}} S\leqslant M-k+4+{M-\rho(k)+2 \choose 2} \end{align} $$
holds, then we may assume that V is a
![]() ${\cal F}$
-fibration. Set
${\cal F}$
-fibration. Set
![]() $\pi =\pi _X|_V$
. Now from Theorems 0.1 and 0.2 it is easy to obtain the third main result of the present paper.
$\pi =\pi _X|_V$
. Now from Theorems 0.1 and 0.2 it is easy to obtain the third main result of the present paper.
Theorem 0.3. Any
![]() ${\cal F}$
-fibration
${\cal F}$
-fibration
![]() $\pi \colon V\to S$
constructed above is a Fano-Mori fibre space. If the conditions (ii) and (iii) of Theorem 0.2 hold, then for every rationally connected fibre space
$\pi \colon V\to S$
constructed above is a Fano-Mori fibre space. If the conditions (ii) and (iii) of Theorem 0.2 hold, then for every rationally connected fibre space
![]() $V'/S'$
, every birational map
$V'/S'$
, every birational map
![]() $\chi \colon V\dashrightarrow V'$
is fibre-wise, and the fibre space
$\chi \colon V\dashrightarrow V'$
is fibre-wise, and the fibre space
![]() $V/ S$
itself is birationally rigid.
$V/ S$
itself is birationally rigid.
Example 0.1. Let
![]() $H_X$
be a numerically effective divisorial class on X, the restriction of which onto the fibre
$H_X$
be a numerically effective divisorial class on X, the restriction of which onto the fibre
![]() $\pi _X^{-1}(s)\cong {\mathbb P}^{M+k}$
is the class of a hyperplane. Let
$\pi _X^{-1}(s)\cong {\mathbb P}^{M+k}$
is the class of a hyperplane. Let
![]() $\Delta _1$
,…,
$\Delta _1$
,…,
![]() $\Delta _k$
be very ample classes on the base S. Let us construct a
$\Delta _k$
be very ample classes on the base S. Let us construct a
![]() ${\cal F}$
-fibration
${\cal F}$
-fibration
![]() $V/S$
as a complete intersection of k general divisors
$V/S$
as a complete intersection of k general divisors
where
![]() $G_i\in |d_i H_X+\pi _X^*\Delta _i|$
. Let us find out, when
$G_i\in |d_i H_X+\pi _X^*\Delta _i|$
. Let us find out, when
![]() $V/S$
satisfies the conditions (ii) and (iii) of Theorem 0.2. Write
$V/S$
satisfies the conditions (ii) and (iii) of Theorem 0.2. Write
Then we get
 $$ \begin{align*}K_V=\left.\left(-H_X+\pi^*_X\left(\Delta_X+\sum^k_{i=1}\Delta_i\right) \right)\right|_V. \end{align*} $$
$$ \begin{align*}K_V=\left.\left(-H_X+\pi^*_X\left(\Delta_X+\sum^k_{i=1}\Delta_i\right) \right)\right|_V. \end{align*} $$
It is easy to check that the inequality (3) in this case takes the form of the estimate
 $$ \begin{align*}\left(\left(\Delta_X+\sum^k_{i=1}\left(1-\frac{1}{d_i}\right)\Delta_i\right)\cdot \overline{C}\right)\geqslant \left(H_X^{M+k+1}\cdot \pi_X^{-1}(\overline{C})\right), \end{align*} $$
$$ \begin{align*}\left(\left(\Delta_X+\sum^k_{i=1}\left(1-\frac{1}{d_i}\right)\Delta_i\right)\cdot \overline{C}\right)\geqslant \left(H_X^{M+k+1}\cdot \pi_X^{-1}(\overline{C})\right), \end{align*} $$
where for the class
![]() $H_V$
, we took
$H_V$
, we took
![]() $H_X|_V$
. This inequality must be satisfied for every dense family
$H_X|_V$
. This inequality must be satisfied for every dense family
![]() $\overline {\cal C}\ni \overline {C}$
.
$\overline {\cal C}\ni \overline {C}$
.
Let us consider a very particular case, when
![]() $X={\mathbb P}^m\times {\mathbb P}^{M+k}$
and
$X={\mathbb P}^m\times {\mathbb P}^{M+k}$
and
![]() $G_i$
are divisors of bi-degree
$G_i$
are divisors of bi-degree
![]() $(m_i,d_i)$
,
$(m_i,d_i)$
,
![]() $i=1,\dots ,k$
. Taking for
$i=1,\dots ,k$
. Taking for
![]() $H_X$
the pullback on X of the class of a hyperplane in
$H_X$
the pullback on X of the class of a hyperplane in
![]() ${\mathbb P}^{M+k}$
, we get that the last inequality is equivalent to the numerical inequality
${\mathbb P}^{M+k}$
, we get that the last inequality is equivalent to the numerical inequality
 $$ \begin{align} \sum^k_{i=1}\left(1-\frac{1}{d_i}\right)m_i\geqslant m+1. \end{align} $$
$$ \begin{align} \sum^k_{i=1}\left(1-\frac{1}{d_i}\right)m_i\geqslant m+1. \end{align} $$
If it is satisfied and the dimension
![]() $m=\mathop {\mathrm {dim}} S$
satisfies the inequality (4), then the intersection
$m=\mathop {\mathrm {dim}} S$
satisfies the inequality (4), then the intersection
![]() $V=G_1\cap \dots \cap G_k$
of general (in the sense of Zariski topology) divisors of bi-degree
$V=G_1\cap \dots \cap G_k$
of general (in the sense of Zariski topology) divisors of bi-degree
![]() $(m_1,d_1),\dots ,(m_k,d_k)$
, fibred over
$(m_1,d_1),\dots ,(m_k,d_k)$
, fibred over
![]() $S={\mathbb P}^m$
, is a birationally rigid Fano-Mori fibre space, and every birational map of V onto the total space of a rationally connected fibre space is fibre-wise. The inequality (5) shows that this claim holds for almost all tuples
$S={\mathbb P}^m$
, is a birationally rigid Fano-Mori fibre space, and every birational map of V onto the total space of a rationally connected fibre space is fibre-wise. The inequality (5) shows that this claim holds for almost all tuples
![]() $(m_1,\dots ,m_k)\in {\mathbb Z}^k_+$
(except for finitely many of them) – that is, for almost all families of Fano-Mori fibre spaces – obtained by means of this construction. Note that the condition (5) is lose to a criterial one: if
$(m_1,\dots ,m_k)\in {\mathbb Z}^k_+$
(except for finitely many of them) – that is, for almost all families of Fano-Mori fibre spaces – obtained by means of this construction. Note that the condition (5) is lose to a criterial one: if
then the projection of V onto
![]() ${\mathbb P}^{M+k}$
defines on V a structure of a Fano-Mori fibre space (and a rationally connected fibre space), which is ‘transversal’ to the original structure
${\mathbb P}^{M+k}$
defines on V a structure of a Fano-Mori fibre space (and a rationally connected fibre space), which is ‘transversal’ to the original structure
![]() $\pi \colon V\to S$
(and is not fibre-wise), so that in this case,
$\pi \colon V\to S$
(and is not fibre-wise), so that in this case,
![]() $V/S$
is not birationally rigid.
$V/S$
is not birationally rigid.
0.4 The structure of the paper
The paper is organized in the following way. In §1, we produce the explicit local conditions defining the open subset
![]() ${\cal F}\subset {\cal P}$
. The proof of divisorial canonicity of a variety
${\cal F}\subset {\cal P}$
. The proof of divisorial canonicity of a variety
![]() $F\in {\cal F}$
(that is, of the inequality
$F\in {\cal F}$
(that is, of the inequality
![]() $\mathop {\mathrm {ct}}(F)\geqslant 1$
) is reduced in §1 to a number of technical facts that will be shown in the subsequent sections (§§3–7). In §2, we show Theorem 0.2.
$\mathop {\mathrm {ct}}(F)\geqslant 1$
) is reduced in §1 to a number of technical facts that will be shown in the subsequent sections (§§3–7). In §2, we show Theorem 0.2.
The proof of Theorem 0.1 consists of several pieces. The fact that the local conditions for the singularities that a variety
![]() $F\in {\cal F}$
can have (which are multi-quadratic singularities; see Subsection 1.2) guarantee that the variety F is factorial and its singularities are terminal is proven in §4, where we give a general definition of multi-quadratic singularities and study their properties. The estimate for the codimension of the complement
$F\in {\cal F}$
can have (which are multi-quadratic singularities; see Subsection 1.2) guarantee that the variety F is factorial and its singularities are terminal is proven in §4, where we give a general definition of multi-quadratic singularities and study their properties. The estimate for the codimension of the complement
![]() ${\cal P}\setminus {\cal F}$
(which is very important for constructing families of Fano-Mori fibre spaces, satisfying the assumptions of Theorem 0.2) is shown in §8. However, the main (and the hardest) part of the proof of Theorem 0.1 is to show that a variety
${\cal P}\setminus {\cal F}$
(which is very important for constructing families of Fano-Mori fibre spaces, satisfying the assumptions of Theorem 0.2) is shown in §8. However, the main (and the hardest) part of the proof of Theorem 0.1 is to show that a variety
![]() $F\in {\cal F}$
is divisorially canonical. We assume that for some effective divisor
$F\in {\cal F}$
is divisorially canonical. We assume that for some effective divisor
![]() $D\sim nH_F$
, the pair
$D\sim nH_F$
, the pair
![]() $(F,\frac {1}{n}D)$
is not canonical; that is, for some exceptional divisor E over F, the inequality
$(F,\frac {1}{n}D)$
is not canonical; that is, for some exceptional divisor E over F, the inequality
holds. Now we have to show that this assumption leads to a contradiction. In Subsections 1.3–1.6 it is shown how (using the inequalities for the multiplicity of subvarieties of the variety F at a given point, proven in §7) to obtain a contradiction in the case when a point of general position
![]() $o\in B$
, where B is the centre of E on F, either is non-singular on F or is a quadratic singularity. The hardest task is to obtain a contradiction when the point o is a multi-quadratic singularity of the variety F. A plan of solving this problem is given in Subsection 1.7, where we introduce the concept of a working triple and describe the procedure of constructing a sequence of subvarieties of the variety F, in which each subvariety is a hyperplane section of the previous one and the last subvariety delivers the desired contradiction.
$o\in B$
, where B is the centre of E on F, either is non-singular on F or is a quadratic singularity. The hardest task is to obtain a contradiction when the point o is a multi-quadratic singularity of the variety F. A plan of solving this problem is given in Subsection 1.7, where we introduce the concept of a working triple and describe the procedure of constructing a sequence of subvarieties of the variety F, in which each subvariety is a hyperplane section of the previous one and the last subvariety delivers the desired contradiction.
This program is realized in §3, where we study the properties of working triples; however, a number of key technical facts is only stated there – their proof is put off for a greater clarity of exposition. These key facts are shown in §§5, 6 (and the proof makes use of the facts on linear subspaces on complete intersections of quadrics, proven in Subsection 4.5).
Finally, in §7, we prove the estimates for the multiplicities of certain subvarieties of the variety F at given points in terms of the degrees of these subvarieties in
![]() ${\mathbb P}^{M+k}$
. Here we use the well-known technique of hypertangent divisors. For the purposes of our proof of Theorem 0.1, we have to somewhat modify this technique.
${\mathbb P}^{M+k}$
. Here we use the well-known technique of hypertangent divisors. For the purposes of our proof of Theorem 0.1, we have to somewhat modify this technique.
0.5 General remarks
The birational rigidity of Fano-Mori fibre spaces over a positive-dimensional base was one of the most important topics in birational geometry in the past 40 years. For its history and place in the context of the modern birational geometry of rationally connected varieties, see [Reference Pukhlikov2, Subsection 0.4]. Here we just mention a few recent papers in the areas that are close to the direction, to which the present paper belongs.
These areas are the birational rigidity, explicit birational geometry of Mori fibre spaces (including the studies of their groups of birational automorphisms and, wider, Sarkisov links), the rationality problem, computing and estimating the global canonical thresholds and, related to these problems, the theory of K-stability.
In the papers [Reference Krylov, Okada, Paemurru and Park4, Reference Abban and Krylov5, Reference Krylov6], important results on the birational rigidity and rigidity-type results for fibrations over
![]() ${\mathbb P}^1$
were obtained. The paper [Reference Stibitz7] links the Sarkisov program with the problem of estimating the canonical threshold of certain divisors on Fano varieties. The papers [Reference Abban and Okada8, Reference Krylov and Okada9] prove the stable non-rationality of very general conic bundles and fibrations into del Pezzo surfaces, respectively, over a higher-dimensional base. The problem of stable rationality for hypersurfaces of various bi-degrees in the products of projective spaces (see Example 0.1 above) is considered in [Reference Nicaise and Ottem10]. The theory of K-stability, which is on the border of birational geometry, is investigated in many papers (especially in the recent past) – in particular, see [Reference Stibitz and Zhuang11, Reference Zhuang12, Reference Cheltsov and Park13, Reference Cheltsov, Denisova and Fujita14]; we mentioned the papers that are the closest to the birational rigidity-type problems. Finally, there was a lot of development recently in the direction of applying the theory of Sarkisov links and relations between them to the study of the groups of birational automorphisms of such varieties that have a very large this group; see, for instance, [Reference Blanc and Yasinsky15, Reference Blanc, Lamy and Zimmermann16].
${\mathbb P}^1$
were obtained. The paper [Reference Stibitz7] links the Sarkisov program with the problem of estimating the canonical threshold of certain divisors on Fano varieties. The papers [Reference Abban and Okada8, Reference Krylov and Okada9] prove the stable non-rationality of very general conic bundles and fibrations into del Pezzo surfaces, respectively, over a higher-dimensional base. The problem of stable rationality for hypersurfaces of various bi-degrees in the products of projective spaces (see Example 0.1 above) is considered in [Reference Nicaise and Ottem10]. The theory of K-stability, which is on the border of birational geometry, is investigated in many papers (especially in the recent past) – in particular, see [Reference Stibitz and Zhuang11, Reference Zhuang12, Reference Cheltsov and Park13, Reference Cheltsov, Denisova and Fujita14]; we mentioned the papers that are the closest to the birational rigidity-type problems. Finally, there was a lot of development recently in the direction of applying the theory of Sarkisov links and relations between them to the study of the groups of birational automorphisms of such varieties that have a very large this group; see, for instance, [Reference Blanc and Yasinsky15, Reference Blanc, Lamy and Zimmermann16].
Getting back to the topic of this paper, we note that its immediate predecessor is [Reference Pukhlikov2], however, that paper investigates the non-canonical singularities, the centre of which is contained in the set of bi-quadratic points of the variety (from the technical viewpoint, this is the hardest part of the proof of divisorial canonicity), using the secant varieties of subvarieties of codimension 2 on an intersection of two quadrics. It is not possible to apply this approach to subvarieties of higher codimension on an intersection of
![]() $k\geqslant 3$
quadrics, and the present paper is based on a completely different construction (which applies to the bi-quadratic singularities, considered in [Reference Pukhlikov2], as well).
$k\geqslant 3$
quadrics, and the present paper is based on a completely different construction (which applies to the bi-quadratic singularities, considered in [Reference Pukhlikov2], as well).
The author is grateful to the members of Divisions of Algebraic Geometry and Algebra at Steklov Institute of Mathematics for the interest to his work, and also to the colleagues in Algebraic Geometry research group at the University of Liverpool for general support.
The author thanks the referee for their work on the manuscript and the helpful comments.
1 Fano complete intersections
In this section, we describe the local conditions defining the open subset
![]() ${\cal F}\subset {\cal P}$
(Subsections 1.2 and 1.4). For a complete intersection
${\cal F}\subset {\cal P}$
(Subsections 1.2 and 1.4). For a complete intersection
![]() $F\in {\cal F}$
, the proof of its divisorial canonicity is reduced to a number of technical claims, which will be shown later. A more detailed plan of the proof of Theorem 0.1 is given in Subsection 1.1.
$F\in {\cal F}$
, the proof of its divisorial canonicity is reduced to a number of technical claims, which will be shown later. A more detailed plan of the proof of Theorem 0.1 is given in Subsection 1.1.
1.1 A plan of the proof of Theorem 0.1
In order to prove Theorem 0.1, one has to give an explicit definition of the open set
![]() ${\cal F}\subset {\cal P}$
. This definition consists of two groups of conditions, which should be satisfied by the polynomials
${\cal F}\subset {\cal P}$
. This definition consists of two groups of conditions, which should be satisfied by the polynomials
![]() $f_1,\dots , f_k$
at every point
$f_1,\dots , f_k$
at every point
![]() $o\in {\mathbb P}^{M+k}$
at which they all vanish. The first group of conditions is about the singularities of the complete intersection
$o\in {\mathbb P}^{M+k}$
at which they all vanish. The first group of conditions is about the singularities of the complete intersection
![]() $F(\underline {f})$
: they can be quadratic or multi-quadratic of a rank bounded from below. The corresponding definitions and facts are given in Subsection 1.2. Assuming that the conditions of the first group are satisfied, we get that the scheme of common zeros of the polynomials
$F(\underline {f})$
: they can be quadratic or multi-quadratic of a rank bounded from below. The corresponding definitions and facts are given in Subsection 1.2. Assuming that the conditions of the first group are satisfied, we get that the scheme of common zeros of the polynomials
![]() $f_1,\dots , f_k$
is an irreducible reduced factorial variety
$f_1,\dots , f_k$
is an irreducible reduced factorial variety
![]() $F=F(\underline {f})\subset {\mathbb P}^{M+k}$
with terminal singularities, and so
$F=F(\underline {f})\subset {\mathbb P}^{M+k}$
with terminal singularities, and so
![]() $\mathop {\mathrm {Pic}} F={\mathbb Z} H_F$
and
$\mathop {\mathrm {Pic}} F={\mathbb Z} H_F$
and
![]() $K_F=-H_F$
, so that the question, Is it divisorially canonical?, makes sense.
$K_F=-H_F$
, so that the question, Is it divisorially canonical?, makes sense.
Assuming that F is not divisorially canonical, let us fix an effective divisor
![]() $D_F\sim n(D_F)H_F$
, where
$D_F\sim n(D_F)H_F$
, where
![]() $n(D_F)\geqslant 1$
, such that the pair
$n(D_F)\geqslant 1$
, such that the pair
 $$ \begin{align*}\left(F,\frac{1}{n(D_F)}D_F\right) \end{align*} $$
$$ \begin{align*}\left(F,\frac{1}{n(D_F)}D_F\right) \end{align*} $$
is not canonical; that is, there is an exceptional divisor E over F, satisfying the Noether-Fano inequality:
We have to show that the existence of such a divisor leads to a contradiction. Let
![]() $B\subset F$
be the centre of the exceptional divisor E on F. The information about the singularities of the varieties F makes it possible to easily exclude the option when
$B\subset F$
be the centre of the exceptional divisor E on F. The information about the singularities of the varieties F makes it possible to easily exclude the option when
![]() $\mathop {\mathrm {codim}}(B\subset F)=2$
. This is done in Subsection 1.3.
$\mathop {\mathrm {codim}}(B\subset F)=2$
. This is done in Subsection 1.3.
After that, in Subsection 1.4, we produce the second group of local conditions for the tuple of polynomials
![]() $\underline {f}\in {\cal F}$
: now they are the regularity conditions. Assuming that they are satisfied at every point
$\underline {f}\in {\cal F}$
: now they are the regularity conditions. Assuming that they are satisfied at every point
![]() $o\in F$
, we exclude the option
$o\in F$
, we exclude the option
![]() $B\not \subset \mathop {\mathrm {Sing}}F$
in Subsection 1.5, and in Subsection 1.6, the option that the point
$B\not \subset \mathop {\mathrm {Sing}}F$
in Subsection 1.5, and in Subsection 1.6, the option that the point
![]() $o\in B$
of general position is a quadratic singularity of F. In Subsection 1.7 we describe the procedure of excluding the multi-quadratic case, when the point
$o\in B$
of general position is a quadratic singularity of F. In Subsection 1.7 we describe the procedure of excluding the multi-quadratic case, when the point
![]() $o\in B$
of general position is a multi-quadratic singularity of the type
$o\in B$
of general position is a multi-quadratic singularity of the type
![]() $2^l$
,
$2^l$
,
![]() $l\in \{2,\dots ,k\}$
. This is the hardest part of the work, which is completed in the subsequent sections.
$l\in \{2,\dots ,k\}$
. This is the hardest part of the work, which is completed in the subsequent sections.
1.2 Multi-quadratic singularities
Let
![]() $o\in {\mathbb P}^{M+k}$
be a point at which
$o\in {\mathbb P}^{M+k}$
be a point at which
![]() $f_1,\dots ,f_k$
all vanish. Let us consider a system of affine coordinates
$f_1,\dots ,f_k$
all vanish. Let us consider a system of affine coordinates
![]() $z_*=(z_1,\dots ,z_{M+k})$
with the origin at the point o on an affine chart
$z_*=(z_1,\dots ,z_{M+k})$
with the origin at the point o on an affine chart
![]() ${\mathbb A}^{M+k}\subset {\mathbb P}^{M+k}$
, containing that point. Write down
${\mathbb A}^{M+k}\subset {\mathbb P}^{M+k}$
, containing that point. Write down
 $$ \begin{align*}\begin{array}{ccccc} f_1=f_{1,1}+f_{1,2}+ & \dots & + f_{1,d_1}, & &\\ f_2=f_{2,1}+f_{2,2}+ & \dots & & + f_{2,d_2}, & \\ & \dots & & &\\ f_k=f_{k,1}+f_{k,2}+ & \dots & & & +f_{k,d_k}, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccc} f_1=f_{1,1}+f_{1,2}+ & \dots & + f_{1,d_1}, & &\\ f_2=f_{2,1}+f_{2,2}+ & \dots & & + f_{2,d_2}, & \\ & \dots & & &\\ f_k=f_{k,1}+f_{k,2}+ & \dots & & & +f_{k,d_k}, \end{array} \end{align*} $$
where we use the same symbols
![]() $f_i$
for the non-homogeneous polynomials in
$f_i$
for the non-homogeneous polynomials in
![]() $z_*$
, corresponding to the original polynomials
$z_*$
, corresponding to the original polynomials
![]() $f_i$
, and
$f_i$
, and
![]() $f_{i,a}$
is a homogeneous polynomial of degree a in
$f_{i,a}$
is a homogeneous polynomial of degree a in
![]() $z_*$
. Obviously, if the linear forms
$z_*$
. Obviously, if the linear forms
![]() $f_{1,1},\dots ,f_{k,1}$
are linearly independent, then in a neighborhood of the point o, the scheme of common zeros of the polynomials
$f_{1,1},\dots ,f_{k,1}$
are linearly independent, then in a neighborhood of the point o, the scheme of common zeros of the polynomials
![]() $f_1,\dots ,f_k$
is a non-singular complete intersection of codimension k. In order to give the definition of a multi-quadratic singularity, we will need the concept of the rank of a tuple of quadratic forms.
$f_1,\dots ,f_k$
is a non-singular complete intersection of codimension k. In order to give the definition of a multi-quadratic singularity, we will need the concept of the rank of a tuple of quadratic forms.
Definition 1.1 [Reference Pukhlikov2].
The rank of the tuple of quadratic forms
![]() $q_1,\dots ,q_l$
in N variables is the number
$q_1,\dots ,q_l$
in N variables is the number
Obviously,
![]() $\mathop {\mathrm {rk}}(q_1,\dots ,q_l)\leqslant N$
. For that reason, in the sequel, the inequality
$\mathop {\mathrm {rk}}(q_1,\dots ,q_l)\leqslant N$
. For that reason, in the sequel, the inequality
![]() $\mathop {\mathrm {rk}}(q_*)\geqslant a$
means implicitly that the forms
$\mathop {\mathrm {rk}}(q_*)\geqslant a$
means implicitly that the forms
![]() $q_i$
depend on a sufficient
$q_i$
depend on a sufficient
![]() $(\geqslant a)$
number of variables.
$(\geqslant a)$
number of variables.
Take
![]() $l\in \{1,2,\dots ,k\}$
.
$l\in \{1,2,\dots ,k\}$
.
Definition 1.2. The tuple
![]() $\underline {f}$
has at the point o a multi-quadratic singularity of type
$\underline {f}$
has at the point o a multi-quadratic singularity of type
![]() $2^l$
of rank a, if the following conditions are satisfied:
$2^l$
of rank a, if the following conditions are satisfied:
-
•
 $\mathop {\mathrm {dim}}\langle f_{1,1},\dots ,f_{k,1}\rangle =k-l$
(and in order to simplify the notations, we assume that the forms are linearly independent),
$\mathop {\mathrm {dim}}\langle f_{1,1},\dots ,f_{k,1}\rangle =k-l$
(and in order to simplify the notations, we assume that the forms are linearly independent), $$ \begin{align*}f_{l+1},\dots, f_k \end{align*} $$
$$ \begin{align*}f_{l+1},\dots, f_k \end{align*} $$
-
• the rank of the tuple of quadratic forms
 $$ \begin{align*}f^*_{i,2}=f_{i,2}-\sum^k_{j=l+1}\lambda_{i,j}f_{j,2}, \end{align*} $$
$$ \begin{align*}f^*_{i,2}=f_{i,2}-\sum^k_{j=l+1}\lambda_{i,j}f_{j,2}, \end{align*} $$
 $i=1,\dots ,l$
, where
$i=1,\dots ,l$
, where
 $\lambda _{i,j}\in {\mathbb C}$
are defined by the equalities is equal to the number a.
$\lambda _{i,j}\in {\mathbb C}$
are defined by the equalities is equal to the number a. $$ \begin{align*}f_{i,1}=\sum^k_{j=l+1}\lambda_{i,j}f_{j,1}, \end{align*} $$
$$ \begin{align*}f_{i,1}=\sum^k_{j=l+1}\lambda_{i,j}f_{j,1}, \end{align*} $$
Now the first condition, defining the subset
![]() ${\cal F}\subset {\cal P}$
, is stated in the following way.
${\cal F}\subset {\cal P}$
, is stated in the following way.
(MQ1) For every point
![]() $o\in {\mathbb P}^{M+k}$
, such that
$o\in {\mathbb P}^{M+k}$
, such that
either the linear forms
![]() $f_{1,1},\dots ,f_{k,1}$
are linearly independent or
$f_{1,1},\dots ,f_{k,1}$
are linearly independent or
![]() $\underline {f}$
has at the point o a multi-quadratic singularity of type
$\underline {f}$
has at the point o a multi-quadratic singularity of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\in \{1,2,\dots ,k\}$
, of rank
$l\in \{1,2,\dots ,k\}$
, of rank
Theorem 1.1. Assume that
![]() $\underline {f}$
satisfies the condition (MQ1). Then the scheme of common zeros of the polynomials
$\underline {f}$
satisfies the condition (MQ1). Then the scheme of common zeros of the polynomials
![]() $f_1,\dots ,f_k$
is an irreducible reduced factorial variety F=F(f) – a complete intersection of codimension k with terminal singularities, and, moreover,
$f_1,\dots ,f_k$
is an irreducible reduced factorial variety F=F(f) – a complete intersection of codimension k with terminal singularities, and, moreover,
Proof is given in §4 (Subsections 4.1-4.3).
Assume that
![]() $\underline {f}$
satisfies the condition (MQ1). For a point
$\underline {f}$
satisfies the condition (MQ1). For a point
![]() $o\in F=F(\underline {f})$
, the symbol
$o\in F=F(\underline {f})$
, the symbol
![]() $T_oF$
stands for the subspace
$T_oF$
stands for the subspace
![]() $\{f_{1,1}=\dots =f_{k,1}=0\}\subset {\mathbb C}^{M+k}$
. For the proof of Theorem 0.1, we will need one more property of the tuple
$\{f_{1,1}=\dots =f_{k,1}=0\}\subset {\mathbb C}^{M+k}$
. For the proof of Theorem 0.1, we will need one more property of the tuple
![]() $\underline {f}$
, which we include in the definition of the subset
$\underline {f}$
, which we include in the definition of the subset
![]() ${\cal F}$
.
${\cal F}$
.
(MQ2) For any point
![]() $o\in F$
, which is a multi-quadratic of type
$o\in F$
, which is a multi-quadratic of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\geqslant 2$
, the rank of the tuple of quadratic forms
$l\geqslant 2$
, the rank of the tuple of quadratic forms
is at least
![]() $10k^2+8k+2\varepsilon (k)+5$
.
$10k^2+8k+2\varepsilon (k)+5$
.
The condition (MQ2) for multi-quadratic points of type
![]() $2^l$
with
$2^l$
with
![]() $l\geqslant 2$
implies the condition (MQ1) because the rank of a quadratic form, restricted to a hyperplane, drops at most by 2; however, for the convenience of references, we state the conditions (MQ1) and (MQ2) independently of each other. These conditions are used in the proof of Theorem 0.1 in different ways.
$l\geqslant 2$
implies the condition (MQ1) because the rank of a quadratic form, restricted to a hyperplane, drops at most by 2; however, for the convenience of references, we state the conditions (MQ1) and (MQ2) independently of each other. These conditions are used in the proof of Theorem 0.1 in different ways.
So every tuple
![]() $\underline {f}\in {\cal F}$
satisfies (MQ1) and (MQ2).
$\underline {f}\in {\cal F}$
satisfies (MQ1) and (MQ2).
1.3 Subvarieties of codimension 2
Following the plan, given in Subsection 1.1, let us fix an effective divisor
![]() $D_F\sim n(D_F)H_F$
,
$D_F\sim n(D_F)H_F$
,
![]() $n(D_F)\geqslant 1$
, such that the pair
$n(D_F)\geqslant 1$
, such that the pair
![]() $(F,\frac {1}{n(D_F)}D_F)$
is not canonical. By the symbol
$(F,\frac {1}{n(D_F)}D_F)$
is not canonical. By the symbol
 $$ \begin{align*} \mathop{\mathrm{CS}}\left(F,\frac{1}{n(D_F)}D_F\right), \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{CS}}\left(F,\frac{1}{n(D_F)}D_F\right), \end{align*} $$
we denote the union of the centres on F of all exceptional divisors over F, satisfying the Noether-Fano inequality (that is to say, of all non-canonical singularities of that pair). This is a closed subset of F. Let B be an irreducible component of maximal dimension of that set.
Proposition 1.1. The following inequality holds:
![]() $\mathop {\mathrm {codim}}(B\subset F)\geqslant 3$
.
$\mathop {\mathrm {codim}}(B\subset F)\geqslant 3$
.
Proof. Assume the converse:
![]() $\mathop {\mathrm {codim}}(B\subset F)=2$
. Then
$\mathop {\mathrm {codim}}(B\subset F)=2$
. Then
![]() $B\not \subset \mathop {\mathrm {Sing}}F$
. Moreover, let
$B\not \subset \mathop {\mathrm {Sing}}F$
. Moreover, let
![]() $P\subset {\mathbb P}^{M+k}$
be a general linear subspace of dimension
$P\subset {\mathbb P}^{M+k}$
be a general linear subspace of dimension
![]() $2k+2$
. Theorem 1.1 implies that
$2k+2$
. Theorem 1.1 implies that
![]() $P\cap \mathop {\mathrm {Sing}}F=\emptyset $
, so that
$P\cap \mathop {\mathrm {Sing}}F=\emptyset $
, so that
![]() $F\cap P$
is a non-singular complete intersection of type
$F\cap P$
is a non-singular complete intersection of type
![]() $\underline {d}$
in
$\underline {d}$
in
![]() $P\cong {\mathbb P}^{2k+2}$
. Furthermore, the pair
$P\cong {\mathbb P}^{2k+2}$
. Furthermore, the pair
 $$ \begin{align*}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
$$ \begin{align*}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
is not canonical, and the irreducible subvariety
![]() $B\cap P$
is an irreducible component of maximal dimension of the set
$B\cap P$
is an irreducible component of maximal dimension of the set
 $$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right), \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right), \end{align*} $$
so that (as
![]() $F\cap P$
is non-singular)
$F\cap P$
is non-singular)
However,
![]() $D_F|_{F\cap P}\sim n(D_F)H_{F\cap P}$
(where
$D_F|_{F\cap P}\sim n(D_F)H_{F\cap P}$
(where
![]() $H_{F\cap P}$
is the class of a hyperplane section of
$H_{F\cap P}$
is the class of a hyperplane section of
![]() $F\cap P$
), so that by [Reference Pukhlikov17, Proposition 3.6] or [Reference Suzuki18], we get a contradiction, proving the proposition. Q.E.D.
$F\cap P$
), so that by [Reference Pukhlikov17, Proposition 3.6] or [Reference Suzuki18], we get a contradiction, proving the proposition. Q.E.D.
1.4 Regularity conditions
In order to continue the proof of Theorem 0.1, we need a second group of conditions defining the set
![]() ${\cal F}$
. Let
${\cal F}$
. Let
![]() $o\in F$
be a point. We use the notations of Subsection 1.2. By the symbol
$o\in F$
be a point. We use the notations of Subsection 1.2. By the symbol
![]() $T_oF$
we denote the linear tangent space
$T_oF$
we denote the linear tangent space
and by the symbol
![]() ${\mathbb P}(T_oF)$
its projectivization. Let
${\mathbb P}(T_oF)$
its projectivization. Let
![]() ${\cal S}=(h_1,\dots ,h_M)$
be the sequence of homogeneous polynomials
${\cal S}=(h_1,\dots ,h_M)$
be the sequence of homogeneous polynomials
where
![]() $j\geqslant 2$
, placed in the lexicographic order:
$j\geqslant 2$
, placed in the lexicographic order:
![]() $(i_1,j_1)$
precedes
$(i_1,j_1)$
precedes
![]() $(i_2,j_2)$
, if
$(i_2,j_2)$
, if
![]() $j_1<j_2$
or
$j_1<j_2$
or
![]() $j_1=j_2$
, but
$j_1=j_2$
, but
![]() $i_1<i_2$
. By the symbol
$i_1<i_2$
. By the symbol
![]() ${\cal S}[-m]$
denote the sequence
${\cal S}[-m]$
denote the sequence
![]() ${\cal S}$
with the last m members removed. Finally, the symbol
${\cal S}$
with the last m members removed. Finally, the symbol
![]() ${\cal S}[-m]|_{\Pi }$
stands for the restriction of that sequence (that is, the restriction of each its member) onto a linear subspace
${\cal S}[-m]|_{\Pi }$
stands for the restriction of that sequence (that is, the restriction of each its member) onto a linear subspace
![]() $\Pi \subset {\mathbb P}(T_oF)$
. The regularity conditions depend on the type of the singularity
$\Pi \subset {\mathbb P}(T_oF)$
. The regularity conditions depend on the type of the singularity
![]() $o\in F$
.
$o\in F$
.
First, let the point
![]() $o\in F$
be non-singular, so that
$o\in F$
be non-singular, so that
![]() ${\mathbb P}(T_oF)\cong {\mathbb P}^{M-1}$
. In that case, the regularity condition is stated in the following way.
${\mathbb P}(T_oF)\cong {\mathbb P}^{M-1}$
. In that case, the regularity condition is stated in the following way.
(R1) The sequence
is regular for every subspace
![]() $\Pi \subset {\mathbb P}(T_oF)$
of codimension
$\Pi \subset {\mathbb P}(T_oF)$
of codimension
![]() $k+\varepsilon (k)-1$
.
$k+\varepsilon (k)-1$
.
The condition (R1) is assumed for every non-singular point
![]() $o\in F$
. It implies the following key fact.
$o\in F$
. It implies the following key fact.
Theorem 1.2. Let
![]() $P\subset {\mathbb P}^{M+k}$
be an arbitrary linear subspace of codimension
$P\subset {\mathbb P}^{M+k}$
be an arbitrary linear subspace of codimension
![]() $\leqslant k+ \varepsilon (k)-1$
. Then for every non-singular point
$\leqslant k+ \varepsilon (k)-1$
. Then for every non-singular point
![]() $o\in F\cap P$
and every prime divisor
$o\in F\cap P$
and every prime divisor
![]() $Y\sim n(Y)H_{F\cap P}$
on
$Y\sim n(Y)H_{F\cap P}$
on
![]() $F\cap P$
, the inequality
$F\cap P$
, the inequality
holds.
Proof is given in §7 (Subsections 7.1, 7.2).
Now let
![]() $o\in F$
be a quadratic singularity (this case corresponds to the value
$o\in F$
be a quadratic singularity (this case corresponds to the value
![]() $l=1$
in Definition 1.2). Here
$l=1$
in Definition 1.2). Here
![]() ${\mathbb P}(T_oF)\cong {\mathbb P}^M$
. In this case, the regularity condition is stated as follows.
${\mathbb P}(T_oF)\cong {\mathbb P}^M$
. In this case, the regularity condition is stated as follows.
(R2) The sequence
is regular for every hyperplane
![]() $\Pi \subset {\mathbb P}(T_oF)$
.
$\Pi \subset {\mathbb P}(T_oF)$
.
The condition (R2) is assumed for every quadratic singular point
![]() $o\in F$
and implies the following key fact.
$o\in F$
and implies the following key fact.
Theorem 1.3. Let
![]() $o\in F$
be a quadratic singularity and
$o\in F$
be a quadratic singularity and
![]() $W\ni o$
the section of F by a hyperplane that is not tangent to F at the point o, and
$W\ni o$
the section of F by a hyperplane that is not tangent to F at the point o, and
![]() $Y\sim n(Y)H_W$
a prime divisor on W. Then the following inequality holds:
$Y\sim n(Y)H_W$
a prime divisor on W. Then the following inequality holds:
Proof is given in §7 (Subsection 7.3).
(The symbol
![]() $H_W$
stands for the class of a hyperplane section of the variety W; the linear form, defining the hyperplane that cuts out W, is not a linear combination of the forms
$H_W$
stands for the class of a hyperplane section of the variety W; the linear form, defining the hyperplane that cuts out W, is not a linear combination of the forms
![]() $f_{1,1},\dots ,f_{k,1}$
.)
$f_{1,1},\dots ,f_{k,1}$
.)
Now let
![]() $o\in F$
be a multi-quadratic point of type
$o\in F$
be a multi-quadratic point of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\in \{2,\dots ,k\}$
. Here we will need two regularity conditions. In the first of them, the symbol
$l\in \{2,\dots ,k\}$
. Here we will need two regularity conditions. In the first of them, the symbol
![]() $T_oF$
means the projective closure of the linear subspace
$T_oF$
means the projective closure of the linear subspace
in
![]() ${\mathbb P}^{M+k}$
.
${\mathbb P}^{M+k}$
.
(R3.1) For every subspace
![]() $P\subset T_oF$
of codimension
$P\subset T_oF$
of codimension
![]() $\varepsilon (k)$
, containing the point o, the scheme of common zeros of the polynomials
$\varepsilon (k)$
, containing the point o, the scheme of common zeros of the polynomials
is an irreducible reduced subvariety of codimension
![]() $k+k_{\geqslant 3}$
in P, where
$k+k_{\geqslant 3}$
in P, where
Note that in the condition (R3.1), the homogeneous polynomials
![]() $f_{i,2}$
in the affine coordinates
$f_{i,2}$
in the affine coordinates
![]() $z_*$
are considered as quadratic forms in homogeneous coordinates on
$z_*$
are considered as quadratic forms in homogeneous coordinates on
![]() ${\mathbb P}^{M+k}$
.
${\mathbb P}^{M+k}$
.
In the second regularity condition for multi-quadratic points, the symbol
![]() $T_oF$
means a linear subspace in
$T_oF$
means a linear subspace in
![]() ${\mathbb C}^{M+k}$
.
${\mathbb C}^{M+k}$
.
(R3.2) For every linear subspace
![]() $\Pi \subset {\mathbb P}(T_oF)$
of codimension
$\Pi \subset {\mathbb P}(T_oF)$
of codimension
![]() $\varepsilon (k)$
, the sequence
$\varepsilon (k)$
, the sequence
is regular, where
![]() $m^*=\mathop {\mathrm {max}}\{\varepsilon (k)+4-l,0\}$
.
$m^*=\mathop {\mathrm {max}}\{\varepsilon (k)+4-l,0\}$
.
The conditions (R3.1) and (R3.2) are assumed for every multi-quadratic singular point
![]() $o\in F$
. They imply the following key inequality. In Theorem 1.4, stated below, the symbol
$o\in F$
. They imply the following key inequality. In Theorem 1.4, stated below, the symbol
![]() $T_oF$
stands for the projective closure of the embedded tangent space – that is, a linear subspace in
$T_oF$
stands for the projective closure of the embedded tangent space – that is, a linear subspace in
![]() ${\mathbb P}^{M+k}$
, containing the point o.
${\mathbb P}^{M+k}$
, containing the point o.
Theorem 1.4. Let
![]() $P\subset T_oF$
be an arbitrary linear subspace of codimension
$P\subset T_oF$
be an arbitrary linear subspace of codimension
![]() $\leqslant \varepsilon (k)$
and
$\leqslant \varepsilon (k)$
and
![]() $Y\ni o$
a prime divisor on
$Y\ni o$
a prime divisor on
![]() $F\cap P$
,
$F\cap P$
,
![]() $Y\sim n(Y)H_{F\cap P}$
. Then the following inequality holds:
$Y\sim n(Y)H_{F\cap P}$
. Then the following inequality holds:
Proof is given in §7 (Subsections 7.3).
(The symbol
![]() $H_{F\cap P}$
stands for the class of a hyperplane section of the variety
$H_{F\cap P}$
stands for the class of a hyperplane section of the variety
![]() $F\cap P$
; we will show below – see §4 – that
$F\cap P$
; we will show below – see §4 – that
![]() $F\cap P$
is an irreducible factorial complete intersection.)
$F\cap P$
is an irreducible factorial complete intersection.)
Summing up, let us give a complete definition of the subset
![]() ${\cal F}\subset {\cal P}$
: it consists of the tuples
${\cal F}\subset {\cal P}$
: it consists of the tuples
![]() $\underline {f}$
, satisfying the conditions (MQ1,2), the condition (R1) at every non-singular point
$\underline {f}$
, satisfying the conditions (MQ1,2), the condition (R1) at every non-singular point
![]() $o\in F(\underline {f})$
, the condition (R2) at every quadratic point
$o\in F(\underline {f})$
, the condition (R2) at every quadratic point
![]() $o\in F(\underline {f})$
and the conditions (R3.1,2) at every multi-quadratic point
$o\in F(\underline {f})$
and the conditions (R3.1,2) at every multi-quadratic point
![]() $o\in F(\underline {f})$
.
$o\in F(\underline {f})$
.
The inequality for the codimension of the complement
![]() ${\cal P}\setminus {\cal F}$
, given in Theorem 0.1, is shown in §8.
${\cal P}\setminus {\cal F}$
, given in Theorem 0.1, is shown in §8.
1.5 Exclusion of the non-singular case
We carry on with the proof of divisorial canonicity of the variety
![]() $F\in {\cal F}$
. In the notations of Subsection 1.3, assume that the point of general position
$F\in {\cal F}$
. In the notations of Subsection 1.3, assume that the point of general position
![]() $o\in B$
is a non-singular point of F. We know (Proposition 1.1) that
$o\in B$
is a non-singular point of F. We know (Proposition 1.1) that
![]() $\mathop {\mathrm {codim}}(B\subset F)\geqslant 3$
. Consider a general subspace
$\mathop {\mathrm {codim}}(B\subset F)\geqslant 3$
. Consider a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+3$
. Then
$k+3$
. Then
![]() $F\cap P$
is a non-singular three-dimensional variety, and the point o is a connected component of the set
$F\cap P$
is a non-singular three-dimensional variety, and the point o is a connected component of the set
 $$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
(if
![]() $\mathop {\mathrm {codim}}(B\subset F)\geqslant 4$
, then
$\mathop {\mathrm {codim}}(B\subset F)\geqslant 4$
, then
![]() $\mathop {\mathrm {CS}}$
can be replaced, by inversion of adjunction, by
$\mathop {\mathrm {CS}}$
can be replaced, by inversion of adjunction, by
![]() $\mathop {\mathrm {LCS}}$
); that is, outside the point o in a neighborhood of that point, the pair
$\mathop {\mathrm {LCS}}$
); that is, outside the point o in a neighborhood of that point, the pair
 $$ \begin{align} \left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align} $$
$$ \begin{align} \left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align} $$
is canonical. It is well known (see [Reference Pukhlikov19, Proposition 3] or [Reference Pukhlikov20, Chapter 7, Proposition 2.3]), and it follows from here that either the inequality
holds or on the exceptional divisor
![]() $E\cong {\mathbb P}^{M-1}$
of the blow-up
$E\cong {\mathbb P}^{M-1}$
of the blow-up
![]() $F^+\to F$
of the point o, there is a hyperplane
$F^+\to F$
of the point o, there is a hyperplane
![]() $\Theta \subset E$
(uniquely determined by the pair (6)), such that the inequality
$\Theta \subset E$
(uniquely determined by the pair (6)), such that the inequality
holds, where
![]() $D^+_F$
is the strict transform of
$D^+_F$
is the strict transform of
![]() $D_F$
on
$D_F$
on
![]() $F^+$
.
$F^+$
.
The first option is impossible as it contradicts Theorem 1.2. In the second case, denote by the symbol
![]() $|H-\Theta |$
the projectively k-dimensional linear system of hyperplane sections of F, a general element of which
$|H-\Theta |$
the projectively k-dimensional linear system of hyperplane sections of F, a general element of which
![]() $W\ni o$
is non-singular at the point o and satisfies the equality
$W\ni o$
is non-singular at the point o and satisfies the equality
The restriction
![]() $D_W=(D_F\circ W)$
is an effective divisor on W, and
$D_W=(D_F\circ W)$
is an effective divisor on W, and
![]() $n(D_W)=n(D_F)$
and the inequality
$n(D_W)=n(D_F)$
and the inequality
holds, which again contradicts Theorem 1.2. We have shown the following fact.
Proposition 1.2. The subvariety B is contained in the singular locus of F:
![]() $B\subset \mathop {\mathrm {Sing}} F$
.
$B\subset \mathop {\mathrm {Sing}} F$
.
1.6 Exclusion of the quadratic case
Again, let
![]() $o\in B$
be a point of general position.
$o\in B$
be a point of general position.
Proposition 1.3. The point o is a multi-quadratic singularity of type
![]() $2^l$
,
$2^l$
,
![]() $l\geqslant 2$
.
$l\geqslant 2$
.
Proof. Assume the converse: the point o is a quadratic singularity of F. Let
![]() $P\ni o$
be a general
$P\ni o$
be a general
![]() $(k+3)$
-dimensional linear subspace in
$(k+3)$
-dimensional linear subspace in
![]() ${\mathbb P}^{M+k}$
. By the condition (MQ1) and Theorem 1.1, the intersection
${\mathbb P}^{M+k}$
. By the condition (MQ1) and Theorem 1.1, the intersection
![]() $F\cap P$
is a three-dimensional variety with the unique singular point o, which is a non-degenerate quadratic singularity. This intersection can be constructed in two steps: first, we consider the intersection
$F\cap P$
is a three-dimensional variety with the unique singular point o, which is a non-degenerate quadratic singularity. This intersection can be constructed in two steps: first, we consider the intersection
![]() $F\cap P'$
with a general linear subspace
$F\cap P'$
with a general linear subspace
![]() $P'\subset {\mathbb P}^{M+k}$
,
$P'\subset {\mathbb P}^{M+k}$
,
![]() $P'\ni o$
of dimension
$P'\ni o$
of dimension
and after that the intersection with a general subspace
![]() $P\subset P'$
,
$P\subset P'$
,
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $(k+3)$
. Now we get the following: the pair
$(k+3)$
. Now we get the following: the pair
 $$ \begin{align*}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
$$ \begin{align*}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right) \end{align*} $$
is not log-canonical, but canonical outside the point o. Let us consider the blow-up
of the point o with the exceptional divisor
![]() ${\mathbb E}_P\cong {\mathbb P}^{k+2}$
and let
${\mathbb E}_P\cong {\mathbb P}^{k+2}$
and let
![]() $(F\cap P)^+\subset P^+$
be the strict transform of
$(F\cap P)^+\subset P^+$
be the strict transform of
![]() $F\cap P$
on
$F\cap P$
on
![]() $P^+$
, so that
$P^+$
, so that
![]() $(F\cap P)^+\to F\cap P$
is the blow-up of the quadratic singularity o with the exceptional divisor
$(F\cap P)^+\to F\cap P$
is the blow-up of the quadratic singularity o with the exceptional divisor
![]() $E_P=(F\cap P)^+\cap {\mathbb E}_P$
, which is a non-singular two-dimensional quadric in the three-dimensional subspace
$E_P=(F\cap P)^+\cap {\mathbb E}_P$
, which is a non-singular two-dimensional quadric in the three-dimensional subspace
![]() $\langle E_P\rangle \subset {\mathbb E}_P$
. Obviously,
$\langle E_P\rangle \subset {\mathbb E}_P$
. Obviously,
![]() $a(E_P, F\cap P)=1$
, so that, writing down
$a(E_P, F\cap P)=1$
, so that, writing down
and
![]() $D_P^+\sim n(D_F)H_{F\cap P}-\nu E_P$
(the strict transform of
$D_P^+\sim n(D_F)H_{F\cap P}-\nu E_P$
(the strict transform of
![]() $D_P$
on
$D_P$
on
![]() $(F\cap P)^+$
), we obtain two options:
$(F\cap P)^+$
), we obtain two options:
-
• either
 $\nu>2n(D_F)$
, so that
$\nu>2n(D_F)$
, so that
 $E_P$
is a non-log-canonical singularity of the pair
$E_P$
is a non-log-canonical singularity of the pair
 $(F\cap P,\frac {1}{n(D_F)} D_P)$
,
$(F\cap P,\frac {1}{n(D_F)} D_P)$
, -
• or
 $n(D_F)<\nu \leqslant 2n(D_F)$
, and then the closed set – the union of the centres of all non-log-canonical singularities of the original pair
$n(D_F)<\nu \leqslant 2n(D_F)$
, and then the closed set – the union of the centres of all non-log-canonical singularities of the original pair $$ \begin{align*}\mathop{\mathrm{LCS}}\left(\left(F\cap P,\frac{1}{n(D_F)} D_P\right), (F\cap P)^+\right) \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{LCS}}\left(\left(F\cap P,\frac{1}{n(D_F)} D_P\right), (F\cap P)^+\right) \end{align*} $$
 $(F\cap P,\frac {1}{n(D_F)} D_P)$
on
$(F\cap P,\frac {1}{n(D_F)} D_P)$
on
 $(F\cap P)^+$
– is a connected closed subset of the non-singular quadric
$(F\cap P)^+$
– is a connected closed subset of the non-singular quadric
 $E_P$
, which can be either a (possibly reducible) connected curve
$E_P$
, which can be either a (possibly reducible) connected curve
 $C_P\subset E_P$
or a point
$C_P\subset E_P$
or a point
 $x_P\in E_P$
.
$x_P\in E_P$
.
(It is well known – see, for instance, [Reference Pukhlikov20, Chapter 2, Proposition 3.7] – that the inequality
![]() $\nu \leqslant n(D_F$
) is impossible.) In the case
$\nu \leqslant n(D_F$
) is impossible.) In the case
![]() $\nu>2n(D_F)$
, we get
$\nu>2n(D_F)$
, we get
which contradicts Theorem 1.3, so that this case is impossible. Coming back to the original variety F, let us consider the blow-ups
![]() $\varphi _{\mathbb P}\colon ({\mathbb P}^{M+k})^+\to {\mathbb P}^{M+k}$
and
$\varphi _{\mathbb P}\colon ({\mathbb P}^{M+k})^+\to {\mathbb P}^{M+k}$
and
![]() $\varphi \colon F^+\to F$
of the point o, where
$\varphi \colon F^+\to F$
of the point o, where
![]() $F^+$
is identified with the strict transform of F on
$F^+$
is identified with the strict transform of F on
![]() $({\mathbb P}^{M+k})^+$
, with the exceptional divisors
$({\mathbb P}^{M+k})^+$
, with the exceptional divisors
![]() ${\mathbb E}$
and E, respectively, so that
${\mathbb E}$
and E, respectively, so that
![]() $E=F^+\cap {\mathbb E}$
is a quadratic hypersurface E in the subspace
$E=F^+\cap {\mathbb E}$
is a quadratic hypersurface E in the subspace
![]() $\langle E\rangle \subset {\mathbb E}$
of codimension
$\langle E\rangle \subset {\mathbb E}$
of codimension
![]() $(k+1)$
. By the condition for the rank (MQ1), the case of a point
$(k+1)$
. By the condition for the rank (MQ1), the case of a point
![]() $x_P\in E_P$
is impossible: in that case, the quadric E would contain a linear subspace of codimension 2 (with respect to E), which cannot happen. Now, arguing word for word as in [Reference Pukhlikov2, Subsection 3.2] and using [Reference Pukhlikov2, Theorem 3.1], we get that on the quadric E, there is a hyperplane section
$x_P\in E_P$
is impossible: in that case, the quadric E would contain a linear subspace of codimension 2 (with respect to E), which cannot happen. Now, arguing word for word as in [Reference Pukhlikov2, Subsection 3.2] and using [Reference Pukhlikov2, Theorem 3.1], we get that on the quadric E, there is a hyperplane section
![]() $\Lambda \subset E$
, such that
$\Lambda \subset E$
, such that
Taking the linear system
![]() $|H_F-\Lambda |$
(of the projective dimension
$|H_F-\Lambda |$
(of the projective dimension
![]() $(k-1)$
) of hyperplane sections of the variety F, a general divisor
$(k-1)$
) of hyperplane sections of the variety F, a general divisor
![]() $W\in |H_F-\Lambda |$
in which contains the point o and its strict transform
$W\in |H_F-\Lambda |$
in which contains the point o and its strict transform
![]() $W^+$
cuts out
$W^+$
cuts out
![]() $\Lambda $
on E (that is,
$\Lambda $
on E (that is,
![]() $W^+\cap E=\Lambda $
), we set
$W^+\cap E=\Lambda $
), we set
![]() $D_W=(D_F\circ W)$
and obtain the inequality
$D_W=(D_F\circ W)$
and obtain the inequality
which contradicts Theorem 1.3. This completes the proof of Proposition 1.3.
1.7 Exclusion of the multi-quadratic case
This is the hardest and the longest part of our work. Fix a point
![]() $o\in B$
of general position, which by what was proven is a multi-quadratic singularity of type
$o\in B$
of general position, which by what was proven is a multi-quadratic singularity of type
![]() $2^l$
, satisfying the conditions (MQ1,2). The pair
$2^l$
, satisfying the conditions (MQ1,2). The pair
![]() $(F,\frac {1}{n(D_F)}D_F)$
has a non-canonical singularity, the centre B of which is a component of the maximal dimension of the set
$(F,\frac {1}{n(D_F)}D_F)$
has a non-canonical singularity, the centre B of which is a component of the maximal dimension of the set
![]() $\mathop {\mathrm {CS}}(F,\frac {1}{n(D_F)}D_F)$
, so that in a neighborhood of the point o, this pair is canonical outside B. We will show that this is impossible. This will be done in a few steps, and now we describe the scheme of the proof and state the key intermediate claims.
$\mathop {\mathrm {CS}}(F,\frac {1}{n(D_F)}D_F)$
, so that in a neighborhood of the point o, this pair is canonical outside B. We will show that this is impossible. This will be done in a few steps, and now we describe the scheme of the proof and state the key intermediate claims.
Definition 1.3. A pair
![]() $[X,o]$
, where
$[X,o]$
, where
is an irreducible reduced factorial complete intersection of type
![]() $\underline {d}$
in the projective space
$\underline {d}$
in the projective space
![]() ${\mathbb P}(X)$
,
${\mathbb P}(X)$
,
![]() $\mathop {\mathrm {dim}}X=N(X)-k\geqslant 3$
, and
$\mathop {\mathrm {dim}}X=N(X)-k\geqslant 3$
, and
![]() $o\in X$
is a point, is called a complete intersection with a marked point or, for brevity, a marked complete intersection of level
$o\in X$
is a point, is called a complete intersection with a marked point or, for brevity, a marked complete intersection of level
![]() $(l_X,c_X)$
), where
$(l_X,c_X)$
), where
![]() $l_X$
,
$l_X$
,
![]() $c_X$
are positive integers, satisfying the inequalities
$c_X$
are positive integers, satisfying the inequalities
if the following conditions are satisfied:
(MC1) the inequality
holds,
(MC2) the point
![]() $o\in X$
is a multi-quadratic singularity of type
$o\in X$
is a multi-quadratic singularity of type
![]() $2^{l_X}$
, the rank of which satisfies the inequality
$2^{l_X}$
, the rank of which satisfies the inequality
(MC3) the non-singular part
![]() $X\setminus \mathop {\mathrm {Sing}}X$
of the variety X satisfies the condition of divisorial canonicity,
$X\setminus \mathop {\mathrm {Sing}}X$
of the variety X satisfies the condition of divisorial canonicity,
that is, for every effective divisor
![]() $A\sim aH_X$
, we have
$A\sim aH_X$
, we have
![]() $\mathop {\mathrm {CS}}(X,\frac {1}{a}A)\subset \mathop {\mathrm {Sing}}X$
.
$\mathop {\mathrm {CS}}(X,\frac {1}{a}A)\subset \mathop {\mathrm {Sing}}X$
.
The non-singular set of integers
is called the admissible set of the marked complete intersection
![]() $[X,o]$
.
$[X,o]$
.
Remark 1.1. (i) Since
![]() $X\subset {\mathbb P}(X)$
is a complete intersection, the factoriality of the variety X follows from Grothendieck’s theorem [Reference Call and Lyubeznik21] by the condition (MC1). For that reason,
$X\subset {\mathbb P}(X)$
is a complete intersection, the factoriality of the variety X follows from Grothendieck’s theorem [Reference Call and Lyubeznik21] by the condition (MC1). For that reason,
![]() $\mathop {\mathrm {Pic}}X={\mathbb Z}H_X$
, where
$\mathop {\mathrm {Pic}}X={\mathbb Z}H_X$
, where
![]() $H_X$
is the class of a hyperplane section.
$H_X$
is the class of a hyperplane section.
(ii) By (MC1), for every
![]() $m\leqslant k+c_X-1$
and a general subspace
$m\leqslant k+c_X-1$
and a general subspace
![]() $P\ni o$
of dimension m in
$P\ni o$
of dimension m in
![]() ${\mathbb P}(X)$
, the point o is the only singularity of the variety
${\mathbb P}(X)$
, the point o is the only singularity of the variety
![]() $X\cap P$
.
$X\cap P$
.
(iii) Let
![]() ${\mathbb P}(X)^+\to {\mathbb P}(X)$
be the blow-up of the point o with the exceptional divisor
${\mathbb P}(X)^+\to {\mathbb P}(X)$
be the blow-up of the point o with the exceptional divisor
![]() ${\mathbb E}_X\cong {\mathbb P}^{N(X)-1}$
. The strict transform
${\mathbb E}_X\cong {\mathbb P}^{N(X)-1}$
. The strict transform
![]() $X^+\subset {\mathbb P}(X)^+$
is the result of blowing up the point o on X with the exceptional divisor
$X^+\subset {\mathbb P}(X)^+$
is the result of blowing up the point o on X with the exceptional divisor
![]() $E_X=X^+\cap {\mathbb E}_X$
. Obviously,
$E_X=X^+\cap {\mathbb E}_X$
. Obviously,
![]() $E_X$
is an irreducible reduced non-degenerate complete intersection of
$E_X$
is an irreducible reduced non-degenerate complete intersection of
![]() $l_X$
quadrics in a linear subspace of codimension
$l_X$
quadrics in a linear subspace of codimension
![]() $(k-l_X)$
in
$(k-l_X)$
in
![]() ${\mathbb E}_X$
(this follows from (MC2); see Proposition 1.4).
${\mathbb E}_X$
(this follows from (MC2); see Proposition 1.4).
Proposition 1.4. The following inequality holds:
Proof. See in §4 (Subsection 4.2; by the condition (MC2) the claim of the proposition follows from Proposition 4.2, (ii)).
Remark 1.2. Proposition 1.4 implies the estimate
Therefore, for every
![]() $m\leqslant k+c_X$
and a general subspace
$m\leqslant k+c_X$
and a general subspace
![]() $P\ni o$
of dimension m in
$P\ni o$
of dimension m in
![]() ${\mathbb P}(X)$
, the strict transform
${\mathbb P}(X)$
, the strict transform
![]() $P^+\subset {\mathbb P}(X)^+$
does not meet the set
$P^+\subset {\mathbb P}(X)^+$
does not meet the set
![]() $\mathop {\mathrm {Sing}}E_X$
, since
$\mathop {\mathrm {Sing}}E_X$
, since
![]() $P^+\cap {\mathbb E}_X$
is a general linear subspace of dimension
$P^+\cap {\mathbb E}_X$
is a general linear subspace of dimension
![]() $m-1\leqslant k+c_X-1$
in
$m-1\leqslant k+c_X-1$
in
![]() ${\mathbb E}_X$
. Therefore, for
${\mathbb E}_X$
. Therefore, for
![]() $m=k+c_X$
an isolated, and for
$m=k+c_X$
an isolated, and for
![]() $m\leqslant k+c_X-1$
the unique singularity o of the variety
$m\leqslant k+c_X-1$
the unique singularity o of the variety
![]() $X\cap P$
is resolved by the blow-up of that point, and moreover, the exceptional divisor
$X\cap P$
is resolved by the blow-up of that point, and moreover, the exceptional divisor
of that blow-up is a non-singular complete intersection of
![]() $l_X$
quadrics in the linear subspace of codimension
$l_X$
quadrics in the linear subspace of codimension
![]() $(k-l_X)$
in
$(k-l_X)$
in
![]() ${\mathbb E}_{X\cap P}=P^+\cap {\mathbb E}_X$
. The discrepancy of that exceptional divisor is
${\mathbb E}_{X\cap P}=P^+\cap {\mathbb E}_X$
. The discrepancy of that exceptional divisor is
so that for
![]() $m=k+l_X+3$
, we have
$m=k+l_X+3$
, we have
![]() $a(E_{X\cap P})=2$
. The meaning of the lower end of the admissible set is in that equality.
$a(E_{X\cap P})=2$
. The meaning of the lower end of the admissible set is in that equality.
In the following definition, we use the notations of Remarks 1.1 and 1.2. We continue to consider a marked complete intersection
![]() $[X,o]$
of level
$[X,o]$
of level
![]() $(l_X,c_X)$
.
$(l_X,c_X)$
.
Definition 1.4. A triple
![]() $(X,D,o)$
, where
$(X,D,o)$
, where
![]() $D\sim n(D)H_X$
is an effective divisor on X,
$D\sim n(D)H_X$
is an effective divisor on X,
![]() $n(D)\geqslant 1$
, is called a working triple, if for a general subspace
$n(D)\geqslant 1$
, is called a working triple, if for a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+c_X-1$
in
$k+c_X-1$
in
![]() ${\mathbb P}(X)$
, the pair
${\mathbb P}(X)$
, the pair
 $$ \begin{align} \left(X\cap P,\frac{1}{n(D)}D|_{X\cap P}\right) \end{align} $$
$$ \begin{align} \left(X\cap P,\frac{1}{n(D)}D|_{X\cap P}\right) \end{align} $$
is not log-canonical at the point o.
Remark 1.3. Since the point o is the unique singularity of the variety
![]() $X\cap P$
, and by (MC3) the pair (7) is canonical outside the point o, there is a non-log-canonical singularity of that pair, the centre of which on
$X\cap P$
, and by (MC3) the pair (7) is canonical outside the point o, there is a non-log-canonical singularity of that pair, the centre of which on
![]() $X\cap P$
is precisely the point o. By inversion of adjunction, the same is true for a general subspace
$X\cap P$
is precisely the point o. By inversion of adjunction, the same is true for a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $m\leqslant k+c_X-2$
.
$m\leqslant k+c_X-2$
.
Let us introduce one more notation. For the strict transform
![]() $D^+$
of the divisor D on
$D^+$
of the divisor D on
![]() $X^+$
, write
$X^+$
, write
(in order to simplify the notations, the pullback of the divisorial class
![]() $H_X$
on
$H_X$
on
![]() $X^+$
is denoted by the same symbol
$X^+$
is denoted by the same symbol
![]() $H_X$
). Respectively, for a general subspace
$H_X$
). Respectively, for a general subspace
![]() $P\ni o$
in
$P\ni o$
in
![]() ${\mathbb P}(X)$
of dimension
${\mathbb P}(X)$
of dimension
![]() $m\leqslant k+c_X-1$
, we have
$m\leqslant k+c_X-1$
, we have
and
where
![]() $H_{X\cap P}=H_X|_{X\cap P}$
is the class of a hyperplane section of the variety
$H_{X\cap P}=H_X|_{X\cap P}$
is the class of a hyperplane section of the variety
![]() $X\cap P\subset P\cong {\mathbb P}^m$
.
$X\cap P\subset P\cong {\mathbb P}^m$
.
Proposition 1.5. Assume that
![]() $c_X\geqslant 2l_X+4$
. Then the inequality
$c_X\geqslant 2l_X+4$
. Then the inequality
![]() $\nu (D)>n(D)$
holds.
$\nu (D)>n(D)$
holds.
Proof is given in §3 (Subsection 3.2).
Let us come back to the task of excluding the multi-quadratic case. Recall that
![]() $F\in {\cal F}$
, so that we can use the conditions (MQ1,2) and the statement of Theorem 1.4. We fix a point of general position
$F\in {\cal F}$
, so that we can use the conditions (MQ1,2) and the statement of Theorem 1.4. We fix a point of general position
![]() $o\in B$
, where B is an irreducible component of the maximal dimension of the closed set
$o\in B$
, where B is an irreducible component of the maximal dimension of the closed set
![]() $\mathop {\mathrm {CS}}(F,\frac {1}{n(D_F)}D_F)$
.
$\mathop {\mathrm {CS}}(F,\frac {1}{n(D_F)}D_F)$
.
Proposition 1.6. The pair
![]() $[F,o]$
is a marked complete intersection of level
$[F,o]$
is a marked complete intersection of level
![]() $(l,c_F)$
, where
$(l,c_F)$
, where
![]() $c_F=4k+2\varepsilon (k)$
, and
$c_F=4k+2\varepsilon (k)$
, and
![]() $(F,D_F,o)$
is a working triple.
$(F,D_F,o)$
is a working triple.
Proof is given in §3 (Subsection 3.1).
Assume now that
![]() $l\leqslant k-1$
. The symbol
$l\leqslant k-1$
. The symbol
![]() $T_oF$
stands again for a subspace of codimension
$T_oF$
stands again for a subspace of codimension
![]() $(k-l)$
of the projective space
$(k-l)$
of the projective space
![]() ${\mathbb P}^{M+k}$
. Set
${\mathbb P}^{M+k}$
. Set
This is subvariety of codimension
![]() $(k-l)$
in F and a complete intersection of type
$(k-l)$
in F and a complete intersection of type
![]() $\underline {d}$
in
$\underline {d}$
in
![]() ${\mathbb P}(T)=T_oF$
.
${\mathbb P}(T)=T_oF$
.
Remark 1.4. Let us state here two well-known facts which we will use many times in the sequel: when a quadratic form is restricted to a hyperplane, its rank either remains the same or drops by 1 or 2; when a complete intersection in the projective space is intersected with a hyperplane, the codimension of its singular locus either remains the same or drops by 1 or 2 (for a proof of the second claim, see [Reference Iskovskikh and Pukhlikov22] or [Reference Pukhlikov23]).
If
![]() $l=k$
, then for uniformity of notations, we set
$l=k$
, then for uniformity of notations, we set
![]() $T=F$
.
$T=F$
.
Proposition 1.7. The pair
![]() $[T,o]$
is a marked complete intersection of level
$[T,o]$
is a marked complete intersection of level
![]() $(k,c_T)$
, where
$(k,c_T)$
, where
![]() $c_T=2k+2\varepsilon (k)+4$
. There is an effective divisor
$c_T=2k+2\varepsilon (k)+4$
. There is an effective divisor
![]() $D_T\sim n(D_T)H_T$
on T, such that
$D_T\sim n(D_T)H_T$
on T, such that
![]() $(T,D_T,o)$
is a working triple.
$(T,D_T,o)$
is a working triple.
Proof is given in §3 (Subsection 3.4).
Proposition 1.5 (taking into account Remark 1.4) implies that
![]() $\nu (D_T)>n(D_T)$
. Now the main stage in the exclusion of the multi-quadratic case (and thus in the proof of Theorem 0.1) is given by the following claim.
$\nu (D_T)>n(D_T)$
. Now the main stage in the exclusion of the multi-quadratic case (and thus in the proof of Theorem 0.1) is given by the following claim.
Proposition 1.8. There is a sequence of marked complete intersections
where
![]() $a\leqslant \varepsilon (k)$
and
$a\leqslant \varepsilon (k)$
and
![]() ${\mathbb P}(R_{i+1})$
is a hyperplane in
${\mathbb P}(R_{i+1})$
is a hyperplane in
![]() ${\mathbb P}(R_{i})$
, containing the point o, and of effective divisors
${\mathbb P}(R_{i})$
, containing the point o, and of effective divisors
![]() $D_i\sim n(D_i)H_{R_i}$
on
$D_i\sim n(D_i)H_{R_i}$
on
![]() $R_i$
,
$R_i$
,
![]() $n(D_i)\geqslant 1$
, such that
$n(D_i)\geqslant 1$
, such that
![]() $D_0=D_T$
and
$D_0=D_T$
and
are working triples, and moreover, for every
![]() $i=0,\dots ,a-1$
, the inequality
$i=0,\dots ,a-1$
, the inequality
 $$ \begin{align*}2-\frac{\nu(D_{i+1})}{n(D_{i+1})}<\frac{1}{1+\frac{1}{k}}\left( 2-\frac{\nu(D_i)}{n(D_i)}\right) \end{align*} $$
$$ \begin{align*}2-\frac{\nu(D_{i+1})}{n(D_{i+1})}<\frac{1}{1+\frac{1}{k}}\left( 2-\frac{\nu(D_i)}{n(D_i)}\right) \end{align*} $$
holds and
![]() $\nu (D_a)>\frac 32 n(D_a)$
.
$\nu (D_a)>\frac 32 n(D_a)$
.
Proof is given in §3 (Subsection 3.5) and §5.
Now let us complete the exclusion of the multi-quadratic case. The variety
![]() $R_a$
is a section of
$R_a$
is a section of
![]() $T=F\cap T_oF$
by a subspace of codimension
$T=F\cap T_oF$
by a subspace of codimension
![]() $\leqslant \varepsilon (k)$
, containing the point o, and
$\leqslant \varepsilon (k)$
, containing the point o, and
![]() $D_a$
is an effective divisor on
$D_a$
is an effective divisor on
![]() $R_a$
, satisfying the inequality
$R_a$
, satisfying the inequality
This contradicts Theorem 1.4.
The contradiction completes the proof of divisorial canonicity of the variety
![]() $F\in {\cal F}$
.
$F\in {\cal F}$
.
2 Fano-Mori fibre spaces
In this section, we prove Theorem 0.2. In Subsection 2.1, we associate with a birational map
![]() $\chi \colon V\dashrightarrow V'$
a mobile linear system
$\chi \colon V\dashrightarrow V'$
a mobile linear system
![]() $\Sigma $
on V and state the key Theorem 2.1 about this system. In Subsection 2.2, we construct a fibre-wise birational modification of the fibre space
$\Sigma $
on V and state the key Theorem 2.1 about this system. In Subsection 2.2, we construct a fibre-wise birational modification of the fibre space
![]() $V/S$
for the system
$V/S$
for the system
![]() $\Sigma $
. In Subsection 2.3, we consider a mobile algebraic family of irreducible curves
$\Sigma $
. In Subsection 2.3, we consider a mobile algebraic family of irreducible curves
![]() ${\cal C}$
on V and use it to prove (in Subsection 2.4) Theorem 2.1, which implies the first claim of Theorem 0.2 (that
${\cal C}$
on V and use it to prove (in Subsection 2.4) Theorem 2.1, which implies the first claim of Theorem 0.2 (that
![]() $\chi $
is fibre-wise). In Subsection 2.5, we prove the birational rigidity of the fibre space
$\chi $
is fibre-wise). In Subsection 2.5, we prove the birational rigidity of the fibre space
![]() $V/S$
.
$V/S$
.
2.1 The mobile linear system
 $\Sigma $
$\Sigma $
Assume that the Fano-Mori fibre space
![]() $\pi \colon V\to S$
satisfies all conditions of Theorem 0.2. Fix a fibre space
$\pi \colon V\to S$
satisfies all conditions of Theorem 0.2. Fix a fibre space
![]() $\pi '\colon V'\to S'$
that belongs to one of the two classes: either the class of rationally connected fibre spaces (and then we say that the rationally connected case is being considered) or the class of Mori fibre spaces in the sense of Subsection 0.2 (and then we say that the case of a Mori fibre space is being considered). We will study both cases simultaneously.
$\pi '\colon V'\to S'$
that belongs to one of the two classes: either the class of rationally connected fibre spaces (and then we say that the rationally connected case is being considered) or the class of Mori fibre spaces in the sense of Subsection 0.2 (and then we say that the case of a Mori fibre space is being considered). We will study both cases simultaneously.
In the rationally connected case, let
![]() $Y'\in \mathop {\mathrm {Pic}}S'$
be a very ample class. Set
$Y'\in \mathop {\mathrm {Pic}}S'$
be a very ample class. Set
where
![]() $m=0$
. This is a mobile complete linear system on
$m=0$
. This is a mobile complete linear system on
![]() $V'$
(it defines the morphism
$V'$
(it defines the morphism
![]() $\pi '$
).
$\pi '$
).
In the case of a Mori fibre space, let
be a complete linear system on
![]() $V'$
, where
$V'$
, where
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $Y'$
is a very ample divisorial class on
$Y'$
is a very ample divisorial class on
![]() $S'$
, and moreover, for
$S'$
, and moreover, for
![]() $m\geqslant 1$
, the system
$m\geqslant 1$
, the system
![]() $\Sigma '$
is very ample.
$\Sigma '$
is very ample.
In both cases, set
to be the strict transform of
![]() $\Sigma '$
on V with respect to the birational map
$\Sigma '$
on V with respect to the birational map
![]() $\chi \colon V\dashrightarrow V'$
. Note that if
$\chi \colon V\dashrightarrow V'$
. Note that if
![]() $m=0$
and
$m=0$
and
![]() $n=0$
, then by construction of these linear systems, the map
$n=0$
, then by construction of these linear systems, the map
![]() $\chi $
is fibre-wise.
$\chi $
is fibre-wise.
Theorem 2.1. The following inequality holds:
![]() $n\leqslant m$
.
$n\leqslant m$
.
Proof. Assume the converse:
![]() $n>m$
. In particular, if
$n>m$
. In particular, if
![]() $m=0$
, then
$m=0$
, then
![]() $\chi $
is not fibre-wise. Let us show that this assumption leads to a contradiction.
$\chi $
is not fibre-wise. Let us show that this assumption leads to a contradiction.
2.2 A fibre-wise birational modification of the fibre space
 $V/S$
$V/S$
Let
![]() $\sigma _S\colon S^+\to S$
be a composition of blow-ups with non-singular centres,
$\sigma _S\colon S^+\to S$
be a composition of blow-ups with non-singular centres,
where
![]() $\sigma _{S,i+1}\colon S_{i+1}\to S_i$
blows up a non-singular subvariety
$\sigma _{S,i+1}\colon S_{i+1}\to S_i$
blows up a non-singular subvariety
![]() $Z_{S,i}\subset S_i$
. Set
$Z_{S,i}\subset S_i$
. Set
![]() $V_i=V\times _SS_i$
and
$V_i=V\times _SS_i$
and
![]() $\pi _i\colon V_i\to S_i$
; by the assumption on the stability with respect to birational modifications of the base,
$\pi _i\colon V_i\to S_i$
; by the assumption on the stability with respect to birational modifications of the base,
![]() $V_i/S_i$
is a Fano-Mori fibre space. Obviously,
$V_i/S_i$
is a Fano-Mori fibre space. Obviously,
is the result of the blow-up
![]() $\sigma _{i+1}\colon V_{i+1}\to V_i$
of the subvariety
$\sigma _{i+1}\colon V_{i+1}\to V_i$
of the subvariety
![]() $Z_i=\pi ^{-1}_i(Z_{S,i})\subset V_i$
. Therefore, we get the commutative diagram
$Z_i=\pi ^{-1}_i(Z_{S,i})\subset V_i$
. Therefore, we get the commutative diagram
 $$ \begin{align*}\begin{array}{ccccccccccccccc} V^+ & = & V_N & \stackrel{\sigma_N}{\to} & \dots & \to & V_{i+1} & \stackrel{\sigma_{i+1}}{\to} & V_i & \to & \dots & \stackrel{\sigma_1}{\to} & V_0 & = & V \\ & & \downarrow & & \dots & & \downarrow & & \downarrow & & \dots & & \downarrow & & \\ S^+ & = & S_N & \stackrel{\sigma_{S,N}}{\to} & \dots & \to & S_{i+1} & \stackrel{\sigma_{S,i+1}}{\to} & S_i & \to & \dots & \stackrel{\sigma_{S,1}}{\to} & S_0 & = & S, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccccccccccccc} V^+ & = & V_N & \stackrel{\sigma_N}{\to} & \dots & \to & V_{i+1} & \stackrel{\sigma_{i+1}}{\to} & V_i & \to & \dots & \stackrel{\sigma_1}{\to} & V_0 & = & V \\ & & \downarrow & & \dots & & \downarrow & & \downarrow & & \dots & & \downarrow & & \\ S^+ & = & S_N & \stackrel{\sigma_{S,N}}{\to} & \dots & \to & S_{i+1} & \stackrel{\sigma_{S,i+1}}{\to} & S_i & \to & \dots & \stackrel{\sigma_{S,1}}{\to} & S_0 & = & S, \end{array} \end{align*} $$
where the vertical arrows
![]() $\pi \colon V_i\to S_i$
are Fano-Mori fibre spaces. The symbol
$\pi \colon V_i\to S_i$
are Fano-Mori fibre spaces. The symbol
![]() $\Sigma ^i$
stands for the strict transform of the system
$\Sigma ^i$
stands for the strict transform of the system
![]() $\Sigma $
on
$\Sigma $
on
![]() $V_i$
,
$V_i$
,
![]() $\Sigma ^+=\Sigma ^N$
. In these notations, let us consider a sequence of blow-ups
$\Sigma ^+=\Sigma ^N$
. In these notations, let us consider a sequence of blow-ups
![]() $\sigma _{S,*}$
such that for every
$\sigma _{S,*}$
such that for every
![]() $i=0,1,\dots ,N-1$
,
$i=0,1,\dots ,N-1$
,
and the base set of the system
![]() $\Sigma ^+$
contains entirely no fibre
$\Sigma ^+$
contains entirely no fibre
![]() $\pi ^{-1}_+(s_+)$
, where
$\pi ^{-1}_+(s_+)$
, where
![]() $s_+\in S^+$
and
$s_+\in S^+$
and
![]() $\pi _+=\pi _N$
. (If this is true already for the original system
$\pi _+=\pi _N$
. (If this is true already for the original system
![]() $\Sigma $
, then we set
$\Sigma $
, then we set
![]() $\sigma _S=\mathop {\mathrm {id}}_S$
,
$\sigma _S=\mathop {\mathrm {id}}_S$
,
![]() $S^+=S$
and
$S^+=S$
and
![]() $V^+=V$
, and there is no need to make any blow-ups; but we will soon see that this case is impossible.)
$V^+=V$
, and there is no need to make any blow-ups; but we will soon see that this case is impossible.)
By the assumptions on the fibre space
![]() $V/S$
, the fibre
$V/S$
, the fibre
![]() $\pi ^{-1}_+(s_+)$
is isomorphic to the fibre
$\pi ^{-1}_+(s_+)$
is isomorphic to the fibre
![]() $F_s=\pi ^{-1}(s)$
of the original fibre space, where
$F_s=\pi ^{-1}(s)$
of the original fibre space, where
![]() $s=\sigma _S(s_+)$
. Let
$s=\sigma _S(s_+)$
. Let
![]() ${\cal T}$
be the set of all prime
${\cal T}$
be the set of all prime
![]() $\sigma _S$
-exceptional divisors on
$\sigma _S$
-exceptional divisors on
![]() $S^+$
. We get
$S^+$
. We get
 $$ \begin{align*}\Sigma^+\subset\left|-n\sigma^*K_V+\pi^*_+\left(\sigma^*_SY-\sum_{T\in{\cal T}}b_TT\right)\right|= \end{align*} $$
$$ \begin{align*}\Sigma^+\subset\left|-n\sigma^*K_V+\pi^*_+\left(\sigma^*_SY-\sum_{T\in{\cal T}}b_TT\right)\right|= \end{align*} $$
 $$ \begin{align*}=\left|-nK^++\pi^*_+\left(\sigma^*_SY+\sum_{T\in{\cal T}} (na_T-b_T)T\right)\right|, \end{align*} $$
$$ \begin{align*}=\left|-nK^++\pi^*_+\left(\sigma^*_SY+\sum_{T\in{\cal T}} (na_T-b_T)T\right)\right|, \end{align*} $$
where
![]() $\sigma \colon V^+\to V$
is the composition of the morphisms
$\sigma \colon V^+\to V$
is the composition of the morphisms
![]() $\sigma _i$
,
$\sigma _i$
,
![]() $K^+=K_{V^+}$
,
$K^+=K_{V^+}$
,
![]() $b_T\geqslant 1$
and
$b_T\geqslant 1$
and
![]() $a_T\geqslant 1$
for all
$a_T\geqslant 1$
for all
![]() $T\in {\cal T}$
,
$T\in {\cal T}$
,
![]() $a_T=a(T,S)$
is the discrepancy of T with respect to S.
$a_T=a(T,S)$
is the discrepancy of T with respect to S.
Let
![]() $\varphi \colon \widetilde {V}\to V^+$
be the resolution of singularities of the composite map
$\varphi \colon \widetilde {V}\to V^+$
be the resolution of singularities of the composite map
![]() $\chi _+=\chi \circ \sigma \colon V^+\dashrightarrow V'$
,
$\chi _+=\chi \circ \sigma \colon V^+\dashrightarrow V'$
,
![]() ${\cal E}$
the set of prime
${\cal E}$
the set of prime
![]() $\varphi $
-exceptional divisors on
$\varphi $
-exceptional divisors on
![]() $\widetilde {V}$
and
$\widetilde {V}$
and
![]() $\psi =\chi \circ \sigma \circ \varphi \colon \widetilde {V}\to V'$
is a birational morphism.
$\psi =\chi \circ \sigma \circ \varphi \colon \widetilde {V}\to V'$
is a birational morphism.
Proposition 2.1. For a general divisor
![]() $D^+\in \Sigma ^+$
, the pair
$D^+\in \Sigma ^+$
, the pair
![]() $(V^+,\frac {1}{n}D^+)$
is canonical.
$(V^+,\frac {1}{n}D^+)$
is canonical.
Proof. Assume that this is not the case. Then there is an exceptional divisor
![]() $E\in {\cal E}$
, satisfying the Noether-Fano inequality
$E\in {\cal E}$
, satisfying the Noether-Fano inequality
(we write
![]() $D^+,\Sigma ^+$
instead of
$D^+,\Sigma ^+$
instead of
![]() $\varphi ^*D^+,\varphi ^*\Sigma ^+$
for simplicity). Set
$\varphi ^*D^+,\varphi ^*\Sigma ^+$
for simplicity). Set
![]() $B=\varphi (E)\subset V^+$
.
$B=\varphi (E)\subset V^+$
.
There are two options:
(1)
![]() $\pi _+(B)=S^+$
,
$\pi _+(B)=S^+$
,
(2)
![]() $\pi _+(B)$
is a proper irreducible closed subset
$\pi _+(B)$
is a proper irreducible closed subset
![]() $S^+$
.
$S^+$
.
If (1) is the case, then the fibre
![]() $F=F_s$
of general position intersects B. The restriction
$F=F_s$
of general position intersects B. The restriction
is a mobile linear system, and moreover, the pair
![]() $(F,\frac {1}{n}D^+_F)$
is not canonical for
$(F,\frac {1}{n}D^+_F)$
is not canonical for
![]() $D^+_F=D^+|_F$
. This contradicts the condition
$D^+_F=D^+|_F$
. This contradicts the condition
![]() $\mathop {\mathrm {mct}}(F)\geqslant 1$
.
$\mathop {\mathrm {mct}}(F)\geqslant 1$
.
Therefore, (2) is the case. Let
![]() $p\in B$
be a point of general position and
$p\in B$
be a point of general position and
![]() $F=\pi ^{-1}_+(\pi _+(p))$
, so that
$F=\pi ^{-1}_+(\pi _+(p))$
, so that
![]() $p\in F$
. Since
$p\in F$
. Since
![]() $F\not \subset \mathop {\mathrm {Bs}}\Sigma ^+$
, the restriction
$F\not \subset \mathop {\mathrm {Bs}}\Sigma ^+$
, the restriction
![]() $D^+_F=D^+|_F$
is well defined (although the linear system
$D^+_F=D^+|_F$
is well defined (although the linear system
![]() $\Sigma ^+_F$
may have fixed components). By inversion of adjunction, the pair
$\Sigma ^+_F$
may have fixed components). By inversion of adjunction, the pair
![]() $(F,\frac {1}{n}D^+_F)$
is not log-canonical. This contradicts the condition
$(F,\frac {1}{n}D^+_F)$
is not log-canonical. This contradicts the condition
![]() $\mathop {\mathrm {lct}}(F)\geqslant 1$
. Q.E.D. for the proposition.
$\mathop {\mathrm {lct}}(F)\geqslant 1$
. Q.E.D. for the proposition.
Denote by the symbol
![]() $\widetilde {\Sigma }$
the strict transform of the system
$\widetilde {\Sigma }$
the strict transform of the system
![]() $\Sigma ^+$
on
$\Sigma ^+$
on
![]() $\widetilde {V}$
. Obviously,
$\widetilde {V}$
. Obviously,
where
![]() $K'=K_{V'}$
; that is,
$K'=K_{V'}$
; that is,
![]() $\widetilde {\Sigma }$
is a complete linear system. We have another presentation for this linear system:
$\widetilde {\Sigma }$
is a complete linear system. We have another presentation for this linear system:
 $$ \begin{align*}\widetilde{\Sigma}=\left|\varphi^*D^+-\sum_{E\in{\cal E}}b_EE\right|= \end{align*} $$
$$ \begin{align*}\widetilde{\Sigma}=\left|\varphi^*D^+-\sum_{E\in{\cal E}}b_EE\right|= \end{align*} $$
 $$ \begin{align} =\left|-n\widetilde{K}+\varphi^*\pi^*_+\left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)+\sum_{E\in{\cal E}}(na_E-b_E)E\right|, \end{align} $$
$$ \begin{align} =\left|-n\widetilde{K}+\varphi^*\pi^*_+\left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)+\sum_{E\in{\cal E}}(na_E-b_E)E\right|, \end{align} $$
where
![]() $\widetilde {K}=K_{\widetilde {V}}$
,
$\widetilde {K}=K_{\widetilde {V}}$
,
![]() $D^+\in \Sigma ^+$
is a general divisor and
$D^+\in \Sigma ^+$
is a general divisor and
![]() $a_E=a(E,V^+)$
is the discrepancy.
$a_E=a(E,V^+)$
is the discrepancy.
2.3 The mobile system of curves
Take a family of irreducible curves
![]() ${\cal C'}$
on
${\cal C'}$
on
![]() $V'$
, contracted by the projection
$V'$
, contracted by the projection
![]() $\pi '$
, sweeping out a Zariski dense subset of the variety
$\pi '$
, sweeping out a Zariski dense subset of the variety
![]() $V'$
and not meeting the set where the birational map
$V'$
and not meeting the set where the birational map
![]() $\psi ^{-1}$
is not determined. Assume that for a general pair of points
$\psi ^{-1}$
is not determined. Assume that for a general pair of points
![]() $p,q$
in a fibre of general position of the projection
$p,q$
in a fibre of general position of the projection
![]() $\pi '$
, there is a curve
$\pi '$
, there is a curve
![]() $C'\in {\cal C'}$
containing the both points. In the rationally connected case, the curves of the family
$C'\in {\cal C'}$
containing the both points. In the rationally connected case, the curves of the family
![]() ${\cal C'}$
are rational (the existence of such family is shown in [Reference Kollár24, Chapter II]); in the case of a Mori fibre space, we do not require this. For a curve
${\cal C'}$
are rational (the existence of such family is shown in [Reference Kollár24, Chapter II]); in the case of a Mori fibre space, we do not require this. For a curve
![]() $C'\in {\cal C'}$
, set
$C'\in {\cal C'}$
, set
![]() $\widetilde {C}=\psi ^{-1}(C')$
(at every point of the curve
$\widetilde {C}=\psi ^{-1}(C')$
(at every point of the curve
![]() $C'$
, the map
$C'$
, the map
![]() $\psi ^{-1}$
is an isomorphism); thus, we get a family
$\psi ^{-1}$
is an isomorphism); thus, we get a family
![]() $\widetilde {{\cal C}}$
of irreducible curves on
$\widetilde {{\cal C}}$
of irreducible curves on
![]() $\widetilde {V}$
. Both in the rationally connected case and the case of a Mori fibre space, the inequality
$\widetilde {V}$
. Both in the rationally connected case and the case of a Mori fibre space, the inequality
holds, so that
![]() $(\widetilde {C}\cdot \widetilde {K})=(C'\cdot K')<0$
. Furthermore,.
$(\widetilde {C}\cdot \widetilde {K})=(C'\cdot K')<0$
. Furthermore,.
and
![]() $(\widetilde {C}\cdot \widetilde {D})=0$
if and only if
$(\widetilde {C}\cdot \widetilde {D})=0$
if and only if
![]() $m=0$
(since obviously
$m=0$
(since obviously
![]() $(C'\cdot (\pi ')^*Y')=0$
).
$(C'\cdot (\pi ')^*Y')=0$
).
Let
![]() ${\cal C}^+=\varphi _*\widetilde {{\cal C}}$
be the image of the family
${\cal C}^+=\varphi _*\widetilde {{\cal C}}$
be the image of the family
![]() $\widetilde {{\cal C}}$
on
$\widetilde {{\cal C}}$
on
![]() $V^+$
and
$V^+$
and
![]() ${\cal C} =\sigma _*{\cal C}^+$
its image on V.
${\cal C} =\sigma _*{\cal C}^+$
its image on V.
Proposition 2.2. The curves
![]() $C\in {\cal C}$
are not contracted by the projection
$C\in {\cal C}$
are not contracted by the projection
![]() $\pi $
.
$\pi $
.
Proof. Assume the converse:
![]() $\pi (C)$
is a point on S. By the construction of the family
$\pi (C)$
is a point on S. By the construction of the family
![]() ${\cal C}'$
this means that the map
${\cal C}'$
this means that the map
![]() $\chi ^{-1}$
is fibre-wise: there is a rational dominant map
$\chi ^{-1}$
is fibre-wise: there is a rational dominant map
![]() $\beta '\colon S'\dashrightarrow S$
, such that the diagram
$\beta '\colon S'\dashrightarrow S$
, such that the diagram
 $$ \begin{align*}\begin{array}{ccc} V & \stackrel{\phantom{xxx}\chi^{-1}}{\dashleftarrow} & V'\\ \downarrow & & \downarrow \\ S & \stackrel{\phantom{xx}\beta'}{\dashleftarrow} & S' \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} V & \stackrel{\phantom{xxx}\chi^{-1}}{\dashleftarrow} & V'\\ \downarrow & & \downarrow \\ S & \stackrel{\phantom{xx}\beta'}{\dashleftarrow} & S' \end{array} \end{align*} $$
is commutative, and moreover,
![]() $\dim S'> \dim S$
(otherwise,
$\dim S'> \dim S$
(otherwise,
![]() $\beta '$
is birational and then
$\beta '$
is birational and then
![]() $\chi $
is fibre-wise, contrary to our assumption). In that case, for a point
$\chi $
is fibre-wise, contrary to our assumption). In that case, for a point
![]() $s\in S$
of general position, the fibre
$s\in S$
of general position, the fibre
![]() $F_s=\pi ^{-1}(s)$
is birational to
$F_s=\pi ^{-1}(s)$
is birational to
![]() $(\pi ')^{-1}(\beta ')^{-1}(s)$
. Here,
$(\pi ')^{-1}(\beta ')^{-1}(s)$
. Here,
![]() $\dim (\beta ')^{-1}(s)\geqslant 1$
and either the fibre
$\dim (\beta ')^{-1}(s)\geqslant 1$
and either the fibre
![]() $(\pi ')^{-1}(s')$
for a point
$(\pi ')^{-1}(s')$
for a point
![]() $s'\in (\beta ')^{-1}(s)$
of general position is rationally connected or the anti-canonical class of the variety
$s'\in (\beta ')^{-1}(s)$
of general position is rationally connected or the anti-canonical class of the variety
![]() $(\pi ')^{-1}(\beta ')^{-1}(s)$
is
$(\pi ')^{-1}(\beta ')^{-1}(s)$
is
![]() $\pi '$
-ample, and we get a contradiction with the condition
$\pi '$
-ample, and we get a contradiction with the condition
![]() $\mathop {\mathrm {mct}} (F_s)\geqslant 1$
(the fibre
$\mathop {\mathrm {mct}} (F_s)\geqslant 1$
(the fibre
![]() $F_s$
is a birationally superrigid Fano variety). Q.E.D. for the proposition.
$F_s$
is a birationally superrigid Fano variety). Q.E.D. for the proposition.
For a general curve
![]() $C\in {\cal C}$
, set
$C\in {\cal C}$
, set
where
![]() $d_C\geqslant 1$
. Replacing, if necessary, the family
$d_C\geqslant 1$
. Replacing, if necessary, the family
![]() $\cal {C}'$
by some open subfamily, we may assume that the integer
$\cal {C}'$
by some open subfamily, we may assume that the integer
![]() $d_C$
does not depend on C. For the corresponding curve
$d_C$
does not depend on C. For the corresponding curve
![]() $C^+\in \cal {C}^+$
, we have
$C^+\in \cal {C}^+$
, we have
![]() $(\pi _+)_*C^+=d_C\overline {C}^+$
, where
$(\pi _+)_*C^+=d_C\overline {C}^+$
, where
![]() $\overline {C}^+$
is the strict transform of the curve
$\overline {C}^+$
is the strict transform of the curve
![]() $\overline {C}$
on
$\overline {C}$
on
![]() $S^+$
.
$S^+$
.
2.4 Proof of Theorem 2.1
Recall that we assume that
![]() $n>m$
. Using the two presentations (8) and (9) for the class of a divisor
$n>m$
. Using the two presentations (8) and (9) for the class of a divisor
![]() $\widetilde {D}\in \widetilde {\Sigma }$
, we get
$\widetilde {D}\in \widetilde {\Sigma }$
, we get
 $$ \begin{align*}d_C\left(\overline{C}^+\cdot\left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)\right)+\sum_{E\in{\cal E}}(na_E-b_E)(\widetilde{C}\cdot E)= (n-m)(\widetilde{C}\cdot\widetilde{K})<0, \end{align*} $$
$$ \begin{align*}d_C\left(\overline{C}^+\cdot\left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)\right)+\sum_{E\in{\cal E}}(na_E-b_E)(\widetilde{C}\cdot E)= (n-m)(\widetilde{C}\cdot\widetilde{K})<0, \end{align*} $$
whence, taking into account the inequalities
![]() $b_E\leqslant na_E$
for all
$b_E\leqslant na_E$
for all
![]() $E\in {\cal E}$
(Proposition 2.1), it follows that
$E\in {\cal E}$
(Proposition 2.1), it follows that
 $$ \begin{align*}\left(\overline{C}^+\cdot \left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)\right)<0. \end{align*} $$
$$ \begin{align*}\left(\overline{C}^+\cdot \left(\sigma^*_SY+\sum_{T\in{\cal T}}(na_T-b_T)T\right)\right)<0. \end{align*} $$
However, by the K-condition (the assumption (ii) in Theorem 0.2), the class Y is pseudo-effective, so that
and
![]() $(\overline {C}^+\cdot T)\geqslant 0$
for all
$(\overline {C}^+\cdot T)\geqslant 0$
for all
![]() $T\in {\cal T}$
, so that
$T\in {\cal T}$
, so that
![]() ${\cal T}\neq \emptyset $
, and for some
${\cal T}\neq \emptyset $
, and for some
![]() $T\in {\cal T}$
, such that
$T\in {\cal T}$
, such that
![]() $(\overline {C}^+\cdot T)>0$
, the inequality
$(\overline {C}^+\cdot T)>0$
, the inequality
![]() $b_T>na_T$
holds. Since
$b_T>na_T$
holds. Since
![]() $a_T\geqslant 1$
for all
$a_T\geqslant 1$
for all
![]() $T\in {\cal T}$
, we conclude that
$T\in {\cal T}$
, we conclude that
 $$ \begin{align*}\left(\overline{C}^+\cdot\left(\sigma^*_SY-\sum_{T\in{\cal T}} b_T T \right)\right)< -n\left(\overline{C}^+\cdot \sum_{T\in{\cal T}} a_T T \right)\leqslant -n. \end{align*} $$
$$ \begin{align*}\left(\overline{C}^+\cdot\left(\sigma^*_SY-\sum_{T\in{\cal T}} b_T T \right)\right)< -n\left(\overline{C}^+\cdot \sum_{T\in{\cal T}} a_T T \right)\leqslant -n. \end{align*} $$
For a general curve
![]() $\overline {C}^+$
, consider the algebraic cycle of the scheme-theoretic intersection
$\overline {C}^+$
, consider the algebraic cycle of the scheme-theoretic intersection
 $$ \begin{align*}(D^+\circ \pi_+^{-1}(\overline{C}^+))=\left(\left(\sigma^* D-\pi_+^*\left(\sum_{T\in{\cal T}}b_T T\right)\right)\circ\pi_+^{-1}(\overline{C}^+)\right). \end{align*} $$
$$ \begin{align*}(D^+\circ \pi_+^{-1}(\overline{C}^+))=\left(\left(\sigma^* D-\pi_+^*\left(\sum_{T\in{\cal T}}b_T T\right)\right)\circ\pi_+^{-1}(\overline{C}^+)\right). \end{align*} $$
The numerical class of that effective cycle is
 $$ \begin{align*}n(\sigma^*(-K_V)\cdot\pi^{-1}_+(\overline{C}^+))+\left(\overline{C}^+ \cdot\left(\sigma^*_S Y-\sum_{T\in{\cal T}}b_TT\right)\right)F \end{align*} $$
$$ \begin{align*}n(\sigma^*(-K_V)\cdot\pi^{-1}_+(\overline{C}^+))+\left(\overline{C}^+ \cdot\left(\sigma^*_S Y-\sum_{T\in{\cal T}}b_TT\right)\right)F \end{align*} $$
(where F is the class of a fibre of the projection
![]() $\pi _+$
) and the class of the effective cycle
$\pi _+$
) and the class of the effective cycle
![]() $\sigma _*(D^+\circ \pi ^{-1}_+(\overline {C}^+ ))$
in the numerical Chow group is
$\sigma _*(D^+\circ \pi ^{-1}_+(\overline {C}^+ ))$
in the numerical Chow group is
where
![]() $b<-n$
. This contradicts the condition (iii) of Theorem 0.2. The proof of Theorem 2.1 is complete. Therefore, in both cases (that of a rationally connected fibre space and of a Mori fibre space), the map
$b<-n$
. This contradicts the condition (iii) of Theorem 0.2. The proof of Theorem 2.1 is complete. Therefore, in both cases (that of a rationally connected fibre space and of a Mori fibre space), the map
![]() $\chi $
is fibre-wise. The first claim of Theorem 0.2 (in the rationally connected case) is shown. It remains to prove the birational rigidity.
$\chi $
is fibre-wise. The first claim of Theorem 0.2 (in the rationally connected case) is shown. It remains to prove the birational rigidity.
2.5 Proof of birational rigidity
Starting from this moment, we assume that
![]() $V'/S'$
is a Mori fibre space and the birational map
$V'/S'$
is a Mori fibre space and the birational map
![]() $\chi \colon V\dashrightarrow V'$
is fibre-wise; however, the corresponding map of the bases
$\chi \colon V\dashrightarrow V'$
is fibre-wise; however, the corresponding map of the bases
![]() $\beta \colon S\dashrightarrow S'$
is not birational:
$\beta \colon S\dashrightarrow S'$
is not birational:
![]() $\mathop {\mathrm {dim}}S>\mathop {\mathrm {dim}}S'$
and the fibres
$\mathop {\mathrm {dim}}S>\mathop {\mathrm {dim}}S'$
and the fibres
![]() $\beta ^{-1}(s')$
for
$\beta ^{-1}(s')$
for
![]() $s'\in S'$
are of positive dimension. We have to obtain a contradiction, showing that this case is impossible.
$s'\in S'$
are of positive dimension. We have to obtain a contradiction, showing that this case is impossible.
First of all, let us consider the fibre-wise modification of the fibre space
![]() $V/S$
(Subsection 2.2). Now we will need a composition of blow-ups
$V/S$
(Subsection 2.2). Now we will need a composition of blow-ups
![]() $\sigma _S\colon S^+\to S$
with non-singular centres such that as in Subsection 2.2, none of the fibres of the Fano-Mori fibre space
$\sigma _S\colon S^+\to S$
with non-singular centres such that as in Subsection 2.2, none of the fibres of the Fano-Mori fibre space
![]() $V^+/S^+$
are contained in the base set
$V^+/S^+$
are contained in the base set
![]() $\mathop {\mathrm {Bs}}\Sigma ^+$
, and, in addition,
$\mathop {\mathrm {Bs}}\Sigma ^+$
, and, in addition,
![]() $\sigma _S$
resolves the singularities of the rational dominant map
$\sigma _S$
resolves the singularities of the rational dominant map
![]() $\beta \colon S\dashrightarrow S'$
; that is,
$\beta \colon S\dashrightarrow S'$
; that is,
is a morphism. (So that the inclusion
![]() $Z_i=\pi ^{-1}_i(Z_{S,i})\subset \mathop {\mathrm {Bs}}\Sigma ^i$
– see Subsection 2.2 – no longer takes place for all
$Z_i=\pi ^{-1}_i(Z_{S,i})\subset \mathop {\mathrm {Bs}}\Sigma ^i$
– see Subsection 2.2 – no longer takes place for all
![]() $i=0,\dots ,N-1$
.)
$i=0,\dots ,N-1$
.)
The fibre
![]() $\beta ^{-1}_+(s')$
over a point
$\beta ^{-1}_+(s')$
over a point
![]() $s'\in S'$
of general position is an irreducible non-singular subvariety of positive dimension. Set
$s'\in S'$
of general position is an irreducible non-singular subvariety of positive dimension. Set
![]() $G(s')=(\pi ')^{-1}(s')$
and let
$G(s')=(\pi ')^{-1}(s')$
and let
![]() $G^+(s')$
be the strict transform of
$G^+(s')$
be the strict transform of
![]() $G(s')$
on
$G(s')$
on
![]() $V^+$
. Obviously,
$V^+$
. Obviously,
is a union of fibres of the projection
![]() $\pi _+$
over the points of the variety
$\pi _+$
over the points of the variety
![]() $\beta ^{-1}_+(s')$
.
$\beta ^{-1}_+(s')$
.
Since
![]() $\pi '\colon V'\to S'$
is a Mori fibre space, we have the equality
$\pi '\colon V'\to S'$
is a Mori fibre space, we have the equality
![]() $\rho (V')=\rho (S')+1$
. Let
$\rho (V')=\rho (S')+1$
. Let
![]() ${\cal E}'$
be the set of all
${\cal E}'$
be the set of all
![]() $\psi $
-exceptional divisors
$\psi $
-exceptional divisors
![]() $E'\in {\cal E}'$
, satisfying the equality
$E'\in {\cal E}'$
, satisfying the equality
![]() $\pi '(\psi (E'))=S'$
. Furthermore, let
$\pi '(\psi (E'))=S'$
. Furthermore, let
![]() ${\cal Z}\subset \mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
be the subspace, generated by the subspace
${\cal Z}\subset \mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
be the subspace, generated by the subspace
![]() $\psi ^*(\pi ')^*\mathop {\mathrm {Pic}}S'\otimes {\mathbb Q}$
and the classes of all
$\psi ^*(\pi ')^*\mathop {\mathrm {Pic}}S'\otimes {\mathbb Q}$
and the classes of all
![]() $\psi $
-exceptional divisors on
$\psi $
-exceptional divisors on
![]() $\widetilde {V}$
, the images of which on
$\widetilde {V}$
, the images of which on
![]() $V'$
do not cover
$V'$
do not cover
![]() $S'$
. Then the equality
$S'$
. Then the equality
 $$ \begin{align*}\mathop{\mathrm{Pic}}\widetilde{V}\otimes{\mathbb Q}={}\mathbb Q\widetilde{K}\oplus\left(\bigoplus_{E'\in{\cal E}'}{\mathbb Q}E'\oplus {\cal Z}\right)\end{align*} $$
$$ \begin{align*}\mathop{\mathrm{Pic}}\widetilde{V}\otimes{\mathbb Q}={}\mathbb Q\widetilde{K}\oplus\left(\bigoplus_{E'\in{\cal E}'}{\mathbb Q}E'\oplus {\cal Z}\right)\end{align*} $$
holds; in particular, the subspace in brackets is a hyperplane in
![]() $\mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
. Writing down the class
$\mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
. Writing down the class
![]() $\widetilde {K}$
with respect to the morphisms
$\widetilde {K}$
with respect to the morphisms
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, we get the equality
$\psi $
, we get the equality
where
![]() $Z_1\in {\cal Z}$
is some effective class,
$Z_1\in {\cal Z}$
is some effective class,
![]() $a^+_E=a(E,V^+)$
for
$a^+_E=a(E,V^+)$
for
![]() $\varphi $
-exceptional divisors
$\varphi $
-exceptional divisors
![]() $E\in {\cal E}$
and
$E\in {\cal E}$
and
![]() $a'(E')=a(E',V')$
for
$a'(E')=a(E',V')$
for
![]() $\psi $
-exceptional divisors
$\psi $
-exceptional divisors
![]() $E'\in {\cal E}'$
, covering
$E'\in {\cal E}'$
, covering
![]() $S'$
. Here, all
$S'$
. Here, all
![]() $a^+_E\geqslant 1$
and
$a^+_E\geqslant 1$
and
![]() $a'(E')>0$
. Using the
$a'(E')>0$
. Using the
![]() $\psi $
-presentation (8) and the
$\psi $
-presentation (8) and the
![]() $\varphi $
-presentation (9) of the divisorial class
$\varphi $
-presentation (9) of the divisorial class
![]() $\widetilde {D}$
and expressing
$\widetilde {D}$
and expressing
![]() $K'$
from the formula (10), we get the following equality in
$K'$
from the formula (10), we get the following equality in
![]() $\mathbb {\mathrm { Pic}}\widetilde {V}\otimes {\mathbb Q}$
:
$\mathbb {\mathrm { Pic}}\widetilde {V}\otimes {\mathbb Q}$
:
where
![]() $Y_+=\sigma ^*_SY+\sum _{T\in {\cal T}}(na_T-b_T)T$
and
$Y_+=\sigma ^*_SY+\sum _{T\in {\cal T}}(na_T-b_T)T$
and
![]() $Z_2=mZ_1+\psi ^*(\pi ')^*Y'\in {\cal Z}$
is an effective class. Applying to both sides of (11)
$Z_2=mZ_1+\psi ^*(\pi ')^*Y'\in {\cal Z}$
is an effective class. Applying to both sides of (11)
![]() $\varphi _*$
and restricting onto a fibre of general position of the projection
$\varphi _*$
and restricting onto a fibre of general position of the projection
![]() $\pi _+$
, we get that
$\pi _+$
, we get that
is an effective class. Since
![]() $m\geqslant n$
and the fibre
$m\geqslant n$
and the fibre
![]() $\pi _+^{-1}(s_+)$
is a Fano variety, we conclude that
$\pi _+^{-1}(s_+)$
is a Fano variety, we conclude that
![]() $m=n$
and (11) turns into
$m=n$
and (11) turns into
By Proposition 2.1, we have
![]() $b_E\leqslant na^+_E$
for all
$b_E\leqslant na^+_E$
for all
![]() $E\in {\cal E}$
. Again, we apply
$E\in {\cal E}$
. Again, we apply
![]() $\varphi _*$
and get that the class
$\varphi _*$
and get that the class
![]() $Y_+$
is effective on
$Y_+$
is effective on
![]() $S^+$
.
$S^+$
.
Now let us consider the defined above fibre
![]() $G=G(s')$
of general position of the morphism
$G=G(s')$
of general position of the morphism
![]() $\pi '$
and its strict transforms
$\pi '$
and its strict transforms
![]() $\widetilde {G}$
on
$\widetilde {G}$
on
![]() $\widetilde {V}$
and
$\widetilde {V}$
and
![]() $G^+$
on
$G^+$
on
![]() $V^+$
(the symbol
$V^+$
(the symbol
![]() $s'$
for simplicity of notations is omitted). Obviously, for every
$s'$
for simplicity of notations is omitted). Obviously, for every
![]() $Z\in {\cal Z}$
, we have
$Z\in {\cal Z}$
, we have
![]() $Z|_{\widetilde {G}}=0$
. Furthermore, for any linear combination with non-negative coefficients,
$Z|_{\widetilde {G}}=0$
. Furthermore, for any linear combination with non-negative coefficients,
 $$ \begin{align*}\left.\left(\sum_{E'\in{\cal E'}}b'_{E'}E'\right)\right|_{\widetilde{G}} \end{align*} $$
$$ \begin{align*}\left.\left(\sum_{E'\in{\cal E'}}b'_{E'}E'\right)\right|_{\widetilde{G}} \end{align*} $$
is a fixed divisor on
![]() $\widetilde {G}$
. Now let
$\widetilde {G}$
. Now let
![]() $\Delta $
be a very ample divisor on
$\Delta $
be a very ample divisor on
![]() $S^+$
. Then the restriction
$S^+$
. Then the restriction
![]() $\varphi ^*\pi ^*_+\Delta |_{\widetilde {G}}$
is mobile (recall that
$\varphi ^*\pi ^*_+\Delta |_{\widetilde {G}}$
is mobile (recall that
![]() $\beta ^{-1}_+(s')$
is a variety of positive dimension, so that
$\beta ^{-1}_+(s')$
is a variety of positive dimension, so that
![]() $\Delta |_{\beta ^{-1}_+(s')}$
is a mobile class). Therefore,
$\Delta |_{\beta ^{-1}_+(s')}$
is a mobile class). Therefore,
whence we conclude that
 $$ \begin{align*}\mathop{\mathrm{Pic}}\widetilde{V}\otimes{\mathbb Q}={\mathbb Q}[\varphi^*\pi^*_+\Delta]\oplus\left(\bigoplus_{E'\in{\cal E'}}{\mathbb Q}E'\oplus{\cal Z}\right). \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{Pic}}\widetilde{V}\otimes{\mathbb Q}={\mathbb Q}[\varphi^*\pi^*_+\Delta]\oplus\left(\bigoplus_{E'\in{\cal E'}}{\mathbb Q}E'\oplus{\cal Z}\right). \end{align*} $$
However, this cannot be the case. Let
![]() $F^+\subset G^+$
be a fibre of general position of the morphism
$F^+\subset G^+$
be a fibre of general position of the morphism
![]() $\pi _+$
and
$\pi _+$
and
![]() $\widetilde {F}\subset \widetilde {G}$
its strict transform on
$\widetilde {F}\subset \widetilde {G}$
its strict transform on
![]() $\widetilde {V}$
. Restricting (12) onto
$\widetilde {V}$
. Restricting (12) onto
![]() $\widetilde {F}$
, we obtain the equality
$\widetilde {F}$
, we obtain the equality
where on the right-hand side, it is a linear combination of all divisors
![]() $E'|_{\widetilde {F}}$
,
$E'|_{\widetilde {F}}$
,
![]() $E'\in {\cal E'}$
, with positive coefficients (it is here that we use the assumption that the singularities of the variety
$E'\in {\cal E'}$
, with positive coefficients (it is here that we use the assumption that the singularities of the variety
![]() $V'$
are terminal; see Subsection 0.2), and on the left-hand side, it is a linear combination of
$V'$
are terminal; see Subsection 0.2), and on the left-hand side, it is a linear combination of
![]() $\varphi $
-exceptional divisors
$\varphi $
-exceptional divisors
![]() $E|_{\widetilde {F}}$
,
$E|_{\widetilde {F}}$
,
![]() $E\in {\cal E}$
, with non-negative coefficients. Since by construction
$E\in {\cal E}$
, with non-negative coefficients. Since by construction
![]() $\pi ^*_+\Delta |_{F^+}=0$
, we have
$\pi ^*_+\Delta |_{F^+}=0$
, we have
![]() $\varphi ^*\pi ^*_+\Delta |_{\widetilde {F}}=0$
, whence it follows that the restriction of every divisorial class in
$\varphi ^*\pi ^*_+\Delta |_{\widetilde {F}}=0$
, whence it follows that the restriction of every divisorial class in
![]() $\mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
onto
$\mathop {\mathrm {Pic}}\widetilde {V}\otimes {\mathbb Q}$
onto
![]() $\widetilde {F}$
is fixed (is a linear combination of
$\widetilde {F}$
is fixed (is a linear combination of
![]() $\varphi $
-exceptional divisors
$\varphi $
-exceptional divisors
![]() $E|_F,E\in {\cal E}$
), which is impossible. This contradiction completes the proof of Theorem 0.2.
$E|_F,E\in {\cal E}$
), which is impossible. This contradiction completes the proof of Theorem 0.2.
3 Hyperplane sections
This section is an immediate follow up of §1: we develop the technique of working triples and consider its first applications.
3.1 The working triple
 $(F,D_F,o)$
$(F,D_F,o)$
Let us prove Proposition 1.6. Proposition 1.2, shown in Subsection 1.5, implies the condition (MC3). Theorem 1.1 gives the condition (MC1) for
![]() $c_F=4k+2\varepsilon (k)$
(the inequality
$c_F=4k+2\varepsilon (k)$
(the inequality
![]() $c_F\geqslant l+4$
is satisfied in the obvious way, since
$c_F\geqslant l+4$
is satisfied in the obvious way, since
![]() $l\leqslant k$
). Finally, the condition (MQ1) gives precisely (MC2). Therefore,
$l\leqslant k$
). Finally, the condition (MQ1) gives precisely (MC2). Therefore,
![]() $[F,o]$
is indeed a marked complete intersection of level
$[F,o]$
is indeed a marked complete intersection of level
![]() $(l,c_F)$
.
$(l,c_F)$
.
Consider a general subspace
![]() $P^{\sharp }\ni o$
of dimension
$P^{\sharp }\ni o$
of dimension
![]() $k+c_F$
in
$k+c_F$
in
![]() ${\mathbb P}^{M+k}$
. The pair
${\mathbb P}^{M+k}$
. The pair
 $$ \begin{align*}\left(F\cap P^{\sharp},\frac{1}{n(D_F)}D_F|_{F\cap P^{\sharp}}\right) \end{align*} $$
$$ \begin{align*}\left(F\cap P^{\sharp},\frac{1}{n(D_F)}D_F|_{F\cap P^{\sharp}}\right) \end{align*} $$
is not canonical. By (MC1), the singularities of the variety
![]() ${F\cap P^{\sharp }}$
are zero-dimensional, and moreover,
${F\cap P^{\sharp }}$
are zero-dimensional, and moreover,
![]() $o\in \mathop {\mathrm {Sing}}{F\cap P^{\sharp }}$
and
$o\in \mathop {\mathrm {Sing}}{F\cap P^{\sharp }}$
and
 $$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P^{\sharp},\frac{1}{n(D_F)}D_F|_{F\cap P^{\sharp}}\right)\subset\mathop{\mathrm{Sing}} (F\cap P^{\sharp}), \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{CS}}\left(F\cap P^{\sharp},\frac{1}{n(D_F)}D_F|_{F\cap P^{\sharp}}\right)\subset\mathop{\mathrm{Sing}} (F\cap P^{\sharp}), \end{align*} $$
and the point o is an (isolated) centre of some non-canonical singularity of that pair. For a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+c_F-1$
, take a general hyperplane in
$k+c_F-1$
, take a general hyperplane in
![]() $P^{\sharp }$
, containing the point o. By inversion of adjunction, we have the equalities
$P^{\sharp }$
, containing the point o. By inversion of adjunction, we have the equalities
 $$ \begin{align*}\{o\}=\mathop{\mathrm{LCS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right)= \mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right), \end{align*} $$
$$ \begin{align*}\{o\}=\mathop{\mathrm{LCS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right)= \mathop{\mathrm{CS}}\left(F\cap P,\frac{1}{n(D_F)}D_F|_{F\cap P}\right), \end{align*} $$
and this is precisely (7). Q.E.D. for Proposition 1.6.
As we explained in Subsection 1.7, from now, our work is constructing a certain special sequence of working triples. This sequence starts with the working triple
![]() $(F,D_F,o)$
. In order to construct the sequence, we will need certain facts about working triples.
$(F,D_F,o)$
. In order to construct the sequence, we will need certain facts about working triples.
3.2 Multiplicity at the marked point
Let us prove Proposition 1.5. We use the notations of Subsection 1.7 and work with a working triple
![]() $(X,D,o)$
, where
$(X,D,o)$
, where
![]() $[X,o]$
is a marked complete intersection. Assume that
$[X,o]$
is a marked complete intersection. Assume that
![]() $\nu (D)\leqslant 2n(D)$
(otherwise, there is nothing to prove).
$\nu (D)\leqslant 2n(D)$
(otherwise, there is nothing to prove).
Since for a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $m\in I_X$
, the inequality
$m\in I_X$
, the inequality
![]() $a(E_{X\cap P})\geqslant 2$
holds (see Remark 1.2), the pair
$a(E_{X\cap P})\geqslant 2$
holds (see Remark 1.2), the pair
 $$ \begin{align*}\left((X\cap P)^+,\frac{1}{n(D)}D^+_P\right) \end{align*} $$
$$ \begin{align*}\left((X\cap P)^+,\frac{1}{n(D)}D^+_P\right) \end{align*} $$
is not log-canonical, and moreover,
 $$ \begin{align*}\mathop{\mathrm{LCS}}\left((X\cap P)^+,\frac{1}{n(D)}D^+_P\right)\subset E_{X\cap P}. \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{LCS}}\left((X\cap P)^+,\frac{1}{n(D)}D^+_P\right)\subset E_{X\cap P}. \end{align*} $$
Let
![]() $B(P)\subset E_{X\cap P}$
be the centre of some non-log-canonical singularity of that pair. Then the inequality
$B(P)\subset E_{X\cap P}$
be the centre of some non-log-canonical singularity of that pair. Then the inequality
holds, and the more so,
Considering a general subspace
![]() $P^*\ni o$
of the minimal admissible dimension
$P^*\ni o$
of the minimal admissible dimension
![]() $k+l_X+3$
in
$k+l_X+3$
in
![]() $I_X$
as a general subspace of codimension
$I_X$
as a general subspace of codimension
![]() $\geqslant l_X$
in a general subspace
$\geqslant l_X$
in a general subspace
![]() $P\ni o$
of the maximal admissible dimension
$P\ni o$
of the maximal admissible dimension
![]() $k+c_X-1$
in
$k+c_X-1$
in
![]() $I_X$
(recall that by assumption
$I_X$
(recall that by assumption
![]() $c_X\geqslant 2l_X+4$
), we see that the centre
$c_X\geqslant 2l_X+4$
), we see that the centre
![]() $B(P)$
of some non-log-canonical singularity is of dimension
$B(P)$
of some non-log-canonical singularity is of dimension
![]() $\geqslant l_X$
. However,
$\geqslant l_X$
. However,
![]() $E_{X\cap P}$
is a non-singular complete intersection of
$E_{X\cap P}$
is a non-singular complete intersection of
![]() $l_X$
quadrics in the projective space of dimension
$l_X$
quadrics in the projective space of dimension
![]() $l_X+c_X-2$
, and the divisor
$l_X+c_X-2$
, and the divisor
![]() $D^+_P|_{E_{X\cap P}}$
is cut out on
$D^+_P|_{E_{X\cap P}}$
is cut out on
![]() $E_{X\cap P}$
by a hypersurface of degree
$E_{X\cap P}$
by a hypersurface of degree
![]() $\nu (D)$
in that projective space. Therefore, (for example, by [Reference Pukhlikov17, Proposition 3.6]), the inequality
$\nu (D)$
in that projective space. Therefore, (for example, by [Reference Pukhlikov17, Proposition 3.6]), the inequality
holds. Therefore,
![]() $\nu (D)>n(D)$
. Q.E.D. for Proposition 1.5.
$\nu (D)>n(D)$
. Q.E.D. for Proposition 1.5.
3.3 Transversal hyperplane sections
We still work with an arbitrary working triple
![]() $(X,D,o)$
, where
$(X,D,o)$
, where
![]() $[X,o]$
is a marked complete intersection of level
$[X,o]$
is a marked complete intersection of level
![]() $(l_X, c_X)$
.
$(l_X, c_X)$
.
Proposition 3.1. Let
![]() $R\ni o$
be the section of the variety X by a hyperplane
$R\ni o$
be the section of the variety X by a hyperplane
![]() ${\mathbb P}(R)\subset {\mathbb P}(X)$
, which is not tangent to X at the point o. Then
${\mathbb P}(R)\subset {\mathbb P}(X)$
, which is not tangent to X at the point o. Then
![]() $D\neq bR$
for
$D\neq bR$
for
![]() $b\geqslant 1$
. Moreover, if D contains R as a component – that is,
$b\geqslant 1$
. Moreover, if D contains R as a component – that is,
where
![]() $b\geqslant 1$
– then
$b\geqslant 1$
– then
![]() $(X,D^*,o)$
is a working triple.
$(X,D^*,o)$
is a working triple.
Proof. If
![]() $c_X\geqslant 2l_X+4$
, then the first claim (that D is not a multiple of R) follows immediately from Proposition 1.5: indeed, the hyperplane
$c_X\geqslant 2l_X+4$
, then the first claim (that D is not a multiple of R) follows immediately from Proposition 1.5: indeed, the hyperplane
![]() ${\mathbb P}(R)$
is not tangent to X at the point o; that is, for the strict transform
${\mathbb P}(R)$
is not tangent to X at the point o; that is, for the strict transform
![]() $R^+$
on the blow-up of that point, we have
$R^+$
on the blow-up of that point, we have
so that the equality
![]() $D=bR$
implies that
$D=bR$
implies that
![]() $n(D)=b=\nu (D)$
, which contradicts Proposition 1.5. However, we will show now that the additional assumptions for the parameters
$n(D)=b=\nu (D)$
, which contradicts Proposition 1.5. However, we will show now that the additional assumptions for the parameters
![]() $l_X$
and
$l_X$
and
![]() $c_X$
are not needed.
$c_X$
are not needed.
By Remark 1.4, the condition (MC1) for X implies the inequality
Since the hyperplane
![]() ${\mathbb P}(R)$
is not tangent to X at the point o, this point is a multi-quadratic singularity of the variety R of type
${\mathbb P}(R)$
is not tangent to X at the point o, this point is a multi-quadratic singularity of the variety R of type
![]() $2^{l_X}$
, the rank of which (by Remark 1.4 and the condition (MC2)) satisfies the inequality
$2^{l_X}$
, the rank of which (by Remark 1.4 and the condition (MC2)) satisfies the inequality
Consider a general linear subspace
![]() $P\ni o$
in
$P\ni o$
in
![]() ${\mathbb P}(X)$
of dimension
${\mathbb P}(X)$
of dimension
![]() $k+c_X-2$
. That dimension, generally speaking, does not belong to
$k+c_X-2$
. That dimension, generally speaking, does not belong to
![]() $I_X$
, and only the inequality
$I_X$
, and only the inequality
holds. The variety
![]() $X\cap P$
has a unique singularity, the point o, and its strict transform
$X\cap P$
has a unique singularity, the point o, and its strict transform
![]() $(X\cap P)^+$
and the exceptional divisor
$(X\cap P)^+$
and the exceptional divisor
![]() $E_{X\cap P}$
are non-singular.
$E_{X\cap P}$
are non-singular.
The intersection
![]() $P\cap {\mathbb P}(R)$
is a general linear subspace of dimension
$P\cap {\mathbb P}(R)$
is a general linear subspace of dimension
![]() $k+c_X-3$
in
$k+c_X-3$
in
![]() ${\mathbb P}(R)$
, containing the point o. For that reason,
${\mathbb P}(R)$
, containing the point o. For that reason,
![]() $R\cap P$
has a unique singularity, the point o, and moreover, the exceptional divisor
$R\cap P$
has a unique singularity, the point o, and moreover, the exceptional divisor
is non-singular, and the map
![]() $(R\cap P)^+\to R\cap P$
is the blow-up of the point o on
$(R\cap P)^+\to R\cap P$
is the blow-up of the point o on
![]() $R\cap P$
, which resolves the singularities of that variety. From here, taking into account that
$R\cap P$
, which resolves the singularities of that variety. From here, taking into account that
it follows that the pair
![]() $(X\cap P,R\cap P)$
is canonical. By inversion of adjunction, we get that for every
$(X\cap P,R\cap P)$
is canonical. By inversion of adjunction, we get that for every
![]() $m\in I_X$
and a general subspace
$m\in I_X$
and a general subspace
![]() $P^{\sharp }\ni o$
of dimension m, the pair
$P^{\sharp }\ni o$
of dimension m, the pair
![]() $(X\cap P^{\sharp }, R\cap P^{\sharp })$
is canonical. Therefore,
$(X\cap P^{\sharp }, R\cap P^{\sharp })$
is canonical. Therefore,
![]() $D\neq bR$
,
$D\neq bR$
,
![]() $b\geqslant 1$
, and the first claim of the proposition is shown.
$b\geqslant 1$
, and the first claim of the proposition is shown.
Assume now that
![]() $D=D^*+bR$
, where
$D=D^*+bR$
, where
![]() $b\geqslant 1$
. Then for a general subspace
$b\geqslant 1$
. Then for a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+c_X-1$
in
$k+c_X-1$
in
![]() ${\mathbb P}(X)$
, the pair
${\mathbb P}(X)$
, the pair
![]() $(X\cap P, \frac {1}{n(D)}D_P)$
is not log canonical at the point o. As we saw above, the pair
$(X\cap P, \frac {1}{n(D)}D_P)$
is not log canonical at the point o. As we saw above, the pair
![]() $(X\cap P, R_P)$
is log-canonical (and even canonical). The condition of being log-canonical is linear, so we conclude that the pair
$(X\cap P, R_P)$
is log-canonical (and even canonical). The condition of being log-canonical is linear, so we conclude that the pair
 $$ \begin{align*}\left(X\cap P, \frac{1}{n(D^*)} D^*|_{X\cap P}\right) \end{align*} $$
$$ \begin{align*}\left(X\cap P, \frac{1}{n(D^*)} D^*|_{X\cap P}\right) \end{align*} $$
is not log-canonical at the point o. Therefore,
![]() $(X,D^*,o)$
is a working triple. Q.E.D. for the proposition.
$(X,D^*,o)$
is a working triple. Q.E.D. for the proposition.
Theorem 3.1 (on the transversal hyperplane section).
Let
![]() $[X,o]$
be a marked complete intersection of level
$[X,o]$
be a marked complete intersection of level
![]() $(l_X=k,c_X)$
, where
$(l_X=k,c_X)$
, where
![]() $c_X\geqslant k+6$
, and
$c_X\geqslant k+6$
, and
![]() $(X,D,o)$
a working triple. Let
$(X,D,o)$
a working triple. Let
![]() $R\ni o$
be a hyperplane section, which is not a component of the divisor D. Assume that the inequality
$R\ni o$
be a hyperplane section, which is not a component of the divisor D. Assume that the inequality
![]() $\mathop {\mathrm {ct}}(R\backslash \mathop {\mathrm {Sing}}R)\geqslant 1$
holds. Then
$\mathop {\mathrm {ct}}(R\backslash \mathop {\mathrm {Sing}}R)\geqslant 1$
holds. Then
![]() $(R,(D\circ R),o)$
is a working triple on the marked complete intersection
$(R,(D\circ R),o)$
is a working triple on the marked complete intersection
![]() $[R,o]$
of level
$[R,o]$
of level
![]() $(l_R=k,c_R)$
, where
$(l_R=k,c_R)$
, where
![]() $c_R=c_X-2$
.
$c_R=c_X-2$
.
Proof. First of all, let us check that
![]() $[R,o]$
is a marked complete intersection of level
$[R,o]$
is a marked complete intersection of level
![]() $(k,c_R)$
. The inequality
$(k,c_R)$
. The inequality
![]() $c_R\geqslant k+4$
holds by assumption. Furthermore,
$c_R\geqslant k+4$
holds by assumption. Furthermore,
so that the condition (MC1) is satisfied. Furthermore, the point
![]() $o\in R$
is a multi-quadratic singularity, the rank of which satisfies the inequality
$o\in R$
is a multi-quadratic singularity, the rank of which satisfies the inequality
so that the condition (MC2) holds. The condition (MC3) holds by assumption. The bound for the codimension of the singular set
![]() $\mathop {\mathrm {Sing}}R$
guarantees that the complete intersection
$\mathop {\mathrm {Sing}}R$
guarantees that the complete intersection
![]() $R\subset {\mathbb P}(R)$
is irreducible, reduced and factorial. Therefore,
$R\subset {\mathbb P}(R)$
is irreducible, reduced and factorial. Therefore,
![]() $[R,o]$
is a marked complete intersection of level
$[R,o]$
is a marked complete intersection of level
![]() $(k,c_R)$
. Set
$(k,c_R)$
. Set
Obviously,
![]() $(D\circ R)\sim n(D\circ R)H_R=n(D)H_R$
, where
$(D\circ R)\sim n(D\circ R)H_R=n(D)H_R$
, where
![]() $H_R$
is the class of a hyperplane section of R. It remains to check that for a general subspace
$H_R$
is the class of a hyperplane section of R. It remains to check that for a general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+c_R-1$
in
$k+c_R-1$
in
![]() ${\mathbb P}(R)$
, the pair
${\mathbb P}(R)$
, the pair
 $$ \begin{align} \left(R\cap P, \frac{1}{n(D\circ R)}(D\circ R)|_{R\cap P}\right) \end{align} $$
$$ \begin{align} \left(R\cap P, \frac{1}{n(D\circ R)}(D\circ R)|_{R\cap P}\right) \end{align} $$
is not log-canonical at the point o. In order to do this, we present P as the intersection
where
![]() $P^{\sharp }\ni o$
is a general subspace of dimension
$P^{\sharp }\ni o$
is a general subspace of dimension
in
![]() ${\mathbb P}(X)$
. As
${\mathbb P}(X)$
. As
![]() $k+c_R\in I_X$
, the point o is the only singularity of the variety
$k+c_R\in I_X$
, the point o is the only singularity of the variety
![]() $X\cap P^{\sharp }$
(and the only singularity of the variety
$X\cap P^{\sharp }$
(and the only singularity of the variety
![]() $R\cap P$
), and
$R\cap P$
), and
 $$ \begin{align*}\{o\}=\mathop{\mathrm{LCS}}\left(X\cap P^{\sharp},\frac{1}{n(D)}D|_{X\cap P^{\sharp}}\right). \end{align*} $$
$$ \begin{align*}\{o\}=\mathop{\mathrm{LCS}}\left(X\cap P^{\sharp},\frac{1}{n(D)}D|_{X\cap P^{\sharp}}\right). \end{align*} $$
The variety
![]() $R\cap P$
is the section of the variety
$R\cap P$
is the section of the variety
![]() $X\cap P^{\sharp }$
by the hyperplane
$X\cap P^{\sharp }$
by the hyperplane
![]() $P= P^{\sharp }\cap {\mathbb P}(R)$
, containing the point o, so that by inversion of adjunction the pair (14) is not log-canonical. At the same time, it is canonical outside the point o since the subspace
$P= P^{\sharp }\cap {\mathbb P}(R)$
, containing the point o, so that by inversion of adjunction the pair (14) is not log-canonical. At the same time, it is canonical outside the point o since the subspace
![]() $P\subset {\mathbb P}(R)$
is generic, the non-singular part
$P\subset {\mathbb P}(R)$
is generic, the non-singular part
![]() $R\backslash \mathop {\mathrm {Sing}}R$
is divisorially canonical and the equality
$R\backslash \mathop {\mathrm {Sing}}R$
is divisorially canonical and the equality
![]() $\{o\}=\mathop {\mathrm {Sing}}(R\cap P)$
holds. Therefore, the pair (14) is not log-canonical precisely at the point o, which completes the proof of Theorem 3.1.
$\{o\}=\mathop {\mathrm {Sing}}(R\cap P)$
holds. Therefore, the pair (14) is not log-canonical precisely at the point o, which completes the proof of Theorem 3.1.
3.4 Tangent hyperplane sections
Now let us consider a marked complete intersection
![]() $[X,o]$
of level
$[X,o]$
of level
![]() $(l_X,c_X)$
, where
$(l_X,c_X)$
, where
![]() $l_X\leqslant k-1$
. Let R be the section of the variety X by a hyperplane
$l_X\leqslant k-1$
. Let R be the section of the variety X by a hyperplane
![]() ${\mathbb P}(R)\subset {\mathbb P}(X)$
, which is tangent to X at the point o. By the symbol
${\mathbb P}(R)\subset {\mathbb P}(X)$
, which is tangent to X at the point o. By the symbol
![]() ${\mathbb P}(R)^+$
, denote the strict transform of the hyperplane
${\mathbb P}(R)^+$
, denote the strict transform of the hyperplane
![]() ${\mathbb P} (R)$
on
${\mathbb P} (R)$
on
![]() ${\mathbb P}(X)^+$
and set
${\mathbb P}(X)^+$
and set
Obviously,
![]() ${\mathbb E}_R\cong {\mathbb P}^{N(X)-2}$
is the exceptional divisor of the blow-up of the point o on the hyperplane
${\mathbb E}_R\cong {\mathbb P}^{N(X)-2}$
is the exceptional divisor of the blow-up of the point o on the hyperplane
![]() ${\mathbb P}(R)$
. Set also
${\mathbb P}(R)$
. Set also
![]() $E_R=R^+\cap {\mathbb E}_X$
. Obviously,
$E_R=R^+\cap {\mathbb E}_X$
. Obviously,
![]() $E_R\subset {\mathbb E}_R$
, and
$E_R\subset {\mathbb E}_R$
, and
Proposition 3.2. Assume that
![]() $c_X\geqslant l_X+5$
and the point
$c_X\geqslant l_X+5$
and the point
![]() $o\in R$
is a multi-quadratic singularity of type
$o\in R$
is a multi-quadratic singularity of type
![]() $2^{l_X+1}$
, and moreover, the inequality
$2^{l_X+1}$
, and moreover, the inequality
holds. Then
![]() $D\neq bR$
for
$D\neq bR$
for
![]() $b\geqslant 1$
. Moreover, if the divisor D contains R as a component – that is,
$b\geqslant 1$
. Moreover, if the divisor D contains R as a component – that is,
where
![]() $b\geqslant 1$
– then
$b\geqslant 1$
– then
![]() $(X,D^*,o)$
is a working triple.
$(X,D^*,o)$
is a working triple.
Proof is completely similar to the proof of Proposition 3.1, but we give it in full details because there are some small points where the two arguments are different. The inequality (13) holds in this case again. Let us use the additional assumption about the singularity
![]() $o\in R$
. Consider a general linear subspace
$o\in R$
. Consider a general linear subspace
![]() $P\ni o$
in
$P\ni o$
in
![]() ${\mathbb P}(X)$
of dimension
${\mathbb P}(X)$
of dimension
![]() $k+l_X+3$
(it is the minimal admissible dimension). We get the equality
$k+l_X+3$
(it is the minimal admissible dimension). We get the equality
![]() $a(E_{X\cap P})=2$
. Obviously,
$a(E_{X\cap P})=2$
. Obviously,
and, respectively, on
![]() $(X\cap P)^+$
, we have
$(X\cap P)^+$
, we have
Arguing as in the transversal case, we note that the intersection
![]() $P\cap {\mathbb P}(R)$
is a general subspace of dimension
$P\cap {\mathbb P}(R)$
is a general subspace of dimension
![]() $k+l_X+2$
in
$k+l_X+2$
in
![]() ${\mathbb P}(R)$
. Taking into account that by the inequality (13), the inequality
${\mathbb P}(R)$
. Taking into account that by the inequality (13), the inequality
holds, and that by assumption
![]() $c_X\geqslant l_X+5$
, we see that
$c_X\geqslant l_X+5$
, we see that
![]() $R\cap P$
has a unique singularity, the point o. Furthermore, by the assumption about the rank of the singular point
$R\cap P$
has a unique singularity, the point o. Furthermore, by the assumption about the rank of the singular point
![]() $o\in R$
, we get the inequality
$o\in R$
, we get the inequality
so that
The exceptional divisor
![]() $E_{R\cap P}$
is the section of the subvariety
$E_{R\cap P}$
is the section of the subvariety
![]() $E_R\subset {\mathbb E}_R$
by a general linear subspace of dimension
$E_R\subset {\mathbb E}_R$
by a general linear subspace of dimension
![]() $k+l_X+1$
, whence we conclude that the variety
$k+l_X+1$
, whence we conclude that the variety
![]() $E_{R\cap P}$
is non-singular. Thus, we have shown that the singularity
$E_{R\cap P}$
is non-singular. Thus, we have shown that the singularity
![]() $o\in R\cap P$
is resolved by one blow-up. Therefore, the pair
$o\in R\cap P$
is resolved by one blow-up. Therefore, the pair
is canonical, so that the pair
is canonical, too. We have shown that
![]() $D\neq bR$
for
$D\neq bR$
for
![]() $b\geqslant 1$
.
$b\geqslant 1$
.
By inversion of adjunction for every
![]() $m\in I_X$
and a general subspace
$m\in I_X$
and a general subspace
![]() $P^{\sharp }\ni o$
of dimension m, the pair
$P^{\sharp }\ni o$
of dimension m, the pair
![]() $(X\cap P^{\sharp }, R\cap P^{\sharp })$
is canonical (recall that
$(X\cap P^{\sharp }, R\cap P^{\sharp })$
is canonical (recall that
![]() $n(R)=1$
). Repeating the arguments given in the transversal case (the proof of Proposition 3.1) word for word, we complete the proof of Proposition 3.2.
$n(R)=1$
). Repeating the arguments given in the transversal case (the proof of Proposition 3.1) word for word, we complete the proof of Proposition 3.2.
Remark 3.1. If for
![]() $l_X\leqslant k-1$
the intersection
$l_X\leqslant k-1$
the intersection
![]() $X\cap T_oX$
has the point o as a multi-quadratic singularity of type
$X\cap T_oX$
has the point o as a multi-quadratic singularity of type
![]() $2^k$
, the rank of which satisfies the inequality
$2^k$
, the rank of which satisfies the inequality
the assumption about the rank
![]() $\mathop {\mathrm {rk}}(o\in R)$
in the statement of Proposition 3.2 holds automatically for every tangent hyperplane at the point o.
$\mathop {\mathrm {rk}}(o\in R)$
in the statement of Proposition 3.2 holds automatically for every tangent hyperplane at the point o.
Theorem 3.2 (on the tangent hyperplane section).
Let
![]() $[X,o]$
be a marked complete intersection of level
$[X,o]$
be a marked complete intersection of level
![]() $(l_X,c_X)$
, where
$(l_X,c_X)$
, where
![]() $2\leqslant l_X\leqslant k-1$
and
$2\leqslant l_X\leqslant k-1$
and
![]() $c_X\geqslant l_X+7$
, and
$c_X\geqslant l_X+7$
, and
![]() $(X,D,o)$
a working triple. Let R be the section of X by a hyperplane which is tangent to X at the point o, and assume that R is not a component of the divisor D. Assume that the point
$(X,D,o)$
a working triple. Let R be the section of X by a hyperplane which is tangent to X at the point o, and assume that R is not a component of the divisor D. Assume that the point
![]() $o\in R$
is a multi-quadratic singularity of type
$o\in R$
is a multi-quadratic singularity of type
![]() $2^{l_R}$
, where
$2^{l_R}$
, where
![]() $l_R=l_X+1$
, the rank of which satisfies the inequality
$l_R=l_X+1$
, the rank of which satisfies the inequality
where
![]() $c_R=c_X-2$
, and also that the inequality
$c_R=c_X-2$
, and also that the inequality
![]() $\mathop {\mathrm {ct}}(R\backslash \mathop {\mathrm {Sing}}R)\geqslant 1$
holds. Then
$\mathop {\mathrm {ct}}(R\backslash \mathop {\mathrm {Sing}}R)\geqslant 1$
holds. Then
![]() $(R,(D\circ R),o)$
is a working triple on the marked complete intersection
$(R,(D\circ R),o)$
is a working triple on the marked complete intersection
![]() $[R,o]$
of level
$[R,o]$
of level
![]() $(l_R,c_R)$
.
$(l_R,c_R)$
.
Proof is similar to the transversal case (Theorem 3.1), and we just emphasize the necessary modifications. The fact that
![]() $[R,o]$
is a marked complete intersection of level
$[R,o]$
is a marked complete intersection of level
![]() $(l_R,c_R)$
is checked in the tangent case even easier than in the transversal one, because the assumption about the singularity
$(l_R,c_R)$
is checked in the tangent case even easier than in the transversal one, because the assumption about the singularity
![]() $o\in R$
is among the assumptions of the theorem.
$o\in R$
is among the assumptions of the theorem.
A general subspace
![]() $P\ni o$
of dimension
$P\ni o$
of dimension
![]() $k+c_R-1=k+c_X-3$
in
$k+c_R-1=k+c_X-3$
in
![]() ${\mathbb P}(R)$
is again presented as the intersection
${\mathbb P}(R)$
is again presented as the intersection
![]() $P=P^{\sharp }\cap {\mathbb P}(R)$
, where
$P=P^{\sharp }\cap {\mathbb P}(R)$
, where
![]() $P^{\sharp }\ni o$
is a general subspace of dimension
$P^{\sharp }\ni o$
is a general subspace of dimension
![]() $k+c_R\in I_X$
in
$k+c_R\in I_X$
in
![]() ${\mathbb P}(X)$
, and now, repeating the arguments in the transversal case and using inversion of adjunction, we get that
${\mathbb P}(X)$
, and now, repeating the arguments in the transversal case and using inversion of adjunction, we get that
![]() $(R,(D\circ R),o)$
is a working triple. Q.E.D. for the theorem.
$(R,(D\circ R),o)$
is a working triple. Q.E.D. for the theorem.
Proof of Proposition 1.7.
We assume that
![]() $l\leqslant k-1$
. Recall that the symbol T stands for the intersection
$l\leqslant k-1$
. Recall that the symbol T stands for the intersection
![]() $F\cap T_oF$
; this is a subvariety of codimension
$F\cap T_oF$
; this is a subvariety of codimension
![]() $(k-l)$
in F. Let us construct a sequence of subvarieties
$(k-l)$
in F. Let us construct a sequence of subvarieties
where
![]() $T_{i+1}$
is the section of
$T_{i+1}$
is the section of
![]() $T_i\ni o$
by some hyperplane
$T_i\ni o$
by some hyperplane
![]() ${\mathbb P}(T_{i+1})=\langle T_{i+1}\rangle \ni o$
, which is tangent to
${\mathbb P}(T_{i+1})=\langle T_{i+1}\rangle \ni o$
, which is tangent to
![]() $T_i$
at the point o. Theorem 1.1 implies that the inequality
$T_i$
at the point o. Theorem 1.1 implies that the inequality
holds (the inequality of Theorem 1.1 for the codimension
![]() $c_F$
is much stronger, but for the clarity of exposition, we give the weakest estimate that is sufficient for the proof of Proposition 1.7; this remark also applies to the estimate of the rank of the multi-quadratic singularity
$c_F$
is much stronger, but for the clarity of exposition, we give the weakest estimate that is sufficient for the proof of Proposition 1.7; this remark also applies to the estimate of the rank of the multi-quadratic singularity
![]() $o\in T$
below). Furthermore, the condition (MQ2) implies that
$o\in T$
below). Furthermore, the condition (MQ2) implies that
![]() $o\in T$
is a multi-quadratic singularity of type
$o\in T$
is a multi-quadratic singularity of type
![]() $2^k$
, and moreover, the inequality
$2^k$
, and moreover, the inequality
holds. Finally, by Theorem 1.2 for every hyperplane section W of every subvariety
![]() $T_i$
,
$T_i$
,
![]() $i=0,1,\dots ,k-l$
, every non-singular point
$i=0,1,\dots ,k-l$
, every non-singular point
![]() $p\in W$
and every prime divisor Y on W the inequality
$p\in W$
and every prime divisor Y on W the inequality
holds. Then for all
![]() $i=0,1,\dots ,k-l$
, the pair
$i=0,1,\dots ,k-l$
, the pair
![]() $[T_i,o]$
is a marked complete intersection of level
$[T_i,o]$
is a marked complete intersection of level
Indeed, the inequality
![]() $c_i\geqslant l_i+4$
is true by the definition of the numbers
$c_i\geqslant l_i+4$
is true by the definition of the numbers
![]() $l_i$
,
$l_i$
,
![]() $c_i$
, the condition (MC1) follows from Remark 1.4, the point
$c_i$
, the condition (MC1) follows from Remark 1.4, the point
![]() $o\in T_i$
by construction is a multi-quadratic singularity of type
$o\in T_i$
by construction is a multi-quadratic singularity of type
![]() $2^{l+1}$
, and moreover, by (15), we have
$2^{l+1}$
, and moreover, by (15), we have
and, finally, repeating the proof of Proposition 1.1 and the arguments of Subsection 1.5 word for word, we get that by (16), the condition (MC3) holds. Therefore,
![]() $[T,o]$
is a marked complete intersection of level
$[T,o]$
is a marked complete intersection of level
![]() $(k,c_{k-l})$
, where
$(k,c_{k-l})$
, where
![]() $c_{k-l}=c_F-2(k-l)\geqslant k+4$
. Recall (Proposition 1.6) that
$c_{k-l}=c_F-2(k-l)\geqslant k+4$
. Recall (Proposition 1.6) that
![]() $c_F=4k+2\varepsilon (k)$
. Since
$c_F=4k+2\varepsilon (k)$
. Since
![]() $l\geqslant 2$
, the inequality
$l\geqslant 2$
, the inequality
holds, so that
![]() $[T,o]$
is a marked complete intersection of level
$[T,o]$
is a marked complete intersection of level
![]() $(k,c_T)$
, as we claimed.
$(k,c_T)$
, as we claimed.
It remains to construct the working triple
![]() $(T,D_T,o)$
. We will construct a sequence of working triples
$(T,D_T,o)$
. We will construct a sequence of working triples
![]() $(T_i,D_i,o)$
, where
$(T_i,D_i,o)$
, where
![]() $i=0,1,\dots ,k-l$
and
$i=0,1,\dots ,k-l$
and
![]() $D_0=D_F$
. Assume that
$D_0=D_F$
. Assume that
![]() $(T_i,D_i,o)$
is already constructed and
$(T_i,D_i,o)$
is already constructed and
![]() $i\leqslant k-l-1$
. Let us check that all assumptions that allow us to apply Proposition 3.2 are satisfied.
$i\leqslant k-l-1$
. Let us check that all assumptions that allow us to apply Proposition 3.2 are satisfied.
Indeed, the fact that
![]() $i\leqslant k-l-1$
implies the inequality
$i\leqslant k-l-1$
implies the inequality
![]() $c_i\geqslant l_i+7$
. The point
$c_i\geqslant l_i+7$
. The point
![]() $o\in T_{i+1}$
is a multi-quadratic singularity of type
$o\in T_{i+1}$
is a multi-quadratic singularity of type
![]() $2^{l_i+1}$
, the rank of which satisfies the inequality
$2^{l_i+1}$
, the rank of which satisfies the inequality
(see above). Applying Proposition 3.2, we remove
![]() $T_{i+1}$
from the effective divisor
$T_{i+1}$
from the effective divisor
![]() $D_i$
(if it is necessary) and obtain the working triple
$D_i$
(if it is necessary) and obtain the working triple
![]() $(T_i,D^*_i,o)$
, where the effective divisor
$(T_i,D^*_i,o)$
, where the effective divisor
![]() $D^*_i$
does not contain
$D^*_i$
does not contain
![]() $T_{i+1}$
as a component.
$T_{i+1}$
as a component.
It is easy to see that we have all assumptions of Theorem 3.2. Set
Now
![]() $(T_{i+1}, D_{i+1}, o)$
is a working triple. Proof of Proposition 1.7 is complete.
$(T_{i+1}, D_{i+1}, o)$
is a working triple. Proof of Proposition 1.7 is complete.
3.5 Plan of the proof of Proposition 1.8
Recall that by the condition (MQ2), the inequality
holds. The pair
![]() $[T,o]$
is a marked complete intersection of level
$[T,o]$
is a marked complete intersection of level
![]() $(k,c_T)$
, where
$(k,c_T)$
, where
![]() $c_T=2k+2\varepsilon (k)+4$
. Let
$c_T=2k+2\varepsilon (k)+4$
. Let
where
![]() $a\leqslant \varepsilon (k)$
, be an arbitrary sequence of subvarieties in T, where
$a\leqslant \varepsilon (k)$
, be an arbitrary sequence of subvarieties in T, where
![]() $R_{i+1}$
is the section of
$R_{i+1}$
is the section of
![]() $R_i$
by the hyperplane
$R_i$
by the hyperplane
![]() ${\mathbb P}(R_{i+1})$
in
${\mathbb P}(R_{i+1})$
in
![]() ${\mathbb P}(R_i)$
, containing the point o. Set
${\mathbb P}(R_i)$
, containing the point o. Set
![]() $c_i=c_T-2i$
, where
$c_i=c_T-2i$
, where
![]() $i=0,1,\dots ,a$
.
$i=0,1,\dots ,a$
.
Proposition 3.3. The pair
![]() $[R_i,o]$
is a marked complete intersection of level
$[R_i,o]$
is a marked complete intersection of level
![]() $(k,c_i)$
.
$(k,c_i)$
.
Proof. Since
![]() $a\leqslant \varepsilon (k)$
, the inequality
$a\leqslant \varepsilon (k)$
, the inequality
![]() $c_i\geqslant k+4$
holds in an obvious way (in fact,
$c_i\geqslant k+4$
holds in an obvious way (in fact,
![]() $c_i\geqslant 2k+4)$
. The condition (MC1) holds by Remark 1.4. The condition (MC3) is obtained by repeating the proof of Proposition 1.1 and the arguments of Subsection 1.5 word for word, taking into account Theorem 1.2. Finally, again by Remark 1.4, the inequality
$c_i\geqslant 2k+4)$
. The condition (MC1) holds by Remark 1.4. The condition (MC3) is obtained by repeating the proof of Proposition 1.1 and the arguments of Subsection 1.5 word for word, taking into account Theorem 1.2. Finally, again by Remark 1.4, the inequality
implies the condition (MC2). Q.E.D. for the proposition.
Now let us construct for every
![]() $i=0,1,\dots ,a$
an effective divisor
$i=0,1,\dots ,a$
an effective divisor
![]() $D_i$
on
$D_i$
on
![]() $R_i$
in the same way as we did it in Subsection 3.4 in the proof of Proposition 1.7, applying instead of Proposition 3.2, its ‘transversal’ analog, Proposition 3.1, and Theorem 3.1 instead of Theorem 3.2. More precisely, if the effective divisor
$R_i$
in the same way as we did it in Subsection 3.4 in the proof of Proposition 1.7, applying instead of Proposition 3.2, its ‘transversal’ analog, Proposition 3.1, and Theorem 3.1 instead of Theorem 3.2. More precisely, if the effective divisor
![]() $D_i$
, where
$D_i$
, where
![]() $i\leqslant a-1$
, is already constructed, we remove from this divisor all components that are hyperplane sections (if there are such components), and obtain an effective divisor
$i\leqslant a-1$
, is already constructed, we remove from this divisor all components that are hyperplane sections (if there are such components), and obtain an effective divisor
![]() $D^*_i$
that does not contain hyperplane sections as components, and such that
$D^*_i$
that does not contain hyperplane sections as components, and such that
![]() $(R_i,D^*_i,o)$
is a working triple (Proposition 3.1).
$(R_i,D^*_i,o)$
is a working triple (Proposition 3.1).
Proposition 3.4. The following inequality holds:
 $$ \begin{align*}\frac{\nu(D^*_i)}{n(D^*_i)}\geqslant\frac{\nu(D_i)}{n(D_i)}. \end{align*} $$
$$ \begin{align*}\frac{\nu(D^*_i)}{n(D^*_i)}\geqslant\frac{\nu(D_i)}{n(D_i)}. \end{align*} $$
Proof. It is sufficient to consider the case when
![]() $D^*_i$
is obtained from
$D^*_i$
is obtained from
![]() $D_i$
by removing one hyperplane section
$D_i$
by removing one hyperplane section
![]() $Z\ni o$
. Write down
$Z\ni o$
. Write down
where
![]() $b\geqslant 1$
. Since
$b\geqslant 1$
. Since
![]() $c_i\geqslant 2k+4$
, we can apply Proposition 1.5:
$c_i\geqslant 2k+4$
, we can apply Proposition 1.5:
![]() $\nu (D_i)>n(D_i)$
. However,
$\nu (D_i)>n(D_i)$
. However,
![]() $\nu (Z)=n(Z)=1$
. Set
$\nu (Z)=n(Z)=1$
. Set
![]() $\nu (D_i)=\alpha n(D_i)$
, where
$\nu (D_i)=\alpha n(D_i)$
, where
![]() $\alpha>1$
. We get
$\alpha>1$
. We get
 $$ \begin{align*}\frac{\nu(D^*_i)}{n(D^*_i)}= \frac{\alpha n(D^*_i)+(\alpha-1)b}{n(D^*_i)}>\alpha, \end{align*} $$
$$ \begin{align*}\frac{\nu(D^*_i)}{n(D^*_i)}= \frac{\alpha n(D^*_i)+(\alpha-1)b}{n(D^*_i)}>\alpha, \end{align*} $$
which proves the proposition. Q.E.D.
(If we remove from
![]() $D_i$
, a hyperplane section that does not contain the point o, the claim of Proposition 3.4 is trivial.)
$D_i$
, a hyperplane section that does not contain the point o, the claim of Proposition 3.4 is trivial.)
Now we apply Theorem 3.1, setting
![]() $D_{i+1}=(D^*_i\circ R_{i+1})$
. This cycle of the scheme-theoretic intersection is well defined as an effective divisor on
$D_{i+1}=(D^*_i\circ R_{i+1})$
. This cycle of the scheme-theoretic intersection is well defined as an effective divisor on
![]() $R_{i+1}$
, and moreover,
$R_{i+1}$
, and moreover,
![]() $(R_{i+1}, D_{i+1}, o)$
is a working triple and
$(R_{i+1}, D_{i+1}, o)$
is a working triple and
 $$ \begin{align*}\frac{\nu(D_{i+1})}{n(D_{i+1})}\geqslant\frac{\nu(D^*_i)}{n(D^*_i)} \geqslant\frac{\nu(D_i)}{n(D_i)}. \end{align*} $$
$$ \begin{align*}\frac{\nu(D_{i+1})}{n(D_{i+1})}\geqslant\frac{\nu(D^*_i)}{n(D^*_i)} \geqslant\frac{\nu(D_i)}{n(D_i)}. \end{align*} $$
We emphasize that
![]() $R_1,\dots , R_a$
is an arbitrary sequence of consecutive hyperplane sections. By Remark 1.4, for all
$R_1,\dots , R_a$
is an arbitrary sequence of consecutive hyperplane sections. By Remark 1.4, for all
![]() $i=0,1,\dots ,a$
, the inequality
$i=0,1,\dots ,a$
, the inequality
![]() $c_i\geqslant 2k+4$
holds, and the rank of the multi-quadratic singularity
$c_i\geqslant 2k+4$
holds, and the rank of the multi-quadratic singularity
![]() $o\in R_i$
of type
$o\in R_i$
of type
![]() $2^k$
is at least
$2^k$
is at least
![]() $10k^2+8k+5$
. By Theorem 1.4 and Proposition 1.5, we have the inequalities
$10k^2+8k+5$
. By Theorem 1.4 and Proposition 1.5, we have the inequalities
Therefore, at every step of our construction, the assumptions of the following claim are satisfied.
Theorem 3.3 (on the special hyperplane section).
Let
![]() $[X,o]$
be a marked complete intersection of level
$[X,o]$
be a marked complete intersection of level
![]() $(k,c_X)$
, where
$(k,c_X)$
, where
![]() $c_X\geqslant 2k+4$
and the inequality
$c_X\geqslant 2k+4$
and the inequality
holds. Let
![]() $(X,D,o)$
be a working triple, where the effective divisor D does not contain hyperplane sections and satisfies the inequalities
$(X,D,o)$
be a working triple, where the effective divisor D does not contain hyperplane sections and satisfies the inequalities
Then there is a section
![]() $R\ni o$
of the variety X by a hyperplane
$R\ni o$
of the variety X by a hyperplane
![]() ${\mathbb P}(R)=\langle R\rangle \subset {\mathbb P}(X)= {\mathbb P}^{N(X)}$
, such that the effective divisor
${\mathbb P}(R)=\langle R\rangle \subset {\mathbb P}(X)= {\mathbb P}^{N(X)}$
, such that the effective divisor
![]() $D_R=(R\circ D)$
on R satisfies the inequality
$D_R=(R\circ D)$
on R satisfies the inequality
 $$ \begin{align*}2-\frac{\nu(D_R)}{n(D_R)}<\frac{1}{1+\frac{1}{k}}\left(2- \frac{\nu(D)}{n(D)}\right). \end{align*} $$
$$ \begin{align*}2-\frac{\nu(D_R)}{n(D_R)}<\frac{1}{1+\frac{1}{k}}\left(2- \frac{\nu(D)}{n(D)}\right). \end{align*} $$
Now by the definition of the integer
![]() $\varepsilon (k)$
and what was said above, Theorem 3.3 immediately implies Proposition 1.8.
$\varepsilon (k)$
and what was said above, Theorem 3.3 immediately implies Proposition 1.8.
4 Multi-quadratic singularities
In this section, we consider the properties of multi-quadratic singularities, the rank of which is bounded from below: they are factorial, stable with respect to blow-ups and terminal. In Subsection 4.5, we study linear subspaces on complete intersections of quadrics and the properties of projections from these subspaces.
4.1 The definition and the first properties
Let
![]() ${\cal X}$
be an (irreducible) algebraic variety,
${\cal X}$
be an (irreducible) algebraic variety,
![]() $o\in {\cal X}$
a point.
$o\in {\cal X}$
a point.
Definition 4.1. The point o is a multi-quadratic singularity of the variety
![]() ${\cal X}$
of type
${\cal X}$
of type
![]() $2^l$
and rank
$2^l$
and rank
![]() $r\geqslant 1$
, if in some neighborhood of this point,
$r\geqslant 1$
, if in some neighborhood of this point,
![]() ${\cal X}$
can be realized as a subvariety of a non-singular
${\cal X}$
can be realized as a subvariety of a non-singular
![]() $N=(\mathop {\mathrm {dim}} {\cal X}+ l)$
-dimensional variety
$N=(\mathop {\mathrm {dim}} {\cal X}+ l)$
-dimensional variety
![]() ${\cal Y}\ni o$
, and for some system
${\cal Y}\ni o$
, and for some system
![]() $(u_1, \dots , u_N)$
of local parameters on
$(u_1, \dots , u_N)$
of local parameters on
![]() ${\cal Y}$
at the point o, the subvariety
${\cal Y}$
at the point o, the subvariety
![]() ${\cal X}$
is the scheme of common zeros of regular functions
${\cal X}$
is the scheme of common zeros of regular functions
which are represented by the formal power series
where
![]() $\alpha _{i,j}(u_1,\dots ,u_N)$
are homogeneous polynomials of degree j and
$\alpha _{i,j}(u_1,\dots ,u_N)$
are homogeneous polynomials of degree j and
(Obviously, the order of the formal power series, representing
![]() $\alpha _i$
, and the rank of the tuple of quadratic forms
$\alpha _i$
, and the rank of the tuple of quadratic forms
![]() $\alpha _{i,2}$
do not depend on the choice of the local parameters on
$\alpha _{i,2}$
do not depend on the choice of the local parameters on
![]() ${\cal Y}$
at the point o.)
${\cal Y}$
at the point o.)
It is convenient to work in a more general context. Assume that in a neighborhood of the point o, the variety
![]() ${\cal X}$
is realized as a subvariety
${\cal X}$
is realized as a subvariety
![]() ${\cal X}\subset {\cal Z}$
, where
${\cal X}\subset {\cal Z}$
, where
![]() $\mathop {\mathrm {dim}}{\cal Z}=\mathop {\mathrm {dim}}{\cal X}+e=N({\cal Z})$
, and for a certain system of local parameters
$\mathop {\mathrm {dim}}{\cal Z}=\mathop {\mathrm {dim}}{\cal X}+e=N({\cal Z})$
, and for a certain system of local parameters
![]() $(v_1,\dots ,v_{N({\cal Z})})$
on
$(v_1,\dots ,v_{N({\cal Z})})$
on
![]() ${\cal Z}$
at the point o, the subvariety
${\cal Z}$
at the point o, the subvariety
![]() ${\cal X}$
is the scheme of common zeros of regular functions
${\cal X}$
is the scheme of common zeros of regular functions
which are represented by the formal power series
where
![]() $\beta _{i,j}(v_*)$
are homogeneous polynomials of degree j. Assume that for some
$\beta _{i,j}(v_*)$
are homogeneous polynomials of degree j. Assume that for some
![]() $l\in \{0,1,\dots ,e\},$
$l\in \{0,1,\dots ,e\},$
where we assume (for the convenience of notations) that the linear forms
![]() $\beta _{j,1}$
for
$\beta _{j,1}$
for
![]() $l+1\leqslant j\leqslant e$
are linearly independent, so that for
$l+1\leqslant j\leqslant e$
are linearly independent, so that for
![]() $1\leqslant i\leqslant l$
and
$1\leqslant i\leqslant l$
and
![]() $l+1\leqslant j\leqslant e$
, there are uniquely determined numbers
$l+1\leqslant j\leqslant e$
, there are uniquely determined numbers
![]() $a_{i,j}$
, such that
$a_{i,j}$
, such that
 $$ \begin{align*}\beta_{i,1}=\sum^e_{j=l+1}a_{i,j}\beta_{j,1}. \end{align*} $$
$$ \begin{align*}\beta_{i,1}=\sum^e_{j=l+1}a_{i,j}\beta_{j,1}. \end{align*} $$
Set
![]() ${\cal Y}=\{\beta _j=0\,|\, l+1\leqslant j\leqslant e\}$
and
${\cal Y}=\{\beta _j=0\,|\, l+1\leqslant j\leqslant e\}$
and
 $$ \begin{align*}\beta_i^*=\beta_i-\sum_{j=l+1}^e a_{i,j}\beta_j. \end{align*} $$
$$ \begin{align*}\beta_i^*=\beta_i-\sum_{j=l+1}^e a_{i,j}\beta_j. \end{align*} $$
Then (in a neighborhood of the point o) the variety
![]() ${\cal Y}$
is non-singular, and
${\cal Y}$
is non-singular, and
![]() ${\cal X}\subset {\cal Y}$
is realized as the scheme of common zeros of the regular functions
${\cal X}\subset {\cal Y}$
is realized as the scheme of common zeros of the regular functions
![]() $\beta ^*_i$
,
$\beta ^*_i$
,
![]() $1\leqslant i\leqslant l$
. Set
$1\leqslant i\leqslant l$
. Set
If
then obviously
![]() $o\in {\cal X}$
is a multi-quadratic singularity of rank r.
$o\in {\cal X}$
is a multi-quadratic singularity of rank r.
The rank of the multi-quadratic point
![]() $o\in {\cal X}$
is denoted by the symbol
$o\in {\cal X}$
is denoted by the symbol
![]() $\mathop {\mathrm {rk}} (o\in {\cal X})$
or just
$\mathop {\mathrm {rk}} (o\in {\cal X})$
or just
![]() $\mathop {\mathrm {rk}}(o)$
, if it is clear which variety is meant. For uniformity of notations, we treat a non-singular point as a multi-quadratic one of type
$\mathop {\mathrm {rk}}(o)$
, if it is clear which variety is meant. For uniformity of notations, we treat a non-singular point as a multi-quadratic one of type
![]() $2^0$
.
$2^0$
.
Proposition 4.1. Assume that
![]() $o\in {\cal X}$
is a multi-quadratic singularity of type
$o\in {\cal X}$
is a multi-quadratic singularity of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\geqslant 1$
, and of rank
$l\geqslant 1$
, and of rank
![]() $r\geqslant 2l$
. Then in a neighborhood of the point o, every point
$r\geqslant 2l$
. Then in a neighborhood of the point o, every point
![]() $p\in {\cal X}$
is either non-singular or a multi-quadratic of type
$p\in {\cal X}$
is either non-singular or a multi-quadratic of type
![]() $2^b$
, where
$2^b$
, where
![]() $b\in \{1,\dots ,l\}$
, of rank
$b\in \{1,\dots ,l\}$
, of rank
![]() $\geqslant r-2(l-b)$
.
$\geqslant r-2(l-b)$
.
Proof. Using the notations for the embedding
![]() ${\cal X}\subset {\cal Z}$
introduced above, with
${\cal X}\subset {\cal Z}$
introduced above, with
![]() $e=l$
(so that
$e=l$
(so that
![]() $\beta _{i,1}=0$
for all
$\beta _{i,1}=0$
for all
![]() $i=1,\dots ,l$
) and setting
$i=1,\dots ,l$
) and setting
![]() $N({\cal Z})=N$
, consider an open set
$N({\cal Z})=N$
, consider an open set
![]() $U\subset {\cal Z}$
,
$U\subset {\cal Z}$
,
![]() $U\ni o$
, such that for every point
$U\ni o$
, such that for every point
![]() $p\in U$
, the ‘shifted’ functions
$p\in U$
, the ‘shifted’ functions
form a system of local parameters at the point p, and in the formal expansion
with respect to the system of parameters
![]() $v^{(p)}_*$
, the quadratic components satisfy the inequality
$v^{(p)}_*$
, the quadratic components satisfy the inequality
If the point p is a common zero of
![]() $\beta _1,\dots ,\beta _l$
, then
$\beta _1,\dots ,\beta _l$
, then
![]() $\beta ^{(p)}_{i,0}=0$
for
$\beta ^{(p)}_{i,0}=0$
for
![]() $1\leqslant i\leqslant l$
. Set
$1\leqslant i\leqslant l$
. Set
and assume (for the convenience of notations) that the forms
![]() $\beta ^{(p)}_{i,1}$
for
$\beta ^{(p)}_{i,1}$
for
![]() $b+1\leqslant i\leqslant l$
are linearly independent, where
$b+1\leqslant i\leqslant l$
are linearly independent, where
Since
![]() $\mathop {\mathrm {codim}}(T_p{\cal X}\subset T_p{\cal Z})=l-b$
, by Remark 1.4, the inequality
$\mathop {\mathrm {codim}}(T_p{\cal X}\subset T_p{\cal Z})=l-b$
, by Remark 1.4, the inequality
holds. It is easy to see from the construction of the quadratic forms
![]() $\beta ^{(p)*}_{i,2}$
,
$\beta ^{(p)*}_{i,2}$
,
![]() $1\leqslant i\leqslant b$
that every linear combination of these forms with coefficients
$1\leqslant i\leqslant b$
that every linear combination of these forms with coefficients
![]() $(\lambda _1,\dots ,\lambda _b)\neq (0,\dots ,0)$
is a linear combination of the original forms
$(\lambda _1,\dots ,\lambda _b)\neq (0,\dots ,0)$
is a linear combination of the original forms
![]() $\beta ^{(p)}_{i,2}$
,
$\beta ^{(p)}_{i,2}$
,
![]() $1\leqslant i\leqslant l$
, not all coefficients in which are equal to zero. Therefore, the point p is a multi-quadratic singularity of rank
$1\leqslant i\leqslant l$
, not all coefficients in which are equal to zero. Therefore, the point p is a multi-quadratic singularity of rank
![]() $\geqslant r-2(l-b)$
, as we claimed. Q.E.D. for the proposition.
$\geqslant r-2(l-b)$
, as we claimed. Q.E.D. for the proposition.
4.2 Complete intersections of quadrics
In the notations of Definition 4.1, let
![]() ${\cal Y}^+\to {\cal Y}$
be the blow-up of the point o with the exceptional divisor
${\cal Y}^+\to {\cal Y}$
be the blow-up of the point o with the exceptional divisor
![]() $E_{\cal Y}\cong {\mathbb P}^{N-1}$
and
$E_{\cal Y}\cong {\mathbb P}^{N-1}$
and
![]() ${\cal X}^+\subset {\cal Y}^+$
the strict transform of
${\cal X}^+\subset {\cal Y}^+$
the strict transform of
![]() ${\cal X}$
on
${\cal X}$
on
![]() ${\cal Y}^+$
, so that
${\cal Y}^+$
, so that
![]() ${\cal X}^+\to {\cal X}$
is the blow-up of the point o on
${\cal X}^+\to {\cal X}$
is the blow-up of the point o on
![]() ${\cal X}$
with the exceptional divisor
${\cal X}$
with the exceptional divisor
![]() $E_{\cal Y}|_{{\cal X}^+}=E_{\cal X}$
. Therefore,
$E_{\cal Y}|_{{\cal X}^+}=E_{\cal X}$
. Therefore,
![]() $E_{\cal X}$
is the scheme of common zeros of the quadratic forms
$E_{\cal X}$
is the scheme of common zeros of the quadratic forms
![]() $\alpha _{i,2}$
,
$\alpha _{i,2}$
,
![]() $i=1,\dots ,l$
, on
$i=1,\dots ,l$
, on
![]() $E_{\cal Y}\cong {\mathbb P}^{N-1}$
.
$E_{\cal Y}\cong {\mathbb P}^{N-1}$
.
Let
![]() $q_1,\dots ,q_l$
be quadratic forms on
$q_1,\dots ,q_l$
be quadratic forms on
![]() ${\mathbb P}^{N-1}$
, where
${\mathbb P}^{N-1}$
, where
![]() $N\geqslant l+4$
. By the symbol
$N\geqslant l+4$
. By the symbol
![]() $q_{[1,l]}$
, we denote the tuple
$q_{[1,l]}$
, we denote the tuple
![]() $(q_1,\dots ,q_l)$
.
$(q_1,\dots ,q_l)$
.
Proposition 4.2. (i) Assume that the inequality
holds. Then the scheme of common zeros of the forms
![]() $q_1,\dots ,q_l$
is an irreducible non-degenerate factorial variety
$q_1,\dots ,q_l$
is an irreducible non-degenerate factorial variety
![]() $Q\subset {\mathbb P}^{N-1}$
of codimension l – that is, a complete intersection of type
$Q\subset {\mathbb P}^{N-1}$
of codimension l – that is, a complete intersection of type
![]() $2^l$
.
$2^l$
.
(ii) Assume that for some
![]() $e\geqslant 4$
, the inequality
$e\geqslant 4$
, the inequality
holds. Then the following inequality is true:
Proof is given below in Subsection 4.4.
Corollary 4.1.
(i) Assume that the rank of the tuple
![]() $\alpha _{*,2}=(\alpha _{1,2},\dots ,\alpha _{l,2})$
of quadratic forms satisfies the inequality
$\alpha _{*,2}=(\alpha _{1,2},\dots ,\alpha _{l,2})$
of quadratic forms satisfies the inequality
Then in a neighborhood of the point o, the scheme of common zeros of the regular functions
![]() $\alpha _1,\dots ,\alpha _l$
is an irreducible reduced factorial subvariety
$\alpha _1,\dots ,\alpha _l$
is an irreducible reduced factorial subvariety
![]() ${\cal X}$
of codimension l in
${\cal X}$
of codimension l in
![]() ${\cal Y}$
.
${\cal Y}$
.
(ii) Assume that for some
![]() $e\geqslant 4$
, the inequality
$e\geqslant 4$
, the inequality
holds. Then in a neighborhood of the point o, the following inequality is true:
Proof. Both claims obviously follow from Proposition 4.2, taking into account Grothendieck’s theorem [Reference Call and Lyubeznik21] on the factoriality of a complete intersection, the singular set of which is of codimension
![]() $\geqslant 4$
.
$\geqslant 4$
.
Therefore, for
![]() $r\geqslant 2l+3$
, the assumption in Definition 4.1, that
$r\geqslant 2l+3$
, the assumption in Definition 4.1, that
![]() ${\cal X}$
is an irreducible variety, is unnecessary: in a neighborhood of the point o, the scheme of common zeros of the functions
${\cal X}$
is an irreducible variety, is unnecessary: in a neighborhood of the point o, the scheme of common zeros of the functions
![]() $\alpha _*$
is automatically irreducible and reduced, and moreover, it is a factorial variety. This proves all claims of Theorem 1.1, except for that the singularities of the variety F are terminal.
$\alpha _*$
is automatically irreducible and reduced, and moreover, it is a factorial variety. This proves all claims of Theorem 1.1, except for that the singularities of the variety F are terminal.
4.3 Stability with respect to blow-ups
Let
![]() $\underline {r}=(r_1,r_2,\dots ,r_k)$
be a tuple of integers, satisfying the inequalities
$\underline {r}=(r_1,r_2,\dots ,r_k)$
be a tuple of integers, satisfying the inequalities
![]() $r_{i+1}\geqslant r_i+2$
for
$r_{i+1}\geqslant r_i+2$
for
![]() $i=1,\dots ,k-1$
, where
$i=1,\dots ,k-1$
, where
![]() $r_1\geqslant 5$
. Again, let
$r_1\geqslant 5$
. Again, let
![]() ${\cal Y}$
be a non-singular N-dimensional variety, where
${\cal Y}$
be a non-singular N-dimensional variety, where
![]() $N\geqslant k+3$
, and
$N\geqslant k+3$
, and
![]() ${\cal X}\subset {\cal Y}$
an (irreducible) subvariety of codimension k, every point
${\cal X}\subset {\cal Y}$
an (irreducible) subvariety of codimension k, every point
![]() $o\in {\cal X}$
of which is either non-singular or a multi-quadratic singularity of type
$o\in {\cal X}$
of which is either non-singular or a multi-quadratic singularity of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\in \{1,\dots ,k\}$
, of rank
$l\in \{1,\dots ,k\}$
, of rank
![]() $\geqslant r_l$
. Somewhat abusing the terminology, we say in this case that
$\geqslant r_l$
. Somewhat abusing the terminology, we say in this case that
![]() ${\cal X}$
has multi-quadratic singularities of type
${\cal X}$
has multi-quadratic singularities of type
![]() $\underline {r}$
.
$\underline {r}$
.
Theorem 4.1. In the assumptions above, let
![]() $B\subset {\cal X}$
be an irreducible subvariety of codimension
$B\subset {\cal X}$
be an irreducible subvariety of codimension
![]() $\geqslant 2$
. Then there is an open subset
$\geqslant 2$
. Then there is an open subset
![]() $U\subset {\cal X}$
, such that
$U\subset {\cal X}$
, such that
![]() $U\cap B\neq \emptyset $
,
$U\cap B\neq \emptyset $
,
![]() $U\cap B$
is non-singular and the blow-up
$U\cap B$
is non-singular and the blow-up
along B gives a quasi-projective variety
![]() $U_B$
with multi-quadratic singularities of type
$U_B$
with multi-quadratic singularities of type
![]() $\underline {r}$
.
$\underline {r}$
.
Proof. If a point of general position
![]() $o\in B$
is non-singular on
$o\in B$
is non-singular on
![]() ${\cal X}$
, there is nothing to prove. If
${\cal X}$
, there is nothing to prove. If
![]() $o\in {\cal X}$
is a multi-quadratic singularity of type
$o\in {\cal X}$
is a multi-quadratic singularity of type
![]() $2^l$
, where
$2^l$
, where
![]() $l<k$
, then a certain Zariski open subset
$l<k$
, then a certain Zariski open subset
![]() $U\subset {\cal X}$
,
$U\subset {\cal X}$
,
![]() $U\ni o$
has multi-quadratic singularities of type
$U\ni o$
has multi-quadratic singularities of type
![]() $(r_1,\dots ,r_l)$
(see Subsection 4.1), so that it is sufficient to consider the case when a point of general position
$(r_1,\dots ,r_l)$
(see Subsection 4.1), so that it is sufficient to consider the case when a point of general position
![]() $o\in B$
is a multi-quadratic point of type
$o\in B$
is a multi-quadratic point of type
![]() $2^k$
on
$2^k$
on
![]() ${\cal X}$
. Passing over to an open subset, we may assume that the subvariety B is non-singular. Let
${\cal X}$
. Passing over to an open subset, we may assume that the subvariety B is non-singular. Let
![]() $(u_1,\dots ,u_N)$
be a system of local parameters at the point o, such that
$(u_1,\dots ,u_N)$
be a system of local parameters at the point o, such that
![]() $B=\{u_1=\dots =u_m=0\}$
. Since
$B=\{u_1=\dots =u_m=0\}$
. Since
![]() $B\subset {\cal X}$
, the subvariety
$B\subset {\cal X}$
, the subvariety
![]() ${\cal X}\subset {\cal Y}$
is the scheme of common zeros of regular functions
${\cal X}\subset {\cal Y}$
is the scheme of common zeros of regular functions
where for all
![]() $i=1,\dots ,k$
,
$i=1,\dots ,k$
,
where
![]() $\beta _{i,j}$
are homogeneous polynomials of degree j in
$\beta _{i,j}$
are homogeneous polynomials of degree j in
![]() $u_1,\dots ,u_m$
with coefficients from
$u_1,\dots ,u_m$
with coefficients from
![]() ${\cal O}_{o,B}$
. Again replacing
${\cal O}_{o,B}$
. Again replacing
![]() ${\cal Y}$
, if necessary, by an open subset, containing the point o, we have
${\cal Y}$
, if necessary, by an open subset, containing the point o, we have
so that all coefficients of the forms
![]() $\beta _{i,j}$
are regular functions on B; in particular,
$\beta _{i,j}$
are regular functions on B; in particular,
 $$ \begin{align*}\beta_{i,2}=\sum_{1\leqslant j_1\leqslant j_2\leqslant m}A_{j_1,j_2}u_{j_1}u_{j_2}, \end{align*} $$
$$ \begin{align*}\beta_{i,2}=\sum_{1\leqslant j_1\leqslant j_2\leqslant m}A_{j_1,j_2}u_{j_1}u_{j_2}, \end{align*} $$
where
![]() $A_{j_1,j_2}\in {\cal O}(B)$
. In terms of the embedding
$A_{j_1,j_2}\in {\cal O}(B)$
. In terms of the embedding
![]() ${\cal O}_{o,{\cal Y}}\subset {\mathbb C}[[u_1,\dots ,u_N]]$
, we get the presentation
${\cal O}_{o,{\cal Y}}\subset {\mathbb C}[[u_1,\dots ,u_N]]$
, we get the presentation
where
![]() $\overline {\beta }_{i,j}$
is a homogeneous polynomial of degree j in
$\overline {\beta }_{i,j}$
is a homogeneous polynomial of degree j in
![]() $u_*$
, and moreover, in the right-hand side, there are no monomials that do not contain the variables
$u_*$
, and moreover, in the right-hand side, there are no monomials that do not contain the variables
![]() $u_1,\dots ,u_m$
, or that contain precisely one of them (in the power 1): every monomial in the right-hand side is divisible by some quadratic monomial in
$u_1,\dots ,u_m$
, or that contain precisely one of them (in the power 1): every monomial in the right-hand side is divisible by some quadratic monomial in
![]() $u_1,\dots ,u_m$
.
$u_1,\dots ,u_m$
.
Let
![]() ${\cal Y}_B\to {\cal Y}$
be the blow-up of the subvariety B and
${\cal Y}_B\to {\cal Y}$
be the blow-up of the subvariety B and
![]() ${\cal X}_B\subset {\cal Y}_B$
the strict transform of
${\cal X}_B\subset {\cal Y}_B$
the strict transform of
![]() ${\cal X}$
. Obviously, the morphism
${\cal X}$
. Obviously, the morphism
![]() ${\cal X}_B\to {\cal X}$
is the blow-up of B on
${\cal X}_B\to {\cal X}$
is the blow-up of B on
![]() ${\cal X}$
. The symbol
${\cal X}$
. The symbol
![]() $E_B$
denotes the exceptional divisors of the blow-up of B on
$E_B$
denotes the exceptional divisors of the blow-up of B on
![]() ${\cal Y}$
. Since outside
${\cal Y}$
. Since outside
![]() $E_B$
the varieties
$E_B$
the varieties
![]() ${\cal X}_B$
and
${\cal X}_B$
and
![]() ${\cal X}$
are isomorphic, it is sufficient to show that every point
${\cal X}$
are isomorphic, it is sufficient to show that every point
![]() $p\in {\cal X}_B\cap E_B$
is either non-singular or a multi-quadratic singularity of the variety
$p\in {\cal X}_B\cap E_B$
is either non-singular or a multi-quadratic singularity of the variety
![]() $U_B$
of type
$U_B$
of type
![]() $2^l$
, where
$2^l$
, where
![]() $l\geqslant 1$
, and of rank
$l\geqslant 1$
, and of rank
![]() $\geqslant r_l$
. We assume that the point p lies over the point
$\geqslant r_l$
. We assume that the point p lies over the point
![]() $o\in U$
and is a singularity of the variety
$o\in U$
and is a singularity of the variety
![]() $U_B$
.
$U_B$
.
By a linear change of local parameters
![]() $u_1,\dots ,u_m$
, we may ensure that at the point
$u_1,\dots ,u_m$
, we may ensure that at the point
![]() $p\in {\cal Y}_B$
, there is a system of local parameters
$p\in {\cal Y}_B$
, there is a system of local parameters
linked to the original system of parameters
![]() $u_*$
by the standard relations
$u_*$
by the standard relations
The local equation of the exceptional divisor
![]() $E_B$
at the point p is
$E_B$
at the point p is
![]() $v_1=0$
, and the subvariety
$v_1=0$
, and the subvariety
![]() ${\cal X}_B\subset {\cal Y}_B$
at that point is defined by the equations
${\cal X}_B\subset {\cal Y}_B$
at that point is defined by the equations
Write down
![]() $\widetilde {\beta }_i=\widetilde {\beta }_{i,1} +\widetilde {\beta }_{1,2}+\dots $
and assume that for some
$\widetilde {\beta }_i=\widetilde {\beta }_{i,1} +\widetilde {\beta }_{1,2}+\dots $
and assume that for some
![]() $l\in \{1,\dots ,k\}$
, the linear forms
$l\in \{1,\dots ,k\}$
, the linear forms
![]() $\widetilde {\beta }_{j,1}$
,
$\widetilde {\beta }_{j,1}$
,
![]() $l+1\leqslant j\leqslant k$
are linearly independent, and moreover,
$l+1\leqslant j\leqslant k$
are linearly independent, and moreover,
so that there are relations
 $$ \begin{align*}\widetilde{\beta}_{i,1}=\sum^k_{j=l+1}a_{i,j}\widetilde{\beta}_{i,1}, \end{align*} $$
$$ \begin{align*}\widetilde{\beta}_{i,1}=\sum^k_{j=l+1}a_{i,j}\widetilde{\beta}_{i,1}, \end{align*} $$
![]() $i=1,\dots ,l$
. Replacing the original system of local equations
$i=1,\dots ,l$
. Replacing the original system of local equations
![]() $\beta _1,\dots ,\beta _k$
by
$\beta _1,\dots ,\beta _k$
by
 $$ \begin{align*}\beta_i-\sum^k_{j=l+1}a_{i,j}\beta_j,\,\,i=1,\dots,l,\quad \beta_{l+1},\dots,\beta_k, \end{align*} $$
$$ \begin{align*}\beta_i-\sum^k_{j=l+1}a_{i,j}\beta_j,\,\,i=1,\dots,l,\quad \beta_{l+1},\dots,\beta_k, \end{align*} $$
we may assume that the linear forms
![]() $\widetilde {\beta }_{i,1}$
,
$\widetilde {\beta }_{i,1}$
,
![]() $i=1,\dots ,l$
are identically zero. In that case, the following claim is true.
$i=1,\dots ,l$
are identically zero. In that case, the following claim is true.
Lemma 4.1. For
![]() $i=1,\dots ,l$
the quadratic forms
$i=1,\dots ,l$
the quadratic forms
![]() $\overline {\beta }_{i,2}$
depend only on
$\overline {\beta }_{i,2}$
depend only on
![]() $u_2,\dots ,u_m$
and
$u_2,\dots ,u_m$
and
where every monomial in the quadratic form
![]() $\beta ^{\sharp }_{i,2}$
is divisible either by
$\beta ^{\sharp }_{i,2}$
is divisible either by
![]() $v_1$
, or by
$v_1$
, or by
![]() $u_i$
,
$u_i$
,
![]() $m+1\leqslant i\leqslant N$
.
$m+1\leqslant i\leqslant N$
.
Proof. This is obvious because every monomial in
![]() $\overline {\beta }_{i,j}$
is divisible by some quadratic monomial in
$\overline {\beta }_{i,j}$
is divisible by some quadratic monomial in
![]() $u_1,\dots ,u_m$
, and
$u_1,\dots ,u_m$
, and
![]() $\widetilde {\beta }_{i,1}\equiv 0$
for
$\widetilde {\beta }_{i,1}\equiv 0$
for
![]() $i=1,\dots ,l$
, and by the standard formulas, transforming regular functions under a blow-up. Q.E.D. for the lemma.
$i=1,\dots ,l$
, and by the standard formulas, transforming regular functions under a blow-up. Q.E.D. for the lemma.
The lemma gives us the inequality
Setting
![]() $T_p{\cal X}_B=\{\widetilde {\beta }_{i,1}=0\,|\, l+1\leqslant j\leqslant k\}$
and using Remark 1.4, we get
$T_p{\cal X}_B=\{\widetilde {\beta }_{i,1}=0\,|\, l+1\leqslant j\leqslant k\}$
and using Remark 1.4, we get
Therefore,
![]() $p\in {\cal X}_B$
is a multi-quadratic singularity of type
$p\in {\cal X}_B$
is a multi-quadratic singularity of type
![]() $2^l$
and rank
$2^l$
and rank
![]() $\geqslant r_l$
. Q.E.D. for Theorem 4.1.
$\geqslant r_l$
. Q.E.D. for Theorem 4.1.
Corollary 4.2. Assume that
![]() $\cal X$
has multi-quadratic singularities of type
$\cal X$
has multi-quadratic singularities of type
![]() $\underline {r}$
, where
$\underline {r}$
, where
![]() $r_l\geqslant 3l+1$
for all
$r_l\geqslant 3l+1$
for all
![]() $l=1,\dots ,k$
. Then the singularities of
$l=1,\dots ,k$
. Then the singularities of
![]() ${\cal X}$
are terminal.
${\cal X}$
are terminal.
Proof. In the notations of the proof of Theorem 4.1, it is sufficient to show the inequality
Assume that a point
![]() $o\in B$
of general position is a multi-quadratic singularity of type
$o\in B$
of general position is a multi-quadratic singularity of type
![]() $2^l$
. From the claim (ii) of Corollary 4.1, we get the inequality
$2^l$
. From the claim (ii) of Corollary 4.1, we get the inequality
so that
![]() $\mathop {\mathrm {codim}}(B\subset {\cal Y})\geqslant k+l+2$
, and for that reason,
$\mathop {\mathrm {codim}}(B\subset {\cal Y})\geqslant k+l+2$
, and for that reason,
By the adjunction formula,
which implies the required inequality. Q.E.D. for the corollary.
This completes the proof of Theorem 1.1.
4.4 Singularities of complete intersections
Let us show Proposition 4.2. We will prove the claims (i) and (ii) simultaneously: by Grothendieck’s theorem on parafactoriality [Reference Call and Lyubeznik21, Reference Call25], the claim (ii) for
![]() $e=4$
implies the factoriality of the variety Q.
$e=4$
implies the factoriality of the variety Q.
We argue by induction on
![]() $l\geqslant 1$
. For one quadric (
$l\geqslant 1$
. For one quadric (
![]() $l=1$
), the claims (i) and (ii) are obvious. Since
$l=1$
), the claims (i) and (ii) are obvious. Since
we may assume that the claims (i) and (ii) are true for the tuple of quadratic forms
![]() $q_1$
, …,
$q_1$
, …,
![]() $q_{l-1}$
. In particular, the scheme of their common zeros
$q_{l-1}$
. In particular, the scheme of their common zeros
![]() $Q_{l-1}$
is an irreducible reduced factorial complete intersection of type
$Q_{l-1}$
is an irreducible reduced factorial complete intersection of type
![]() $2^{l-1}$
in
$2^{l-1}$
in
![]() ${\mathbb P}^{N-1}$
, so that
${\mathbb P}^{N-1}$
, so that
![]() $\mathop {\mathrm {Pic}} Q_{l-1}={\mathbb Z} H_{l-1}$
, where
$\mathop {\mathrm {Pic}} Q_{l-1}={\mathbb Z} H_{l-1}$
, where
![]() $H_{l-1}$
is the class of a hyperplane section: every effective divisor on
$H_{l-1}$
is the class of a hyperplane section: every effective divisor on
![]() $Q_{l-1}$
is cut out on
$Q_{l-1}$
is cut out on
![]() $Q_{l-1}$
by a hypersurface in
$Q_{l-1}$
by a hypersurface in
![]() ${\mathbb P}^{N-1}$
.
${\mathbb P}^{N-1}$
.
The scheme of common zeros of the quadratic forms
![]() $q_1$
, …,
$q_1$
, …,
![]() $q_l$
is the divisor of zeros of the form
$q_l$
is the divisor of zeros of the form
![]() $q_l$
on the variety
$q_l$
on the variety
![]() $Q_{l-1}$
. This divisor is reducible or non-reduced if and only if there is a form
$Q_{l-1}$
. This divisor is reducible or non-reduced if and only if there is a form
![]() $q^*_l$
of rank
$q^*_l$
of rank
![]() $\leqslant 2$
such that
$\leqslant 2$
such that
and in that case,
![]() $\mathop {\mathrm {rk}}q_{[1,l]}\leqslant 2$
, which contradicts the assumption. Therefore, Q is an irreducible reduced complete intersection. It is easy to see that
$\mathop {\mathrm {rk}}q_{[1,l]}\leqslant 2$
, which contradicts the assumption. Therefore, Q is an irreducible reduced complete intersection. It is easy to see that
![]() $Q\subset {\mathbb P}^{N-1}$
is non-degenerate. Since
$Q\subset {\mathbb P}^{N-1}$
is non-degenerate. Since
(for the claim (i) we set
![]() $e=4$
), we have
$e=4$
), we have
so that
It is easy to see that a point
![]() $p\in Q$
, which is non-singular on
$p\in Q$
, which is non-singular on
![]() $Q_{l-1}$
, is singular on Q if and only if for some
$Q_{l-1}$
, is singular on Q if and only if for some
![]() $\lambda _1,\dots ,\lambda _{l-1}$
, the quadric
$\lambda _1,\dots ,\lambda _{l-1}$
, the quadric
is singular at that point. Since the singular set of a quadric of rank r in
![]() ${\mathbb P}^{N-1}$
has dimension
${\mathbb P}^{N-1}$
has dimension
![]() $N-1-r$
, we conclude that the dimension of the set
$N-1-r$
, we conclude that the dimension of the set
does not exceed
![]() $N-1-\mathop {\mathrm {rk}}q_{[1,l]}+(l-1)$
, whence it follows that the codimension of that set with respect to Q is at least
$N-1-\mathop {\mathrm {rk}}q_{[1,l]}+(l-1)$
, whence it follows that the codimension of that set with respect to Q is at least
![]() $\mathop {\mathrm {rk}}q_{[1,l]}-2l+1\geqslant e$
. Q.E.D. for Proposition 4.2.
$\mathop {\mathrm {rk}}q_{[1,l]}-2l+1\geqslant e$
. Q.E.D. for Proposition 4.2.
4.5 Linear subspaces and projections
Now let us consider the questions that are naturally close to Proposition 4.2 and its proof. These questions are of key importance in the proof of Theorem 3.3 (which will be given in §5). Since in Theorem 3.3 the multi-quadratic singularity is of type
![]() $2^k$
, starting from this moment, we consider k quadratic forms
$2^k$
, starting from this moment, we consider k quadratic forms
![]() $q_1$
, …,
$q_1$
, …,
![]() $q_k$
in N variables (that is, on
$q_k$
in N variables (that is, on
![]() ${\mathbb P}^{N-1}$
), and the tuple of them is denoted by the symbol
${\mathbb P}^{N-1}$
), and the tuple of them is denoted by the symbol
![]() $q_{[1,k]}$
. The symbol Q, as above, stands for the complete intersection of these k quadrics
$q_{[1,k]}$
. The symbol Q, as above, stands for the complete intersection of these k quadrics
![]() $\{q_i=0\}$
in
$\{q_i=0\}$
in
![]() ${\mathbb P}^{N-1}$
.
${\mathbb P}^{N-1}$
.
Proposition 4.3. Assume that for some
![]() $b\geqslant 0$
, the inequality
$b\geqslant 0$
, the inequality
holds. Then for every point
![]() $p\in Q\setminus \mathop {\mathrm {Sing}} Q$
, there is a linear space
$p\in Q\setminus \mathop {\mathrm {Sing}} Q$
, there is a linear space
![]() $\Pi \subset {\mathbb P}^{N-1}$
of dimension b, such that
$\Pi \subset {\mathbb P}^{N-1}$
of dimension b, such that
![]() $p\in \Pi \subset Q$
, and moreover,
$p\in \Pi \subset Q$
, and moreover,
![]() $\Pi \cap \mathop {\mathrm {Sing}} Q=\emptyset $
.
$\Pi \cap \mathop {\mathrm {Sing}} Q=\emptyset $
.
Proof contains the (obvious) construction of such linear subspaces. We argue by induction on b. If
![]() $b=0$
, then
$b=0$
, then
![]() $\Pi $
is the point p itself and there is nothing to prove. Assume that
$\Pi $
is the point p itself and there is nothing to prove. Assume that
![]() $b\geqslant 1$
and for
$b\geqslant 1$
and for
![]() $b-1$
the claim of the Proposition is true.
$b-1$
the claim of the Proposition is true.
Consider the linear subspace
![]() $T=T_pQ$
of codimension k in
$T=T_pQ$
of codimension k in
![]() ${\mathbb P}^{N-1}$
. Obviously, every linear space in
${\mathbb P}^{N-1}$
. Obviously, every linear space in
![]() ${\mathbb P}^{N-1}$
that contains the point p and is contained in Q is contained in T, too. Furthermore,
${\mathbb P}^{N-1}$
that contains the point p and is contained in Q is contained in T, too. Furthermore,
![]() $Q\cap T$
is defined by the quadratic forms
$Q\cap T$
is defined by the quadratic forms
![]() $q_1|_T,\dots ,q_k|_T$
. Since
$q_1|_T,\dots ,q_k|_T$
. Since
![]() $\mathop {\mathrm {rk}} q_{[1,k]}|_T\geqslant \mathop {\mathrm {rk}} q_{[1,k]}-2k$
, the inequality
$\mathop {\mathrm {rk}} q_{[1,k]}|_T\geqslant \mathop {\mathrm {rk}} q_{[1,k]}-2k$
, the inequality
holds, where every quadric
![]() $\{q_i|_T=0\}$
,
$\{q_i|_T=0\}$
,
![]() $i=1,\dots ,k$
, is by construction a cone with the vertex at p. Therefore,
$i=1,\dots ,k$
, is by construction a cone with the vertex at p. Therefore,
![]() $Q\cap T$
is a cone with the vertex at the point p. Let
$Q\cap T$
is a cone with the vertex at the point p. Let
![]() $P\subset T$
be a hyperplane in T that does not contain the point p. Then the cone
$P\subset T$
be a hyperplane in T that does not contain the point p. Then the cone
![]() $Q\cap T$
is a cone with the base
$Q\cap T$
is a cone with the base
![]() $Q\cap P$
, where
$Q\cap P$
, where
![]() $Q\cap P$
is a complete intersection of the quadrics
$Q\cap P$
is a complete intersection of the quadrics
![]() $\{q_i|_P=0\}$
, where, obviously,
$\{q_i|_P=0\}$
, where, obviously,
By the induction hypothesis, there is a linear subspace
![]() $\Pi ^{\sharp }\subset P$
of dimension
$\Pi ^{\sharp }\subset P$
of dimension
![]() $(b-1)$
, such that
$(b-1)$
, such that
![]() $\Pi ^{\sharp }\subset Q\cap P$
and
$\Pi ^{\sharp }\subset Q\cap P$
and
![]() $\Pi ^{\sharp }\cap \mathop {\mathrm {Sing}}(Q\cap P)=\emptyset $
.
$\Pi ^{\sharp }\cap \mathop {\mathrm {Sing}}(Q\cap P)=\emptyset $
.
Furthermore, the set of singular points
![]() $\mathop {\mathrm {Sing}}(Q\cap T)$
is a cone with the vertex p, the base of which is
$\mathop {\mathrm {Sing}}(Q\cap T)$
is a cone with the vertex p, the base of which is
![]() $\mathop {\mathrm {Sing}}(Q\cap P)$
, so that for the subspace
$\mathop {\mathrm {Sing}}(Q\cap P)$
, so that for the subspace
![]() $\Pi =\langle p,\Pi ^{\sharp }\rangle $
, which is a cone with the vertex p and the base
$\Pi =\langle p,\Pi ^{\sharp }\rangle $
, which is a cone with the vertex p and the base
![]() $\Pi ^{\sharp }$
, we have
$\Pi ^{\sharp }$
, we have
![]() $\Pi \cap \mathop {\mathrm {Sing}}(Q\cap T)=\{p\}$
. Since
$\Pi \cap \mathop {\mathrm {Sing}}(Q\cap T)=\{p\}$
. Since
![]() $T\cap \mathop {\mathrm {Sing}}Q\subset \mathop {\mathrm {Sing}}(Q\cap T)$
and
$T\cap \mathop {\mathrm {Sing}}Q\subset \mathop {\mathrm {Sing}}(Q\cap T)$
and
![]() $p\not \in \mathop {\mathrm {Sing}}Q$
, we get
$p\not \in \mathop {\mathrm {Sing}}Q$
, we get
![]() $\Pi \cap \mathop {\mathrm {Sing}}Q=\emptyset $
, which completes the proof of the proposition.
$\Pi \cap \mathop {\mathrm {Sing}}Q=\emptyset $
, which completes the proof of the proposition.
Proposition 4.4. Let
![]() $b\geqslant \beta \geqslant 0$
be some integers. Assume that the inequality
$b\geqslant \beta \geqslant 0$
be some integers. Assume that the inequality
holds. Then for every linear subspace
![]() $P\subset {\mathbb P}^{N-1}$
of codimension
$P\subset {\mathbb P}^{N-1}$
of codimension
![]() $\beta $
and a general linear subspace
$\beta $
and a general linear subspace
![]() $\Pi \subset Q$
,
$\Pi \subset Q$
,
![]() $\Pi \cap \mathop {\mathrm {Sing}}=\emptyset $
, of dimension b, the intersection
$\Pi \cap \mathop {\mathrm {Sing}}=\emptyset $
, of dimension b, the intersection
![]() $P\cap \Pi $
has codimension
$P\cap \Pi $
has codimension
![]() $\beta $
in
$\beta $
in
![]() $\Pi $
.
$\Pi $
.
Proof. Again, we argue by induction on
![]() $\beta $
; the case
$\beta $
; the case
![]() $\beta =0$
is trivial. Only the equality
$\beta =0$
is trivial. Only the equality
![]() $\Pi \cap \mathop {\mathrm {Sing}} Q=\emptyset $
for a general subspace
$\Pi \cap \mathop {\mathrm {Sing}} Q=\emptyset $
for a general subspace
![]() $\Pi \subset Q$
of dimension
$\Pi \subset Q$
of dimension
![]() $b \geqslant 0$
is needed, and it is true by Proposition 4.3.
$b \geqslant 0$
is needed, and it is true by Proposition 4.3.
Let us show our claim in the assumption that it is true for
![]() $\beta -1$
.
$\beta -1$
.
First of all, note that
so that by Proposition 4.2, the intersection
![]() $Q\cap P$
is an irreducible reduced complete intersection of type
$Q\cap P$
is an irreducible reduced complete intersection of type
![]() $2^k$
in P; in particular, a point of general position
$2^k$
in P; in particular, a point of general position
![]() $p\in Q\cap P$
is non-singular. This means that
$p\in Q\cap P$
is non-singular. This means that
is of codimension k in P, so that
![]() $T_pQ$
and P are in general position. The property to be in general position is an open property; therefore, for a point of general position
$T_pQ$
and P are in general position. The property to be in general position is an open property; therefore, for a point of general position
![]() $p\in Q$
(in particular,
$p\in Q$
(in particular,
![]() $p\not \in P$
), the linear subspaces
$p\not \in P$
), the linear subspaces
![]() $T_pQ$
and P are in general position and their intersection
$T_pQ$
and P are in general position and their intersection
![]() $T_pQ\cap P$
is of codimension k in P and of codimension
$T_pQ\cap P$
is of codimension k in P and of codimension
![]() $\beta $
in
$\beta $
in
![]() $T_pQ$
.
$T_pQ$
.
Consider a general hypersurface Z in
![]() $T_pQ$
, containing the subspace
$T_pQ$
, containing the subspace
![]() $T_pQ\cap P$
and not containing the point p. We have
$T_pQ\cap P$
and not containing the point p. We have
so that by the induction hypothesis for a general linear subspace
![]() $\Pi ^{\sharp }\subset Q\cap Z$
of dimension
$\Pi ^{\sharp }\subset Q\cap Z$
of dimension
![]() $(b-1)$
that does not meet the set
$(b-1)$
that does not meet the set
![]() $\mathop {\mathrm {Sing}}(Q\cap Z)$
, the intersection
$\mathop {\mathrm {Sing}}(Q\cap Z)$
, the intersection
is of codimension
![]() $\beta -1=\mathop {\mathrm {codim}}((P\cap T_pQ)\subset Z)$
with respect to
$\beta -1=\mathop {\mathrm {codim}}((P\cap T_pQ)\subset Z)$
with respect to
![]() $\Pi ^{\sharp }$
.
$\Pi ^{\sharp }$
.
Then the linear space
of dimension b is contained in Q and does not meet the set
![]() $\mathop {\mathrm {Sing}}Q$
(see the proof of Proposition 4.3), and finally, the subspace
$\mathop {\mathrm {Sing}}Q$
(see the proof of Proposition 4.3), and finally, the subspace
is of codimension
![]() $\beta $
with respect to
$\beta $
with respect to
![]() $\Pi $
. Q.E.D. for the proposition.
$\Pi $
. Q.E.D. for the proposition.
Corollary 4.3. In the assumptions of Proposition 4.4, where
![]() $\beta \geqslant k$
, let
$\beta \geqslant k$
, let
![]() $Y\subset Q$
be an irreducible subvariety of codimension
$Y\subset Q$
be an irreducible subvariety of codimension
![]() $\beta -k$
. Then the restriction onto Y of the projection
$\beta -k$
. Then the restriction onto Y of the projection
from a general subspace
![]() $\Pi \subset Q$
of dimension b is dominant.
$\Pi \subset Q$
of dimension b is dominant.
Proof. Let
![]() $p\in Y$
be a non-singular point. We apply Proposition 4.4 to the subspace
$p\in Y$
be a non-singular point. We apply Proposition 4.4 to the subspace
![]() $P=T_pY\subset {\mathbb P^{N-1}}$
of codimension
$P=T_pY\subset {\mathbb P^{N-1}}$
of codimension
![]() $\beta $
. A general subspace
$\beta $
. A general subspace
![]() $\Pi \subset Q$
of dimension
$\Pi \subset Q$
of dimension
![]() $b\geqslant \beta $
does not contain the point p and is in general position with P, so that
$b\geqslant \beta $
does not contain the point p and is in general position with P, so that
![]() $\mathop {\mathrm {pr}}_{\Pi }|_P$
is regular in a neighborhood of the point p and its differential at the point p is an epimorphism. Therefore,
$\mathop {\mathrm {pr}}_{\Pi }|_P$
is regular in a neighborhood of the point p and its differential at the point p is an epimorphism. Therefore,
![]() $\mathop {\mathrm {pr}}_{\Pi }|_Y$
is regular at the point p, and its differential at that point is an epimorphism. Q.E.D. for the corollary.
$\mathop {\mathrm {pr}}_{\Pi }|_Y$
is regular at the point p, and its differential at that point is an epimorphism. Q.E.D. for the corollary.
Note an important particular case.
Corollary 4.4. Assume that
![]() $b\geqslant k$
and the inequality
$b\geqslant k$
and the inequality
holds. Then the restriction of the projection
![]() $\mathop {\mathrm {pr}}_{\Pi }$
from a general subspace
$\mathop {\mathrm {pr}}_{\Pi }$
from a general subspace
![]() $\Pi \subset Q$
of dimension b onto Q is dominant, and its general fibre is a linear subspace of dimension
$\Pi \subset Q$
of dimension b onto Q is dominant, and its general fibre is a linear subspace of dimension
![]() $b+1-k$
.
$b+1-k$
.
Proof. That it is dominant follows from the previous corollary, so that the dimension of a general fibre is
![]() $b+1-k$
. Furthermore,
$b+1-k$
. Furthermore,
![]() $\mathop {\mathrm {pr}}_{\Pi }$
fibres
$\mathop {\mathrm {pr}}_{\Pi }$
fibres
![]() ${\mathbb P}^{N-1}$
(more precisely,
${\mathbb P}^{N-1}$
(more precisely,
![]() ${\mathbb P}^{N-1}\setminus \Pi $
) into linear subspaces
${\mathbb P}^{N-1}\setminus \Pi $
) into linear subspaces
![]() $\Pi ^{\sharp }\supset \Pi $
of dimension
$\Pi ^{\sharp }\supset \Pi $
of dimension
![]() $b+1$
. The centre
$b+1$
. The centre
![]() $\Pi $
of the projection is a hyperplane in
$\Pi $
of the projection is a hyperplane in
![]() $\Pi ^{\sharp }$
. Since
$\Pi ^{\sharp }$
. Since
![]() $\Pi \subset Q$
, the quadric
$\Pi \subset Q$
, the quadric
![]() $\{q_i|_{\Pi ^{\sharp }}=0\}$
is the union of two hyperplanes, one of which is
$\{q_i|_{\Pi ^{\sharp }}=0\}$
is the union of two hyperplanes, one of which is
![]() $\Pi $
. Now the claim of the corollary is obvious.
$\Pi $
. Now the claim of the corollary is obvious.
Let
![]() $\Pi \subset Q$
be a linear subspace of dimension
$\Pi \subset Q$
be a linear subspace of dimension
![]() $b\geqslant k$
, not meeting the set
$b\geqslant k$
, not meeting the set
![]() $\mathop {\mathrm {Sing}}Q$
, and
$\mathop {\mathrm {Sing}}Q$
, and
![]() $\sigma \colon \widetilde {Q}\to Q$
and
$\sigma \colon \widetilde {Q}\to Q$
and
![]() $\sigma _{\mathbb P}\colon \widetilde {{\mathbb P}^{N-1}}\to {\mathbb P}^{N-1}$
the blow-ups of
$\sigma _{\mathbb P}\colon \widetilde {{\mathbb P}^{N-1}}\to {\mathbb P}^{N-1}$
the blow-ups of
![]() $\Pi $
on Q and
$\Pi $
on Q and
![]() ${\mathbb P}^{N-1}$
, respectively, so that we can identify
${\mathbb P}^{N-1}$
, respectively, so that we can identify
![]() $\widetilde {Q}$
with the strict transform of Q on
$\widetilde {Q}$
with the strict transform of Q on
![]() $\widetilde {{\mathbb P}^{N-1}}$
. By the symbols
$\widetilde {{\mathbb P}^{N-1}}$
. By the symbols
![]() $E_Q$
and
$E_Q$
and
![]() $E_{\mathbb P}$
we denote the exceptional divisors of these blow ups; we consider
$E_{\mathbb P}$
we denote the exceptional divisors of these blow ups; we consider
![]() $E_Q$
as a subvariety in
$E_Q$
as a subvariety in
![]() $E_{\mathbb P}$
. Let
$E_{\mathbb P}$
. Let
![]() $\varphi \colon \widetilde {Q}\to {\mathbb P}^{N-b-2}$
and
$\varphi \colon \widetilde {Q}\to {\mathbb P}^{N-b-2}$
and
![]() $\varphi _{\mathbb P}\colon \widetilde {{\mathbb P}^{N-1}} \to {\mathbb P}^{N-b-2}$
be the regularizations of the rational maps
$\varphi _{\mathbb P}\colon \widetilde {{\mathbb P}^{N-1}} \to {\mathbb P}^{N-b-2}$
be the regularizations of the rational maps
![]() $\mathop {\mathrm {pr}}_{\Pi }|_Q$
and
$\mathop {\mathrm {pr}}_{\Pi }|_Q$
and
![]() $\mathop {\mathrm {pr}}_{\Pi }$
, respectively. We have the natural identification
$\mathop {\mathrm {pr}}_{\Pi }$
, respectively. We have the natural identification
![]() $E_{\mathbb P}=\Pi \times {\mathbb P}^{N-b-2}$
, where the map
$E_{\mathbb P}=\Pi \times {\mathbb P}^{N-b-2}$
, where the map
is the projection onto the second factor. In the assumptions of Corollary 4.4, the morphism
![]() $\varphi $
is surjective, and for a point of general position
$\varphi $
is surjective, and for a point of general position
![]() $p\in {\mathbb P}^{N-b-2}$
, the fibre
$p\in {\mathbb P}^{N-b-2}$
, the fibre
![]() $\varphi ^{-1}(p)$
is a linear subspace of dimension
$\varphi ^{-1}(p)$
is a linear subspace of dimension
![]() $b+1-k$
in
$b+1-k$
in
![]() $\varphi ^{-1}_{\mathbb P}(p)\cong {\mathbb P}^{b+1}$
, which is not contained entirely in the hyperplane
$\varphi ^{-1}_{\mathbb P}(p)\cong {\mathbb P}^{b+1}$
, which is not contained entirely in the hyperplane
which identifies naturally with
![]() $\Pi $
, and for that reason,
$\Pi $
, and for that reason,
![]() $\varphi ^{-1}(p)\cap E_{\mathbb P}$
identifies naturally with a subspace of dimension
$\varphi ^{-1}(p)\cap E_{\mathbb P}$
identifies naturally with a subspace of dimension
![]() $b-k$
in
$b-k$
in
![]() $\Pi $
(and a hyperplane in
$\Pi $
(and a hyperplane in
![]() $\varphi ^{-1}(p)$
). However,
$\varphi ^{-1}(p)$
). However,
so that arguing by dimensions, we conclude that the restriction
![]() $\varphi |_{E_Q}$
is surjective.
$\varphi |_{E_Q}$
is surjective.
Proposition 4.5. In the assumptions of Corollary 4.4, let
![]() $Y\subset \Pi $
be an irreducible closed subset, and assume that
$Y\subset \Pi $
be an irreducible closed subset, and assume that
Then the restriction
![]() $\varphi |_{\sigma ^{-1}(Y)}$
is surjective, so that for a point of general position
$\varphi |_{\sigma ^{-1}(Y)}$
is surjective, so that for a point of general position
![]() $p\in {\mathbb P}^{N-b-2}$
, the intersection
$p\in {\mathbb P}^{N-b-2}$
, the intersection
![]() $\varphi ^{-1}(p)\cap \sigma ^{-1}(Y)$
is nonempty and each of its components is of codimension
$\varphi ^{-1}(p)\cap \sigma ^{-1}(Y)$
is nonempty and each of its components is of codimension
![]() $\mathop {\mathrm {codim}} (Y\subset \Pi )$
in the projective space
$\mathop {\mathrm {codim}} (Y\subset \Pi )$
in the projective space
![]() $\varphi ^{-1}(p)\cap E_{\mathbb P}$
.
$\varphi ^{-1}(p)\cap E_{\mathbb P}$
.
Proof. Obviously,
Since
![]() $\varphi ^{-1}(p)\subset \widetilde {Q}$
, the equality
$\varphi ^{-1}(p)\subset \widetilde {Q}$
, the equality
holds, but
![]() $\sigma ^{-1}(Y)=Y\times {\mathbb P}^{N-b-2}$
in terms of the direct decomposition of the exceptional divisor
$\sigma ^{-1}(Y)=Y\times {\mathbb P}^{N-b-2}$
in terms of the direct decomposition of the exceptional divisor
![]() $E_{\mathbb P}$
. Therefore, identifying the fibre of the projection
$E_{\mathbb P}$
. Therefore, identifying the fibre of the projection
![]() $\varphi _{\mathbb P}|_{E_{\mathbb P}}$
with the projective space
$\varphi _{\mathbb P}|_{E_{\mathbb P}}$
with the projective space
![]() $\Pi $
, we get that the intersection
$\Pi $
, we get that the intersection
![]() $\varphi ^{-1}(p)\cap \sigma ^{-1}(Y)$
identifies naturally with the intersection of Y and the linear subspace
$\varphi ^{-1}(p)\cap \sigma ^{-1}(Y)$
identifies naturally with the intersection of Y and the linear subspace
![]() $\varphi ^{-1}(p)\cap E_{\mathbb P}$
of dimension
$\varphi ^{-1}(p)\cap E_{\mathbb P}$
of dimension
![]() $b-k$
in
$b-k$
in
![]() $\Pi $
. By our assumption, this intersection is nonempty, so that the morphism
$\Pi $
. By our assumption, this intersection is nonempty, so that the morphism
![]() $\varphi |_{\sigma ^{-1}(Y)}$
is surjective. Q.E.D. for the proposition.
$\varphi |_{\sigma ^{-1}(Y)}$
is surjective. Q.E.D. for the proposition.
5 The special hyperplane section
In this section, we prove Theorem 3.3.
5.1 Start of the proof
We use the notations of Subsection 1.7 and the assumptions of Theorem 3.3. Recall that
is the set of admissible dimensions for the working triple
![]() $(X,D,o)$
. Consider a general subspace
$(X,D,o)$
. Consider a general subspace
![]() $P\ni o$
in
$P\ni o$
in
![]() ${\mathbb P}(X)$
of the minimal admissible dimension
${\mathbb P}(X)$
of the minimal admissible dimension
![]() $2k+3$
. Since
$2k+3$
. Since
![]() $a(E_{X\cap P})=2$
and
$a(E_{X\cap P})=2$
and
![]() $\nu (D)\leqslant \frac 32n(D)<2n(D)$
, we conclude that the pair
$\nu (D)\leqslant \frac 32n(D)<2n(D)$
, we conclude that the pair
 $$ \begin{align*}\left((X\cap P)^+,\frac{1}{n(D)} D|^+_{X\cap P}\right) \end{align*} $$
$$ \begin{align*}\left((X\cap P)^+,\frac{1}{n(D)} D|^+_{X\cap P}\right) \end{align*} $$
is not log-canonical, but canonical outside the exceptional divisor
![]() $E_{X\cap P}$
. By the inequality
$E_{X\cap P}$
. By the inequality
![]() ${\nu (D)<2n(D)}$
, we can apply the connectedness principle to this pair:
${\nu (D)<2n(D)}$
, we can apply the connectedness principle to this pair:
 $$ \begin{align} \mathop{\mathrm{LCS}}\ \left((X\cap P)^+,\frac{1}{n(D)}D|^+_{X\cap P}\right) \end{align} $$
$$ \begin{align} \mathop{\mathrm{LCS}}\ \left((X\cap P)^+,\frac{1}{n(D)}D|^+_{X\cap P}\right) \end{align} $$
is a proper connected closed subset of the exceptional divisor
![]() $E_{X\cap P}$
. There are the following options:
$E_{X\cap P}$
. There are the following options:
![]() $(1)_P$
this subset contains a divisor,
$(1)_P$
this subset contains a divisor,
![]() $(2)_P$
some irreducible component of maximal dimension
$(2)_P$
some irreducible component of maximal dimension
![]() $B(P)\subset E_{X\cap P}$
in this set has a positive dimension and codimension
$B(P)\subset E_{X\cap P}$
in this set has a positive dimension and codimension
![]() $\geqslant 2$
in
$\geqslant 2$
in
![]() $E_{X\cap P}$
,
$E_{X\cap P}$
,
![]() $(3)_P$
this subset is a point.
$(3)_P$
this subset is a point.
Remark 5.1. In the case
![]() $(1)_P$
, the divisor in the subset (17) is unique and is a hyperplane section of the variety
$(1)_P$
, the divisor in the subset (17) is unique and is a hyperplane section of the variety
![]() $E_{X\cap P}\subset {\mathbb E}_{X\cap P}$
, since
$E_{X\cap P}\subset {\mathbb E}_{X\cap P}$
, since
![]() $D|^+_{X\cap P}$
has along this subvariety the multiplicity
$D|^+_{X\cap P}$
has along this subvariety the multiplicity
![]() $>n(D)$
(since it is the centre of some non-log-canonical singularity), whereas the restriction
$>n(D)$
(since it is the centre of some non-log-canonical singularity), whereas the restriction
![]() $D^+|_{E_{X\cap P}}$
is cut out on
$D^+|_{E_{X\cap P}}$
is cut out on
![]() $E_{X\cap P}$
by a hypersurface of degree
$E_{X\cap P}$
by a hypersurface of degree
![]() $\nu (D)<2n(D)$
.
$\nu (D)<2n(D)$
.
Since
![]() $P\ni o$
is a subspace of general position, we go back to the original variety X and get that the pair
$P\ni o$
is a subspace of general position, we go back to the original variety X and get that the pair
![]() $(X^+,\frac {1}{n(D)}D|^+)$
is not log-canonical, and moreover, for the centre
$(X^+,\frac {1}{n(D)}D|^+)$
is not log-canonical, and moreover, for the centre
![]() $B\subset E_X$
of some non-log-canonical singularity of that pair, one of the three option takes place:
$B\subset E_X$
of some non-log-canonical singularity of that pair, one of the three option takes place:
(1) B is a hyperplane section of
![]() $E_X\subset {\mathbb E}_X$
,
$E_X\subset {\mathbb E}_X$
,
(2)
![]() $\mathop {\mathrm {codim}}(B\subset E_X)\in \{2,\dots ,k+1\}$
,
$\mathop {\mathrm {codim}}(B\subset E_X)\in \{2,\dots ,k+1\}$
,
(3) B is a linear subspace of codimension
![]() $2k+2$
in
$2k+2$
in
![]() ${\mathbb E}_X$
, which is contained in
${\mathbb E}_X$
, which is contained in
![]() $E_X$
.
$E_X$
.
Proposition 5.1. The option (1) does not take place.
Proof. Assume the converse: B is a hyperplane section of
![]() $E_X$
. Let
$E_X$
. Let
![]() $R\subset X$
,
$R\subset X$
,
![]() $R\ni o$
be the uniquely determined hyperplane section, such that
$R\ni o$
be the uniquely determined hyperplane section, such that
![]() $R^+\cap E_X=B$
(in other words,
$R^+\cap E_X=B$
(in other words,
![]() ${\mathbb P}(R)^+\cap {\mathbb E}_X$
is the hyperplane in
${\mathbb P}(R)^+\cap {\mathbb E}_X$
is the hyperplane in
![]() ${\mathbb E}_X$
that cuts out B on
${\mathbb E}_X$
that cuts out B on
![]() $E_X$
). Since
$E_X$
). Since
![]() $\mathop {\mathrm {mult}}_BD^+>n(D)$
, we get that for the effective divisor
$\mathop {\mathrm {mult}}_BD^+>n(D)$
, we get that for the effective divisor
![]() $D_R=(D\circ R)$
on R, the inequality
$D_R=(D\circ R)$
on R, the inequality
holds, which is impossible by Theorem 1.4. Q.E.D. for the proposition.
Proposition 5.2. The option (3) does not take place.
Proof. Since
![]() $\mathop {\mathrm {codim}}(B\subset E_X)=k+2$
, this is impossible by the Lefschetz theorem (in order to apply the Lefschetz theorem, it is sufficient to have the inequality
$\mathop {\mathrm {codim}}(B\subset E_X)=k+2$
, this is impossible by the Lefschetz theorem (in order to apply the Lefschetz theorem, it is sufficient to have the inequality
![]() $\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}E_X\subset E_X)\geqslant 2k+6$
, for which by Proposition 4.2 it is sufficient to have the inequality
$\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}E_X\subset E_X)\geqslant 2k+6$
, for which by Proposition 4.2 it is sufficient to have the inequality
![]() $\mathop {\mathrm {rk}}(o\in X)\geqslant 4k+5$
; we have a much stronger condition for the rank of the singularity). Q.E.D. for the proposition.
$\mathop {\mathrm {rk}}(o\in X)\geqslant 4k+5$
; we have a much stronger condition for the rank of the singularity). Q.E.D. for the proposition.
Therefore, the option (2) takes place. By construction (or arguing by dimension),
![]() $B\not \subset \mathop {\mathrm {Sing}}E_X$
. Recall that there is a non-log-canonical singularity of the pair
$B\not \subset \mathop {\mathrm {Sing}}E_X$
. Recall that there is a non-log-canonical singularity of the pair
![]() $(X^+,\frac {1}{n(D)}D^+)$
, the centre of which is B.
$(X^+,\frac {1}{n(D)}D^+)$
, the centre of which is B.
Let
![]() $p\in B$
be a point of general position; in particular,
$p\in B$
be a point of general position; in particular,
![]() $p\not \in \mathop {\mathrm {Sing}}E_X$
and the more so,
$p\not \in \mathop {\mathrm {Sing}}E_X$
and the more so,
![]() $p\not \in \mathop {\mathrm {Sing}} X^+$
. Applying inversion of adjunction in the word for word the same way as in [Reference Pukhlikov20, Chapter 7, Proposition 2.3] (that is, restricting
$p\not \in \mathop {\mathrm {Sing}} X^+$
. Applying inversion of adjunction in the word for word the same way as in [Reference Pukhlikov20, Chapter 7, Proposition 2.3] (that is, restricting
![]() $D^+$
onto a general non-singular surface, containing the point p), we get the alternative: either
$D^+$
onto a general non-singular surface, containing the point p), we get the alternative: either
![]() $\mathop {\mathrm {mult}}_BD^+>2n(D)$
or on the blow-up
$\mathop {\mathrm {mult}}_BD^+>2n(D)$
or on the blow-up
of the point p with the exceptional divisor
![]() $E(p)\subset X^{(p)}$
,
$E(p)\subset X^{(p)}$
,
![]() $E(p)\cong {\mathbb P}^{N(X)-1}$
, there is a hyperplane
$E(p)\cong {\mathbb P}^{N(X)-1}$
, there is a hyperplane
![]() $\Theta (p)\subset E(p)$
in
$\Theta (p)\subset E(p)$
in
![]() $E(p)$
, satisfying the inequality
$E(p)$
, satisfying the inequality
where
![]() $D^{(p)}$
is the strict transform of the divisor
$D^{(p)}$
is the strict transform of the divisor
![]() $D^+$
on
$D^+$
on
![]() $X^{(p)}$
, and moreover, the hyperplane
$X^{(p)}$
, and moreover, the hyperplane
![]() $\Theta (p)$
is uniquely determined by the pair
$\Theta (p)$
is uniquely determined by the pair
![]() $(X^+,\frac {1}{n(D)}D^+)$
and varies algebraically with the point
$(X^+,\frac {1}{n(D)}D^+)$
and varies algebraically with the point
![]() $p\in B$
.
$p\in B$
.
The case when the inequality
![]() $\mathop {\mathrm {mult}}\nolimits _BD^+>2n(D)$
holds is excluded (with simplifications) by the arguments, excluding the option
$\mathop {\mathrm {mult}}\nolimits _BD^+>2n(D)$
holds is excluded (with simplifications) by the arguments, excluding the option
![]() $(2)_{\Theta }$
, given below; see Subsection 5.3, Remark 5.2.
$(2)_{\Theta }$
, given below; see Subsection 5.3, Remark 5.2.
There are two options for the hyperplane
![]() $\Theta (p)$
:
$\Theta (p)$
:
![]() $(1)_{\Theta }$
$(1)_{\Theta }$
![]() $\Theta (p)\neq {\mathbb P}(T_pE_X)$
(where we identify
$\Theta (p)\neq {\mathbb P}(T_pE_X)$
(where we identify
![]() $E(p)$
with the projectivization of the tangent space
$E(p)$
with the projectivization of the tangent space
![]() $T_pX^+$
), so that
$T_pX^+$
), so that
![]() $\Theta (p)$
intersects
$\Theta (p)$
intersects
![]() ${\mathbb P}(T_pE_X)$
by some hyperplane
${\mathbb P}(T_pE_X)$
by some hyperplane
![]() $\Theta _E(p)$
,
$\Theta _E(p)$
,
![]() $(2)_{\Theta }$
the hyperplanes
$(2)_{\Theta }$
the hyperplanes
![]() $\Theta (p)$
and
$\Theta (p)$
and
![]() ${\mathbb P}(T_pE_X)$
in
${\mathbb P}(T_pE_X)$
in
![]() $E(p)$
are equal.
$E(p)$
are equal.
Below (see Subsection 5.3, Remark 5.2), we show that the option
![]() $(2)_{\Theta }$
does not take place: it implies that
$(2)_{\Theta }$
does not take place: it implies that
![]() $E_X\subset D^+$
, which is impossible; the same arguments exclude the inequality
$E_X\subset D^+$
, which is impossible; the same arguments exclude the inequality
![]() $\mathop {\mathrm {mult}}\nolimits _BD^+>2n(D)$
, too.
$\mathop {\mathrm {mult}}\nolimits _BD^+>2n(D)$
, too.
Therefore, we may assume that the option
![]() $(1)_{\Theta }$
takes place.
$(1)_{\Theta }$
takes place.
5.2 The existence of the special hyperplane section
Adding the upper index
![]() $(p)$
means the strict transform on
$(p)$
means the strict transform on
![]() $X^{(p)}$
: we used this principle for the divisor D above and will use it for other subvarieties on
$X^{(p)}$
: we used this principle for the divisor D above and will use it for other subvarieties on
![]() $X^+$
. Our aim is to prove the following claim.
$X^+$
. Our aim is to prove the following claim.
Theorem 5.1. There is a hyperplane section
![]() $\Lambda $
of the exceptional divisor
$\Lambda $
of the exceptional divisor
![]() $E_X\subset {\mathbb E}_X$
, containing B, satisfying the inequality
$E_X\subset {\mathbb E}_X$
, containing B, satisfying the inequality
Moreover, for a point of general position
![]() $p\in B$
, the following equality holds:
$p\in B$
, the following equality holds:
Proof. Let
![]() $L\subset E_X,L\ni p$
be a line in the projective space
$L\subset E_X,L\ni p$
be a line in the projective space
![]() ${\mathbb E}_X$
, such that
${\mathbb E}_X$
, such that
![]() $L\cap \mathop {\mathrm {Sing}}E_X=\emptyset $
and
$L\cap \mathop {\mathrm {Sing}}E_X=\emptyset $
and
Lemma 5.1. The line L is contained in
![]() $D^+$
.
$D^+$
.
Proof. Assume the converse. Then
![]() $D^+|_L$
is an effective divisor on L of degree
$D^+|_L$
is an effective divisor on L of degree
![]() $\nu (D)\leqslant \frac 32n(D)<2n(D)$
. At the same time, the divisor
$\nu (D)\leqslant \frac 32n(D)<2n(D)$
. At the same time, the divisor
![]() $D^+|_L$
contains the point p with multiplicity
$D^+|_L$
contains the point p with multiplicity
![]() $>2n(D)$
due to the inequality (18). The contradiction proves the lemma. Q.E.D.
$>2n(D)$
due to the inequality (18). The contradiction proves the lemma. Q.E.D.
Proposition 5.3. The following inequality holds:
Proof is given in §6.
Let us go back to the proof of Theorem 5.1.
We will construct the set
![]() $\Lambda \subset E_X$
explicitly and then prove that it is a hyperplane section. The exceptional divisor
$\Lambda \subset E_X$
explicitly and then prove that it is a hyperplane section. The exceptional divisor
![]() $E_X$
is a complete intersection of k quadrics in
$E_X$
is a complete intersection of k quadrics in
![]() ${\mathbb E}_X$
:
${\mathbb E}_X$
:
using the notations of Subsection 4.5. Let
![]() $U_B\subset B$
be a nonempty Zariski open subset, where
$U_B\subset B$
be a nonempty Zariski open subset, where
and for every point
![]() $p\in B$
, the option
$p\in B$
, the option
![]() $(1)_{\Theta }$
takes place. By the assumption on the rank of the multi-quadratic point
$(1)_{\Theta }$
takes place. By the assumption on the rank of the multi-quadratic point
![]() $o\in X$
for
$o\in X$
for
![]() $p\in U_{B}$
, the set
$p\in U_{B}$
, the set
![]() $E_X\cap T_pE_X$
(where
$E_X\cap T_pE_X$
(where
![]() $T_pE_X\subset {\mathbb E}_X$
is the embedded tangent space – that is, a linear subspace of codimension k in
$T_pE_X\subset {\mathbb E}_X$
is the embedded tangent space – that is, a linear subspace of codimension k in
![]() ${\mathbb E}_X$
) is irreducible and reduced, and moreover, every hyperplane section of that set is also irreducible and reduced. Indeed, by Proposition 4.2, in order to have these properties, it is sufficient to have the inequality
${\mathbb E}_X$
) is irreducible and reduced, and moreover, every hyperplane section of that set is also irreducible and reduced. Indeed, by Proposition 4.2, in order to have these properties, it is sufficient to have the inequality
![]() $\mathop {\mathrm {rk}}q_{[1,k]}\geqslant 4k+5$
because by Remark 1.4, it implies the inequality
$\mathop {\mathrm {rk}}q_{[1,k]}\geqslant 4k+5$
because by Remark 1.4, it implies the inequality
and we can apply Proposition 4.2. Obviously,
![]() $E_X\cap T_pE_X$
is a cone with the vertex p, consisting of all lines
$E_X\cap T_pE_X$
is a cone with the vertex p, consisting of all lines
![]() $L\subset E_X$
,
$L\subset E_X$
,
![]() $L\ni p$
. The singular set of that cone is of codimension
$L\ni p$
. The singular set of that cone is of codimension
![]() $\geqslant 6$
(Proposition 4.2), and so for a general line
$\geqslant 6$
(Proposition 4.2), and so for a general line
![]() $L\ni p$
,
$L\ni p$
,
so that
![]() $L\cap \mathop {\mathrm {Sing}}E_X=\emptyset $
, and the same is true for every hyperplane section of the cone
$L\cap \mathop {\mathrm {Sing}}E_X=\emptyset $
, and the same is true for every hyperplane section of the cone
![]() $E_X\cap T_pE_X$
, containing the point p, since its singular set is of codimension
$E_X\cap T_pE_X$
, containing the point p, since its singular set is of codimension
![]() $\geqslant 4$
(Remark 1.4).
$\geqslant 4$
(Remark 1.4).
Let
![]() ${\cal L}(p)$
be the union of all lines
${\cal L}(p)$
be the union of all lines
![]() $L\subset E_X,L\ni p$
, such that
$L\subset E_X,L\ni p$
, such that
Obviously,
![]() ${\cal L}(p)$
is the section of the cone
${\cal L}(p)$
is the section of the cone
![]() $E_X\cap T_pE_X$
by some hyperplane, containing the point p (this hyperplane corresponds to the hyperplane
$E_X\cap T_pE_X$
by some hyperplane, containing the point p (this hyperplane corresponds to the hyperplane
![]() $\Theta _E(p$
)). As we have shown above,
$\Theta _E(p$
)). As we have shown above,
![]() ${\cal L}(p)$
is an irreducible closed subset of codimension
${\cal L}(p)$
is an irreducible closed subset of codimension
![]() $k+1$
in
$k+1$
in
![]() $E_X$
, and
$E_X$
, and
Set
 $$ \begin{align*}\Lambda=\overline{\mathop{\bigcup}\limits_{p\in U_B}{\cal L}(p)} \end{align*} $$
$$ \begin{align*}\Lambda=\overline{\mathop{\bigcup}\limits_{p\in U_B}{\cal L}(p)} \end{align*} $$
(the overline means the closure). By what was said above, the inequality
holds.
Theorem 5.2. The subset
![]() $\Lambda \subset E_X$
is a hyperplane section of the variety
$\Lambda \subset E_X$
is a hyperplane section of the variety
![]() $E_X\subset {\mathbb E}_X$
.
$E_X\subset {\mathbb E}_X$
.
We will prove Theorem 5.2 in two steps: first, we will show that
![]() $\Lambda $
is a prime divisor on
$\Lambda $
is a prime divisor on
![]() $E_X$
and then that this divisor is a hyperplane section. By construction, the set
$E_X$
and then that this divisor is a hyperplane section. By construction, the set
![]() $\Lambda $
is irreducible.
$\Lambda $
is irreducible.
5.3 The set
 $\Lambda $
is a divisor
$\Lambda $
is a divisor
By our assumption about the rank of the point
![]() $o\in X$
for
$o\in X$
for
![]() $b=k+1$
, the inequality
$b=k+1$
, the inequality
holds. By Corollary 4.3, for a general subspace
![]() $\Pi \subset E_X$
of dimension b, the restriction onto B of the projection
$\Pi \subset E_X$
of dimension b, the restriction onto B of the projection
from the subspace
![]() $\Pi $
is dominant. Let
$\Pi $
is dominant. Let
![]() $s\in {\mathbb P}^{N(X)-b-2}$
be a point of general position. By the symbol
$s\in {\mathbb P}^{N(X)-b-2}$
be a point of general position. By the symbol
![]() $\langle \Pi ,s\rangle $
denote the closure
$\langle \Pi ,s\rangle $
denote the closure
(this is a
![]() $(\mathop {\mathrm {dim}}\Pi +1)$
-dimensional subspace) and set
$(\mathop {\mathrm {dim}}\Pi +1)$
-dimensional subspace) and set
For the blow-ups
![]() $\sigma \colon \widetilde {E}_X\to E_X$
and
$\sigma \colon \widetilde {E}_X\to E_X$
and
![]() $\sigma _{\mathbb P}\colon \widetilde {{\mathbb P}^{N(X)-1}}\to {\mathbb P}^{N(X)-1}$
of the subspace
$\sigma _{\mathbb P}\colon \widetilde {{\mathbb P}^{N(X)-1}}\to {\mathbb P}^{N(X)-1}$
of the subspace
![]() $\Pi $
on
$\Pi $
on
![]() $E_X$
and
$E_X$
and
![]() ${\mathbb P}^{N(X)-1}$
, respectively, let
${\mathbb P}^{N(X)-1}$
, respectively, let
![]() $\varphi \colon \widetilde {E}_X\to {\mathbb P}^{N(X)-b-2}$
and
$\varphi \colon \widetilde {E}_X\to {\mathbb P}^{N(X)-b-2}$
and
![]() $\varphi _{\mathbb P}\colon \widetilde {{\mathbb P}^{N(X)-1}}\to {\mathbb P}^{N(X)-b-2}$
be the regularizations of the projections
$\varphi _{\mathbb P}\colon \widetilde {{\mathbb P}^{N(X)-1}}\to {\mathbb P}^{N(X)-b-2}$
be the regularizations of the projections
![]() $\mathop {\mathrm {pr}}_{\Pi }|_{E_X}$
and
$\mathop {\mathrm {pr}}_{\Pi }|_{E_X}$
and
![]() $\mathop {\mathrm {pr}}_{\Pi }$
, respectively. Obviously, the fibre
$\mathop {\mathrm {pr}}_{\Pi }$
, respectively. Obviously, the fibre
![]() $\varphi ^{-1}_{\mathbb P}(s)$
identifies naturally with
$\varphi ^{-1}_{\mathbb P}(s)$
identifies naturally with
![]() $\langle \Pi ,s\rangle $
, and the fibre
$\langle \Pi ,s\rangle $
, and the fibre
![]() $\varphi ^{-1}(s)$
with
$\varphi ^{-1}(s)$
with
![]() $E_X(\Pi ,s)$
. The fibre of the surjective morphism
$E_X(\Pi ,s)$
. The fibre of the surjective morphism
![]() $\varphi |_{\sigma ^{-1}(B)}$
over the point s we denote by the symbol
$\varphi |_{\sigma ^{-1}(B)}$
over the point s we denote by the symbol
![]() $B(s)$
; this is a possibly reducible closed subset in
$B(s)$
; this is a possibly reducible closed subset in
![]() $\varphi ^{-1}_{\mathbb P}(s)$
, each irreducible component of which is of codimension
$\varphi ^{-1}_{\mathbb P}(s)$
, each irreducible component of which is of codimension
![]() $c_B=\mathop {\mathrm {codim}} (B\subset E_X)$
and is not contained entirely in the hyperplane
$c_B=\mathop {\mathrm {codim}} (B\subset E_X)$
and is not contained entirely in the hyperplane
![]() $\Pi $
(with respect to the identification
$\Pi $
(with respect to the identification
![]() $\varphi ^{-1}_{\mathbb P}(s)=\langle \Pi ,s\rangle $
). Write down
$\varphi ^{-1}_{\mathbb P}(s)=\langle \Pi ,s\rangle $
). Write down
![]() $B(s)$
as a union of irreducible components:
$B(s)$
as a union of irreducible components:
and let
![]() $p\in B_i(s)$
be a point of general position on one of them; in particular,
$p\in B_i(s)$
be a point of general position on one of them; in particular,
![]() $p\not \in \Pi $
, so that the projection
$p\not \in \Pi $
, so that the projection
![]() $\mathop {\mathrm {pr}}\nolimits _{\Pi }$
is regular at that point and
$\mathop {\mathrm {pr}}\nolimits _{\Pi }$
is regular at that point and
![]() $p\not \in B_j(s)$
for
$p\not \in B_j(s)$
for
![]() $j\neq i$
. We will consider the point p as a point of general position on B, which was introduced in Subsection 5.1, and use the notations for the blow-up
$j\neq i$
. We will consider the point p as a point of general position on B, which was introduced in Subsection 5.1, and use the notations for the blow-up
![]() $\varphi _p$
of this point and for objects linked to this blow-up. Note that for
$\varphi _p$
of this point and for objects linked to this blow-up. Note that for
![]() $b=k+1$
, we have the inequality
$b=k+1$
, we have the inequality
The set of lines
![]() $L\subset E_X(\Pi ,s)$
,
$L\subset E_X(\Pi ,s)$
,
![]() $L\ni p$
, such that
$L\ni p$
, such that
![]() $L^{(p)}\cap E(p)\in \Theta (p)$
, forms a hyperplane in
$L^{(p)}\cap E(p)\in \Theta (p)$
, forms a hyperplane in
![]() $E_X(\Pi ,s)$
, which we denote by the symbol
$E_X(\Pi ,s)$
, which we denote by the symbol
![]() $\Lambda (\Pi ,s,p)$
. By construction,
$\Lambda (\Pi ,s,p)$
. By construction,
![]() $\Lambda (\Pi ,s,p)\subset \Lambda $
.
$\Lambda (\Pi ,s,p)\subset \Lambda $
.
Since any nontrivial algebraic family of hyperplanes in a projective space sweeps out that space and for a general point s we have
![]() $E_X(\Pi ,s)\not \subset \Lambda $
(otherwise,
$E_X(\Pi ,s)\not \subset \Lambda $
(otherwise,
![]() $\Lambda =E_X$
, which is impossible), we conclude that the hyperplane
$\Lambda =E_X$
, which is impossible), we conclude that the hyperplane
![]() $\Lambda (\Pi ,s,p)$
does not depend on the choice of a point of general position
$\Lambda (\Pi ,s,p)$
does not depend on the choice of a point of general position
![]() $p\in B_i(s)$
, so that
$p\in B_i(s)$
, so that
is a hyperplane in
![]() $\varphi ^{-1}(s)=E_X(\Pi ,s)$
, containing the component
$\varphi ^{-1}(s)=E_X(\Pi ,s)$
, containing the component
![]() $B_i(s)$
. Therefore, for a general point s, the intersection
$B_i(s)$
. Therefore, for a general point s, the intersection
![]() $\Lambda \cap E_X(\Pi ,s)$
contains a divisor in
$\Lambda \cap E_X(\Pi ,s)$
contains a divisor in
![]() $E_X(\Pi ,s)$
, whence we get that
$E_X(\Pi ,s)$
, whence we get that
![]() $\Lambda \subset E_X$
is a (prime) divisor on
$\Lambda \subset E_X$
is a (prime) divisor on
![]() $E_X$
, as we claimed. This divisor is cut out on
$E_X$
, as we claimed. This divisor is cut out on
![]() $E_X$
by a hypersurface of degree
$E_X$
by a hypersurface of degree
![]() $d_{\Lambda }$
in
$d_{\Lambda }$
in
![]() ${\mathbb E}_X$
. It remains to show that
${\mathbb E}_X$
. It remains to show that
![]() $d_{\Lambda }=1$
.
$d_{\Lambda }=1$
.
Remark 5.2. We promised above that the option
![]() $(2)_{\Theta }$
does not take place. Indeed, if it does, then every line
$(2)_{\Theta }$
does not take place. Indeed, if it does, then every line
![]() $L\ni p$
in
$L\ni p$
in
![]() $E_X(\Pi ,s)$
is contained in
$E_X(\Pi ,s)$
is contained in
![]() $\Lambda $
, so that
$\Lambda $
, so that
![]() $E_X(\Pi ,s)\subset \Lambda $
, and for that reason,
$E_X(\Pi ,s)\subset \Lambda $
, and for that reason,
![]() $E_X\subset \Lambda $
, which is absurd. In a similar way, if
$E_X\subset \Lambda $
, which is absurd. In a similar way, if
![]() $\mathop {\mathrm {mult}}_BD^+>\nu (D)$
, then every line in
$\mathop {\mathrm {mult}}_BD^+>\nu (D)$
, then every line in
![]() $E_X(\Pi ,s)$
, meeting B, is contained in
$E_X(\Pi ,s)$
, meeting B, is contained in
![]() $\Lambda $
, so that
$\Lambda $
, so that
![]() $E_X\subset \Lambda $
, which is impossible. Therefore, the inequality
$E_X\subset \Lambda $
, which is impossible. Therefore, the inequality
holds.
5.4 The divisor
 $\Lambda $
is a hyperplane section
$\Lambda $
is a hyperplane section
Let us consider the intersection
![]() $\Lambda \cap E_X(\Pi ,s)$
for a general point s in more details. This is a possibly reducible divisor, each component of which has multiplicity 1, containing at least one hyperplane. If in this divisor there are components of degree
$\Lambda \cap E_X(\Pi ,s)$
for a general point s in more details. This is a possibly reducible divisor, each component of which has multiplicity 1, containing at least one hyperplane. If in this divisor there are components of degree
![]() $\geqslant 2$
, then the union of hyperplanes in
$\geqslant 2$
, then the union of hyperplanes in
![]() $\Lambda (\Pi ,s)$
gives a proper closed subset of
$\Lambda (\Pi ,s)$
gives a proper closed subset of
![]() $\Lambda _1(\Pi ,s)$
, which is also a divisor. Then
$\Lambda _1(\Pi ,s)$
, which is also a divisor. Then
 $$ \begin{align*}\overline{\bigcup_s\Lambda_1(\Pi,s)} \end{align*} $$
$$ \begin{align*}\overline{\bigcup_s\Lambda_1(\Pi,s)} \end{align*} $$
(the union is taken over a nonempty open subset in
![]() ${\mathbb P}^{N(X)-b-2}$
) is a proper closed subset in
${\mathbb P}^{N(X)-b-2}$
) is a proper closed subset in
![]() $\Lambda $
, which is of codimension 1 in
$\Lambda $
, which is of codimension 1 in
![]() $E_X$
, which is impossible as
$E_X$
, which is impossible as
![]() $\Lambda $
is a prime divisor. We conclude that
$\Lambda $
is a prime divisor. We conclude that
![]() $\Lambda (\Pi ,s)$
is a union of precisely
$\Lambda (\Pi ,s)$
is a union of precisely
![]() $d_{\Lambda }$
distinct hyperplanes in
$d_{\Lambda }$
distinct hyperplanes in
![]() $E_X(\Pi ,s)$
.
$E_X(\Pi ,s)$
.
Assume that
![]() $d_{\Lambda }\geqslant 2$
. By our assumptions about the rank
$d_{\Lambda }\geqslant 2$
. By our assumptions about the rank
![]() $\mathop {\mathrm {rk}}(o\in X)$
, the inequality (19) holds for
$\mathop {\mathrm {rk}}(o\in X)$
, the inequality (19) holds for
![]() $b=3k$
:
$b=3k$
:
Again, we apply Corollary 4.3, now to a general subspace
![]() $\Pi ^*=E_X(\Pi ,s)$
of dimension
$\Pi ^*=E_X(\Pi ,s)$
of dimension
![]() $b^*=b+1-k\geqslant 2k+1$
. The subspace
$b^*=b+1-k\geqslant 2k+1$
. The subspace
![]() $\Pi ^*$
does not meet the set
$\Pi ^*$
does not meet the set
![]() $\mathop {\mathrm {Sing}} E_X$
, and the restriction of the projection from
$\mathop {\mathrm {Sing}} E_X$
, and the restriction of the projection from
![]() $\Pi ^*$
$\Pi ^*$
onto B is dominant. Let
![]() $s^*\in {\mathbb P}^{N(X)-b^*-2}$
be a point of general position. We use the notations introduced above and write
$s^*\in {\mathbb P}^{N(X)-b^*-2}$
be a point of general position. We use the notations introduced above and write
![]() $E_X(\Pi ^*,s^*)$
. For the blow-ups of the subspace
$E_X(\Pi ^*,s^*)$
. For the blow-ups of the subspace
![]() $\Pi ^*$
, we use the symbols
$\Pi ^*$
, we use the symbols
![]() $\sigma _{\Pi ^*}$
and
$\sigma _{\Pi ^*}$
and
![]() $\sigma _{{\mathbb P},\Pi ^*}$
, respectively, and for the regularized projections, the symbols
$\sigma _{{\mathbb P},\Pi ^*}$
, respectively, and for the regularized projections, the symbols
![]() $\varphi _{\Pi ^*}$
and
$\varphi _{\Pi ^*}$
and
![]() $\varphi _{{\mathbb P},\Pi ^*}$
. The symbol
$\varphi _{{\mathbb P},\Pi ^*}$
. The symbol
![]() $\langle \Pi ^*,s^*\rangle $
has the same meaning as above. Set
$\langle \Pi ^*,s^*\rangle $
has the same meaning as above. Set
to be the exceptional divisors of the blow-up of
![]() $\Pi ^*$
on
$\Pi ^*$
on
![]() $E_X$
and
$E_X$
and
![]() ${\mathbb P}^{N(X)-1}$
. By the arguments immediately before the statement of Proposition 4.5, the map
${\mathbb P}^{N(X)-1}$
. By the arguments immediately before the statement of Proposition 4.5, the map
![]() $\varphi _{\Pi ^*}|_{E^*}$
is surjective, and by Proposition 4.5 (which applies since
$\varphi _{\Pi ^*}|_{E^*}$
is surjective, and by Proposition 4.5 (which applies since
![]() $b^*\geqslant k+1$
), the intersection
$b^*\geqslant k+1$
), the intersection
is nonempty, and each of its irreducible components is of codimension 1 in the projective space
![]() $\varphi _{\Pi ^*}^{-1}(s^*)\cap E^*_{\mathbb P}$
.
$\varphi _{\Pi ^*}^{-1}(s^*)\cap E^*_{\mathbb P}$
.
By what was shown above,
![]() $\Lambda \cap {\Pi ^*}$
is a union of
$\Lambda \cap {\Pi ^*}$
is a union of
![]() $d_{\Lambda }$
distinct hyperplanes
$d_{\Lambda }$
distinct hyperplanes
![]() $\Lambda ^*_i$
,
$\Lambda ^*_i$
,
![]() $i\in I$
. In a similar way,
$i\in I$
. In a similar way,
is the union of
![]() $d_{\Lambda }$
distinct hyperplanes in
$d_{\Lambda }$
distinct hyperplanes in
![]() $\varphi ^{-1}_{\Pi ^*}(s^*)$
, none of which coincides with the hyperplane
$\varphi ^{-1}_{\Pi ^*}(s^*)$
, none of which coincides with the hyperplane
![]() $\varphi ^{-1}_{\Pi ^*}(s^*)\cap E_{\mathbb P}^*$
. Note that the strict transform of the divisor
$\varphi ^{-1}_{\Pi ^*}(s^*)\cap E_{\mathbb P}^*$
. Note that the strict transform of the divisor
![]() $\Lambda $
with respect to the blow-up
$\Lambda $
with respect to the blow-up
![]() $\sigma _{\Pi ^*}$
is just its full inverse image
$\sigma _{\Pi ^*}$
is just its full inverse image
![]() $\sigma ^{-1}_{\Pi ^*}(\Lambda )$
, since
$\sigma ^{-1}_{\Pi ^*}(\Lambda )$
, since
![]() $\Lambda \not \subset \Pi ^*$
. Furthermore,
$\Lambda \not \subset \Pi ^*$
. Furthermore,
and every intersection
![]() $\varphi ^{-1}_{\Pi ^*}(s^*)\cap \sigma ^{-1}_{\Pi ^*}(\Lambda ^*_i)$
is a hyperplane in
$\varphi ^{-1}_{\Pi ^*}(s^*)\cap \sigma ^{-1}_{\Pi ^*}(\Lambda ^*_i)$
is a hyperplane in
![]() $\varphi ^{-1}_{\Pi ^*}(s^*)\cap E^*_{\mathbb P}$
. It follows that each irreducible component of set
$\varphi ^{-1}_{\Pi ^*}(s^*)\cap E^*_{\mathbb P}$
. It follows that each irreducible component of set
![]() $\Lambda \cap E_X(\Pi ^*,s^*)$
intersects the hyperplane
$\Lambda \cap E_X(\Pi ^*,s^*)$
intersects the hyperplane
![]() $\varphi ^{-1}_{\Pi ^*}(s^*)\cap E^*_{\mathbb P}$
by one of the hyperplanes
$\varphi ^{-1}_{\Pi ^*}(s^*)\cap E^*_{\mathbb P}$
by one of the hyperplanes
![]() $\sigma ^{-1}_{\Pi ^*}(\Lambda ^*_i)\cap \varphi ^{-1}_{\Pi ^*}(s^*)$
,
$\sigma ^{-1}_{\Pi ^*}(\Lambda ^*_i)\cap \varphi ^{-1}_{\Pi ^*}(s^*)$
,
![]() $i\in I$
. Thus, one can write down
$i\in I$
. Thus, one can write down
where
![]() $\Lambda _i(\Pi ^*,s^*)$
is a hyperplane in
$\Lambda _i(\Pi ^*,s^*)$
is a hyperplane in
![]() $E_X(\Pi ^*,s^*)$
, satisfying the equality
$E_X(\Pi ^*,s^*)$
, satisfying the equality
In other words, the choice of a component of the intersection
![]() $\Lambda \cap \Pi ^*$
determines uniquely the component of the intersection of
$\Lambda \cap \Pi ^*$
determines uniquely the component of the intersection of
![]() $\Lambda $
with
$\Lambda $
with
![]() $\langle \Pi ^*,s^*\rangle =\varphi ^{-1}_{\Pi ^*}(s^*)=E_X(\Pi ^*,s^*)$
for a general point
$\langle \Pi ^*,s^*\rangle =\varphi ^{-1}_{\Pi ^*}(s^*)=E_X(\Pi ^*,s^*)$
for a general point
![]() $s^*$
. Now set
$s^*$
. Now set
 $$ \begin{align*}\Lambda_i=\sigma_{\Pi^*}\left(\overline{\mathop{\bigcup}\limits_{s^*} (\Pi^*,s^*)}\right), \end{align*} $$
$$ \begin{align*}\Lambda_i=\sigma_{\Pi^*}\left(\overline{\mathop{\bigcup}\limits_{s^*} (\Pi^*,s^*)}\right), \end{align*} $$
where the union is taken over a nonempty Zariski open subset of the projective space
![]() ${\mathbb P}^{N(X)-b^*-2}$
. This is a prime divisor on
${\mathbb P}^{N(X)-b^*-2}$
. This is a prime divisor on
![]() $E_X$
, and moreover,
$E_X$
, and moreover,
![]() $\Lambda _i\subset \Lambda $
, and for that reason,
$\Lambda _i\subset \Lambda $
, and for that reason,
![]() $\Lambda _i=\Lambda $
, whence we conclude that all hyperplanes
$\Lambda _i=\Lambda $
, whence we conclude that all hyperplanes
![]() $\Lambda _i(\Pi ^*,s^*)$
are the same, which is a contradiction with the assumption that
$\Lambda _i(\Pi ^*,s^*)$
are the same, which is a contradiction with the assumption that
![]() $d_{\Lambda }\geqslant 2$
.
$d_{\Lambda }\geqslant 2$
.
Thus,
![]() $d_{\Lambda }=1$
and
$d_{\Lambda }=1$
and
![]() $\Lambda $
is a hyperplane section of
$\Lambda $
is a hyperplane section of
![]() $E_X\subset {\mathbb E}_X$
. Q.E.D. for Theorem 5.2, and therefore for Theorem 5.1.
$E_X\subset {\mathbb E}_X$
. Q.E.D. for Theorem 5.2, and therefore for Theorem 5.1.
5.5 The construction of a new working triple
Now we can complete the proof Theorem 3.3 and construct the new working triple
![]() $(R,D_R,o)$
. Let
$(R,D_R,o)$
. Let
![]() $R\ni o$
the section of X by the hyperplane
$R\ni o$
the section of X by the hyperplane
![]() ${\mathbb P}(R)=\langle R\rangle $
, such that
${\mathbb P}(R)=\langle R\rangle $
, such that
(in other words, the hyperplane
![]() ${\mathbb P}(R)^+ \cap {\mathbb E}_X$
cuts out
${\mathbb P}(R)^+ \cap {\mathbb E}_X$
cuts out
![]() $\Lambda $
on
$\Lambda $
on
![]() $E_X$
). Since R is not a component of the effective divisor
$E_X$
). Since R is not a component of the effective divisor
![]() $D_X$
, the scheme-theoretic intersection
$D_X$
, the scheme-theoretic intersection
![]() $(R\circ D_X)$
is well defined, and we treat this intersection as an effective divisor on R. Set
$(R\circ D_X)$
is well defined, and we treat this intersection as an effective divisor on R. Set
![]() $D_R=(R\circ D_X)$
in that sense.
$D_R=(R\circ D_X)$
in that sense.
On
![]() $R^+\subset X^+$
with the exceptional divisor
$R^+\subset X^+$
with the exceptional divisor
we have the equivalence
where
![]() $H_R$
is the class of a hyperplane section of R and
$H_R$
is the class of a hyperplane section of R and
Again,
![]() $[R,o]$
is a marked complete intersection, of level
$[R,o]$
is a marked complete intersection, of level
![]() $(k,c_R)$
, where
$(k,c_R)$
, where
![]() $c_R=c_X-2$
,
$c_R=c_X-2$
,
![]() $(R,D_R,o)$
is a working triple, and the inequality
$(R,D_R,o)$
is a working triple, and the inequality
 $$ \begin{align*}2n(D_R)-\nu(D_R)<\left(1-\frac{1}{k+1}\right)(2n(D_X)-\nu(D_X)) \end{align*} $$
$$ \begin{align*}2n(D_R)-\nu(D_R)<\left(1-\frac{1}{k+1}\right)(2n(D_X)-\nu(D_X)) \end{align*} $$
holds (since
![]() $n(D_R)=n(D_X)$
).
$n(D_R)=n(D_X)$
).
The procedure of constructing the special hyperplane section is complete. Q.E.D. for Theorem 3.3.
6 Multiplicity of a line
In this section, we prove Proposition 5.3.
6.1 Blowing up a point and a curve
Since we completed our study of working triples, the symbol X is now free and will mean an arbitrary non-singular quasi-projective variety of dimension
![]() $\geqslant 3$
. Let
$\geqslant 3$
. Let
![]() $C\subset X$
be a non-singular projective curve,
$C\subset X$
be a non-singular projective curve,
![]() $p\in C$
a point. Furthermore, let
$p\in C$
a point. Furthermore, let
be the blow-up of the curve C with the exceptional divisor
![]() $E_C$
and
$E_C$
and
![]() $\sigma ^{-1}_C(p)\cong {\mathbb P}^{\dim X-2}$
the fibre over the point p. Let
$\sigma ^{-1}_C(p)\cong {\mathbb P}^{\dim X-2}$
the fibre over the point p. Let
be the blow-up of that fibre with the exceptional divisor E and
![]() $E_C^{(p)}$
the strict transform of
$E_C^{(p)}$
the strict transform of
![]() $E_C$
on that blow-up.
$E_C$
on that blow-up.
However, consider the blow-up
of the point p with the exceptional divisor
![]() $E_p$
and denote by the symbol
$E_p$
and denote by the symbol
![]() $C(p)$
the strict transform of the curve C on
$C(p)$
the strict transform of the curve C on
![]() $X(p)$
. Finally, let
$X(p)$
. Finally, let
be the blow-up of the curve
![]() $C(p)$
,
$C(p)$
,
![]() $E_{C(p)}$
the exceptional divisor of that blow-up and
$E_{C(p)}$
the exceptional divisor of that blow-up and
![]() $E^C_p$
the strict transform of
$E^C_p$
the strict transform of
![]() $E_p$
.
$E_p$
.
Proposition 6.1. The identity map
![]() $\mathop {\mathrm {id}}_X$
extends to an isomorphism
$\mathop {\mathrm {id}}_X$
extends to an isomorphism
identifying the subvarieties E and
![]() $E^C_p$
and the subvarieties
$E^C_p$
and the subvarieties
![]() $E^p_C$
and
$E^p_C$
and
![]() $E_{C(p)}$
.
$E_{C(p)}$
.
Proof. This is a well-known fact, which can be checked by elementary computations in local parameters. Q.E.D. for the proposition.
Taking into account the identifications above, we will use the notations
![]() $E^C_p$
and
$E^C_p$
and
![]() $E_{C(p)}$
, and forget about E and
$E_{C(p)}$
, and forget about E and
![]() $E^p_C$
. The variety
$E^p_C$
. The variety
![]() $X(C,\sigma ^{-1}_C(p))$
will be denoted by the symbol
$X(C,\sigma ^{-1}_C(p))$
will be denoted by the symbol
![]() $\widetilde {X}$
. Let D be an effective divisor on X. The symbols
$\widetilde {X}$
. Let D be an effective divisor on X. The symbols
![]() $D^C$
and
$D^C$
and
![]() $D^p$
stand for its strict transforms on
$D^p$
stand for its strict transforms on
![]() $X(C)$
and
$X(C)$
and
![]() $X(p)$
, respectively, and the symbol
$X(p)$
, respectively, and the symbol
![]() $\widetilde {D}$
for its strict transform on
$\widetilde {D}$
for its strict transform on
![]() $\widetilde {X}$
. Set
$\widetilde {X}$
. Set
where, of course,
![]() $\mu _p\geqslant \mu $
.
$\mu _p\geqslant \mu $
.
Lemma 6.1. The following equality holds:
Proof. (This is a well-known fact, and we give a proof for the convenience of the reader, and also because a similar argument is used below.) We have the sequence of obvious equalities:
so that
Considering the second sequence of blow-ups, we get
and, respectively,
Comparing the two presentations of the same effective divisor, we get the claim of the lemma.
6.2 Blowing up two points and a curve
In the notations of the previous subsection, let us consider the point
Set
![]() $\mu _q=\mathop {\mathrm {mult}}_qD^p$
. Obviously,
$\mu _q=\mathop {\mathrm {mult}}_qD^p$
. Obviously,
Let
be the blow-up of the point q with the exceptional divisor
![]() $E_q$
and
$E_q$
and
![]() $C(p,q)$
the strict transform of the curve
$C(p,q)$
the strict transform of the curve
![]() $C(p)$
. Finally, let
$C(p)$
. Finally, let
be the blow-up of the curve
![]() $C(p,q)$
with the exceptional divisor
$C(p,q)$
with the exceptional divisor
![]() $E_{C(p,q)}$
and
$E_{C(p,q)}$
and
![]() $E^{\sharp }_q$
the strict transform of
$E^{\sharp }_q$
the strict transform of
![]() $E_q$
. Note that the curve
$E_q$
. Note that the curve
![]() $C(p)$
intersects
$C(p)$
intersects
![]() $E_p$
transversally, and therefore,
$E_p$
transversally, and therefore,
![]() $C(p,q)$
does not meet the strict transform
$C(p,q)$
does not meet the strict transform
![]() $E^q_p$
of the divisor
$E^q_p$
of the divisor
![]() $E_p\subset X(p)$
on
$E_p\subset X(p)$
on
![]() $X(p,q)$
.
$X(p,q)$
.
Proposition 6.2. The restriction of the divisor
![]() $D^C$
onto the exceptional divisor
$D^C$
onto the exceptional divisor
![]() $E_C$
contains the fibre
$E_C$
contains the fibre
![]() $\sigma ^{-1}_C(p)$
with multiplicity at least
$\sigma ^{-1}_C(p)$
with multiplicity at least
![]() $\mu _p+\mu _q-2\mu $
.
$\mu _p+\mu _q-2\mu $
.
Proof. Obviously, on
![]() $X^{\sharp }$
we have the equality
$X^{\sharp }$
we have the equality
where
![]() $D^{\sharp }$
is the strict transform of D on
$D^{\sharp }$
is the strict transform of D on
![]() $X^{\sharp }$
. However, using the constructions of Subsection 6.1, we see that
$X^{\sharp }$
. However, using the constructions of Subsection 6.1, we see that
![]() $X^{\sharp }$
can be obtained as the blow-up of the curve
$X^{\sharp }$
can be obtained as the blow-up of the curve
![]() $C(p)$
on
$C(p)$
on
![]() $X(p)$
with the subsequent blowing up of the fibre of the exceptional divisor
$X(p)$
with the subsequent blowing up of the fibre of the exceptional divisor
![]() $E_{C(p)}$
over the point q or, applying the construction of Subsection 6.1 twice, as the blow-up of the curve C on X with the subsequent blowing up of the fibre
$E_{C(p)}$
over the point q or, applying the construction of Subsection 6.1 twice, as the blow-up of the curve C on X with the subsequent blowing up of the fibre
![]() $\sigma ^{-1}_C(p)$
and then the blowing up of the subvariety
$\sigma ^{-1}_C(p)$
and then the blowing up of the subvariety
In the last presentation, the three prime exceptional divisors are
We denote the blow-up
![]() $X^{\sharp }\to \widetilde {X}$
of the subvariety
$X^{\sharp }\to \widetilde {X}$
of the subvariety
![]() $E^C_p\cap E^p_C$
, mentioned above, by the symbol
$E^C_p\cap E^p_C$
, mentioned above, by the symbol
![]() $\sigma _{\sharp }$
. Thus, we obtain the following commutative diagram of birational morphisms:
$\sigma _{\sharp }$
. Thus, we obtain the following commutative diagram of birational morphisms:
 $$ \begin{align*}\begin{array}{ccccc} X(C) & \stackrel{\sigma}{\leftarrow} & \widetilde{X} & \stackrel{\sigma_{\sharp}}{\leftarrow} & X^{\sharp}\\ \downarrow & & \downarrow & & \downarrow\\ X &\stackrel{\varphi_p}{\leftarrow} & X(p) &\stackrel{\varphi_q}{\leftarrow} & X(p,q),\\ \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccccc} X(C) & \stackrel{\sigma}{\leftarrow} & \widetilde{X} & \stackrel{\sigma_{\sharp}}{\leftarrow} & X^{\sharp}\\ \downarrow & & \downarrow & & \downarrow\\ X &\stackrel{\varphi_p}{\leftarrow} & X(p) &\stackrel{\varphi_q}{\leftarrow} & X(p,q),\\ \end{array} \end{align*} $$
where the vertical arrows (from the left to the right) are
![]() $\sigma _C$
,
$\sigma _C$
,
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi _{\sharp }$
, respectively. We have the equality
$\varphi _{\sharp }$
, respectively. We have the equality
This pullback can be written down as
since
![]() $E_{C(p,q)}=E^{\sharp }_C$
and
$E_{C(p,q)}=E^{\sharp }_C$
and
![]() $E^{\sharp }_q$
is the exceptional divisor of the blow-up
$E^{\sharp }_q$
is the exceptional divisor of the blow-up
![]() $\sigma _{\sharp }$
. However,
$\sigma _{\sharp }$
. However,
![]() $D^C=\sigma ^{*}_C D-\mu E_C$
and, besides,
$D^C=\sigma ^{*}_C D-\mu E_C$
and, besides,
so that the exceptional divisor
![]() $E^{\sharp }_q$
comes into the pullback of the divisor
$E^{\sharp }_q$
comes into the pullback of the divisor
![]() $D^C$
on
$D^C$
on
![]() $X^{\sharp }$
with multiplicity
$X^{\sharp }$
with multiplicity
![]() $(\mu _p+\mu _q-2\mu )$
. However, the blow-ups
$(\mu _p+\mu _q-2\mu )$
. However, the blow-ups
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma _{\sharp }$
do not change the divisor
$\sigma _{\sharp }$
do not change the divisor
![]() $E_C$
, as they blow-up subvarieties of codimension 1 on the variety:
$E_C$
, as they blow-up subvarieties of codimension 1 on the variety:
is an isomorphism. Since the restriction
![]() $D^{\sharp }$
onto
$D^{\sharp }$
onto
![]() $E^{\sharp }_C$
is an effective divisor, it follows from here that the restriction of the divisor
$E^{\sharp }_C$
is an effective divisor, it follows from here that the restriction of the divisor
![]() $D^C$
onto
$D^C$
onto
![]() $E_C$
contains the fibre
$E_C$
contains the fibre
![]() $\sigma ^{-1}(p)$
(which is precisely the restriction of
$\sigma ^{-1}(p)$
(which is precisely the restriction of
![]() $E^{\sharp }_q$
onto
$E^{\sharp }_q$
onto
![]() $E^{\sharp }_C$
in terms of the isomorphism between
$E^{\sharp }_C$
in terms of the isomorphism between
![]() $E^{\sharp }_C$
and
$E^{\sharp }_C$
and
![]() $E_C$
, discussed above) with multiplicity
$E_C$
, discussed above) with multiplicity
![]() $\geqslant \mu _p+\mu _q-2\mu $
. Proof of Proposition 6.2 is complete.
$\geqslant \mu _p+\mu _q-2\mu $
. Proof of Proposition 6.2 is complete.
6.3 The multiplicity of an infinitely near line
Let us come back to the proof of Proposition 5.3. We will obtain its claim from a more general fact. Let
![]() $o\in {\cal X}$
be a germ of a multi-quadratic singularity of type
$o\in {\cal X}$
be a germ of a multi-quadratic singularity of type
![]() $2^k$
, where
$2^k$
, where
![]() ${\cal X}\subset {\cal Y}$
,
${\cal X}\subset {\cal Y}$
,
![]() ${\cal Y}$
is non-singular,
${\cal Y}$
is non-singular,
![]() $\mathop {\mathrm {codim}}({\cal X}\subset {\cal Y})=k$
and the inequality
$\mathop {\mathrm {codim}}({\cal X}\subset {\cal Y})=k$
and the inequality
holds, so that
![]() $\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}{\cal X}\subset {\cal X})\geqslant 4$
and
$\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}{\cal X}\subset {\cal X})\geqslant 4$
and
![]() ${\cal X}$
is factorial. Let
${\cal X}$
is factorial. Let
![]() $\sigma _{\cal Y}\colon {\cal Y}^+\to {\cal Y}$
be the blow-up of the point o with the exceptional divisor
$\sigma _{\cal Y}\colon {\cal Y}^+\to {\cal Y}$
be the blow-up of the point o with the exceptional divisor
![]() $E_{\cal Y}$
,
$E_{\cal Y}$
,
![]() ${\cal X}^+\subset {\cal Y}^+$
the strict transform, so that
${\cal X}^+\subset {\cal Y}^+$
the strict transform, so that
is the blow-up of the point o on
![]() ${\cal X}$
with the exceptional divisor
${\cal X}$
with the exceptional divisor
![]() $E_{\cal X}$
, which is a complete intersection of k quadrics in
$E_{\cal X}$
, which is a complete intersection of k quadrics in
![]() $E_{\cal Y}\cong {\mathbb P}^{\mathrm {dim{\cal Y}-1}}$
. By Proposition 4.2,
$E_{\cal Y}\cong {\mathbb P}^{\mathrm {dim{\cal Y}-1}}$
. By Proposition 4.2,
Let
![]() $L\subset E_{\cal X}$
be a line, where
$L\subset E_{\cal X}$
be a line, where
![]() $L\cap \mathop {\mathrm {Sing}} E_{\cal X}=\emptyset $
and
$L\cap \mathop {\mathrm {Sing}} E_{\cal X}=\emptyset $
and
![]() $p\in L$
a point. Let us blow-up this point on
$p\in L$
a point. Let us blow-up this point on
![]() ${\cal Y}^+$
and
${\cal Y}^+$
and
![]() ${\cal X}^+$
, respectively:
${\cal X}^+$
, respectively:
are these blow-ups with the exceptional divisors
![]() $E_{p,{\cal Y}}$
and
$E_{p,{\cal Y}}$
and
![]() $E_p$
. Set
$E_p$
. Set
where
![]() $L^{(p)}\subset {\cal X}_p$
is the strict transform.
$L^{(p)}\subset {\cal X}_p$
is the strict transform.
Let
![]() $D_{\cal X}$
be an effective divisor on
$D_{\cal X}$
be an effective divisor on
![]() ${\cal X}$
. For its strict transform on
${\cal X}$
. For its strict transform on
![]() ${\cal X}^+$
, we have the equality
${\cal X}^+$
, we have the equality
for some
![]() $\nu \in {\mathbb Z}_+$
. Furthermore, we denote the strict transform of
$\nu \in {\mathbb Z}_+$
. Furthermore, we denote the strict transform of
![]() $D^+_{\cal X}$
on
$D^+_{\cal X}$
on
![]() ${\cal X}_p$
by the symbol
${\cal X}_p$
by the symbol
![]() $D^{(p)}_{\cal X}$
and set
$D^{(p)}_{\cal X}$
and set
Set also
![]() $\mu =\mathop {\mathrm {mult}}_LD^+_{\cal X}$
; obviously,
$\mu =\mathop {\mathrm {mult}}_LD^+_{\cal X}$
; obviously,
![]() $\mu \leqslant \mu _p$
.
$\mu \leqslant \mu _p$
.
Theorem 6.1. The following inequality holds:
Proof. Let
![]() $P\subset E_{\cal Y}$
be a general linear subspace of dimension
$P\subset E_{\cal Y}$
be a general linear subspace of dimension
![]() $(k+2)$
, containing the line L.
$(k+2)$
, containing the line L.
Lemma 6.2. The surface
![]() $S=P\cap {\cal X}^+=P\cap E_{\cal X}$
is non-singular.
$S=P\cap {\cal X}^+=P\cap E_{\cal X}$
is non-singular.
Proof. We argue by induction on
![]() $\mathop {\mathrm {dim}}E_{\cal X}\geqslant 2$
. If
$\mathop {\mathrm {dim}}E_{\cal X}\geqslant 2$
. If
![]() $\mathop {\mathrm {dim}}E_{\cal X}=2$
, then there is nothing to prove. Let
$\mathop {\mathrm {dim}}E_{\cal X}=2$
, then there is nothing to prove. Let
![]() $\mathop {\mathrm {dim}}E_{\cal X}\geqslant 3$
. The hyperplanes in
$\mathop {\mathrm {dim}}E_{\cal X}\geqslant 3$
. The hyperplanes in
![]() $E_{\cal Y}$
, tangent to
$E_{\cal Y}$
, tangent to
![]() $E_{\cal X}$
at at least one point of the line L, form a k-dimensional family. The hyperplanes, containing the line L, form a family (a linear subspace) of codimension 2 in the dual projective space for
$E_{\cal X}$
at at least one point of the line L, form a k-dimensional family. The hyperplanes, containing the line L, form a family (a linear subspace) of codimension 2 in the dual projective space for
![]() $E_{\cal Y}$
– that is, of dimension
$E_{\cal Y}$
– that is, of dimension
![]() $k+\mathop {\mathrm {dim}}E_{\cal X}-2\geqslant k+1$
– so that for a general hyperplane
$k+\mathop {\mathrm {dim}}E_{\cal X}-2\geqslant k+1$
– so that for a general hyperplane
![]() $R_{\cal Y}\supset L$
in
$R_{\cal Y}\supset L$
in
![]() $E_{\cal Y}$
, we have the following:
$E_{\cal Y}$
, we have the following:
![]() $E_{\cal X}\cap R_{\cal Y}$
is non-singular along L (and, of course, for the codimension of the singular set, we have the equality
$E_{\cal X}\cap R_{\cal Y}$
is non-singular along L (and, of course, for the codimension of the singular set, we have the equality
![]() $\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}(E_{\cal X}\cap R_{\cal Y})\subset (E_{\cal X}\cap R_{\cal Y}))=\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}E_{\cal X}\subset E_{\cal X}$
)). Applying the induction hypothesis, we complete the proof of the lemma. Q.E.D.
$\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}(E_{\cal X}\cap R_{\cal Y})\subset (E_{\cal X}\cap R_{\cal Y}))=\mathop {\mathrm {codim}}(\mathop {\mathrm {Sing}}E_{\cal X}\subset E_{\cal X}$
)). Applying the induction hypothesis, we complete the proof of the lemma. Q.E.D.
Let
![]() ${\cal Z}\subset {\cal Y}$
,
${\cal Z}\subset {\cal Y}$
,
![]() ${\cal Z}\ni o$
, be a general subvariety of dimension
${\cal Z}\ni o$
, be a general subvariety of dimension
![]() $(k+3)$
, non-singular at the point o, such that
$(k+3)$
, non-singular at the point o, such that
![]() ${\cal Z}^+\cap E_{\cal Y}=P$
, and
${\cal Z}^+\cap E_{\cal Y}=P$
, and
(the notation
![]() ${\cal X}_P$
is chosen for convenience:
${\cal X}_P$
is chosen for convenience:
![]() ${\cal X}_P$
is determined by
${\cal X}_P$
is determined by
![]() ${\cal Z}$
, not by P). Then
${\cal Z}$
, not by P). Then
![]() ${\cal X}_P$
is a three-dimensional variety with the isolated multi-quadratic singularity
${\cal X}_P$
is a three-dimensional variety with the isolated multi-quadratic singularity
![]() $o\in {\cal X}_P$
, and the blow-up of the point o resolves this singularity: the exceptional divisor
$o\in {\cal X}_P$
, and the blow-up of the point o resolves this singularity: the exceptional divisor
![]() ${\cal X}^+_P\cap E_{\cal Y}$
is the non-singular surface S.
${\cal X}^+_P\cap E_{\cal Y}$
is the non-singular surface S.
The restriction of the divisor
![]() $D_{\cal X}$
onto
$D_{\cal X}$
onto
![]() ${\cal X}_P$
is denoted by the symbol
${\cal X}_P$
is denoted by the symbol
![]() $D_P$
, and its strict transform on
$D_P$
, and its strict transform on
![]() ${\cal X}^+_P$
by the symbol
${\cal X}^+_P$
by the symbol
![]() $D^+_P$
.
$D^+_P$
.
Lemma 6.3. The normal sheaf
![]() ${\cal N}_{L/{\cal X}^+_P}\cong {\cal O}_L(-\alpha )\oplus {\cal O}_L(-\beta )$
, where
${\cal N}_{L/{\cal X}^+_P}\cong {\cal O}_L(-\alpha )\oplus {\cal O}_L(-\beta )$
, where
![]() $\alpha +\beta =k$
and
$\alpha +\beta =k$
and
![]() $\alpha \geqslant \beta \geqslant 1$
.
$\alpha \geqslant \beta \geqslant 1$
.
Proof. Since
![]() $P\cong {\mathbb P}^{k+2}$
, by the adjunction formula
$P\cong {\mathbb P}^{k+2}$
, by the adjunction formula
![]() $K_S=(k-3)H_{S}$
, where
$K_S=(k-3)H_{S}$
, where
![]() $H_S$
is the class of a hyperplane section of
$H_S$
is the class of a hyperplane section of
![]() $S\subset P$
, whence it follows that
$S\subset P$
, whence it follows that
![]() $(L^2)_{S}=1-k$
. Furthermore, the surface S is the exceptional divisor of the blow-up of the point o on
$(L^2)_{S}=1-k$
. Furthermore, the surface S is the exceptional divisor of the blow-up of the point o on
![]() ${\cal X}_P$
(
${\cal X}_P$
(
![]() $S={\cal X}^+_P\cap E_{\cal Y}$
), so that
$S={\cal X}^+_P\cap E_{\cal Y}$
), so that
![]() ${\cal O}_{{\cal X}^+_P}(S)|_L={\cal O}_L(-1)$
, and we have the exact sequence
${\cal O}_{{\cal X}^+_P}(S)|_L={\cal O}_L(-1)$
, and we have the exact sequence
or
From this, the claim of the lemma follows at once. Q.E.D.
Let
![]() $\sigma _L\colon {\cal X}_{P,L}\to {\cal X}^+_P$
be the blow-up of the line L, and
$\sigma _L\colon {\cal X}_{P,L}\to {\cal X}^+_P$
be the blow-up of the line L, and
![]() $E_{P,L}\subset {\cal X}_{P,L}$
the exceptional divisor. The lemma implies that
$E_{P,L}\subset {\cal X}_{P,L}$
the exceptional divisor. The lemma implies that
![]() $E_{P,L}$
is a ruled surface of type
$E_{P,L}$
is a ruled surface of type
![]() ${\mathbb F}_{\alpha -\beta }$
and its Picard group is
${\mathbb F}_{\alpha -\beta }$
and its Picard group is
![]() ${\mathbb Z}s\oplus {\mathbb Z}f$
, where f is the class of a fibre, s the class of the exceptional section,
${\mathbb Z}s\oplus {\mathbb Z}f$
, where f is the class of a fibre, s the class of the exceptional section,
![]() $s^2=-(\alpha -\beta )$
. Again, from the lemma shown above, it follows that
$s^2=-(\alpha -\beta )$
. Again, from the lemma shown above, it follows that
so that
Obviously (since the subspace P is general),
Let
![]() ${\cal X}^{(p)}_P\subset {\cal X}_p$
be the strict transform of
${\cal X}^{(p)}_P\subset {\cal X}_p$
be the strict transform of
![]() ${\cal X}^+_P$
on
${\cal X}^+_P$
on
![]() ${\cal X}_p$
. By construction,
${\cal X}_p$
. By construction,
![]() $q\in {\cal X}^{(p)}_P$
. Setting
$q\in {\cal X}^{(p)}_P$
. Setting
![]() ${D^{(p)}_P=D^{(p)}_{\cal X}|_{{\cal X}^{(p)}_P}}$
, we obtain
${D^{(p)}_P=D^{(p)}_{\cal X}|_{{\cal X}^{(p)}_P}}$
, we obtain
Finally, let
![]() $D^{(L)}_P$
be the strict transform of the divisor
$D^{(L)}_P$
be the strict transform of the divisor
![]() $D^+_P$
on
$D^+_P$
on
![]() ${\cal X}_{P,L}$
. Obviously,
${\cal X}_{P,L}$
. Obviously,
so that, writing the pullback on
![]() ${\cal X}_{P,L}$
of the restriction
${\cal X}_{P,L}$
of the restriction
![]() $E_{\cal X}|_{{\cal X}^+_P}$
for simplicity as the restriction
$E_{\cal X}|_{{\cal X}^+_P}$
for simplicity as the restriction
![]() $E_{\cal X}|_{{\cal X}_{P,L}}$
, we have
$E_{\cal X}|_{{\cal X}_{P,L}}$
, we have
By Proposition 6.2, this effective divisor contains the fibre
![]() $\sigma ^{-1}_L(p)$
with multiplicity at least
$\sigma ^{-1}_L(p)$
with multiplicity at least
![]() $\mu _p+\mu _q-2\mu $
, whence we get the inequality
$\mu _p+\mu _q-2\mu $
, whence we get the inequality
which after easy transformations gives us that
The denominator of the right-hand side is maximal when
![]() $\alpha =k-1$
and
$\alpha =k-1$
and
![]() $\beta =1$
and so
$\beta =1$
and so
Q.E.D. for the theorem.
Proposition 5.3 follows immediately from the theorem that we have just shown, taking into account the construction of the line L and the inequality (18).
7 Hypertangent divisors
In this section, we prove Theorems 1.2, 1.3 and 1.4.
7.1 Non-singular points. Tangent divisors
Let us start the proof of Theorem 1.2. Obviously, it is sufficient to consider the case when the subspace P is of maximal admissible codimension
![]() $k+\varepsilon (k)-1$
in
$k+\varepsilon (k)-1$
in
![]() ${\mathbb P}^{M+k}$
. Theorem 1.1 and Remark 1.4 imply that the inequality
${\mathbb P}^{M+k}$
. Theorem 1.1 and Remark 1.4 imply that the inequality
holds. In particular,
![]() $F\cap P$
is a factorial complete intersection of codimension k in
$F\cap P$
is a factorial complete intersection of codimension k in
![]() ${\mathbb P}\cong {\mathbb P}^{M-\varepsilon (k)+1}$
. Moreover, by the Lefschetz theorem, applied to the section of the variety
${\mathbb P}\cong {\mathbb P}^{M-\varepsilon (k)+1}$
. Moreover, by the Lefschetz theorem, applied to the section of the variety
![]() $F\cap P$
by a general linear subspace of dimension
$F\cap P$
by a general linear subspace of dimension
![]() $3k+1$
in P (this section is a non-singular complete intersection of codimension k in
$3k+1$
in P (this section is a non-singular complete intersection of codimension k in
![]() ${\mathbb P}^{3k+1}$
), we get that the section of
${\mathbb P}^{3k+1}$
), we get that the section of
![]() $F\cap P$
by an arbitrary linear subspace of codimension
$F\cap P$
by an arbitrary linear subspace of codimension
![]() $a\leqslant k$
is irreducible and reduced, since for the numerical Chow group, we have
$a\leqslant k$
is irreducible and reduced, since for the numerical Chow group, we have
where
![]() $H_{F\cap P}$
is the class of a hyperplane section.
$H_{F\cap P}$
is the class of a hyperplane section.
Assume that Theorem 1.2 is not true and
![]() $\mathop {\mathrm {mult}_{\mathrm {o}}}Y>2n(Y)$
. We will argue precisely as in [Reference Pukhlikov26, §2]; see also [Reference Pukhlikov20, Chapter 3, Section 2.1]. Let
$\mathop {\mathrm {mult}_{\mathrm {o}}}Y>2n(Y)$
. We will argue precisely as in [Reference Pukhlikov26, §2]; see also [Reference Pukhlikov20, Chapter 3, Section 2.1]. Let
![]() $T_1,\dots ,T_k$
be the tangent hyperplane sections of
$T_1,\dots ,T_k$
be the tangent hyperplane sections of
![]() $F\cap P$
at the point o (in the notations of Subsection 1.4 they are defined by the linear forms
$F\cap P$
at the point o (in the notations of Subsection 1.4 they are defined by the linear forms
![]() $f_{i,1}|_P$
,
$f_{i,1}|_P$
,
![]() $i=1,\dots ,k$
). By what was said above, for each
$i=1,\dots ,k$
). By what was said above, for each
![]() $i=1,\dots ,k$
, the intersection
$i=1,\dots ,k$
, the intersection
![]() $T_1\cap \dots \cap T_i$
is of codimension i in
$T_1\cap \dots \cap T_i$
is of codimension i in
![]() $F\cap P$
and coincides with the scheme-theoretic intersection
$F\cap P$
and coincides with the scheme-theoretic intersection
![]() $(T_1\circ \dots \circ T_i)$
and its multiplicity at the point o equals precisely
$(T_1\circ \dots \circ T_i)$
and its multiplicity at the point o equals precisely
![]() $2^i$
, since the quadratic forms
$2^i$
, since the quadratic forms
satisfy the regularity condition. Now we argue as in [Reference Pukhlikov26, §2]. We set
![]() $Y_1=Y$
and see that
$Y_1=Y$
and see that
![]() $Y_1\neq T_1$
because
$Y_1\neq T_1$
because
![]() $\mathop {\mathrm {mult}}_oT_1=2n(T_1)=2$
. We consider the cycle
$\mathop {\mathrm {mult}}_oT_1=2n(T_1)=2$
. We consider the cycle
![]() $(Y_1\circ T_1)$
of the scheme-theoretic intersection and take for
$(Y_1\circ T_1)$
of the scheme-theoretic intersection and take for
![]() $Y_2$
the component of that cycle that has the maximal value of the ratio
$Y_2$
the component of that cycle that has the maximal value of the ratio
![]() $\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Assume that the subvariety
$\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Assume that the subvariety
![]() $Y_i$
of codimension i in
$Y_i$
of codimension i in
![]() $F\cap P$
, satisfying the inequality
$F\cap P$
, satisfying the inequality
 $$ \begin{align*}\mathop{\mathrm{mult}}\nolimits_oY_i>\frac{2^i}{\mathop{\mathrm{deg}F}}\mathop{\mathrm{deg}}Y_i \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{mult}}\nolimits_oY_i>\frac{2^i}{\mathop{\mathrm{deg}F}}\mathop{\mathrm{deg}}Y_i \end{align*} $$
is already constructed, and
![]() $i\leqslant k-1$
. Then
$i\leqslant k-1$
. Then
However, by construction,
![]() $Y_i$
is contained in the divisors
$Y_i$
is contained in the divisors
![]() $T_1,\dots ,T_{i-1}$
, so that
$T_1,\dots ,T_{i-1}$
, so that
![]() $Y_i\not \subset T_i$
, and the cycle of scheme-theoretic intersection
$Y_i\not \subset T_i$
, and the cycle of scheme-theoretic intersection
![]() $(Y_i\circ T_i)$
of codimension
$(Y_i\circ T_i)$
of codimension
![]() $i+1$
is well defined. For
$i+1$
is well defined. For
![]() $Y_{i+1}$
, we take the component of this cycle with the maximal value of the ratio
$Y_{i+1}$
, we take the component of this cycle with the maximal value of the ratio
![]() $\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Completing this process, we obtain an irreducible subvariety
$\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Completing this process, we obtain an irreducible subvariety
![]() $Y_{k+1}\subset (F\cap P)$
of codimension
$Y_{k+1}\subset (F\cap P)$
of codimension
![]() $k+1$
, satisfying the inequality
$k+1$
, satisfying the inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}} Y_{k+1}>\frac{2^{k+1}}{\mathop{\mathrm{deg}}F}. \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}} Y_{k+1}>\frac{2^{k+1}}{\mathop{\mathrm{deg}}F}. \end{align*} $$
7.2 Non-singular points. Hypertangent divisors
We continue the proof of Theorem 1.2. In the notations of Subsection 1.4 for each
![]() $j=2,\dots , d_k-1$
, construct the hypertangent linear systems
$j=2,\dots , d_k-1$
, construct the hypertangent linear systems
 $$ \begin{align*}\Lambda_j=\left|\sum^k_{i=1}\sum^{\min\{j,d_i-1\}}_{\alpha=1} f_{i,[1,\alpha]}s_{i,j-\alpha}\right|_{F\cap P}, \end{align*} $$
$$ \begin{align*}\Lambda_j=\left|\sum^k_{i=1}\sum^{\min\{j,d_i-1\}}_{\alpha=1} f_{i,[1,\alpha]}s_{i,j-\alpha}\right|_{F\cap P}, \end{align*} $$
where
![]() $f_{i,[1,\alpha ]}=f_{i,1}+\dots +f_{i,\alpha }$
is the left segment of the polynomial
$f_{i,[1,\alpha ]}=f_{i,1}+\dots +f_{i,\alpha }$
is the left segment of the polynomial
![]() $f_i$
of length
$f_i$
of length
![]() $\alpha $
, the polynomials
$\alpha $
, the polynomials
![]() $s_{i,j-\alpha }$
are homogeneous polynomials of degree
$s_{i,j-\alpha }$
are homogeneous polynomials of degree
![]() $j-\alpha $
, running through the spaces
$j-\alpha $
, running through the spaces
![]() ${\cal P}_{j-\alpha ,M+k}$
independently of each other and the restriction onto
${\cal P}_{j-\alpha ,M+k}$
independently of each other and the restriction onto
![]() $F\cap P$
means the restriction onto the affine part of that variety in
$F\cap P$
means the restriction onto the affine part of that variety in
![]() ${\mathbb A}^{M+k}_{z_*}$
followed by the closure.
${\mathbb A}^{M+k}_{z_*}$
followed by the closure.
Let
![]() $h_a$
, where
$h_a$
, where
![]() $a\geqslant k+1$
, be the a-th polynomial in the sequence
$a\geqslant k+1$
, be the a-th polynomial in the sequence
![]() ${\cal S}$
. Then
${\cal S}$
. Then
![]() $h_a=f_{i,j}|_{{\mathbb P}(T_oF)}$
for some i and
$h_a=f_{i,j}|_{{\mathbb P}(T_oF)}$
for some i and
![]() $j\geqslant 3$
. Set
$j\geqslant 3$
. Set
![]() ${\cal H}_a=\Lambda _{j-1}$
. In this way, we obtain a sequence of linear systems
${\cal H}_a=\Lambda _{j-1}$
. In this way, we obtain a sequence of linear systems
![]() ${\cal H}_{k+1}$
,
${\cal H}_{k+1}$
,
![]() ${\cal H}_{k+2}$
,…,
${\cal H}_{k+2}$
,…,
![]() ${\cal H}_{M}$
, where the system
${\cal H}_{M}$
, where the system
![]() $\Lambda _j$
occurs, in the notations of [Reference Pukhlikov26, §2],
$\Lambda _j$
occurs, in the notations of [Reference Pukhlikov26, §2],
times. By the symbol
![]() ${\cal H}[-m]$
we denote the space
${\cal H}[-m]$
we denote the space
 $$ \begin{align*}\prod^{M-m}_{a=k+1}{\cal H}_a \end{align*} $$
$$ \begin{align*}\prod^{M-m}_{a=k+1}{\cal H}_a \end{align*} $$
of all tuples
![]() $(D_{k+1},\dots ,D_{M-m})$
of divisors, where
$(D_{k+1},\dots ,D_{M-m})$
of divisors, where
![]() $D_a\in {\cal H}_a$
. For
$D_a\in {\cal H}_a$
. For
![]() $a\in \{k+1,\dots ,M\}$
set
$a\in \{k+1,\dots ,M\}$
set
if
![]() ${\cal H}_a=\Lambda _j$
. The number
${\cal H}_a=\Lambda _j$
. The number
![]() $\beta _a$
is called the slope of the divisor
$\beta _a$
is called the slope of the divisor
![]() $D_a$
. It is easy to see that
$D_a$
. It is easy to see that
 $$ \begin{align} \prod^M_{a=k+1}\beta_a=\frac{d_1\dots d_k}{2^k}=\frac{\mathop{\mathrm{deg}} F}{2^k}. \end{align} $$
$$ \begin{align} \prod^M_{a=k+1}\beta_a=\frac{d_1\dots d_k}{2^k}=\frac{\mathop{\mathrm{deg}} F}{2^k}. \end{align} $$
Set
![]() $m_*=k+\varepsilon (k)+3$
. Let
$m_*=k+\varepsilon (k)+3$
. Let
be a general tuple. The technique of hypertangent divisors, applied in precisely the same way as in [Reference Pukhlikov26, §2] or [Reference Pukhlikov20, Chapter 3, Subsection 2.2] – see also [Reference Pukhlikov2, Proposition 2.1] – gives the following claim.
Proposition 7.1. There is a sequence of irreducible subvarieties
where
![]() $Y_{k+1}$
has been constructed above, such that
$Y_{k+1}$
has been constructed above, such that
![]() $\mathop {\mathrm { codim}}(Y_i\subset (F\cap P))=i$
, the subvariety
$\mathop {\mathrm { codim}}(Y_i\subset (F\cap P))=i$
, the subvariety
![]() $Y_i$
is not contained in the support of the divisor
$Y_i$
is not contained in the support of the divisor
![]() $D_{i+1}$
for
$D_{i+1}$
for
![]() $i\leqslant M-m_*-1$
, the subvariety
$i\leqslant M-m_*-1$
, the subvariety
![]() $Y_{i+1}$
is an irreducible component of the effective cycle
$Y_{i+1}$
is an irreducible component of the effective cycle
![]() $(Y_i\circ D_{i+1})$
and the following inequality holds:
$(Y_i\circ D_{i+1})$
and the following inequality holds:
There is no need to give a proof of that claim because it is identical to the arguments mentioned above. Note only that the key point in the construction of the sequence of subvarieties
![]() $Y_i$
is the fact that
$Y_i$
is the fact that
![]() $Y_i$
is not contained in the support of a general divisor
$Y_i$
is not contained in the support of a general divisor
![]() $D_{i+1}\in {\cal H}_{i+1}$
, and this fact follows from the regularity condition (R1). Since
$D_{i+1}\in {\cal H}_{i+1}$
, and this fact follows from the regularity condition (R1). Since
![]() $\mathop {\mathrm {dim}}(F\cap P)=M+1-k-\varepsilon (k)$
, the subvariety
$\mathop {\mathrm {dim}}(F\cap P)=M+1-k-\varepsilon (k)$
, the subvariety
![]() $Y^*=Y_{M-m_*}$
is of dimension 4 and satisfies the inequality
$Y^*=Y_{M-m_*}$
is of dimension 4 and satisfies the inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y^*> \frac{\displaystyle\frac{2^{k+1}}{\mathop{\mathrm{ deg}}F}\cdot\frac{\mathop{\mathrm{deg}} F}{2^k}}{\displaystyle\frac32\cdot\prod\limits^M_{a=M-m_*+1}\beta_a}= \frac43\frac{1}{\prod\limits^M_{a=M-m_*+1}\beta_a}. \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y^*> \frac{\displaystyle\frac{2^{k+1}}{\mathop{\mathrm{ deg}}F}\cdot\frac{\mathop{\mathrm{deg}} F}{2^k}}{\displaystyle\frac32\cdot\prod\limits^M_{a=M-m_*+1}\beta_a}= \frac43\frac{1}{\prod\limits^M_{a=M-m_*+1}\beta_a}. \end{align*} $$
(The number
![]() $\frac 32$
appears in the denominator because the hypertangent divisor
$\frac 32$
appears in the denominator because the hypertangent divisor
![]() $D_{k+1}$
is skipped in the procedure of intersection, in the same way and for the same reason as in [Reference Pukhlikov26, §2], and its slope is
$D_{k+1}$
is skipped in the procedure of intersection, in the same way and for the same reason as in [Reference Pukhlikov26, §2], and its slope is
![]() $\frac 32$
.) Now the inequality
$\frac 32$
.) Now the inequality
 $$ \begin{align} \frac43\geqslant\prod^M_{a=M-m_*+1}\beta_a, \end{align} $$
$$ \begin{align} \frac43\geqslant\prod^M_{a=M-m_*+1}\beta_a, \end{align} $$
shown below in Proposition 7.2, completes the proof of Theorem 1.2.
Proposition 7.2. Assume that for
![]() $k=3,4,5$
, the dimension M is, respectively, at least
$k=3,4,5$
, the dimension M is, respectively, at least
![]() $96$
,
$96$
,
![]() $160$
,
$160$
,
![]() $215$
, and for
$215$
, and for
![]() $k\geqslant 6$
, the inequality
$k\geqslant 6$
, the inequality
![]() $M\geqslant 8k^2+2k$
holds. Then the inequality (21) is true.
$M\geqslant 8k^2+2k$
holds. Then the inequality (21) is true.
Proof. Using the obvious fact that the function
![]() $\frac {t+1}{t}$
is decreasing, it is easy to see that the right-hand side of the inequality (21) with k and M fixed attains the maximum when the degrees
$\frac {t+1}{t}$
is decreasing, it is easy to see that the right-hand side of the inequality (21) with k and M fixed attains the maximum when the degrees
![]() $d_1,\dots ,d_k$
are equal or ‘almost equal’ in the following sense: let
$d_1,\dots ,d_k$
are equal or ‘almost equal’ in the following sense: let
![]() $M\equiv e\mathop{\mathrm {mod}}k$
with
$M\equiv e\mathop{\mathrm {mod}}k$
with
![]() $e\in \{0,1,\dots ,k-1\}$
, then the ‘almost equality’ means that
$e\in \{0,1,\dots ,k-1\}$
, then the ‘almost equality’ means that
For
![]() $k\in \{3,\dots ,9\}$
, the claim of the proposition can be checked for each case of almost equal degrees – that is, for each possible value of e – manually, computing
$k\in \{3,\dots ,9\}$
, the claim of the proposition can be checked for each case of almost equal degrees – that is, for each possible value of e – manually, computing
![]() $\varepsilon (k)$
explicitly. For
$\varepsilon (k)$
explicitly. For
![]() $k\geqslant 10$
, it is easy to see that
$k\geqslant 10$
, it is easy to see that
![]() $\varepsilon (k)\leqslant k-3$
, so that
$\varepsilon (k)\leqslant k-3$
, so that
![]() $m_*\leqslant 2k$
. Therefore (again considering the case of almost equal degrees), the right-hand side of (21) does not exceed the number
$m_*\leqslant 2k$
. Therefore (again considering the case of almost equal degrees), the right-hand side of (21) does not exceed the number
 $$ \begin{align*}\left(\frac{\frac{M}{k}}{\frac{M}{k}-2}\right)^k= \left(\frac{M}{M-2k}\right)^k, \end{align*} $$
$$ \begin{align*}\left(\frac{\frac{M}{k}}{\frac{M}{k}-2}\right)^k= \left(\frac{M}{M-2k}\right)^k, \end{align*} $$
from which we get that (21) is true if
 $$ \begin{align*}M\geqslant 2k\frac{(1+\frac13)^{\frac{1}{k}}}{(1+\frac13)^{\frac{1}{k}}-1}. \end{align*} $$
$$ \begin{align*}M\geqslant 2k\frac{(1+\frac13)^{\frac{1}{k}}}{(1+\frac13)^{\frac{1}{k}}-1}. \end{align*} $$
If in the numerator and denominator we replace
![]() $(1+\frac {1}{3})^{\frac {1}{k}}$
by the smaller number
$(1+\frac {1}{3})^{\frac {1}{k}}$
by the smaller number
![]() $1+\frac {1}{4k}$
, the right-hand side of the last inequality gets higher. This proves the proposition. Q.E.D.
$1+\frac {1}{4k}$
, the right-hand side of the last inequality gets higher. This proves the proposition. Q.E.D.
Note that for
![]() $M\geqslant \rho (k)$
(see the inequality (1) in Subsection 0.1), the assumptions of the previous proposition are satisfied. This completes the proof of Theorem 1.2.
$M\geqslant \rho (k)$
(see the inequality (1) in Subsection 0.1), the assumptions of the previous proposition are satisfied. This completes the proof of Theorem 1.2.
7.3 Quadratic points
Let us show Theorem 1.3. Note first of all that if Y is a section of the variety W by a hyperplane that is tangent to W at the point o (that is, the equation of the hyperplane is a linear combination of the forms
![]() $f_{1,1},\dots ,f_{k,1}$
, restricted onto the hyperplane
$f_{1,1},\dots ,f_{k,1}$
, restricted onto the hyperplane
![]() ${\mathbb P}(W)\cong {\mathbb P}^{M+k-1}$
), then
${\mathbb P}(W)\cong {\mathbb P}^{M+k-1}$
), then
so that the claim of the theorem is optimal. Thus, we assume the converse: the inequality
holds. We argue as in the non-singular case (Subsection 7.1): let
![]() $T_1,\dots ,T_{k-1}$
be the tangent hyperplane sections, given by
$T_1,\dots ,T_{k-1}$
be the tangent hyperplane sections, given by
![]() $(k-1)$
independent forms taken from the set
$(k-1)$
independent forms taken from the set
![]() $\{f_{1,1},\dots ,f_{k,1}\}$
. Since
$\{f_{1,1},\dots ,f_{k,1}\}$
. Since
![]() $\mathop {\mathrm {codim}}(\mathop{ \mathrm { Sing}}F\subset F)\geqslant 2k+2$
, all scheme-theoretic intersections
$\mathop {\mathrm {codim}}(\mathop{ \mathrm { Sing}}F\subset F)\geqslant 2k+2$
, all scheme-theoretic intersections
![]() $(T_1\circ \dots \circ T_i)$
,
$(T_1\circ \dots \circ T_i)$
,
![]() $1\leqslant i\leqslant k-1$
, are irreducible, reduced and coincide with the set-theoretic intersection
$1\leqslant i\leqslant k-1$
, are irreducible, reduced and coincide with the set-theoretic intersection
![]() $T_1\cap \dots \cap T_i$
, and moreover, by the condition (R2), the equality
$T_1\cap \dots \cap T_i$
, and moreover, by the condition (R2), the equality
holds. In particular,
![]() $\mathop {\mathrm {mult}}_oT_1=4n(T_1)=4$
, so that
$\mathop {\mathrm {mult}}_oT_1=4n(T_1)=4$
, so that
![]() $Y\neq T_1$
. Arguing as in Subsection 7.1, we construct a sequence of irreducible subvarieties
$Y\neq T_1$
. Arguing as in Subsection 7.1, we construct a sequence of irreducible subvarieties
![]() $Y_1=Y,Y_2,\dots ,Y_k$
, where
$Y_1=Y,Y_2,\dots ,Y_k$
, where
![]() $\mathop {\mathrm {codim}}(Y_i\subset W)=i$
and the inequality
$\mathop {\mathrm {codim}}(Y_i\subset W)=i$
and the inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{ deg}}}Y_k>\frac{2^{k+1}}{\mathop{\mathrm{deg}}F} \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{ deg}}}Y_k>\frac{2^{k+1}}{\mathop{\mathrm{deg}}F} \end{align*} $$
holds. Now the proof of Theorem 1.3 repeats the arguments of Subsection 7.2, where
![]() $m_*$
is replaced by 4. Since
$m_*$
is replaced by 4. Since
![]() $4<m_*$
, the inequality (21) guarantees the inequality which is obtained from (21) when
$4<m_*$
, the inequality (21) guarantees the inequality which is obtained from (21) when
![]() $m_*$
is replaced by 4. This completes the proof of Theorem 1.3.
$m_*$
is replaced by 4. This completes the proof of Theorem 1.3.
7.4 Multi-quadratic points. Tangent divisors
We start the proof of Theorem 1.4, the structure of which is similar to the structure of the proof of Theorem 1.2. At first, we argue as in Subsection 7.1: it is sufficient to consider a linear subspace P in
![]() $T_oF$
of maximal admissible codimension
$T_oF$
of maximal admissible codimension
![]() $\varepsilon (k)$
. Assume that the prime divisor Y on
$\varepsilon (k)$
. Assume that the prime divisor Y on
![]() $F\cap P$
satisfies the inequality
$F\cap P$
satisfies the inequality
or the equivalent inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{ deg}}}Y>\frac32\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}, \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{ deg}}}Y>\frac32\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}, \end{align*} $$
and consider the second hypertangent linear system (which in this case plays the role of the tangent linear system)
 $$ \begin{align*}\Lambda_2=\left|\sum_{d_i\geqslant 3}s_{i,0}f_{i,2}\right|_{F\cap P}, \end{align*} $$
$$ \begin{align*}\Lambda_2=\left|\sum_{d_i\geqslant 3}s_{i,0}f_{i,2}\right|_{F\cap P}, \end{align*} $$
where
![]() $s_{i,0}\in {\mathbb C}$
are constants, independent of each other. Instead of the Lefschetz theorem, we use the condition (R3.1): the system of equations
$s_{i,0}\in {\mathbb C}$
are constants, independent of each other. Instead of the Lefschetz theorem, we use the condition (R3.1): the system of equations
![]() $f_{i,2}|_{F\cap P}=0$
, where
$f_{i,2}|_{F\cap P}=0$
, where
![]() $d_i\geqslant 3$
defines an irreducible reduced subvariety of codimension
$d_i\geqslant 3$
defines an irreducible reduced subvariety of codimension
![]() $k+k_{\geqslant 3}$
in P, and by (R3.2), the multiplicity of that subvariety at the point o is precisely
$k+k_{\geqslant 3}$
in P, and by (R3.2), the multiplicity of that subvariety at the point o is precisely
![]() $2^k\cdot (\frac 32)^{k_{\geqslant 3}}$
. More precisely, for a general tuple
$2^k\cdot (\frac 32)^{k_{\geqslant 3}}$
. More precisely, for a general tuple
![]() $(D_{2,1},\dots ,D_{2,k_{\geqslant 3}})$
of divisors in the system
$(D_{2,1},\dots ,D_{2,k_{\geqslant 3}})$
of divisors in the system
![]() $\Lambda _2$
, the following claim is true: for each
$\Lambda _2$
, the following claim is true: for each
![]() $i=1,\dots ,k_{\geqslant 3}$
, the cycle
$i=1,\dots ,k_{\geqslant 3}$
, the cycle
![]() $(D_{2,1}\circ \dots \circ D_{2,i}$
) of the scheme-theoretic intersection of the divisors
$(D_{2,1}\circ \dots \circ D_{2,i}$
) of the scheme-theoretic intersection of the divisors
![]() $D_{2,1},\dots ,D_{2,i}$
is an irreducible reduced subvariety of codimension i in
$D_{2,1},\dots ,D_{2,i}$
is an irreducible reduced subvariety of codimension i in
![]() $F\cap P$
, the multiplicity of which at the point o is
$F\cap P$
, the multiplicity of which at the point o is
![]() $2^k\cdot (\frac 32)^i$
. Arguing as in Subsection 7.1, we construct a sequence
$2^k\cdot (\frac 32)^i$
. Arguing as in Subsection 7.1, we construct a sequence
![]() $Y_1=Y,Y_2,\dots ,Y_{k_{\geqslant 3}}$
of irreducible subvarieties of codimension
$Y_1=Y,Y_2,\dots ,Y_{k_{\geqslant 3}}$
of irreducible subvarieties of codimension
![]() $\mathop {\mathrm { codim}}(Y_i\subset (F\cap P))=i$
, where
$\mathop {\mathrm { codim}}(Y_i\subset (F\cap P))=i$
, where
![]() $Y_{i+1}$
is an irreducible component of the cycle
$Y_{i+1}$
is an irreducible component of the cycle
![]() $(Y_i\circ D_{2,i})$
with the maximal value of the ratio
$(Y_i\circ D_{2,i})$
with the maximal value of the ratio
![]() $\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Therefore,
$\mathop {\mathrm {mult}}_o/\mathop {\mathrm {deg}}$
. Therefore,
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y_{k_{\geqslant 3}}> \left(\frac32\right)^{k_{\geqslant 3}}\cdot\frac{2^k}{\mathop{\mathrm{ deg}}F}. \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y_{k_{\geqslant 3}}> \left(\frac32\right)^{k_{\geqslant 3}}\cdot\frac{2^k}{\mathop{\mathrm{ deg}}F}. \end{align*} $$
It follows from here that
![]() $Y_{k_{\geqslant 3}}\neq D_{2,1}\cap \dots \cap D_{2,k_{\geqslant 3}}$
, but since by construction,
$Y_{k_{\geqslant 3}}\neq D_{2,1}\cap \dots \cap D_{2,k_{\geqslant 3}}$
, but since by construction,
we conclude that
![]() $Y_{k_{\geqslant 3}}\not \subset D_{2,k_{\geqslant 3}}$
, so that the effective cycle
$Y_{k_{\geqslant 3}}\not \subset D_{2,k_{\geqslant 3}}$
, so that the effective cycle
![]() $(Y_{k_{\geqslant 3}}\circ D_{2,k_{\geqslant 3}})$
of the scheme-theoretic intersection of these varieties is well defined and one of its components
$(Y_{k_{\geqslant 3}}\circ D_{2,k_{\geqslant 3}})$
of the scheme-theoretic intersection of these varieties is well defined and one of its components
![]() $Y_{k_{\geqslant 3}+1}$
satisfies the inequality
$Y_{k_{\geqslant 3}+1}$
satisfies the inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y_{k_{\geqslant 3}+1}> \left(\frac32\right)^{k_{\geqslant 3}+1}\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}. \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y_{k_{\geqslant 3}+1}> \left(\frac32\right)^{k_{\geqslant 3}+1}\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}. \end{align*} $$
7.5 Multi-quadratic points. Hypertangent divisors
Now we argue almost word for word as in Subsection 7.2: construct the hypertangent systems
 $$ \begin{align*}\Lambda_j=\left|\sum^j_{\alpha=2}\sum_{d_i\geqslant \alpha+1}f_{i,[2,\alpha]}s_{i,j-\alpha}\right|_{F\cap P}, \end{align*} $$
$$ \begin{align*}\Lambda_j=\left|\sum^j_{\alpha=2}\sum_{d_i\geqslant \alpha+1}f_{i,[2,\alpha]}s_{i,j-\alpha}\right|_{F\cap P}, \end{align*} $$
where
![]() $j=3,\dots ,d_k-1$
and all symbols have the same meaning as in Subsection 7.2. If
$j=3,\dots ,d_k-1$
and all symbols have the same meaning as in Subsection 7.2. If
![]() $h_a$
, where
$h_a$
, where
![]() $a\geqslant k+k_{\geqslant 3}+1$
is the a-th polynomial in the sequence
$a\geqslant k+k_{\geqslant 3}+1$
is the a-th polynomial in the sequence
![]() ${\cal S},h_a=f_{i,j}|_{{\mathbb P}(T_oF)}$
, for some i and
${\cal S},h_a=f_{i,j}|_{{\mathbb P}(T_oF)}$
, for some i and
![]() $j\geqslant 4$
, then we set
$j\geqslant 4$
, then we set
![]() ${\cal H}_a=\Lambda _{j-1}$
and obtain the sequence of linear systems
${\cal H}_a=\Lambda _{j-1}$
and obtain the sequence of linear systems
By the symbol
![]() ${\cal H}[-m]$
we denote the space
${\cal H}[-m]$
we denote the space
 $$ \begin{align*}\prod^{M-m}_{a=k+k_{\geqslant 3}+1}{\cal H}_a. \end{align*} $$
$$ \begin{align*}\prod^{M-m}_{a=k+k_{\geqslant 3}+1}{\cal H}_a. \end{align*} $$
Instead of the equality (20), we get the equality
 $$ \begin{align*}\prod^M_{a=k+k_{\geqslant 3}+1}\beta_a=\frac{\mathop{\mathrm{ deg}}F}{2^k\left(\frac32\right)^{k_{\geqslant 3}}}. \end{align*} $$
$$ \begin{align*}\prod^M_{a=k+k_{\geqslant 3}+1}\beta_a=\frac{\mathop{\mathrm{ deg}}F}{2^k\left(\frac32\right)^{k_{\geqslant 3}}}. \end{align*} $$
Let
![]() $(D_{k+k_{\geqslant 3}+1},\dots ,D_{M-m^*})\in {\cal H}[-m^*]$
be a general tuple. Now the technique of hypertangent divisors, applied in the word for word the same way as in Subsection 7.2, gives the following claim.
$(D_{k+k_{\geqslant 3}+1},\dots ,D_{M-m^*})\in {\cal H}[-m^*]$
be a general tuple. Now the technique of hypertangent divisors, applied in the word for word the same way as in Subsection 7.2, gives the following claim.
Proposition 7.3. There is a sequence of irreducible subvarieties
where
![]() $Y_{k_{\geqslant 3}+1}$
is constructed above, such that
$Y_{k_{\geqslant 3}+1}$
is constructed above, such that
![]() $\mathop {\mathrm {codim}}(Y_i\subset (F\cap P))=i$
, the subvariety
$\mathop {\mathrm {codim}}(Y_i\subset (F\cap P))=i$
, the subvariety
![]() $Y_i$
is not contained in the support of the divisor
$Y_i$
is not contained in the support of the divisor
![]() $D_{k+i+1}$
for
$D_{k+i+1}$
for
![]() $i\leqslant M-m^*-1$
, the subvariety
$i\leqslant M-m^*-1$
, the subvariety
![]() $Y_{i+1}$
is an irreducible component of the effective cycle
$Y_{i+1}$
is an irreducible component of the effective cycle
![]() $(Y_i\circ D_{k+i+1})$
and the following inequality holds:
$(Y_i\circ D_{k+i+1})$
and the following inequality holds:
Now since
![]() $\mathop {\mathrm {dim}}F\cap P=M-(k-l)-\varepsilon (k)$
, by the definition of the number
$\mathop {\mathrm {dim}}F\cap P=M-(k-l)-\varepsilon (k)$
, by the definition of the number
![]() $m^*$
, the last subvariety
$m^*$
, the last subvariety
![]() $Y^*=Y_{M-k-m^*}$
in that sequence is of dimension
$Y^*=Y_{M-k-m^*}$
in that sequence is of dimension
![]() $\geqslant 4$
and satisfies the inequality
$\geqslant 4$
and satisfies the inequality
 $$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y^*> \frac{ \displaystyle \left(\frac32\right)^{k_{\geqslant 3}+1}\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}\cdot \frac{\mathop{\mathrm{ deg}}F}{2^k \left(\frac32\right)^{k_{\geqslant 3}}}}{\displaystyle \frac43\prod\limits^M_{a=M-m_*+1}\beta_{k+a}}= \frac98\frac{1}{\displaystyle\prod\limits^M_{a=M-m_*+1}\beta_{k+a}}. \end{align*} $$
$$ \begin{align*}\frac{\mathop{\mathrm{mult}}_o}{\mathop{\mathrm{deg}}}Y^*> \frac{ \displaystyle \left(\frac32\right)^{k_{\geqslant 3}+1}\cdot\frac{2^k}{\mathop{\mathrm{deg}}F}\cdot \frac{\mathop{\mathrm{ deg}}F}{2^k \left(\frac32\right)^{k_{\geqslant 3}}}}{\displaystyle \frac43\prod\limits^M_{a=M-m_*+1}\beta_{k+a}}= \frac98\frac{1}{\displaystyle\prod\limits^M_{a=M-m_*+1}\beta_{k+a}}. \end{align*} $$
(The number
![]() $\frac 43$
appears in the denominator of the right-hand side because the hypertangent divisor
$\frac 43$
appears in the denominator of the right-hand side because the hypertangent divisor
![]() $D_{k+k_{\geqslant 3}+1}$
is skipped in the process of constructing the sequence
$D_{k+k_{\geqslant 3}+1}$
is skipped in the process of constructing the sequence
![]() $Y_*$
; see the similar remark above, before the inequality (21).) If
$Y_*$
; see the similar remark above, before the inequality (21).) If
![]() $m^*=0$
, then the product in the denominator is assumed to be equal to 1. Now the inequality
$m^*=0$
, then the product in the denominator is assumed to be equal to 1. Now the inequality
 $$ \begin{align} \frac98\geqslant\prod^M_{a=M-m^*+1}\beta_{k+a}, \end{align} $$
$$ \begin{align} \frac98\geqslant\prod^M_{a=M-m^*+1}\beta_{k+a}, \end{align} $$
shown below in Proposition 7.4, completes the proof of Theorem 1.4.
Proposition 7.4. Assume that for
![]() $k\in \{3,\dots ,7\}$
, the number M is at least the number shown in the corresponding column of the table
$k\in \{3,\dots ,7\}$
, the number M is at least the number shown in the corresponding column of the table

and for
![]() $k\geqslant 8$
, the inequality
$k\geqslant 8$
, the inequality
![]() $M\geqslant 9k^2+k$
holds. Then the inequality (22) holds.
$M\geqslant 9k^2+k$
holds. Then the inequality (22) holds.
Proof. As in the non-singular case (the proof of Proposition 7.2), we see that the right-hand side of the inequality (22) for k and M fixed attains the maximum when the degrees
![]() $d_i$
are equal or ‘almost equal’. For
$d_i$
are equal or ‘almost equal’. For
![]() $k\in \{3,\dots ,7\}$
, the claim of the proposition is checked manually. For
$k\in \{3,\dots ,7\}$
, the claim of the proposition is checked manually. For
![]() $k\geqslant 8$
, we have
$k\geqslant 8$
, we have
![]() $\varepsilon (k)\leqslant k-2$
, so that
$\varepsilon (k)\leqslant k-2$
, so that
![]() $m^*\leqslant k$
. Therefore, (considering the case of equal or almost equal degrees) the right-hand side of the inequality (22) does not exceed the number
$m^*\leqslant k$
. Therefore, (considering the case of equal or almost equal degrees) the right-hand side of the inequality (22) does not exceed the number
 $$ \begin{align*}\left(\frac{M}{M-k}\right)^k, \end{align*} $$
$$ \begin{align*}\left(\frac{M}{M-k}\right)^k, \end{align*} $$
which, in its turn, does not exceed
![]() $\frac 98$
for
$\frac 98$
for
![]() $M\geqslant 9k^2+k$
, which is easy to check by elementary computations, similar to the proof Proposition 7.2. Q.E.D.
$M\geqslant 9k^2+k$
, which is easy to check by elementary computations, similar to the proof Proposition 7.2. Q.E.D.
8 The codimension of the complement
In this section, we show the estimate for the codimension of the complement
![]() ${\cal P}\setminus {\cal F}$
, given in Theorem 0.1.
${\cal P}\setminus {\cal F}$
, given in Theorem 0.1.
8.1 Preliminary constructions
Set
 $$ \begin{align*}\gamma=M-k+5+{M-\rho(k)+2\choose 2}; \end{align*} $$
$$ \begin{align*}\gamma=M-k+5+{M-\rho(k)+2\choose 2}; \end{align*} $$
see Subsection 0.1. We consider
![]() $\gamma $
as a function of M with
$\gamma $
as a function of M with
![]() $k\geqslant 3$
fixed, where
$k\geqslant 3$
fixed, where
![]() $M\geqslant \rho (k)$
. Let
$M\geqslant \rho (k)$
. Let
![]() $o\in {\mathbb P}^{M+k}$
be an arbitrary point. The symbol
$o\in {\mathbb P}^{M+k}$
be an arbitrary point. The symbol
![]() ${\cal P}(o)$
stands for the linear subspace of the space
${\cal P}(o)$
stands for the linear subspace of the space
![]() ${\cal P}$
, consisting of all tuples
${\cal P}$
, consisting of all tuples
![]() $\underline {f}$
, vanishing at the point o:
$\underline {f}$
, vanishing at the point o:
![]() $\underline {f}(o)=(0,\dots ,0)$
. Obviously,
$\underline {f}(o)=(0,\dots ,0)$
. Obviously,
![]() $\mathop {\mathrm { codim}}({\cal P}(o)\subset {\cal P})=k$
. Fixing the point o, we use the notations of Subsections 1.2–1.4, considering the polynomials
$\mathop {\mathrm { codim}}({\cal P}(o)\subset {\cal P})=k$
. Fixing the point o, we use the notations of Subsections 1.2–1.4, considering the polynomials
![]() $f_i$
as non-homogeneous polynomials in the affine coordinates
$f_i$
as non-homogeneous polynomials in the affine coordinates
![]() $z_*$
. By the symbols
$z_*$
. By the symbols
we denote the subsets of the subspace
![]() ${\cal P}(o)$
, consisting of the tuples
${\cal P}(o)$
, consisting of the tuples
![]() $\underline {f}$
that do not satisfy the conditions
$\underline {f}$
that do not satisfy the conditions
at the point o, respectively. Since the point o varies in
![]() ${\mathbb P}^{M+k}$
, it is sufficient to show that the codimension of each of the six sets
${\mathbb P}^{M+k}$
, it is sufficient to show that the codimension of each of the six sets
![]() ${\cal B}_*$
in
${\cal B}_*$
in
![]() ${\cal P}(o)$
is at least
${\cal P}(o)$
is at least
![]() $\gamma +M$
.
$\gamma +M$
.
Furthermore, for an arbitrary tuple
of linear forms in
![]() $z_*$
, the symbol
$z_*$
, the symbol
![]() ${\cal P}(o,\underline {\xi })$
denotes the affine subspace, consisting of the tuples
${\cal P}(o,\underline {\xi })$
denotes the affine subspace, consisting of the tuples
![]() $\underline {f}$
, such that
$\underline {f}$
, such that
By the symbol
![]() $\mathop {\mathrm {dim}}\underline {\xi }$
denote the dimension
$\mathop {\mathrm {dim}}\underline {\xi }$
denote the dimension
so that
![]() ${\cal P}(o)$
is fibred into disjoint subsets
${\cal P}(o)$
is fibred into disjoint subsets
 $$ \begin{align*}{\cal P}^{(i)}(o)=\bigcup_{\mathop{\mathrm{dim}}\underline{\xi}=i}{\cal P}(o,\underline{\xi}), \end{align*} $$
$$ \begin{align*}{\cal P}^{(i)}(o)=\bigcup_{\mathop{\mathrm{dim}}\underline{\xi}=i}{\cal P}(o,\underline{\xi}), \end{align*} $$
where
![]() $i=0,1,\dots ,k$
. Obviously, the equality
$i=0,1,\dots ,k$
. Obviously, the equality
holds. In particular,
![]() ${\cal P}^{(k)}(o)$
consists of the tuples
${\cal P}^{(k)}(o)$
consists of the tuples
![]() $\underline {f}$
, such that the scheme of their common zeros is a non-singular subvariety of codimension k in a neighborhood of the point o. Set
$\underline {f}$
, such that the scheme of their common zeros is a non-singular subvariety of codimension k in a neighborhood of the point o. Set
For the case of a non-singular point, it is sufficient to prove the inequality
where
![]() $\mathop {\mathrm {dim}}\underline {\xi }=k$
.
$\mathop {\mathrm {dim}}\underline {\xi }=k$
.
Furthermore, let
![]() ${\cal B}_{MQ1}(\underline {\xi })={\cal B}_{MQ1}\cap {\cal P} (o,{\underline {\xi }})$
, where
${\cal B}_{MQ1}(\underline {\xi })={\cal B}_{MQ1}\cap {\cal P} (o,{\underline {\xi }})$
, where
![]() $\mathop {\mathrm { dim}}\underline {\xi }=i\leqslant k-1$
, be the set of the tuples
$\mathop {\mathrm { dim}}\underline {\xi }=i\leqslant k-1$
, be the set of the tuples
![]() $\underline {f}$
, such that the condition (MQ1) for
$\underline {f}$
, such that the condition (MQ1) for
![]() $l=k-i$
is not satisfied, and
$l=k-i$
is not satisfied, and
![]() ${\cal B}_{MQ2}(\underline {\xi })={\cal B}_{MQ2}\cap {\cal P }(o,\underline {\xi })$
, where
${\cal B}_{MQ2}(\underline {\xi })={\cal B}_{MQ2}\cap {\cal P }(o,\underline {\xi })$
, where
![]() $\mathop {\mathrm { dim}}\underline {\xi }=i\leqslant k-2$
, be the set of the tuples
$\mathop {\mathrm { dim}}\underline {\xi }=i\leqslant k-2$
, be the set of the tuples
![]() $\underline {f}$
, such that the condition (MQ2) for
$\underline {f}$
, such that the condition (MQ2) for
![]() $l=k-i$
is not satisfied.
$l=k-i$
is not satisfied.
In a similar way, we define the sets
![]() ${\cal B}_{R2}(\underline {\xi })$
for
${\cal B}_{R2}(\underline {\xi })$
for
![]() $\mathop {\mathrm { dim}}\underline {\xi }=k-1$
and
$\mathop {\mathrm { dim}}\underline {\xi }=k-1$
and
![]() ${\cal B}_{R3.1}(\underline {\xi })$
,
${\cal B}_{R3.1}(\underline {\xi })$
,
![]() ${\cal B}_{R3.2}(\underline {\xi })$
for
${\cal B}_{R3.2}(\underline {\xi })$
for
![]() $\mathop {\mathrm { dim}}\underline {\xi }\leqslant k-2$
.
$\mathop {\mathrm { dim}}\underline {\xi }\leqslant k-2$
.
Clearly, it is sufficient to prove that for
![]() $\mathop {\mathrm { dim}}\underline {\xi }=i$
, the codimension of the set
$\mathop {\mathrm { dim}}\underline {\xi }=i$
, the codimension of the set
![]() ${\cal B}_*(\underline {\xi })$
in
${\cal B}_*(\underline {\xi })$
in
![]() ${\cal P}(o,\underline {\xi })$
is at least
${\cal P}(o,\underline {\xi })$
is at least
In the conditions (R1), (R2) and (R3.2), we have also an arbitrary subspace
![]() $\Pi \subset {\mathbb P}(T_oF)$
of the corresponding codimension, and in the condition (R3.1) an arbitrary subspace P in the embedded tangent space
$\Pi \subset {\mathbb P}(T_oF)$
of the corresponding codimension, and in the condition (R3.1) an arbitrary subspace P in the embedded tangent space
![]() $T_oF\subset {\mathbb P}^{M+k}$
of codimension
$T_oF\subset {\mathbb P}^{M+k}$
of codimension
![]() $\varepsilon (k)$
, containing the point o. For an arbitrary subspace
$\varepsilon (k)$
, containing the point o. For an arbitrary subspace
![]() $\Pi \subset {\mathbb P}(T_oF)$
of the corresponding codimension, let
$\Pi \subset {\mathbb P}(T_oF)$
of the corresponding codimension, let
be the set of tuples
![]() $\underline {f}\in {\cal P}(o,\underline {\xi })$
, such that the respective condition (R1), (R2) and (R3.2) is violated precisely for that subspace
$\underline {f}\in {\cal P}(o,\underline {\xi })$
, such that the respective condition (R1), (R2) and (R3.2) is violated precisely for that subspace
![]() $\Pi $
. In a similar way, we define the subset
$\Pi $
. In a similar way, we define the subset
![]() ${\cal B}_{R3.1}(\underline {\xi },P)$
. These definitions are meaningful because the tangent space
${\cal B}_{R3.1}(\underline {\xi },P)$
. These definitions are meaningful because the tangent space
![]() $T_oF$
is given by the fixed linear forms
$T_oF$
is given by the fixed linear forms
![]() $\xi _i$
and for that reason is fixed.
$\xi _i$
and for that reason is fixed.
Since the subspace
![]() $\Pi $
varies in a
$\Pi $
varies in a
![]() $(\mathop {\mathrm { dim}}\Pi +1)\mathop {\mathrm {codim}}(\Pi \subset {\mathbb P}(T_oF))$
-dimensional Grassmanian, the estimate for the codimension of the set
$(\mathop {\mathrm { dim}}\Pi +1)\mathop {\mathrm {codim}}(\Pi \subset {\mathbb P}(T_oF))$
-dimensional Grassmanian, the estimate for the codimension of the set
![]() ${\cal B}_*(\underline {\xi },\Pi )$
in
${\cal B}_*(\underline {\xi },\Pi )$
in
![]() ${\cal P}(o,\underline {\xi })$
should be stronger than the estimate for the codimension of the set
${\cal P}(o,\underline {\xi })$
should be stronger than the estimate for the codimension of the set
![]() ${\cal B}_*(\underline {\xi })$
by that number. Similarly, P varies in a
${\cal B}_*(\underline {\xi })$
by that number. Similarly, P varies in a
-dimensional family, so that the estimate for the codimension of the set
![]() ${\cal B}_{R3.1}(\underline {\xi },P)$
should be stronger than the estimate for
${\cal B}_{R3.1}(\underline {\xi },P)$
should be stronger than the estimate for
![]() ${\cal B}_{R3.1}(\underline {\xi })$
by that number.
${\cal B}_{R3.1}(\underline {\xi })$
by that number.
Now everything is ready to consider each of the six subsets
![]() ${\cal B}_*$
.
${\cal B}_*$
.
8.2 The conditions (MQ1) and (MQ2)
For a non-singular point
![]() $o\in F$
, these conditions contain no restrictions, so we assume that
$o\in F$
, these conditions contain no restrictions, so we assume that
![]() $\dim \underline {\xi }\leqslant k-1$
. It is well known that the closed subset of quadratic forms of rank
$\dim \underline {\xi }\leqslant k-1$
. It is well known that the closed subset of quadratic forms of rank
![]() $\leqslant r\leqslant N-1$
in the space
$\leqslant r\leqslant N-1$
in the space
![]() ${\cal P}_{2,N}$
has the codimension
${\cal P}_{2,N}$
has the codimension
 $$ \begin{align*}{N-r+1\choose 2}. \end{align*} $$
$$ \begin{align*}{N-r+1\choose 2}. \end{align*} $$
From here, it is easy to see that the closed subset of tuples
![]() $(q_1,\dots ,q_e)=q_{[1,e]}$
of quadratic forms in N variables, defined by the condition
$(q_1,\dots ,q_e)=q_{[1,e]}$
of quadratic forms in N variables, defined by the condition
is of codimension
 $$ \begin{align*}\geqslant{N-r+1\choose 2}-(e-1) \end{align*} $$
$$ \begin{align*}\geqslant{N-r+1\choose 2}-(e-1) \end{align*} $$
in the space
![]() ${\cal P}^{\times e}_{2,N}$
. As we noted in Subsection 1.2 (after stating the condition (MQ2)), for
${\cal P}^{\times e}_{2,N}$
. As we noted in Subsection 1.2 (after stating the condition (MQ2)), for
![]() $l\geqslant 2$
, the condition (MQ2) is stronger than (MQ1); therefore, it is sufficient to estimate the codimension of the set
$l\geqslant 2$
, the condition (MQ2) is stronger than (MQ1); therefore, it is sufficient to estimate the codimension of the set
![]() ${\cal B}_{MQ2}$
(in the case of quadratic points, when
${\cal B}_{MQ2}$
(in the case of quadratic points, when
![]() $l=1$
, it is easy to check that the codimension of the set
$l=1$
, it is easy to check that the codimension of the set
![]() ${\cal B}_{MQ1}$
is higher than required). So we assume that
${\cal B}_{MQ1}$
is higher than required). So we assume that
![]() $\mathop {\mathrm { dim}}\underline {\xi }=k-l\leqslant k-2$
. The condition (MQ2) requires the rank of the tuple of quadratic forms
$\mathop {\mathrm { dim}}\underline {\xi }=k-l\leqslant k-2$
. The condition (MQ2) requires the rank of the tuple of quadratic forms
![]() $q_{[1,k]}$
, where
$q_{[1,k]}$
, where
![]() $q_i=f_{i,2}|_{T_oF}$
, to be at least
$q_i=f_{i,2}|_{T_oF}$
, to be at least
![]() $\rho (k)+2$
; see (1) in Subsection 0.1. Taking into account the variation of the tuple
$\rho (k)+2$
; see (1) in Subsection 0.1. Taking into account the variation of the tuple
![]() $\underline {\xi }$
, from what was said above, it is easy to obtain that the codimension of the set
$\underline {\xi }$
, from what was said above, it is easy to obtain that the codimension of the set
![]() ${\cal B}_{MQ2}\cap {\cal P}^{k-l}(o)\geqslant $
${\cal B}_{MQ2}\cap {\cal P}^{k-l}(o)\geqslant $
 $$ \begin{align*}-k+1+l(M+l)+{M+l-\rho(k)\choose 2}. \end{align*} $$
$$ \begin{align*}-k+1+l(M+l)+{M+l-\rho(k)\choose 2}. \end{align*} $$
The minimum of this expression is attained for
![]() $l=2$
, and it is easy to check that this minimum is precisely
$l=2$
, and it is easy to check that this minimum is precisely
![]() $\gamma +M$
. Therefore, the codimension of the set
$\gamma +M$
. Therefore, the codimension of the set
![]() ${\cal B}_{MQ2}$
is at least
${\cal B}_{MQ2}$
is at least
![]() $\gamma $
, and the codimension of the set
$\gamma $
, and the codimension of the set
![]() ${\cal B}_{MQ1}$
for
${\cal B}_{MQ1}$
for
![]() $l\geqslant 2$
is higher. For
$l\geqslant 2$
is higher. For
![]() $l=1$
, the last codimension is also higher. This completes our consideration of the conditions (MQ1) and (MQ2).
$l=1$
, the last codimension is also higher. This completes our consideration of the conditions (MQ1) and (MQ2).
8.3 Regularity at the non-singular and quadratic points
Let us estimate the codimension of the set
![]() ${\cal B}_{R1}(\underline {\xi },\Pi )$
in the space
${\cal B}_{R1}(\underline {\xi },\Pi )$
in the space
![]() ${\cal P}(o,\underline {\xi })$
. Here,
${\cal P}(o,\underline {\xi })$
. Here,
![]() $\mathop {\mathrm {dim}}\underline {\xi }=k$
and
$\mathop {\mathrm {dim}}\underline {\xi }=k$
and
![]() $\Pi \subset {\mathbb P}(T_oF)$
is a subspace of codimension
$\Pi \subset {\mathbb P}(T_oF)$
is a subspace of codimension
![]() $k+\varepsilon (k)-1=m_*-4$
. Let
$k+\varepsilon (k)-1=m_*-4$
. Let
 $$ \begin{align*}{\cal G}(\underline{d})=\prod^{M-m_*}_{i=1}{\cal P}_{\mathop{\mathrm{ deg}}h_i,\mathop{\mathrm{dim}}\Pi+1} \end{align*} $$
$$ \begin{align*}{\cal G}(\underline{d})=\prod^{M-m_*}_{i=1}{\cal P}_{\mathop{\mathrm{ deg}}h_i,\mathop{\mathrm{dim}}\Pi+1} \end{align*} $$
be the space, parameterizing all sequences
![]() ${\cal S}[-m_*]|_{\Pi }$
. Since the polynomials
${\cal S}[-m_*]|_{\Pi }$
. Since the polynomials
![]() $h_i$
are distinct homogeneous components of the polynomials of the tuple
$h_i$
are distinct homogeneous components of the polynomials of the tuple
![]() $\underline {f}$
, restricted onto the subspace
$\underline {f}$
, restricted onto the subspace
![]() $\Pi $
, the codimension of the subset
$\Pi $
, the codimension of the subset
![]() ${\cal B}_{R1}(\underline {\xi },\Pi )$
in
${\cal B}_{R1}(\underline {\xi },\Pi )$
in
![]() ${\cal P}(o,\underline {\xi })$
is equal to the codimension of the subset
${\cal P}(o,\underline {\xi })$
is equal to the codimension of the subset
![]() ${\cal B}\subset {\cal G}(\underline {d})$
, which consists of the sequences that do not satisfy the condition (R1).
${\cal B}\subset {\cal G}(\underline {d})$
, which consists of the sequences that do not satisfy the condition (R1).
Using the approach that was applied in [Reference Pukhlikov27, Reference Pukhlikov20, Reference Evans and Pukhlikov28] and many other papers, let us present
![]() ${\cal B}$
as a disjoint union
${\cal B}$
as a disjoint union
 $$ \begin{align*}{\cal B}=\bigsqcup^{M-m_*}_{i=1}{\cal B}_i, \end{align*} $$
$$ \begin{align*}{\cal B}=\bigsqcup^{M-m_*}_{i=1}{\cal B}_i, \end{align*} $$
where
![]() ${\cal B}_i$
consists of sequences
${\cal B}_i$
consists of sequences
such that the first
![]() $i-1$
polynomials form a regular sequence but
$i-1$
polynomials form a regular sequence but
![]() $h_i$
vanishes on one of the components of the set of their common zeros. The ‘projection method’ estimates the codimension of
$h_i$
vanishes on one of the components of the set of their common zeros. The ‘projection method’ estimates the codimension of
![]() ${\cal B}_i$
in
${\cal B}_i$
in
![]() ${\cal G}(\underline {d})$
from below by the integer
${\cal G}(\underline {d})$
from below by the integer
 $$ \begin{align} {\mathop{\mathrm{dim}}\Pi-i+1+\mathop{\mathrm{deg}}h_i\choose \mathop{\mathrm{ deg}}h_i} ={\mathop{\mathrm{dim}}\Pi-i+1+\mathop{\mathrm{deg}}h_i\choose \mathop{\mathrm{dim}}\Pi-i+1} \end{align} $$
$$ \begin{align} {\mathop{\mathrm{dim}}\Pi-i+1+\mathop{\mathrm{deg}}h_i\choose \mathop{\mathrm{ deg}}h_i} ={\mathop{\mathrm{dim}}\Pi-i+1+\mathop{\mathrm{deg}}h_i\choose \mathop{\mathrm{dim}}\Pi-i+1} \end{align} $$
(we will use both presentations). It follows easily from here (see [Reference Evans and Pukhlikov28, §3]) that the worst estimate corresponds to the case of equal or ‘almost equal’ degrees
![]() $d_i$
, described above. We will consider this case.
$d_i$
, described above. We will consider this case.
Thus, we need to estimate from below the minimum of
![]() $M-m_*$
integers (23). Here are the first
$M-m_*$
integers (23). Here are the first
![]() $(k+1)$
of them:
$(k+1)$
of them:
 $$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+2\choose 2},\,{\mathop{\mathrm{dim}}\Pi+1\choose 2},\,\dots,\,{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\,{\mathop{\mathrm{ dim}}\Pi+3-k\choose 3}. \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+2\choose 2},\,{\mathop{\mathrm{dim}}\Pi+1\choose 2},\,\dots,\,{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\,{\mathop{\mathrm{ dim}}\Pi+3-k\choose 3}. \end{align*} $$
We call the left-hand side of the equality (23) the presentation of type (I); the right-hand side is the presentation of type (II). Let us write down each of the numbers (23) in the form
 $$ \begin{align*}{A(i)\choose B(i)}, \end{align*} $$
$$ \begin{align*}{A(i)\choose B(i)}, \end{align*} $$
where
![]() $A(i)\geqslant 2B(i)$
, using the presentation of type (I) or of type (II).
$A(i)\geqslant 2B(i)$
, using the presentation of type (I) or of type (II).
At first (for the starting segment of the sequence), we use the presentation of type (I). It is easy to see that when we change i by
![]() $i+1$
, we have one of the two options:
$i+1$
, we have one of the two options:
-
• either
 $\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i$
, and then
$\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i$
, and then
 $A(i+1)=A(i)-1$
and
$A(i+1)=A(i)-1$
and
 $B(i+1)=B(i)$
, so that and moreover,
$B(i+1)=B(i)$
, so that and moreover, $$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}, \end{align*} $$
$$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}, \end{align*} $$
 $C(i)=A(i)-2B(i)$
decreases:
$C(i)=A(i)-2B(i)$
decreases:
 $C(i+1)=C(i)-1$
,
$C(i+1)=C(i)-1$
,
-
• or
 $\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i+1$
, and then
$\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i+1$
, and then
 $A(i+1)=A(i)$
and
$A(i+1)=A(i)$
and
 $B(i+1)=B(i)+1$
, so that
$B(i+1)=B(i)+1$
, so that
 $C(i+1)=C(i)-2$
, and if
$C(i+1)=C(i)-2$
, and if
 $C(i+1)\geqslant 0$
, then
$C(i+1)\geqslant 0$
, then  $$ \begin{align*}{A(i+1)\choose B(i+1)}>{A(i)\choose B(i)}. \end{align*} $$
$$ \begin{align*}{A(i+1)\choose B(i+1)}>{A(i)\choose B(i)}. \end{align*} $$
This is how it goes on until the ‘equilibrium’:
![]() $C(i_*)\geqslant 0$
, but
$C(i_*)\geqslant 0$
, but
![]() $C(i_*+1)<0$
, and after that, we use the presentation of type (II).
$C(i_*+1)<0$
, and after that, we use the presentation of type (II).
Now when we change i by
![]() $(i+1)$
, we have one of the two options:
$(i+1)$
, we have one of the two options:
-
• either
 $\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i$
, and then
$\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i$
, and then
 $A(i+1)=A(i)-1$
and
$A(i+1)=A(i)-1$
and
 $B(i+1)=B(i)-1$
, so that
$B(i+1)=B(i)-1$
, so that
 $C(i+1)=C(i)+1$
and
$C(i+1)=C(i)+1$
and  $$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}, \end{align*} $$
$$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}, \end{align*} $$
-
• or
 $\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i+1$
, and then
$\mathop {\mathrm {deg}}h_{i+1}=\mathop {\mathrm {deg}}h_i+1$
, and then
 $A(i+1)=A(i)$
and
$A(i+1)=A(i)$
and
 $B(i+1)=B(i)-1$
, so that
$B(i+1)=B(i)-1$
, so that
 $C(i+1)=C(i)+2$
and
$C(i+1)=C(i)+2$
and  $$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}. \end{align*} $$
$$ \begin{align*}{A(i+1)\choose B(i+1)}<{A(i)\choose B(i)}. \end{align*} $$
Therefore, after the ‘equilibrium’, our sequence is strictly decreasing. Moreover, if
 $$ \begin{align*}{A(i_1)\choose B(i_1)}\quad\mbox{and}\quad {A(i_2)\choose B(i_2)} \end{align*} $$
$$ \begin{align*}{A(i_1)\choose B(i_1)}\quad\mbox{and}\quad {A(i_2)\choose B(i_2)} \end{align*} $$
are two numbers in our sequence, where
![]() $i_1\leqslant i_*$
and
$i_1\leqslant i_*$
and
![]() $i_2>i_*$
and
$i_2>i_*$
and
![]() $B(i_1)\geqslant B(i_2)$
, then, obviously,
$B(i_1)\geqslant B(i_2)$
, then, obviously,
 $$ \begin{align*}{A(i_1)\choose B(i_1)}>{A(i_2)\choose B(i_2)}. \end{align*} $$
$$ \begin{align*}{A(i_1)\choose B(i_1)}>{A(i_2)\choose B(i_2)}. \end{align*} $$
Recall that the degrees
![]() $d_i$
are equal or ‘almost equal’.
$d_i$
are equal or ‘almost equal’.
Lemma 8.1. For
![]() $M\geqslant 3k^2$
, the following inequality holds:
$M\geqslant 3k^2$
, the following inequality holds:
![]() $i_*<M-m_*$
.
$i_*<M-m_*$
.
Proof. Elementary computations, using the equality
![]() $C(i+k)=C(i)-(k+1)$
if
$C(i+k)=C(i)-(k+1)$
if
![]() $C(i+k)\geqslant 0$
. Q.E.D. for the lemma.
$C(i+k)\geqslant 0$
. Q.E.D. for the lemma.
Therefore, the ‘equilibrium’ is reached earlier than the sequence
![]() $h_i,\dots ,h_{M-m_*}$
comes to an end, so that there is a nonempty segment after the ‘equilibrium’. By construction,
$h_i,\dots ,h_{M-m_*}$
comes to an end, so that there is a nonempty segment after the ‘equilibrium’. By construction,
![]() $B(M-m_*)=4$
. By what was said above, the minimum of the numbers
$B(M-m_*)=4$
. By what was said above, the minimum of the numbers
![]() ${A(i)\choose B(i)}$
for
${A(i)\choose B(i)}$
for
![]() $i=1,\dots ,M-m_*$
is the minimum of the following three numbers:
$i=1,\dots ,M-m_*$
is the minimum of the following three numbers:
 $$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\quad {\mathop{\mathrm{ dim}}\Pi+4-2k\choose 3},\quad {\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}. \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\quad {\mathop{\mathrm{ dim}}\Pi+4-2k\choose 3},\quad {\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}. \end{align*} $$
Lemma 8.2. For
![]() $\mathop {\mathrm {dim}}\Pi \geqslant 3k+1$
, the following inequality holds:
$\mathop {\mathrm {dim}}\Pi \geqslant 3k+1$
, the following inequality holds:
 $$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+4-2k\choose 3}>{\mathop{\mathrm{ dim}}\Pi+3-k\choose 2}. \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+4-2k\choose 3}>{\mathop{\mathrm{ dim}}\Pi+3-k\choose 2}. \end{align*} $$
Proof. Elementary computations. Q.E.D.
Lemma 8.3. For
![]() $M\geqslant 2\sqrt {3}k^2$
, the following inequality holds:
$M\geqslant 2\sqrt {3}k^2$
, the following inequality holds:
 $$ \begin{align*}{\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}>{\mathop{\mathrm{ dim}}\Pi+3-k\choose 2}. \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}>{\mathop{\mathrm{ dim}}\Pi+3-k\choose 2}. \end{align*} $$
Proof. It is easy to check the inequalities
 $$ \begin{align*}\frac{(M-2k)^2}{2}\geqslant{\mathop{\mathrm{dim}}\Pi+3-k\choose 2} \end{align*} $$
$$ \begin{align*}\frac{(M-2k)^2}{2}\geqslant{\mathop{\mathrm{dim}}\Pi+3-k\choose 2} \end{align*} $$
and
 $$ \begin{align*}{\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}\geqslant\frac{1}{24} \left(\frac{M}{k}+1\right)\left(\frac{M}{k}\right)\left(\frac{M}{k}-1\right) \left(\frac{M}{k}-2\right), \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{deg}}h_{M-m_*}+4\choose 4}\geqslant\frac{1}{24} \left(\frac{M}{k}+1\right)\left(\frac{M}{k}\right)\left(\frac{M}{k}-1\right) \left(\frac{M}{k}-2\right), \end{align*} $$
so that it is sufficient to show that for
![]() $M\geqslant 2\sqrt {3}k^2$
, the inequality
$M\geqslant 2\sqrt {3}k^2$
, the inequality
 $$ \begin{align*}\left(\frac{M^2}{k^2}-1\right)\left(\frac{M^2}{k^2}-2\frac{M}{k}\right)>12(M-2k)^2 \end{align*} $$
$$ \begin{align*}\left(\frac{M^2}{k^2}-1\right)\left(\frac{M^2}{k^2}-2\frac{M}{k}\right)>12(M-2k)^2 \end{align*} $$
holds or, equivalently,
![]() $M(M^2-k^2)>12k^4(M-2k)$
. It is easy to check the last inequality, considering the cubic polynomial
$M(M^2-k^2)>12k^4(M-2k)$
. It is easy to check the last inequality, considering the cubic polynomial
in the real variable t. Q.E.D. for the lemma.
The work that was carried out above gives the inequality
 $$ \begin{align*}\mathop{\mathrm{codim}}({\cal B}\subset{\cal G}(\underline{d}))\geqslant{M+3-2k-\varepsilon(k)\choose 2}. \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{codim}}({\cal B}\subset{\cal G}(\underline{d}))\geqslant{M+3-2k-\varepsilon(k)\choose 2}. \end{align*} $$
From here, by elementary computations (taking into account the variation of the subspace
![]() $\Pi $
, see Subsection 8.1), it is easy to obtain the required inequality
$\Pi $
, see Subsection 8.1), it is easy to obtain the required inequality
![]() $\mathop {\mathrm {codim}}({\cal B}_{R1}\subset {\cal P}(o))\geqslant \gamma +M$
. This completes the proof in the case of smooth points.
$\mathop {\mathrm {codim}}({\cal B}_{R1}\subset {\cal P}(o))\geqslant \gamma +M$
. This completes the proof in the case of smooth points.
It is easy to see that the methods used above give a stronger estimate for the codimension of the set
![]() ${\cal B}_{R2}$
because the dimension of the subspace
${\cal B}_{R2}$
because the dimension of the subspace
![]() $\Pi $
is higher. The computations are completely similar to the computations given above for the case of a non-singular point. For that reason, we do not consider the case of a quadratic point, and we move on to estimating the codimension of the sets
$\Pi $
is higher. The computations are completely similar to the computations given above for the case of a non-singular point. For that reason, we do not consider the case of a quadratic point, and we move on to estimating the codimension of the sets
![]() ${\cal B}_{R3.1}$
and
${\cal B}_{R3.1}$
and
![]() ${\cal B}_{R3.2}$
.
${\cal B}_{R3.2}$
.
8.4 Regularity at the multi-quadratic points
Let us estimate the codimension of the set
![]() ${\cal B}_{R3.2}(\underline {\xi },\Pi )$
, where
${\cal B}_{R3.2}(\underline {\xi },\Pi )$
, where
![]() $\Pi \subset {\mathbb P}(T_oF)$
is an arbitrary subspace of codimension
$\Pi \subset {\mathbb P}(T_oF)$
is an arbitrary subspace of codimension
![]() $\varepsilon (k)$
. Our arguments are completely similar to the arguments of Subsection 8.3 for a non-singular point and give a stronger estimate for the codimension. We just point out the necessary changes in the constructions of Subsection 8.3. Set
$\varepsilon (k)$
. Our arguments are completely similar to the arguments of Subsection 8.3 for a non-singular point and give a stronger estimate for the codimension. We just point out the necessary changes in the constructions of Subsection 8.3. Set
 $$ \begin{align*}{\cal G}(\underline{d})=\prod^{M-m^*}_{i=1}{\cal P}_{\mathop{\mathrm{ deg}} h_i,\mathop{\mathrm{dim}}\Pi+1}. \end{align*} $$
$$ \begin{align*}{\cal G}(\underline{d})=\prod^{M-m^*}_{i=1}{\cal P}_{\mathop{\mathrm{ deg}} h_i,\mathop{\mathrm{dim}}\Pi+1}. \end{align*} $$
Denote by the symbol
![]() ${\cal B}$
the subset in
${\cal B}$
the subset in
![]() ${\cal G}(\underline {d})$
, consisting of the sequences that do not satisfy the condition (R3.2). Again, we break
${\cal G}(\underline {d})$
, consisting of the sequences that do not satisfy the condition (R3.2). Again, we break
![]() ${\cal B}$
into subsets:
${\cal B}$
into subsets:
 $$ \begin{align*}{\cal B}=\bigsqcup^{M-m^*}_{i=1}{\cal B}_i, \end{align*} $$
$$ \begin{align*}{\cal B}=\bigsqcup^{M-m^*}_{i=1}{\cal B}_i, \end{align*} $$
where
![]() ${\cal B}_i$
has the same meaning as in Subsection 8.3 (but for the multi-quadratic point o). Again, the codimension of
${\cal B}_i$
has the same meaning as in Subsection 8.3 (but for the multi-quadratic point o). Again, the codimension of
![]() ${\cal B}_i$
in
${\cal B}_i$
in
![]() ${\cal G}(\underline {d})$
is bounded from below by the number (23), and for k and M fixed, the worst estimate corresponds to the case of equal or ‘almost equal’ degrees
${\cal G}(\underline {d})$
is bounded from below by the number (23), and for k and M fixed, the worst estimate corresponds to the case of equal or ‘almost equal’ degrees
![]() $d_i$
.
$d_i$
.
Arguing precisely in the same way as in the non-singular case (Subsection 8.3), we see, since the dimension of the subspace
![]() $\Pi $
is higher than in the non-singular case, that the claim of Lemma 8.1 is true. Note that if
$\Pi $
is higher than in the non-singular case, that the claim of Lemma 8.1 is true. Note that if
![]() $m^*=0$
, then in the notations of Subsection 8.3, we have
$m^*=0$
, then in the notations of Subsection 8.3, we have
![]() $B(M-m^*)\geqslant 4$
. Thus, replacing
$B(M-m^*)\geqslant 4$
. Thus, replacing
![]() $B(M-m^*)$
by 4, we get that
$B(M-m^*)$
by 4, we get that
![]() $\mathop {\mathrm {codim}}({\cal B}\subset {\cal G}(\underline {d}))$
is bounded from below by the least of the three numbers
$\mathop {\mathrm {codim}}({\cal B}\subset {\cal G}(\underline {d}))$
is bounded from below by the least of the three numbers
 $$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\quad {\mathop{\mathrm{ dim}}\Pi+4-2k\choose 3},\quad {\mathop{\mathrm{deg}}h_{M-m^*}+4\choose 4}. \end{align*} $$
$$ \begin{align*}{\mathop{\mathrm{dim}}\Pi+3-k\choose 2},\quad {\mathop{\mathrm{ dim}}\Pi+4-2k\choose 3},\quad {\mathop{\mathrm{deg}}h_{M-m^*}+4\choose 4}. \end{align*} $$
The claim of Lemma 8.2 is true since, as we noted above,
![]() $\mathop {\mathrm {dim}} \Pi $
in the multi-quadratic case is higher than in the non-singular case. Obviously,
$\mathop {\mathrm {dim}} \Pi $
in the multi-quadratic case is higher than in the non-singular case. Obviously,
![]() $m^*<m_*$
, so that
$m^*<m_*$
, so that
![]() $\mathop {\mathrm {deg}} h_{M-m^*}\geqslant \mathop {\mathrm {deg}}h_{M-m_*}$
, and the claim of Lemma 8.3 is also true. As a result, we get the inequality
$\mathop {\mathrm {deg}} h_{M-m^*}\geqslant \mathop {\mathrm {deg}}h_{M-m_*}$
, and the claim of Lemma 8.3 is also true. As a result, we get the inequality
 $$ \begin{align*}\mathop{\mathrm{codim}}({\cal B}\subset{\cal G}(\underline{d}))\geqslant{M+2+l-k-\varepsilon(k)\choose 2}, \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{codim}}({\cal B}\subset{\cal G}(\underline{d}))\geqslant{M+2+l-k-\varepsilon(k)\choose 2}, \end{align*} $$
where
![]() $\mathop {\mathrm {dim}}\underline {\xi }=k-l$
. The minimum of the right-hand side is attained for
$\mathop {\mathrm {dim}}\underline {\xi }=k-l$
. The minimum of the right-hand side is attained for
![]() $l=2$
, and it is easy to see that this minimum is significantly higher than in the non-singular case. It is easy to check, taking into account the variation of the subspace
$l=2$
, and it is easy to see that this minimum is significantly higher than in the non-singular case. It is easy to check, taking into account the variation of the subspace
![]() $\Pi $
, that
$\Pi $
, that
This completes our consideration of the condition (R3.2) in the multi-quadratic case.
8.5 The condition (R3.1)
In order to estimate the codimension of the set
![]() ${\cal B}_{R3.1}(\underline {\xi },P)$
, we need the following known general fact. Take
${\cal B}_{R3.1}(\underline {\xi },P)$
, we need the following known general fact. Take
![]() $e\geqslant 1$
and let
$e\geqslant 1$
and let
![]() $\underline {w}=(w_1,\dots ,w_e)\in {\mathbb Z}^e$
be a tuple of integers, where
$\underline {w}=(w_1,\dots ,w_e)\in {\mathbb Z}^e$
be a tuple of integers, where
![]() $2\leqslant w_1\leqslant \dots \leqslant w_e$
.
$2\leqslant w_1\leqslant \dots \leqslant w_e$
.
Set
 $$ \begin{align*}{\cal P}(\underline{w})=\prod^e_{i=1}{\cal P}_{w_i,N+1} \end{align*} $$
$$ \begin{align*}{\cal P}(\underline{w})=\prod^e_{i=1}{\cal P}_{w_i,N+1} \end{align*} $$
to be the space of tuples
![]() $\underline {g}=(g_1,\dots ,g_e)$
of homogeneous polynomials in
$\underline {g}=(g_1,\dots ,g_e)$
of homogeneous polynomials in
![]() $N+1$
variables,
$N+1$
variables,
![]() $\mathop{\mathrm { deg}}g_i=w_i$
, which we consider as homogeneous polynomials on
$\mathop{\mathrm { deg}}g_i=w_i$
, which we consider as homogeneous polynomials on
![]() ${\mathbb P}^N$
. Let
${\mathbb P}^N$
. Let
be the set of tuples
![]() $\underline {g}$
, such that the scheme of their common zeros is not an irreducible reduced subvariety of codimension e in
$\underline {g}$
, such that the scheme of their common zeros is not an irreducible reduced subvariety of codimension e in
![]() ${\mathbb P}^N$
.
${\mathbb P}^N$
.
Theorem 8.1. The following inequality holds:
Proof. This is Theorem 2.1 in [Reference Pukhlikov2].
Let us estimate the codimension of the set
![]() ${\cal B}_{R3.1}(\underline {\xi },\Pi )$
. In order to do this, consider in the projective space P a hypersurface
${\cal B}_{R3.1}(\underline {\xi },\Pi )$
. In order to do this, consider in the projective space P a hypersurface
![]() $P^{\sharp }$
that does not contain the point o – for instance, the intersection of the hyperplane ‘at infinity’ with respect to the system of affine coordinates
$P^{\sharp }$
that does not contain the point o – for instance, the intersection of the hyperplane ‘at infinity’ with respect to the system of affine coordinates
![]() $(z_1,\dots ,z_{M+k})$
with the subspace P. If the scheme of common zeros of the tuple of polynomials, consisting of
$(z_1,\dots ,z_{M+k})$
with the subspace P. If the scheme of common zeros of the tuple of polynomials, consisting of
and the polynomials
![]() $f_{i,2}|_P$
for i such that
$f_{i,2}|_P$
for i such that
![]() $d_i\geqslant 3$
is not an irreducible reduced subvariety of codimension
$d_i\geqslant 3$
is not an irreducible reduced subvariety of codimension
![]() $k+k_{\geqslant 3}$
in P (that is, the condition (R3.1) is violated; see Subsection 1.4), then the scheme of common zeros of the set of polynomials
$k+k_{\geqslant 3}$
in P (that is, the condition (R3.1) is violated; see Subsection 1.4), then the scheme of common zeros of the set of polynomials
respectively, is reducible, non-reduced or of codimension
![]() $<k+k_{\geqslant 3}$
in
$<k+k_{\geqslant 3}$
in
![]() $P^{\sharp }$
. However, for each i, such that
$P^{\sharp }$
. However, for each i, such that
![]() $d_i\geqslant 3$
, the homogeneous polynomials
$d_i\geqslant 3$
, the homogeneous polynomials
on the projective space
![]() $P^{\sharp }$
are linear combinations of disjoint sets of monomials in
$P^{\sharp }$
are linear combinations of disjoint sets of monomials in
![]() $f_i$
, so that the coefficients of those polynomials belong to disjoint subsets of coefficients of the polynomial
$f_i$
, so that the coefficients of those polynomials belong to disjoint subsets of coefficients of the polynomial
![]() $f_i$
. Therefore (re-ordering the polynomials of the tuple (24) so that their degrees do not decrease), applying Theorem 8.1 to the tuple (24), we get that the codimension of the set
$f_i$
. Therefore (re-ordering the polynomials of the tuple (24) so that their degrees do not decrease), applying Theorem 8.1 to the tuple (24), we get that the codimension of the set
![]() ${\cal B}_{R3.1}(\underline {\xi },P)$
is at least
${\cal B}_{R3.1}(\underline {\xi },P)$
is at least
where
![]() $\mathop {\mathrm {dim}}P^{\sharp }=M+l-\varepsilon (k)-1$
,
$\mathop {\mathrm {dim}}P^{\sharp }=M+l-\varepsilon (k)-1$
,
![]() $\mathop {\mathrm {dim}}\underline {\xi }=k-l$
. It is easy to check by elementary computations that this estimate (with the correction due to the variation of the subspace P and the set of linear forms
$\mathop {\mathrm {dim}}\underline {\xi }=k-l$
. It is easy to check by elementary computations that this estimate (with the correction due to the variation of the subspace P and the set of linear forms
![]() $\underline {\xi }$
) is stronger than we need.
$\underline {\xi }$
) is stronger than we need.
This completes the proof of the estimate for the codimension of the complement
![]() ${\cal P}\backslash {\cal F}$
in Theorem 0.1.
${\cal P}\backslash {\cal F}$
in Theorem 0.1.
Note that (for the technique of estimating the codimension that we used) the estimate of Theorem 0.1 is optimal for the condition (MQ2); that requirement turns out to be the strongest.
Competing interest
The authors have no competing interest to declare.